Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритмы на графах Графы. Основные определения
Содержание
- 1. Алгоритмы на графах Графы. Основные определения
- 2. 17.03.2014Алгоритмы на графах Начало1. Графы.
- 3. 17.03.2014Алгоритмы на графах НачалоОриентированный граф
- 4. 17.03.2014Алгоритмы на графах НачалоГрафы. Основные
- 5. 17.03.2014Алгоритмы на графах НачалоСтепень вершины
- 6. 17.03.2014Алгоритмы на графах НачалоГрафы. Основные
- 7. 17.03.2014Алгоритмы на графах НачалоДругое определение
- 8. 17.03.2014Алгоритмы на графах Начало ba1F−1
- 9. 17.03.2014Алгоритмы на графах НачалоДругое определение
- 10. 17.03.2014Алгоритмы на графах НачалоΓ−1 −
- 11. 17.03.2014Алгоритмы на графах НачалоУпорядоченный графG
- 12. 17.03.2014Алгоритмы на графах НачалоУпорядоченный графУпорядоченные
- 13. 17.03.2014Алгоритмы на графах НачалоУпорядоченный графГрафы.
- 14. 17.03.2014Алгоритмы на графах НачалоМатрица инциденций
- 15. 17.03.2014Алгоритмы на графах НачалоМатрица инциденций
- 16. 17.03.2014Алгоритмы на графах НачалоA[u, v]
- 17. 17.03.2014Алгоритмы на графах НачалоДля неориентированного
- 18. 17.03.2014Алгоритмы на графах НачалоСписки смежности
- 19. 17.03.2014Алгоритмы на графах НачалоСписки смежностиРеализация
- 20. 17.03.2014Алгоритмы на графах НачалоСписки смежностиfor
- 21. 17.03.2014Алгоритмы на графах НачалоЗадание: Написать
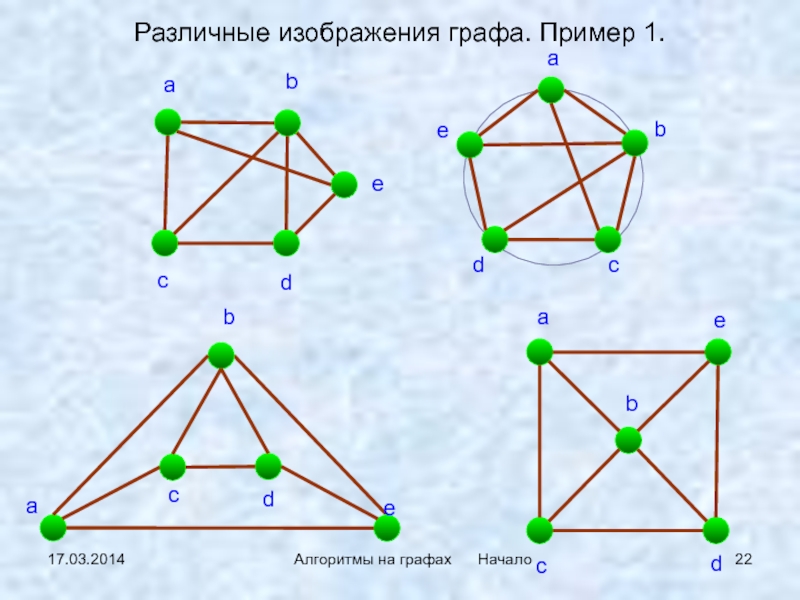
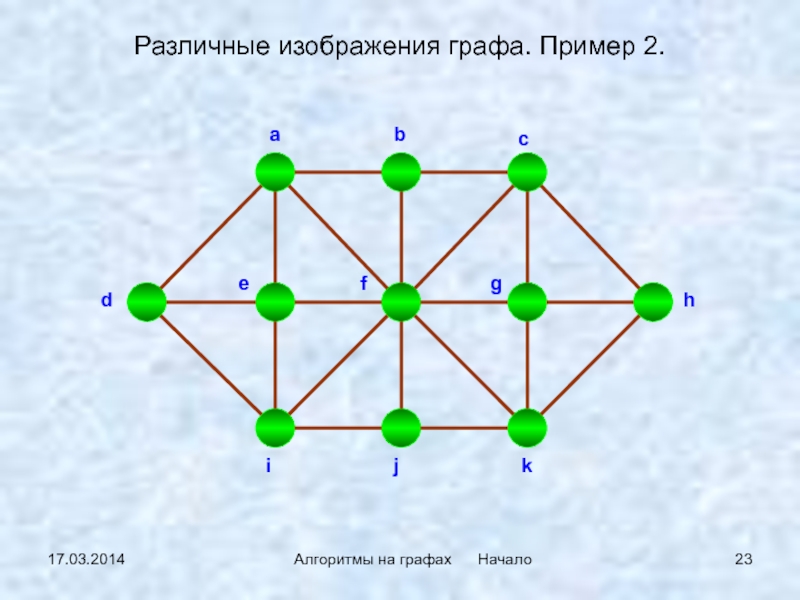
- 22. 17.03.2014Алгоритмы на графах НачалоРазличные изображения графа. Пример 1.
- 23. 17.03.2014Алгоритмы на графах НачалоРазличные изображения графа. Пример 2.
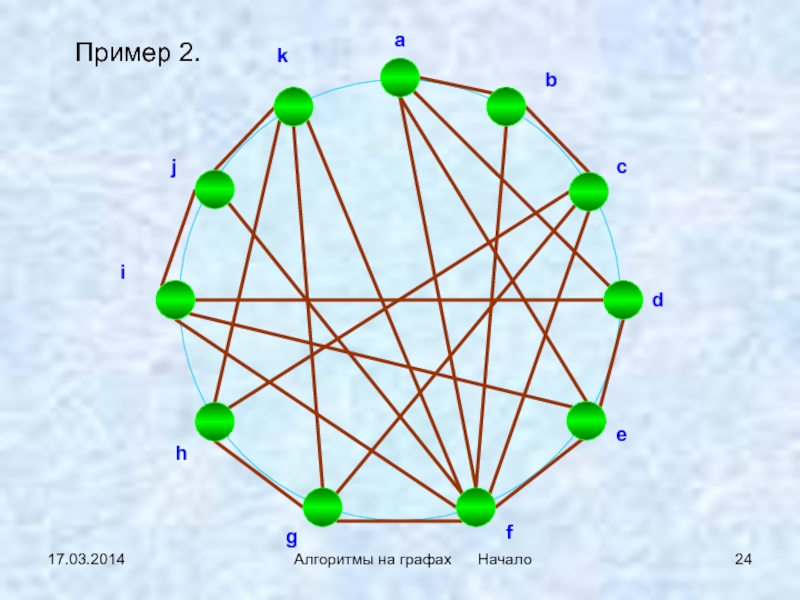
- 24. 17.03.2014Алгоритмы на графах НачалоПример 2.
- 25. 17.03.2014Алгоритмы на графах НачалоМножества вершин
- 26. 17.03.2014Алгоритмы на графах НачалоМножества смежностиΓ(a)={b,c,e}Γ(b)={a,c,d,e}Γ(c)={a,b,d}Γ(d)={b,c,e}Γ(e)={a,b,d}
- 27. 17.03.2014Алгоритмы на графах НачалоСписки смежностиL(a)=(b,c,e)L(b)=(a,c,d,e)L(c)=(a,b,d)L(d)=(b,c,e)L(e)=(a,b,d)
- 28. 17.03.2014Алгоритмы на графах НачалоКонец вводной части
- 29. 17.03.2014Алгоритмы на графах НачалоДерево –
- 30. 17.03.2014Алгоритмы на графах НачалоОстовные деревья
- 31. 17.03.2014Алгоритмы на графах НачалоПример: решетчатый графКартинка из «Седжвик, ч.1-4»
- 32. 17.03.2014Алгоритмы на графах НачалоРассмотрим простой
- 33. 17.03.2014Алгоритмы на графах НачалоПример графа
- 34. 17.03.2014Алгоритмы на графах НачалоПримерИдея: пусть
- 35. 17.03.2014Алгоритмы на графах НачалоАлгоритмfor (i
- 36. 17.03.2014Алгоритмы на графах НачалоПример работы
- 37. 17.03.2014Алгоритмы на графах НачалоТот же графПри другом порядке предъявления ребер:{1,2,4} {3,6} {5,7,8,9}
- 38. 17.03.2014Алгоритмы на графах НачалоРеализация:
- 39. int i, j, k, p, q, w[N];
- 40. 1 21 4 3 6 5 8
- 41. 17.03.2014Алгоритмы на графах НачалоПример
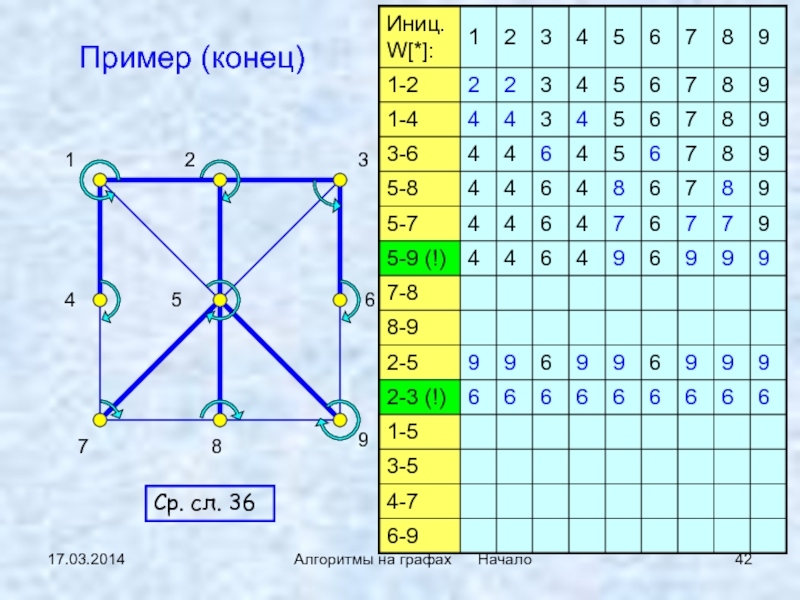
- 42. 17.03.2014Алгоритмы на графах НачалоПример (конец)Ср. сл. 36
- 43. 1 21 4 3 6 5 8
- 44. Реализация: не очень быстрый поиск –
- 45. 17.03.2014Алгоритмы на графах Начало{1,2,4} {3,6}
- 46. 17.03.2014Алгоритмы на графах НачалоПример
- 47. 1 21 4 3 6 5 8
- 48. 1 21 4 3 6 5 8
- 49. 17.03.2014Алгоритмы на графах Начало
- 50. 17.03.2014Алгоритмы на графах НачалоГраф G
- 51. 17.03.2014Алгоритмы на графах НачалоПродолжение задачи «Построение МОД»на следующей лекции
- 52. 17.03.2014Алгоритмы на графах НачалоКОНЕЦ
- 53. Скачать презентанцию
Слайды и текст этой презентации
Слайд 217.03.2014
Алгоритмы на графах Начало
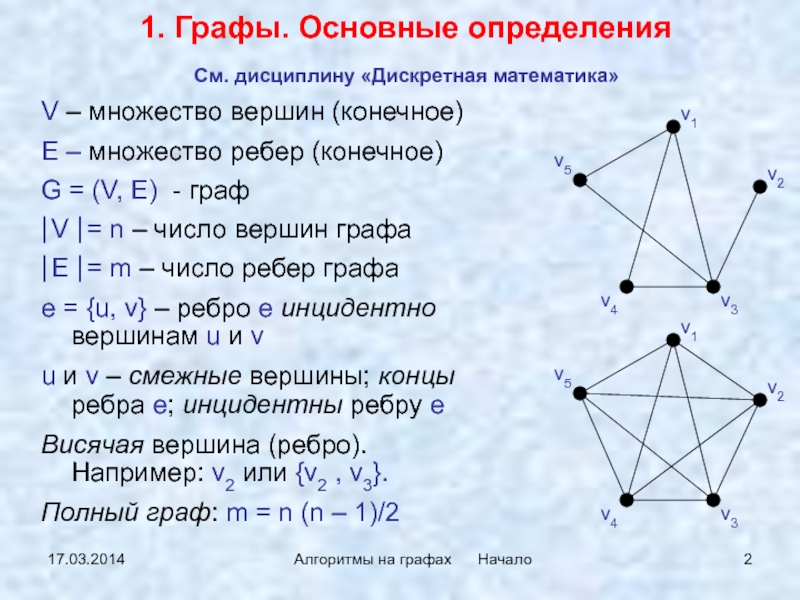
1. Графы. Основные определения
V –
множество вершин (конечное)
E – множество ребер (конечное)
G = (V, E)
- граф⎢V ⎢= n – число вершин графа
⎢E ⎢= m – число ребер графа
e = {u, v} – ребро e инцидентно вершинам u и v
u и v – смежные вершины; концы ребра e; инцидентны ребру e
Висячая вершина (ребро). Например: v2 или {v2 , v3}.
Полный граф: m = n (n – 1)/2
См. дисциплину «Дискретная математика»
Слайд 317.03.2014
Алгоритмы на графах Начало
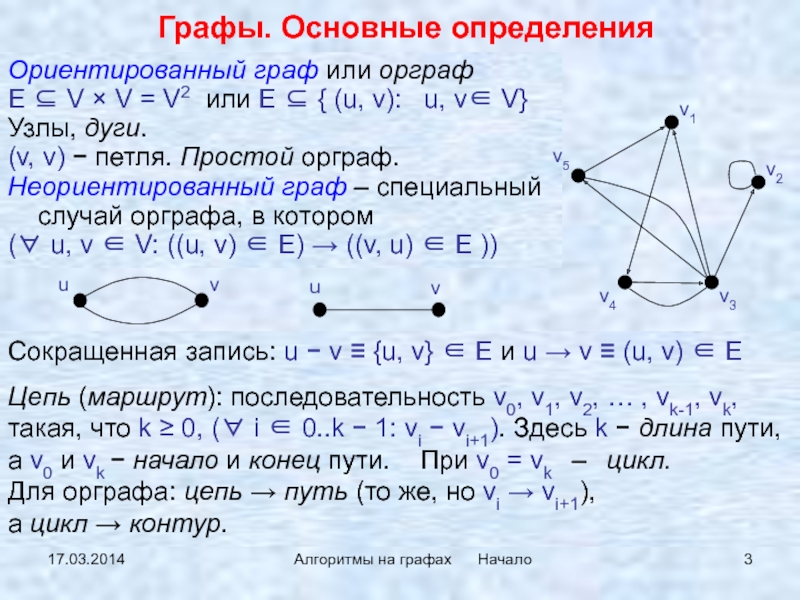
Ориентированный граф или орграф
E ⊆
V × V = V2 или E ⊆ { (u,
v): u, v∈ V}Узлы, дуги.
(v, v) − петля. Простой орграф.
Неориентированный граф – специальный случай орграфа, в котором
(∀ u, v ∈ V: ((u, v) ∈ E) → ((v, u) ∈ E ))
Графы. Основные определения
Сокращенная запись: u − v ≡ {u, v} ∈ E и u → v ≡ (u, v) ∈ E
Цепь (маршрут): последовательность v0, v1, v2, … , vk-1, vk, такая, что k ≥ 0, (∀ i ∈ 0..k − 1: vi − vi+1). Здесь k − длина пути, а v0 и vk − начало и конец пути. При v0 = vk – цикл. Для орграфа: цепь → путь (то же, но vi → vi+1), а цикл → контур.
Слайд 417.03.2014
Алгоритмы на графах Начало
Графы. Основные определения
Аналогично для графа
(неориентированного графа)
E ⊆ { {u, v}: (u, v∈ V)
& (u ≠ v)} или более строго:
Iv = { (v, v): v∈ V}, V2 = V × V = { (u, v): u, v∈ V}, V−2 = V2 \ Iv ;
отношение эквивалентности на множестве V−2 :
(u, v) ~ (s, t), если либо (u, v) = (s, t), либо (u, v) = (t, s);
множество классов эквивалентности (фактор-множество) V−2/ ~ ;
в каждом классе ровно два элемента { (u, v), (v, u)}.
Тогда для графа E ⊆ V−2/ ~
Слайд 517.03.2014
Алгоритмы на графах Начало
Степень вершины d(v) – число
инцидентных ей ребер (дуг).
Для орграфа:
dout(v) - полустепень исхода, din(v) -
полустепень захода.d(v) = dout(v) + din(v)
Для изолированной вершины: d(v) = 0.
Для висячей вершины: d(v) = 1.
Графы. Основные определения
Слайд 617.03.2014
Алгоритмы на графах Начало
Графы. Основные определения
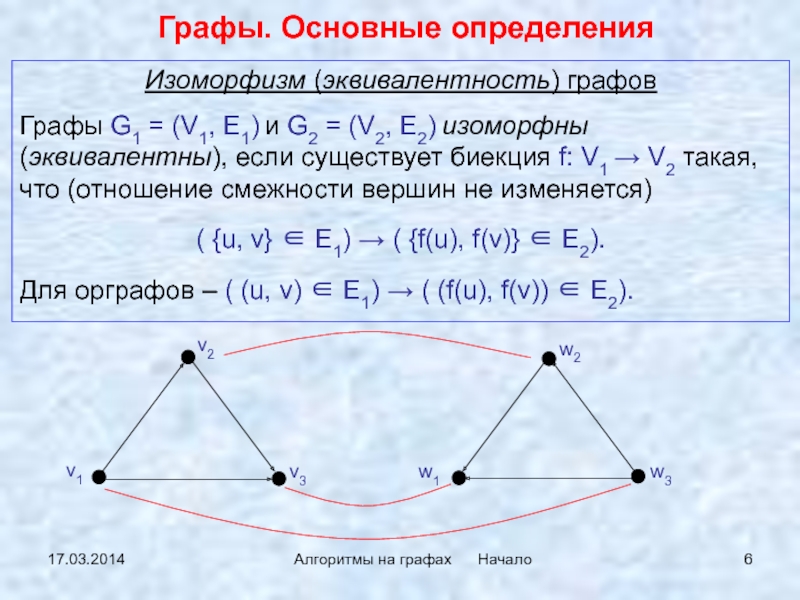
Изоморфизм (эквивалентность) графов
Графы
G1 = (V1, E1) и G2 = (V2, E2) изоморфны
(эквивалентны), если существует биекция f: V1 → V2 такая, что (отношение смежности вершин не изменяется)( {u, v} ∈ E1) → ( {f(u), f(v)} ∈ E2).
Для орграфов – ( (u, v) ∈ E1) → ( (f(u), f(v)) ∈ E2).
Слайд 717.03.2014
Алгоритмы на графах Начало
Другое определение графа (орграфа)
Отступление. Соответствие
Графы
и бинарные отношения.
Бинарное отношение: R ⊆ A × B. Вместо
(a, b) ∈ R пишут aRb. При A = B , говорят, что R – отношение на A.
Про бинарное отношение R ⊆ A × B часто говорят как про соответствие с областью отправления A и областью прибытия B или соответствие на A × B.
Записывают, как F: A → B и b = F(a).
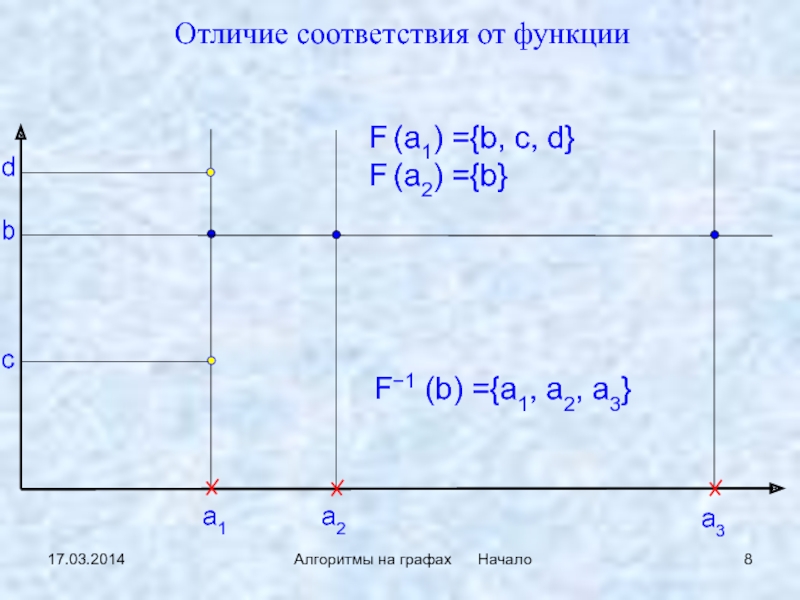
Полный образ элемента x ∈ A :
F(x) = {y ∈ B : y = F(x)}
Полный прообраз элемента y ∈ B :
F−1(y) = {x ∈ A : y = F(x)}
Графы. Основные определения
Слайд 817.03.2014
Алгоритмы на графах Начало
b
a1
F−1 (b) ={a1, a2,
a3}
a2
a3
F (a1) ={b, c, d}
F (a2) ={b}
c
d
Отличие соответствия от функции
Слайд 917.03.2014
Алгоритмы на графах Начало
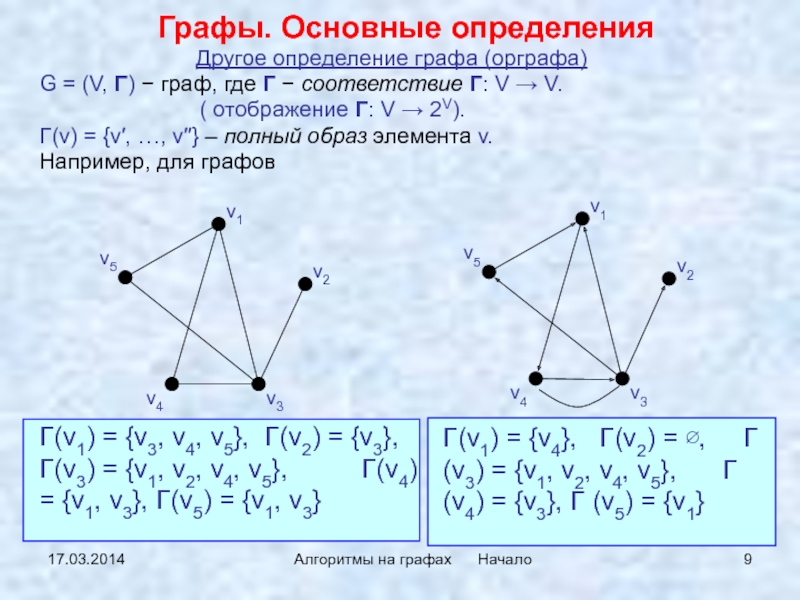
Другое определение графа (орграфа)
G =
(V, Γ) − граф, где Γ − соответствие Γ: V
→ V.( отображение Γ: V → 2V).
Γ(v) = {v′, …, v′′} – полный образ элемента v.
Например, для графов
Графы. Основные определения
Γ(v1) = {v3, v4, v5}, Γ(v2) = {v3}, Γ(v3) = {v1, v2, v4, v5}, Γ(v4) = {v1, v3}, Γ(v5) = {v1, v3}
Γ(v1) = {v4}, Γ(v2) = ∅, Γ (v3) = {v1, v2, v4, v5}, Γ (v4) = {v3}, Γ (v5) = {v1}
Слайд 1017.03.2014
Алгоритмы на графах Начало
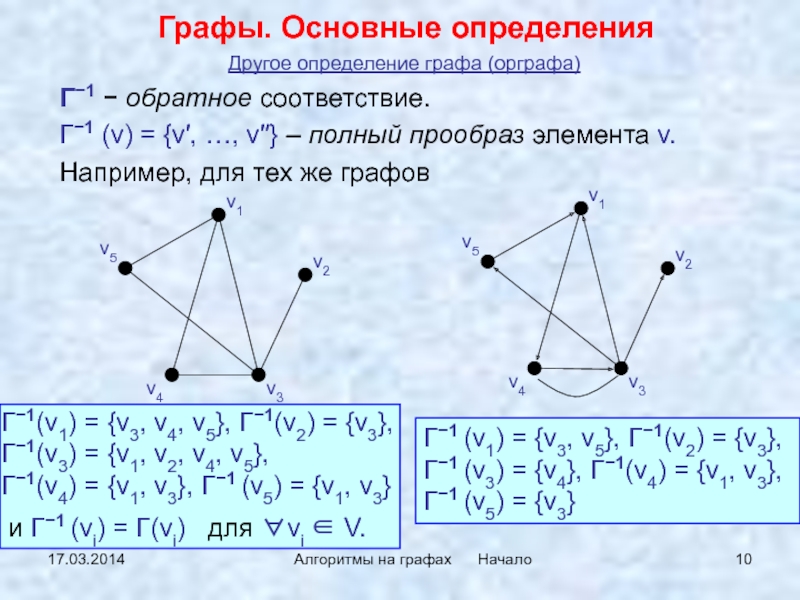
Γ−1 − обратное соответствие.
Γ−1 (v)
= {v′, …, v′′} – полный прообраз элемента v.
Например, для
тех же графовГрафы. Основные определения
Другое определение графа (орграфа)
Γ−1(v1) = {v3, v4, v5}, Γ−1(v2) = {v3}, Γ−1(v3) = {v1, v2, v4, v5}, Γ−1(v4) = {v1, v3}, Γ−1 (v5) = {v1, v3}
и Γ−1 (vi) = Γ(vi) для ∀vi ∈ V.
Γ−1 (v1) = {v3, v5}, Γ−1(v2) = {v3}, Γ−1 (v3) = {v4}, Γ−1(v4) = {v1, v3}, Γ−1 (v5) = {v3}
Слайд 1117.03.2014
Алгоритмы на графах Начало
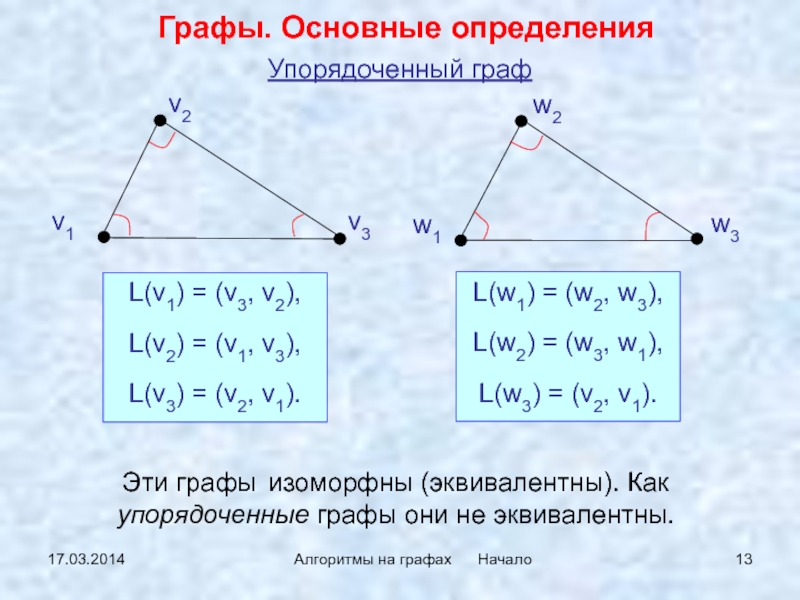
Упорядоченный граф
G = (V, L)
− упорядоченный граф, где L – множество упорядоченных списков вершин
L = {L(v1), L(v2), …, L(vn)}
и L(v) = (v′, …, v′′) – упорядоченный список вершин, смежных с v, т.е. упорядоченный полный образ v. При этом должны выполняться условия
А) v ∉ L(v) для любого v ∈ V,
Б) w ∈ L(v) → v ∈ L(w)
Упорядоченный граф определяет единственный неупорядоченный граф. Обратное неверно, поскольку возможно много способов упорядочения графа.
Графы. Основные определения
Слайд 1217.03.2014
Алгоритмы на графах Начало
Упорядоченный граф
Упорядоченные графы G1 =
(V1, L 1) и G2 = (V2, L 2) изоморфны
(эквивалентны),если существует биекция f: V1 → V2 такая,
что (списковая структура сохраняется),
если список смежных вершин в G1 есть
L(v) = (w′, …, w′′),
то список смежных вершин в G2 есть
L(f(v)) = (f(w′), …, f(w′′)).
Графы. Основные определения
Слайд 1317.03.2014
Алгоритмы на графах Начало
Упорядоченный граф
Графы. Основные определения
v1
v2
v3
w1
w2
w3
Эти графы
изоморфны (эквивалентны). Как упорядоченные графы они не эквивалентны.
L(v1) = (v3,
v2), L(v2) = (v1, v3),
L(v3) = (v2, v1).
L(w1) = (w2, w3),
L(w2) = (w3, w1),
L(w3) = (v2, v1).
Слайд 1417.03.2014
Алгоритмы на графах Начало
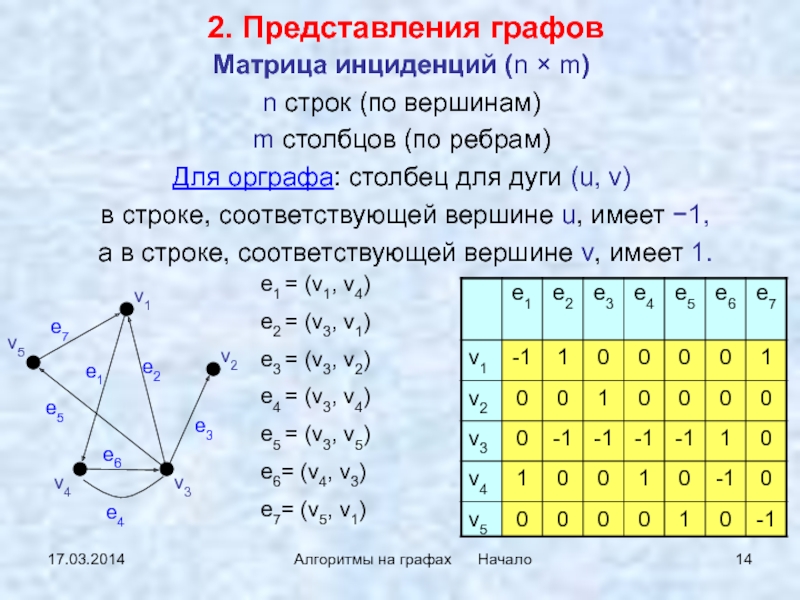
Матрица инциденций (n × m)
n
строк (по вершинам)
m столбцов (по ребрам)
Для орграфа: столбец для дуги
(u, v)в строке, соответствующей вершине u, имеет −1,
а в строке, соответствующей вершине v, имеет 1.
2. Представления графов
e1 = (v1, v4)
e2 = (v3, v1)
e3 = (v3, v2)
e4 = (v3, v4)
e5 = (v3, v5)
e6= (v4, v3)
e7= (v5, v1)
e1
e2
e3
e4
e6
e5
e7
Слайд 1517.03.2014
Алгоритмы на графах Начало
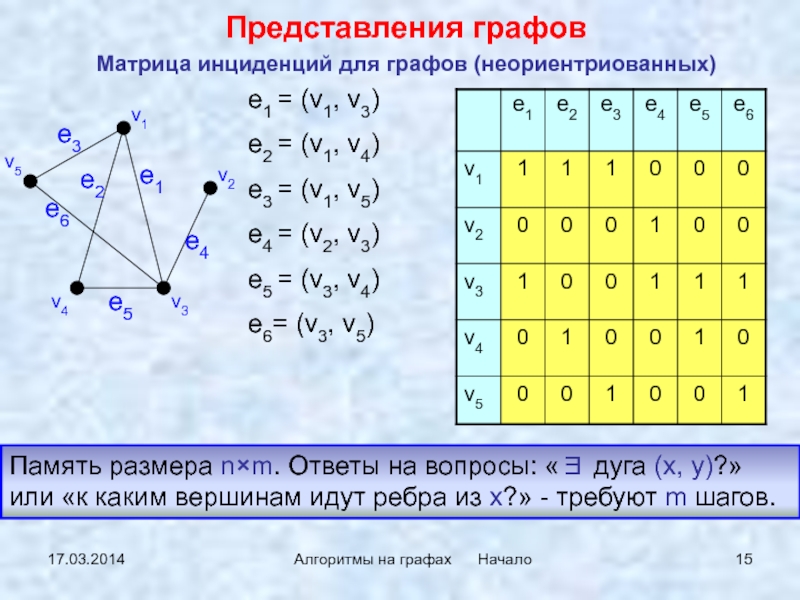
Матрица инциденций для графов (неориентриованных)
Представления
графов
e1 = (v1, v3)
e2 = (v1, v4)
e3 = (v1, v5)
e4
= (v2, v3)e5 = (v3, v4)
e6= (v3, v5)
Память размера n×m. Ответы на вопросы: «∃ дуга (x, y)?» или «к каким вершинам идут ребра из x?» - требуют m шагов.
e1
e2
e3
e4
e5
e6
Слайд 1617.03.2014
Алгоритмы на графах Начало
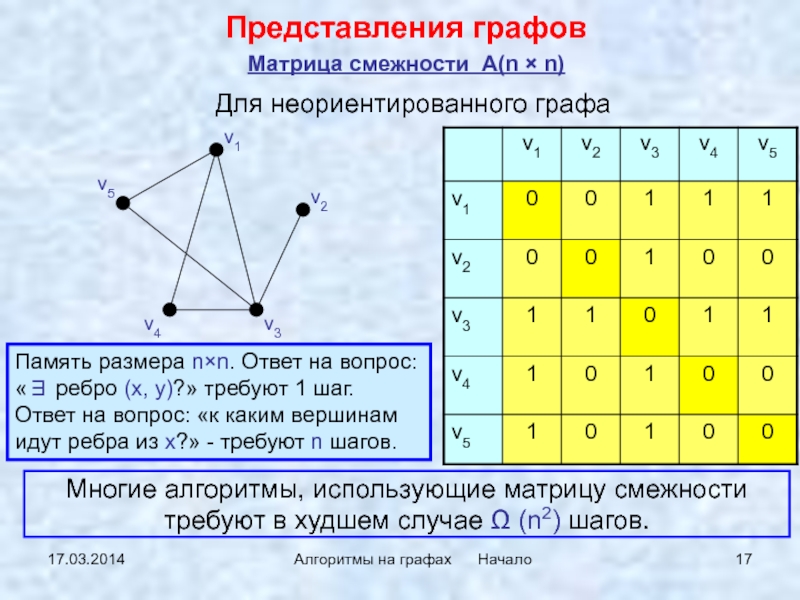
A[u, v] = 1, если
u − v или u → v, иначе A[u, v]
= 0.Для неориентированного графа
матрица смежности симметрична.
Матрица смежности A(n × n)
Представления графов
Слайд 1717.03.2014
Алгоритмы на графах Начало
Для неориентированного графа
Представления графов
Матрица смежности
A(n × n)
Память размера n×n. Ответ на вопрос: «∃ ребро
(x, y)?» требуют 1 шаг.Ответ на вопрос: «к каким вершинам идут ребра из x?» - требуют n шагов.
Многие алгоритмы, использующие матрицу смежности требуют в худшем случае Ω (n2) шагов.
Слайд 1817.03.2014
Алгоритмы на графах Начало
Списки смежности
Adj[1..n] – массив списков
(adjacent – смежный, соседний)
Adj[v] – список вершин, смежных с v.
1
2
3
4
5
6
7
8
9
Adj[1]:
2, 4, 5Adj[2]: 1, 3, 5
Adj[3]: 2, 5, 6
Adj[4]: 1, 7
Adj[5]: 1, 2, 3, 9, 8, 7
Adj[6]: 3, 9
Adj[7]: 4, 5, 8
Adj[8]: 7, 5, 9
Adj[9]: 5, 6, 8
Пример графа (n = 9; m = 14)
Пояснить круговые стрелки!
Слайд 1917.03.2014
Алгоритмы на графах Начало
Списки смежности
Реализация упорядоченного графа
Adj[1..n] –
массив списков (adjacent – смежный, соседний)
Adj[v] – список вершин, смежных
с v.for ∀u∈ Adj[v] do S(u) ≡
begin p := Adj[v].head;
while p ≠ nil do
begin
u := p^.vert;
S(u);
p := p^.next
end
end
Память – (n + 2m)
Представления графов
Слайд 2017.03.2014
Алгоритмы на графах Начало
Списки смежности
for ∀u∈ Adj [v]
do S(u) ≡
begin L := Adj [v].head; {L: L1_List **}
GoBOL(L);
{Встать в начало списка}while not EOList(L) do
begin
GetEl(L,u); {получить текущий элемент u списка L}
S(u);
GoNext(L) {перейти к следующему элементу списка}
end {while}
end
** - см. Учеб. пособие «Динамические СД», 2004
Представления графов
Слайд 2117.03.2014
Алгоритмы на графах Начало
Задание:
Написать код преобразования одного
представления графа (орграфа) в другое.
Виды представления:
матрица инциденций;
матрица смежности;
списки
смежности.Представления графов
Слайд 2517.03.2014
Алгоритмы на графах Начало
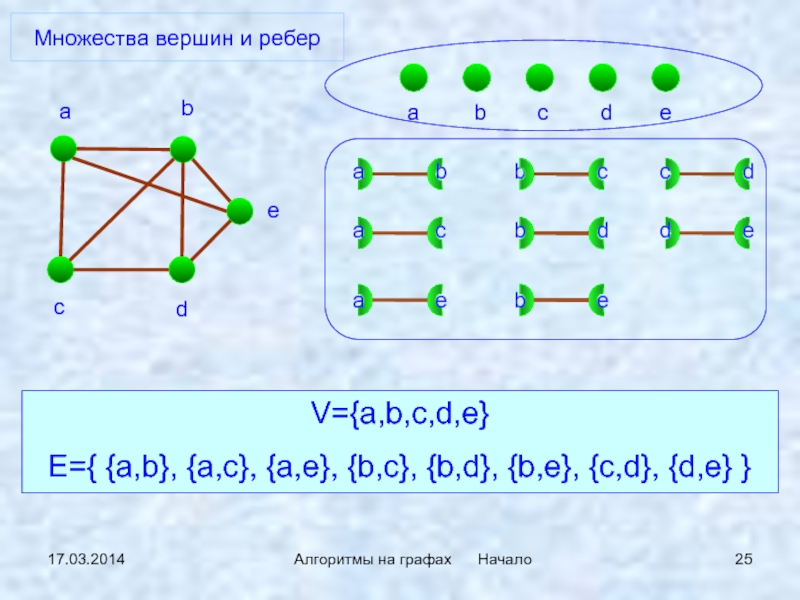
Множества вершин и ребер
V={a,b,c,d,e}
E={ {a,b},
{a,c}, {a,e}, {b,c}, {b,d}, {b,e}, {c,d}, {d,e} }
b
a
a
a
c
d
e
b
c
e
b
b
c
d
e
d
Слайд 2617.03.2014
Алгоритмы на графах Начало
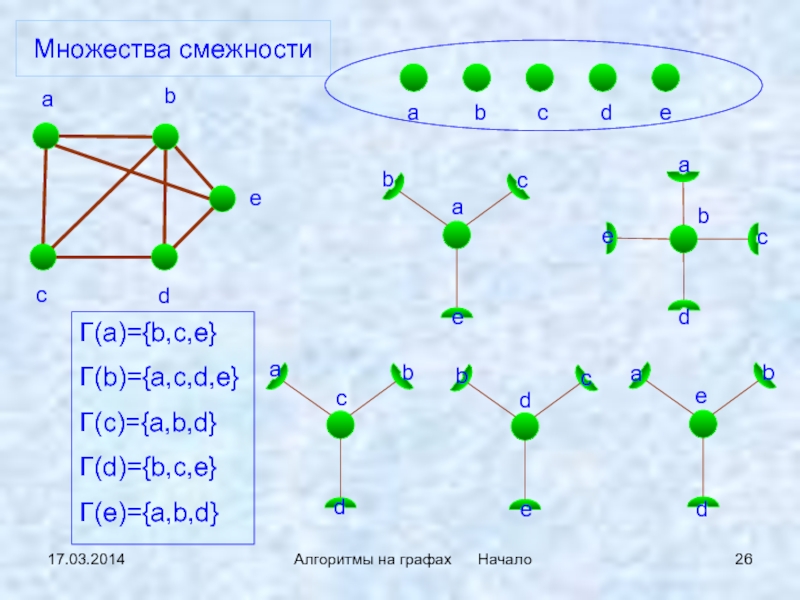
Множества смежности
Γ(a)={b,c,e}
Γ(b)={a,c,d,e}
Γ(c)={a,b,d}
Γ(d)={b,c,e}
Γ(e)={a,b,d}
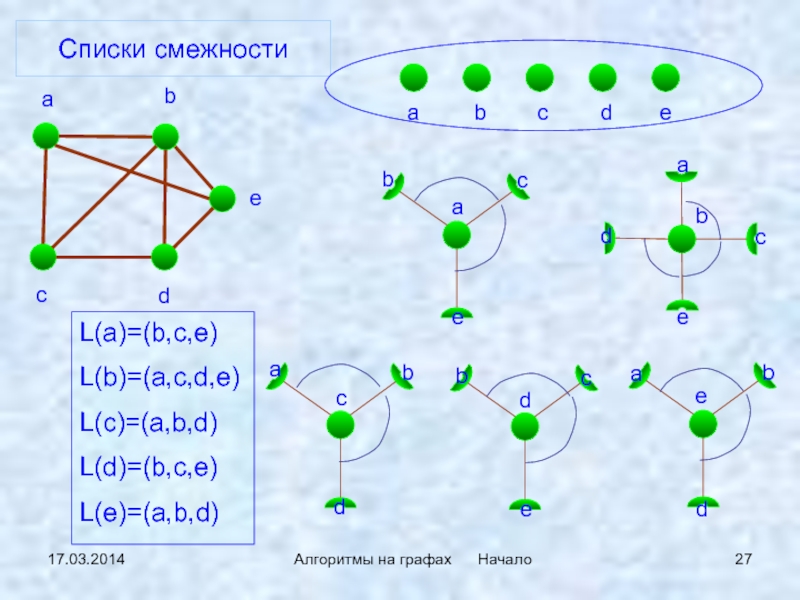
Слайд 2717.03.2014
Алгоритмы на графах Начало
Списки смежности
L(a)=(b,c,e)
L(b)=(a,c,d,e)
L(c)=(a,b,d)
L(d)=(b,c,e)
L(e)=(a,b,d)
Слайд 2917.03.2014
Алгоритмы на графах Начало
Дерево – связный граф, не
содержащий циклов.
Граф связный, если каждая пара различных вершин графа связана
маршрутом.Для связного графа G = (V, E) остовным деревом
(остовом, каркасом, скелетом)
является дерево T = (V, F), где F⊆ E.
В графе много остовов. Например, в полном графе число остовов nn-2.
3. Минимальное остовное дерево
…
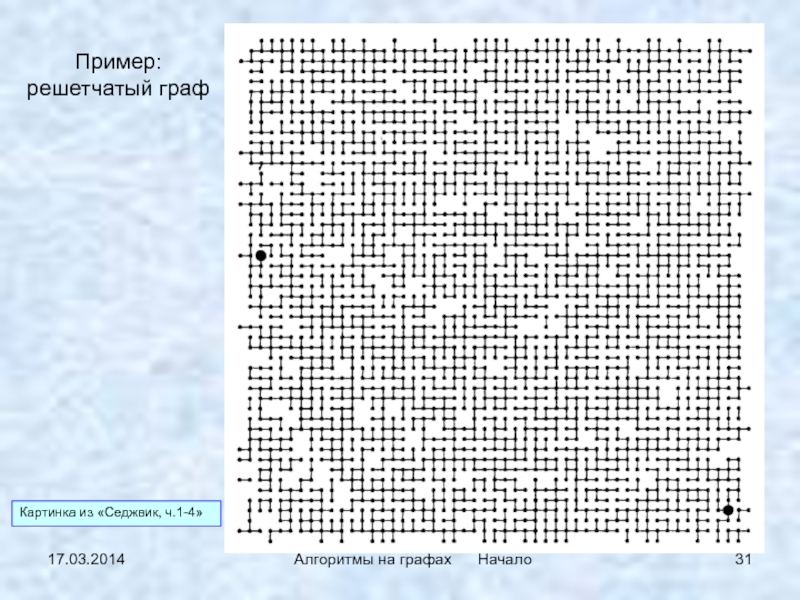
Слайд 3017.03.2014
Алгоритмы на графах Начало
Остовные деревья (леса)
Пример. Задача «связности»
(Седжвик).
Задан граф.
Пусть номера вершин графа есть 1, 2, 3, …,
n Дана пара {i,j}.
Требуется определить, связаны ли вершины i и j путем в графе.
В зависимости от требуемой формы ответа существуют разные виды этой задачи:
Ответ - да/нет
Указать путь из i в j
Найти все пути из i в j
Найти кратчайший путь
Слайд 3217.03.2014
Алгоритмы на графах Начало
Рассмотрим простой вариант задачи связности
Предъявляется
последовательность ребер графа:
i1 – j1, i2 – j2, i3 –
j3,…, im – jmЕсли для очередного ребра i – j оказывается, что в графе нет пути из i в j,
то ребро добавляется в результат.
Если же уже есть путь из i в j,
то ребро игнорируется.
Ясно, что так будет сформировано множество ребер остовного дерева графа (или остовного леса).
Слайд 3317.03.2014
Алгоритмы на графах Начало
Пример графа
(n = 9; m
= 14)
Adj[1]: 2, 4, 5
Adj[2]: 1, 3, 5
Adj[3]: 2, 5,
6Adj[4]: 1, 7
Adj[5]: 1, 2, 3, 9, 8, 7
Adj[6]: 3, 9
Adj[7]: 4, 5, 8
Adj[8]: 7, 5, 9
Ребра:
{1, 2}
{1, 4}
{1, 5}
{2, 3}
{2, 5}
{3, 5}
{3, 6}
{4, 7}
{5, 7}
{5, 8}
{5, 9}
{6, 9}
{7, 8}
{8, 9}
Adj[9]: 5, 6, 8
Слайд 3417.03.2014
Алгоритмы на графах Начало
Пример
Идея: пусть на некотором шаге
сформирован остовный лес (выделены подмножества вершин – деревья остовного леса
– W1, W2, …, WL).Тогда при добавлении ребра:
либо ребро соединяет вершины одного дерева (тогда образуется цикл) и такое ребро отбрасываем,
либо ребро соединяет вершины разных деревьев Ws и Wt и тогда следует объединить Ws и Wt в одно множество.
Слайд 3517.03.2014
Алгоритмы на графах Начало
Алгоритм
for (i = 1; i
while (cin >> p>> q)
{
Найти такие i и j , что p∈Wi и q∈Wj ;
if (i == j) ничего
else {
cout << p <<‘ ‘<< q<< endl;
Объединить Wi и Wj
}
}
Операции НАЙТИ (Wi такое, что p∈Wi) и ОБЪЕДИНИТЬ (Wi и Wj )
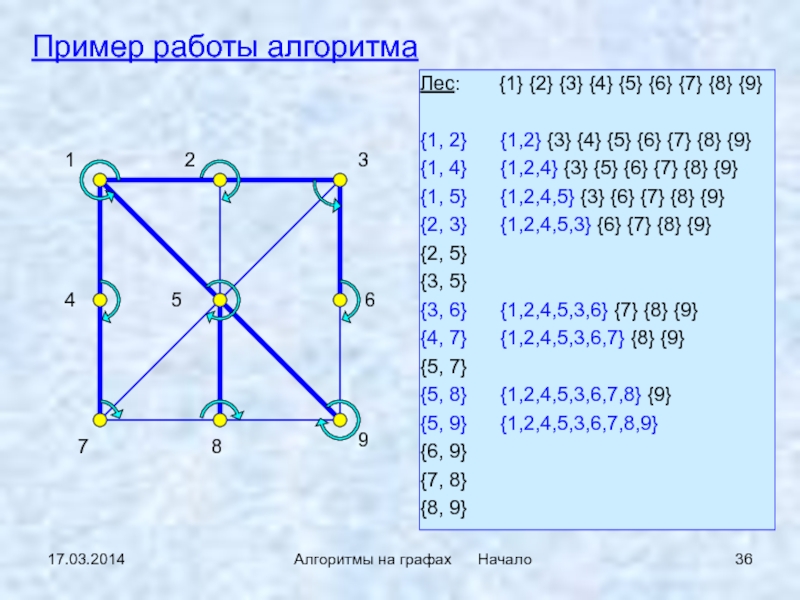
Слайд 3617.03.2014
Алгоритмы на графах Начало
Пример работы алгоритма
Лес:
{1} {2} {3} {4} {5} {6} {7} {8}
{9}{1, 2} {1,2} {3} {4} {5} {6} {7} {8} {9}
{1, 4} {1,2,4} {3} {5} {6} {7} {8} {9}
{1, 5} {1,2,4,5} {3} {6} {7} {8} {9}
{2, 3} {1,2,4,5,3} {6} {7} {8} {9}
{2, 5}
{3, 5}
{3, 6} {1,2,4,5,3,6} {7} {8} {9}
{4, 7} {1,2,4,5,3,6,7} {8} {9}
{5, 7}
{5, 8} {1,2,4,5,3,6,7,8} {9}
{5, 9} {1,2,4,5,3,6,7,8,9}
{6, 9}
{7, 8}
{8, 9}
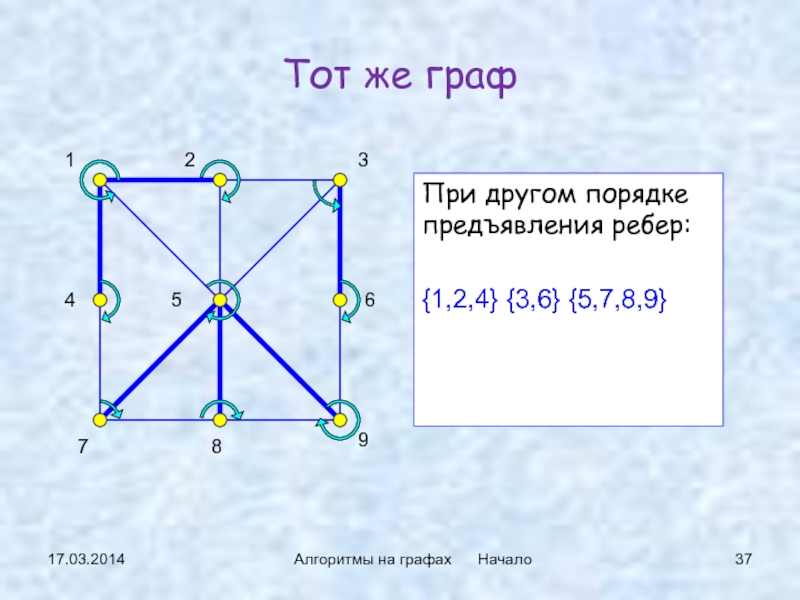
Слайд 3717.03.2014
Алгоритмы на графах Начало
Тот же граф
При другом порядке
предъявления ребер:
{1,2,4} {3,6} {5,7,8,9}
Слайд 3817.03.2014
Алгоритмы на графах Начало
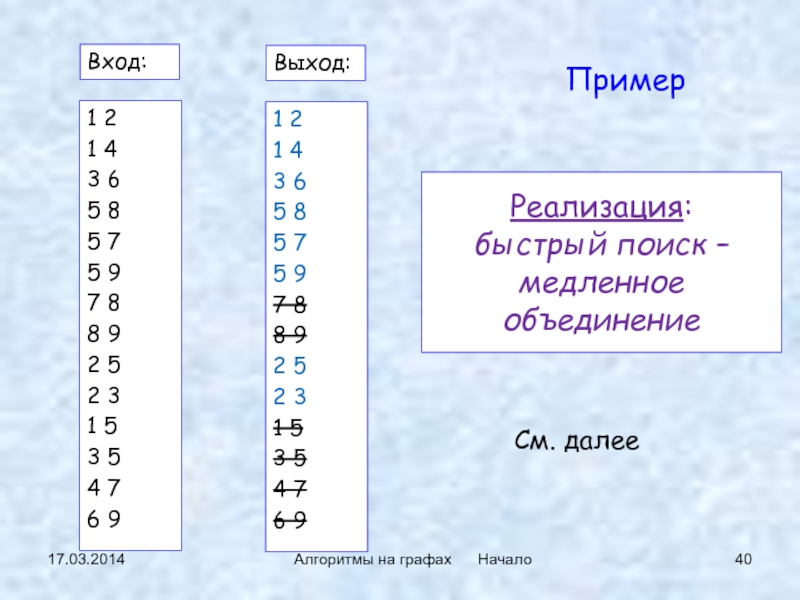
Реализация:
быстрый поиск – медленное
объединение
for (i = 1; i
= i; // w[i] – метка дереваwhile (cin >> p>> q)
{
i = w[p]; j = w[q];
if (i != j)
{ cout << p <<‘ ‘<< q<< endl;
w[p] = j;
for (k = 1; k <= n; k++)
if (w[k] == i) w[k] = j;
}
}
Слайд 39int i, j, k, p, q, w[N];
for (i
= 0; i < N; i++) w[i] = i; //
w[i] – метка дереваwhile (fin >> p >> q){
i = w[p]; j = w[q];
if (i == j) continue;
for (k = 0; k < N; k++)
if (w[k] == i) w[k] = j;
cout << "+ребро: " << p << " " << q << endl;
}
17.03.2014
Алгоритмы на графах Начало
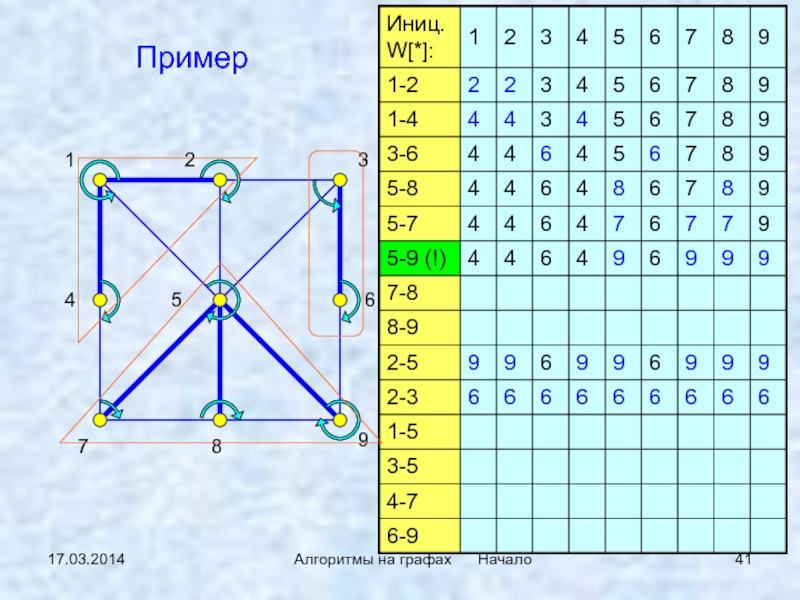
Реализация:
быстрый поиск – медленное объединение
Слайд 401 2
1 4
3 6
5 8
5 7
5
9
7 8
8 9
2 5
2 3
1
5 3 5
4 7
6 9
17.03.2014
Алгоритмы на графах Начало
Вход:
1 2
1 4
3 6
5 8
5 7
5 9
7 8
8 9
2 5
2 3
1 5
3 5
4 7
6 9
Выход:
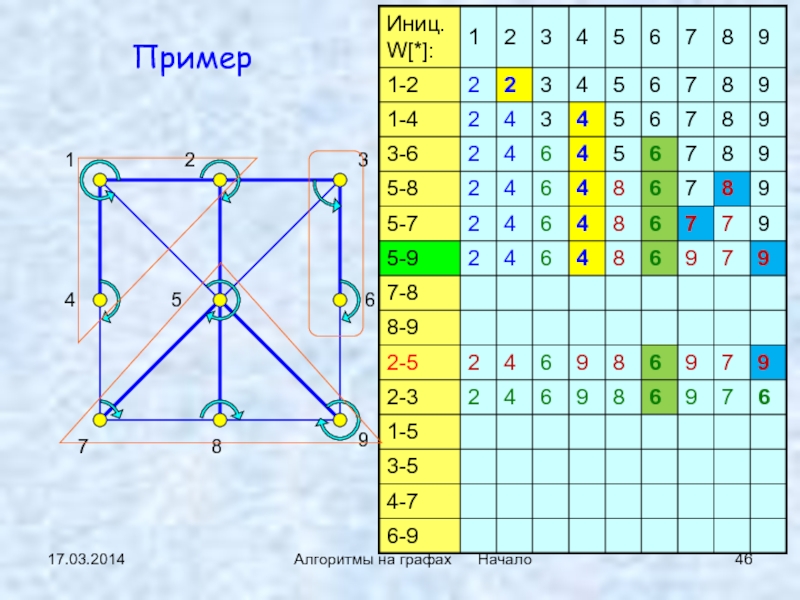
Реализация:
быстрый поиск – медленное объединение
См. далее
Пример
Слайд 431 2
1 4
3 6
5 8
5 7
5
9
7 8
8 9
2 5
2 3
1
5 3 5
4 7
6 9
17.03.2014
Алгоритмы на графах Начало
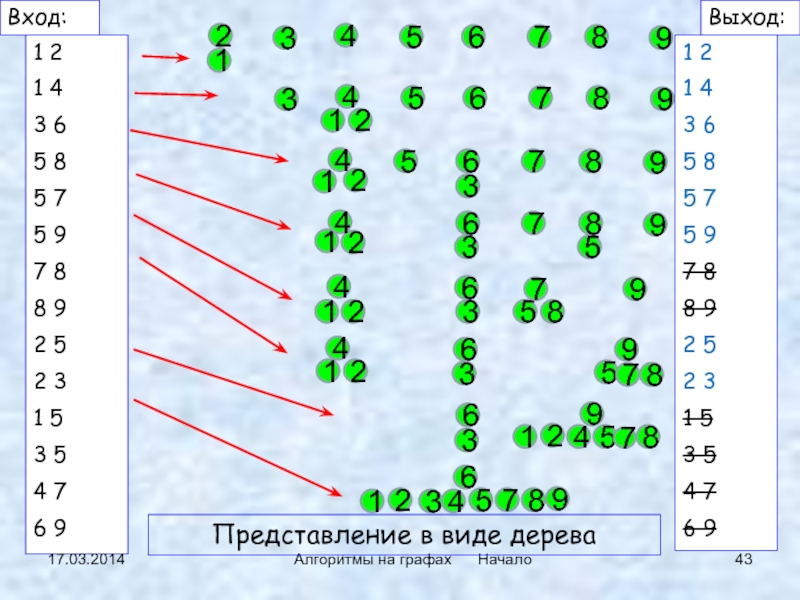
Вход:
1 2
1 4
3 6
5 8
5 7
5 9
7 8
8 9
2 5
2 3
1 5
3 5
4 7
6 9
Выход:
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
Представление в виде дерева
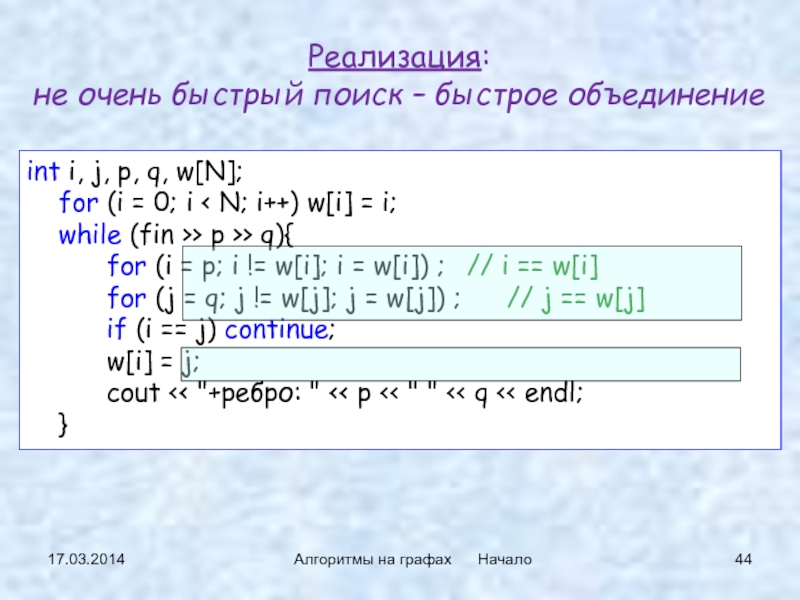
Слайд 44Реализация:
не очень быстрый поиск – быстрое объединение
17.03.2014
Алгоритмы на
графах Начало
int i, j, p, q, w[N];
for (i = 0; i < N; i++) w[i] = i;while (fin >> p >> q){
for (i = p; i != w[i]; i = w[i]) ; // i == w[i]
for (j = q; j != w[j]; j = w[j]) ; // j == w[j]
if (i == j) continue;
w[i] = j;
cout << "+ребро: " << p << " " << q << endl;
}
int i, j, p, q, w[N];
for (i = 0; i < N; i++) w[i] = i;
while (fin >> p >> q){
for (i = p; i != w[i]; i = w[i]) ; // i == w[i]
for (j = q; j != w[j]; j = w[j]) ; // j == w[j]
if (i == j) continue;
w[i] = j;
cout << "+ребро: " << p << " " << q << endl;
}
Слайд 4517.03.2014
Алгоритмы на графах Начало
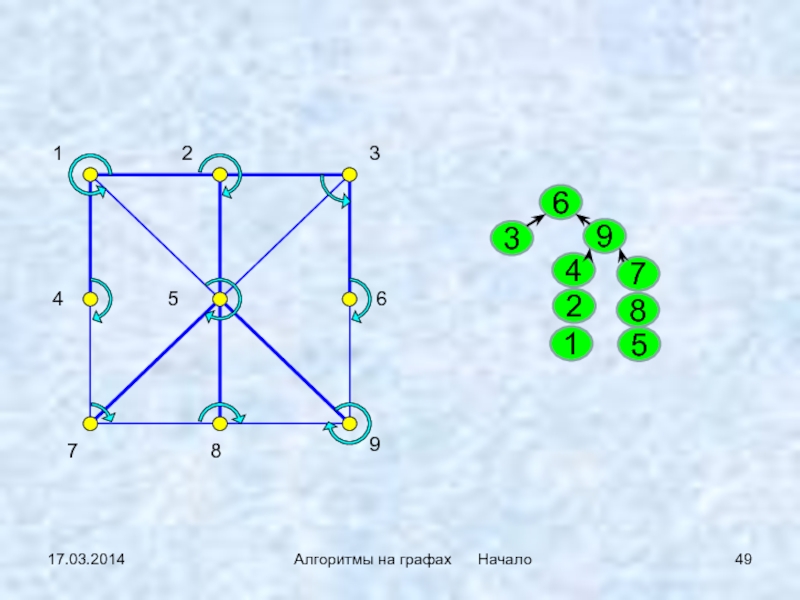
{1,2,4} {3,6} {5,7,8,9}
Реализация:
не очень
быстрый поиск – быстрое объединение
1
2
4
3
6
8
9
7
5
8
9
7
5
6
3
(3,8)
Слайд 471 2
1 4
3 6
5 8
5 7
5
9
7 8
8 9
2 5
2 3
1
5 3 5
4 7
6 9
17.03.2014
Алгоритмы на графах Начало
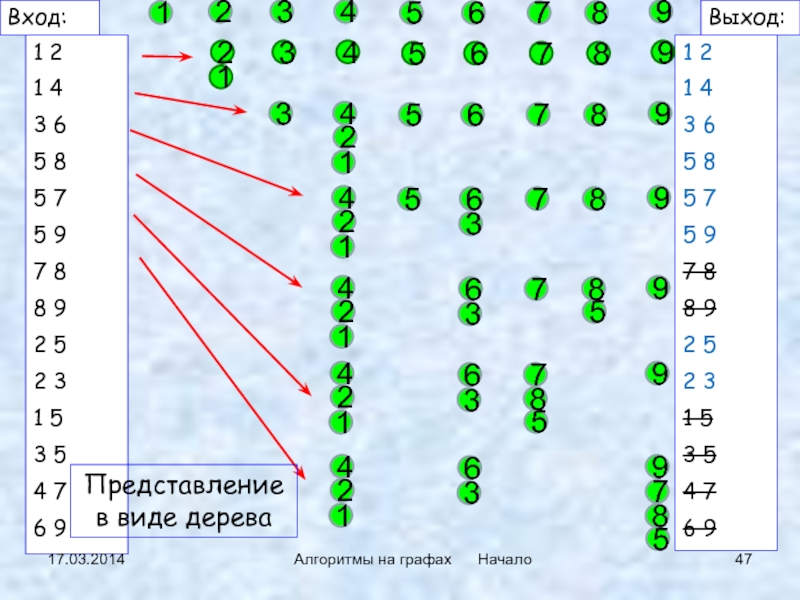
Вход:
1 2
1 4
3 6
5 8
5 7
5 9
7 8
8 9
2 5
2 3
1 5
3 5
4 7
6 9
Выход:
Представление в виде дерева
Слайд 481 2
1 4
3 6
5 8
5 7
5
9
7 8
8 9
2 5
2 3
1
5 3 5
4 7
6 9
17.03.2014
Алгоритмы на графах Начало
Вход:
1 2
1 4
3 6
5 8
5 7
5 9
7 8
8 9
2 5
2 3
1 5
3 5
4 7
6 9
Выход:
Представление в виде дерева
Слайд 5017.03.2014
Алгоритмы на графах Начало
Граф G = (V, E).
Матрица весов W[v, u].
Пусть T = (V, F) –
остов графа. Вес остова определяется как
Минимальное остовное дерево
МОД : TM = Arg min ( W(T) )






![Алгоритмы на графах Графы. Основные определения 17.03.2014Алгоритмы на графах НачалоA[u, v] = 1, если u − 17.03.2014Алгоритмы на графах НачалоA[u, v] = 1, если u − v или u → v,](/img/thumbs/4b0a4172d9f8efd61a45a0f56258a117-800x.jpg)
![Алгоритмы на графах Графы. Основные определения 17.03.2014Алгоритмы на графах НачалоСписки смежности Adj[1..n] – массив списков (adjacent 17.03.2014Алгоритмы на графах НачалоСписки смежности Adj[1..n] – массив списков (adjacent – смежный, соседний) Adj[v] –](/img/thumbs/c869868133fe53a46244cccc5bd6f29a-800x.jpg)
![Алгоритмы на графах Графы. Основные определения 17.03.2014Алгоритмы на графах НачалоСписки смежностиРеализация упорядоченного графаAdj[1..n] – массив списков 17.03.2014Алгоритмы на графах НачалоСписки смежностиРеализация упорядоченного графаAdj[1..n] – массив списков (adjacent – смежный, соседний)Adj[v] –](/img/thumbs/b1f382c45423f7385a8c93447ca5dcc4-800x.jpg)
![Алгоритмы на графах Графы. Основные определения 17.03.2014Алгоритмы на графах НачалоСписки смежностиfor ∀u∈ Adj [v] do S(u) 17.03.2014Алгоритмы на графах НачалоСписки смежностиfor ∀u∈ Adj [v] do S(u) ≡begin L := Adj [v].head;](/img/thumbs/4c2eeb19e4f51b20f06a20e31ed9e1e3-800x.jpg)





![Алгоритмы на графах Графы. Основные определения 17.03.2014Алгоритмы на графах НачалоПример графа (n = 9; m = 17.03.2014Алгоритмы на графах НачалоПример графа (n = 9; m = 14)Adj[1]: 2, 4, 5Adj[2]: 1,](/img/thumbs/b030e86e60079092dcb2dd9116c68991-800x.jpg)



![Алгоритмы на графах Графы. Основные определения int i, j, k, p, q, w[N]; for (i = 0; int i, j, k, p, q, w[N]; for (i = 0; i < N; i++) w[i]](/img/thumbs/7acd6b82547ebdeb6e05e6ea3b7831e6-800x.jpg)


![Алгоритмы на графах Графы. Основные определения 17.03.2014Алгоритмы на графах НачалоГраф G = (V, E). Матрица весов 17.03.2014Алгоритмы на графах НачалоГраф G = (V, E). Матрица весов W[v, u]. Пусть T =](/img/thumbs/7c5378f75215de12efdcb2fdd11fa96a-800x.jpg)