Слайд 1АТОМ ТОМСОНА
Реальность существования атомов.
Электроны являются одной из составляющих атомов.
Существует большое
число различных атомов.
Количество различных атомов не менее числа элементов.
СОВЕРШЕННО НЕ
ЯСНА ВНУТРЕННЯЯ СТРУКТУРА АТОМА
Видимо, она достаточно сложна.
В неё входят электрически заряженные частицы.
Опыты с катодными, каналовыми, анодными лучами.
Атомы способны поглощать и излучать ЭМВ отдельных, характерных для каждого элемента частот.
ПОЛОЖЕНИЕ ВЕЩЕЙ К КОНЦУ 19 ВЕКА
Слайд 2РЕЗУЛЬТАТЫ ОПТИЧЕСКИХ ЭКСПЕРИМЕНТОВ
Бальмер, Лайман и др. показали, что атомы испускают
линейчатые спектры
Johann Jakob Balmer, 1825-1898
швейцарский математик и физик.
Lyman (ЛАЙМАН Теодор)
1874 -1954,
американский физик
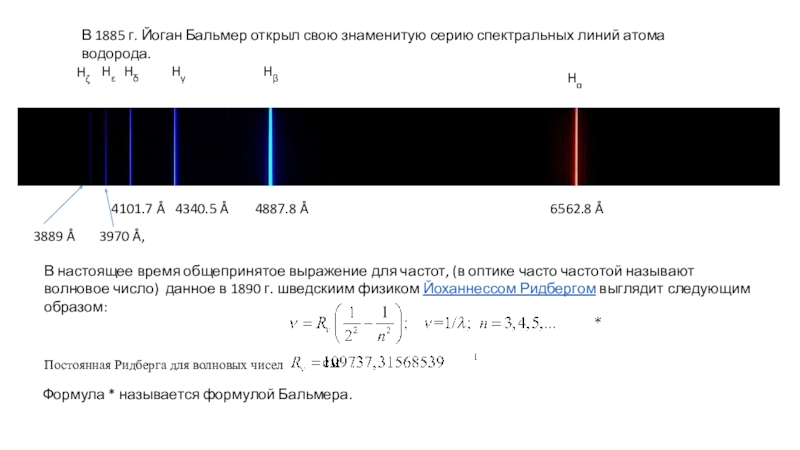
Слайд 3В 1885 г. Йоган Бальмер открыл свою знаменитую серию спектральных
линий атома водорода.
6562.8 Å
3889 Å
3970 Å,
4887.8 Å
4340.5 Å
4101.7 Å
Hα
Hε
Hζ
Hβ
Hγ
Hδ
В настоящее
время общепринятое выражение для частот, (в оптике часто частотой называют волновое число) данное в 1890 г. шведскиим физиком Йоханнессом Ридбергом выглядит следующим образом:
Постоянная Ридберга для волновых чисел
Формула * называется формулой Бальмера.
Слайд 4Своим красным цветом Туманность Ориона обязана нейтральному атомарному водороду, излучающему в
первой линии Бальмера Hα с длиной волны 656,3 нм.
Слайд 5В спектре водорода имеется еще несколько серий. В Ультрафиолетовой области
лежит серия Лаймана:
1906 г.
В инфракрасной области лежат еще несколько серий:
Серия
Пашена
Серия Брэкета
Серия Пфунда
1908 г.
1922 г.
1924 г.
Обобщенная формула Бальмера:
Комбинационный принцип Ритца: «Разность волновых чисел двух спектральных линий одной и той же серии атома даёт волновое число спектральной линии какой-то другой серии того же атома»
Слайд 6МОДЕЛЬ АТОМА ДЖ. ДЖ. ТОМСОНА
Согласно классическим представлениям атом мог бы
испускать монохроматическую ЭМВ, то есть спектральную линию, если электрон в
излучающем атоме совершает гармонические колебания, и, следовательно, удерживается квазиупругой силой вида
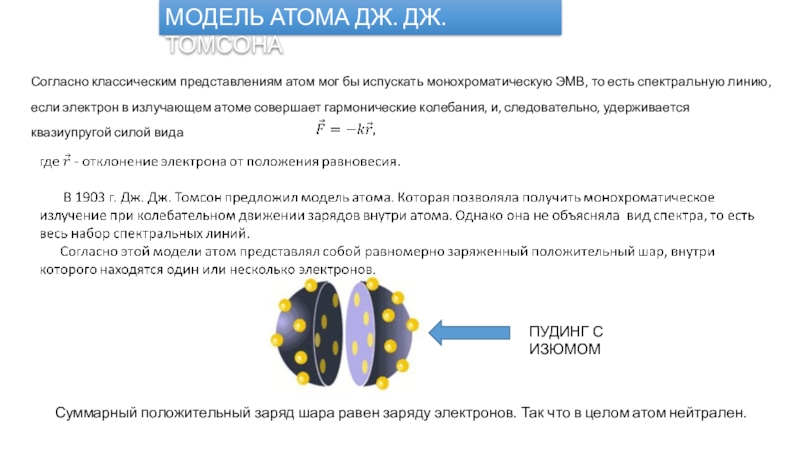
Суммарный положительный заряд шара равен заряду электронов. Так что в целом атом нейтрален.
ПУДИНГ С ИЗЮМОМ
Слайд 7Спектральные линии в томсоновской модели
Пусть положительный заряд e равномерно заполняет
шар радиусом R.
Как было показано в лекции, посвященной электромагнитной массе
электрона, внутри шара напряженность электрического поля зависит от расстояния до центра шара следующим образом:
заряд электрона = -е. Т.е. на электрон действует квазиупругая сила с коэффициентом упругости .
Собственная частота гармонического осциллятора
m – масса электрона.
Слайд 8Модель Томсона позволяет оценить размер атома по наблюдаемым собственным частотам.
Вычислим
частоту, соответствующую головной линии серии Бальмера, λ=656 нм.
Подставляя найденную частоту
и мировые константы, получаем R = 3*10-8 см.
Из эксперимента известно, что спектр излучения реальных атомов хотя и дискретный, как следует из модели Томсона, но зачастую насчитывает сотни, а то и тысячи линий.
Попробуем получить спектральные серии, учтя, что строго гармонические колебания являются математической абстракцией и в природе никогда не осуществляются.
Слайд 9Спектральные серии в томсоновской модели
Рассмотрим спектр строго периодических негармонических колебаний.
Так как у нас колеблется электрон с зарядом «е», то,
как ранее было показано, излучаемая им мощность равна
Введем
Очевидно, что
поэтому можно обозначить
Слайд 11или
Записанный интеграл складывается из суммы интегралов вида
Слайд 12K=-l
Рассмотрим
Следовательно, для
В сумме для остаются
только члены с
K=-l
Слайд 13Сравнивая со средней по времени интенсивностью осциллятора с собственной
частотой
,
Делаем вывод, что средняя мощность излучения
осциллятора, совершающего периодические ангармонические колебания состоит из суммы членов, каждый из которых представляет среднюю мощность осциллятора с частотой, кратной основной гармонике. Таким образом, в этом случае в спектре присутствуют частоты:
Слайд 14Затухание колебаний
До сих пор мы молчаливо предполагали, что энергия осциллятора
остается постоянной. Такое предположение, строго говоря, не отвечает действительности, так
как при колебаниях осциллятора ЭМВ уносит энергию. Ввиду этого запас энергии осциллятора постепенно убывает и колебания затухают.
Найдем закон убывания энергии со временем. Различные экспериментальные данные указывают на то, что затухание излучающих атомов мало. Так, изучение интерференции света при больших разностях хода привело к выводу, что длина ряда волн, испускаемых без затухания соответствует более чем 106 периодов, т.е. для видимого света составляет величину порядка 0.4 ÷ 0.7м. Принимая во внимание это обстоятельство, мы можем сказать, что колебания электрона мало чем отличаются от гармонических. Для последних мы вычислили величину средней энергии уносимой ЭМВ в единицу времени за большой в сравнении с периодом промежуток времени:
Слайд 15Это есть ни что иное как скорость убыли энергии самого
осциллятора.
Полагаем, что излучение начинается в момент времени
.
Полная энергия
гармонического осциллятора, совершающего колебания с амплитудой, равной а:
(127)
(128)
Обозначим
(129)
Слайд 16Тогда (129) перепишется в виде
где
- энергия при
.
Экспоненциальный закон.
γ имеет размерность обратного времени. Соответственно,
обратная величина должна иметь размерность времени:
(132)
Теперь (132) перепишется в виде:
133
Слайд 17- есть промежуток времени, в течение которого энергия убывает в
e раз.
называется временем релаксации.
Определим порядок величины времени релаксации,
на примере голубой линии
водородного спектра, .
Подставляя в (133) это значение круговой частоты, и значения универсальных констант:
найдем
к5л040315
Слайд 18Это показывает, что абсолютная величина времени свечения очень мала. Однако,
отношение времени релаксации к периоду колебаний порядка
То есть электрон должен
совершить 6 миллионов колебаний, прежде чем за счет излучения его энергия уменьшится в е раз.
Непосредственное экспериментальное определение величины времени релаксации было впервые осуществлено при помощи каналовых лучей. Пучок светящихся водородных каналовых лучей через отверстие в катоде выпускался в пространство, где поддерживался столь высокий вакуум, что атомы могли “высвечиваться” практически без соударений. По убыванию интенсивности вдоль светящегося пучка при известной скорости каналовых лучей можно было определить время релаксации. Оказалось, что порядок величины этого времени совпадает с указанным выше для длины волны 500 нм.
Слайд 19Так как мы с большой степенью точности можем положить наши
колебания гармоническими, то их частота остается постоянной, и единственной величиной,
за счет которой может изменяться полная энергия, оказывается амплитуда:
а = а(t). Постольку - поскольку энергия осциллятора – убывающая функция времени, определённая по условиям опыта при , ее максимальное значение достигается при . Амплитуда при будет обозначена как а0.
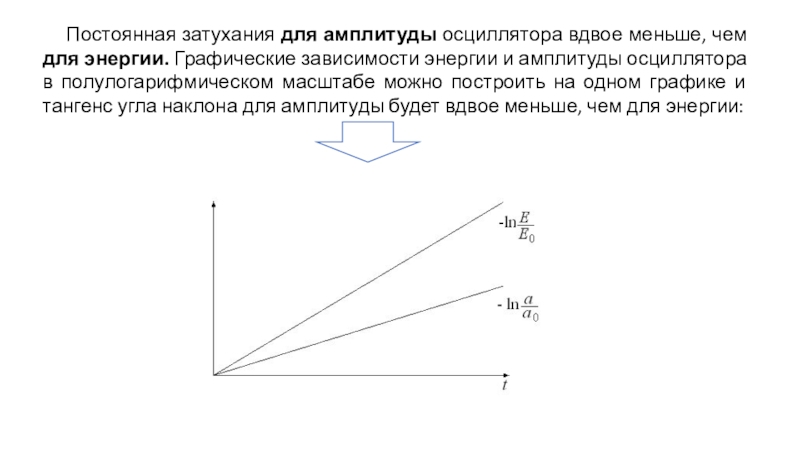
Слайд 20Постоянная затухания для амплитуды осциллятора вдвое меньше, чем для энергии.
Графические зависимости энергии и амплитуды осциллятора в полулогарифмическом масштабе можно
построить на одном графике и тангенс угла наклона для амплитуды будет вдвое меньше, чем для энергии:
Слайд 21ЛУЧИСТОЕ ТРЕНИЕ
Энергия диполя, совершающего колебания слабо затухающие со временем уменьшаются
со временем по экспоненциальному закону. В механике при рассмотрении затухающих
колебаний математического маятника уменьшение энергии маятника может описываться введением эффективной силы трения, которая, как показывает опыт, оказывается пропорциональна первой производной от смещения, то есть скорости.
Аналогичным образом мы попытаемся поступить и в случае затухающих ЭМ колебаний, введя эффективную силу трения. Какова может быть природа этой силы? Так как, естественно, никакого трения в механическом смысле наш осциллятор испытывать не может, то единственной причиной этой эффективной силы трения может быть обратное воздействие ЭМ излучения, возникающего при ускоренном движении заряда на сам, порождающий поле движущийся ускоренно заряд.
Природа «силы лучистого трения» совершенно отлична от природы механической силы трения. у нас нет никаких оснований полагать что эффективная сила трения окажется пропорциональна первой производной от смещения.
Слайд 22ОПРЕДЕЛЕНИЕ ЯВНОГО ВИДА «СИЛЫ ЛУЧИСТОГО ТРЕНИЯ»
Вычислим среднее значение работы силы
лучистого трения за промежуток времени, достаточно большой по сравнению с
периодом колебаний. Обозначим это силу R. Ее работа на участке траектории dx
Среднее значение работы за промежуток времени t
(5.5)
Слайд 23Так как мы работаем только с хорошими функциями, то производные
смещения по времени оказываются функциями ограниченными, поэтому, выбирая интервал времени
по которому производится усреднение достаточно большим, мы можем сделать первое слагаемое в (5.5) сколь угодно малым, в результате останется только второе слагаемое:
В механике силы зависящие от третьей производной смещения по времени неизвестны.
Слайд 24Колебательное движение электрона с учетом затухания
В одномерном случае уравнение движения
электрона с учетом затухания имеет вид
R – сила лучистого трения.
Линейное
дифференциальное уравнение третьего порядка. Будем решать его методом последовательных приближений. В нулевом приближении, учитывая, что радиационное затухание весьма мало, мы пренебрегаем силой лучистого трения и возвращаемся к уравнению осциллятора без учета затухания.
Решение его известно:
- собственная частота незатухающих колебаний.
(5.10)
Слайд 25Выбором начала отсчета нетрудно сделать
, тогда
Третья производная для гармонических колебаний линейно связана
с первой
Такая замена идеологически соответствует наличию эффективной силы трения.
Если мы подставим полученное выражение для производной в (5.10), то:
1. понизим порядок уравнения;
2. получим уравнение с членом пропорциональным первой производной смещения по времени – то есть уравнение аналогичное уравнению механического осциллятора с силой трения;
3. полученное уравнение не будет точно описывать процесс, но есть надежда, что основные черты его будут схвачены.
Слайд 26Решение уравнения движения
Подставим
разделим
на m, перенесем все члены в левую часть,
и введем, как и ранее, обозначение
Слайд 27Так как мы рассматриваем только слабо затухающие колебания, то
и
Два линейно независимых частных решения однородного уравнения второго порядка, поэтому, согласно теории дифференциальных уравнений, общее решение уравнения есть их линейная комбинация
x – вещественная величина (x* = x), а в выражении справа – комплексная, поэтому А и В должны быть комплексными и для них должно выполняться равенство
тогда если
Колебательное движение, при котором амплитуда
убывает со временем по экспоненциальному закону.
Слайд 29ИНТЕГРАЛ ФУРЬЕ И СПЛОШНОЙ СПЕКТР
1. Затухающие колебания осциллятора не удовлетворяет
определению периодичности – неограниченному повторению отклонений через одинаковые промежутки времени.
2. Весь процесс начинается в определенный момент и следовательно простирается не на всю временную шкалу.
3. Разложение в ряд Фурье периодического процесса происходит по частотам ограниченным снизу некоторой минимальной частотой и весь спектр оказывается дискретным разложением по частотам кратным минимальной.
4. Если ограничиться более высокой частотой чем минимальная, то не воспроизведутся самые крупномасштабные детали разлагаемой в спектр периодической кривой.
Рассмотрим вопрос о спектральном разложении непериодических процессов.
Слайд 30Рассмотрим непериодический процесс, описываемый некоторой функцией f(t), которая на интервале
АС изображается кривой АВС, а на границах интервала, т.е. в
точках А и С обращается в нуль. Очевидно, эта функция непериодическая. Однако, мы можем построить на ее основе периодическую функцию, повторим зависимость f(t) с периодом .
Теперь минимальной частотой нашего разложения в ряд Фурье будет частота
и в разложении будут присутствовать частоты кратные минимальной.
Мы можем увеличить эту частоту, доопределив нашу функцию f(t), в более широком интервале, например ЕД, положив f(t) на отрезках ЕА и С D равной нулю. В результате мы получим уже другое разложение, с меньшей минимальной частотой ω2 < ω1 и, соответственно, более густо расположенными спектральными линиями. Очевидно, что период разложения ED можно расширять бесконечно, соответственно, будет бесконечно уменьшаться минимальная частота в разложении и в пределе мы получим непериодический процесс, а наше разложение превратится в непрерывное.
Слайд 31ИНТЕГРАЛ ФУРЬЕ
Пусть дана непериодическая функция f(t), заданая на конечном интервале
времени от –T|2 до + T|2. Если повторить её с
периодом Т, то такая уже периодическая функция может быть разложена в ряд Фурье по экспонентам мнимого аргумента с комплексными амплитудами, причем минимальной частотой в разложении будет
Коэффициенты разложения
Перепишем это выражение, заменив t на ξ
Слайд 32Подставим последнее выражение в ряд Фурье
- есть минимальная частота в
разложении и шаг по частоте с которым происходит суммирование в
разложении, поэтому можно переписать в виде
Переходя в последней сумме к пределу, если он существует , при ,
(соответственно переходя от периодической функции к её непериодическому
пределу f(t), получим так называемый интеграл Фурье :
Слайд 33или
где
возвращаясь к прежним обозначениям
Зависимость коэффициентов разложения непериодической функции от частоты,
то есть спектр непериодического сигнала.
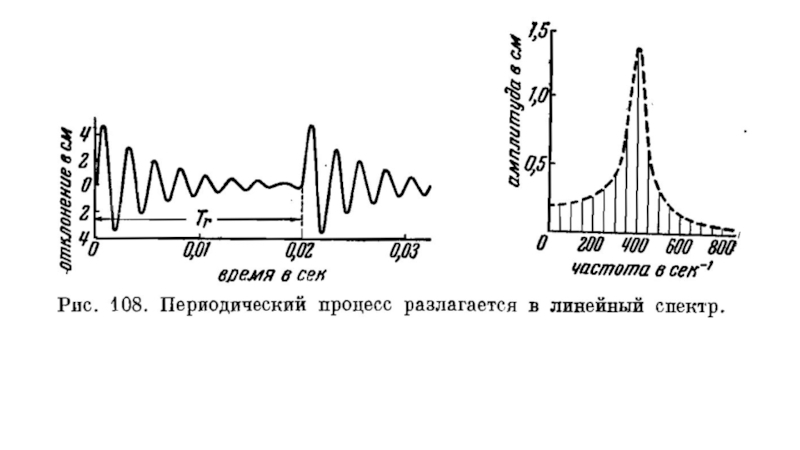
Спектр периодического процесса представляется дискретным набором
амплитуд на частотах кратных минимальной, характерной для данного процесса.
Спектр соответствующего непериодического процесса представляется уже непрерывной спектральной кривой, полностью заполняющей пустые промежутки в спектре предыдущего процесса.
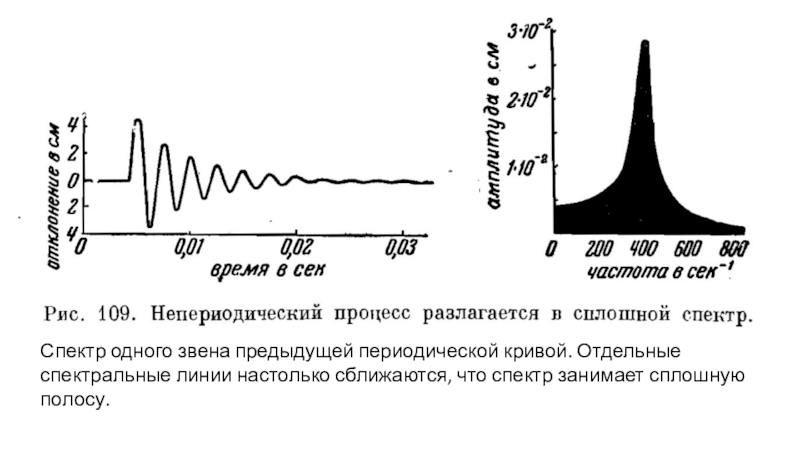
Слайд 35Спектр одного звена предыдущей периодической кривой. Отдельные спектральные линии настолько
сближаются, что спектр занимает сплошную полосу.
Слайд 36ЕСТЕСТВЕННАЯ ШИРИНА СПЕКТРАЛЬНЫХ ЛИНИЙ
но и непериодический процесс, поэтому их спектр
будет представляться не рядом, а интегралом Фурье, то ест спектр
такого процесса будет сплошной. Найдем вид спектра. Будем считать, что функция, спектр которой необходимо определить, задана следующим образом:
Слайд 37Фурье-разложение f(t) имеет вид
Для нашего конкретного случая получаем
Слайд 38Для слабо затухающих колебаний
. Если ограничиться областью частот
вблизи
, то вклад в амплитуду от первого члена будет много меньше,
чем от второго , поэтому
Средняя за период интенсивность излучения
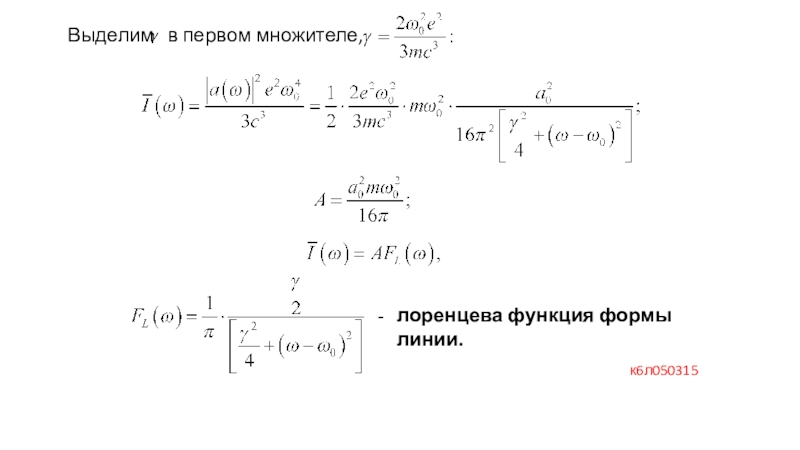
Слайд 39Выделим в первом множителе,
лоренцева функция формы линии.
к6л050315
Слайд 40СВОЙСТВА СПЕКТРА ЗАТУХАЮЩИХ КОЛЕБАНИЙ
1.
2.
имеет максимум
при ;
Ширина линии на половине высоты т.н. «полуширина линии» = :
найдем частоты для которых
Слайд 416. Интегральная интенсивность линии излучения, то есть площадь под кривой
не зависит от коэффициента затухания
в интервале частот от .
Поделим числитель и знаменатель
на
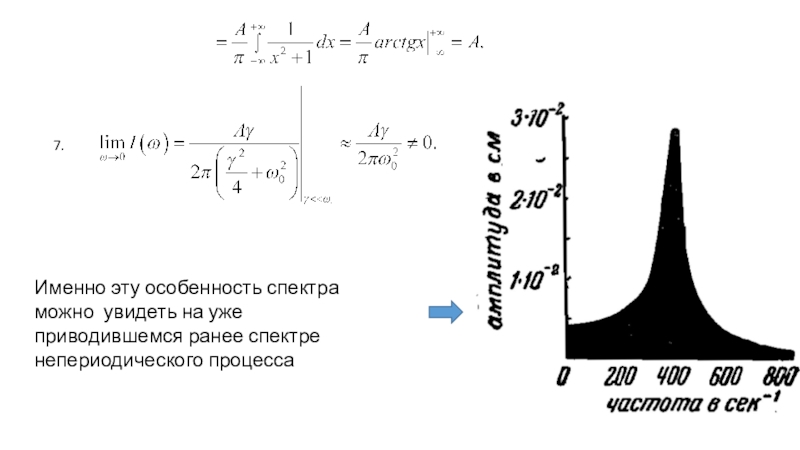
Слайд 427.
Именно эту особенность спектра можно увидеть на уже приводившемся ранее
спектре непериодического процесса
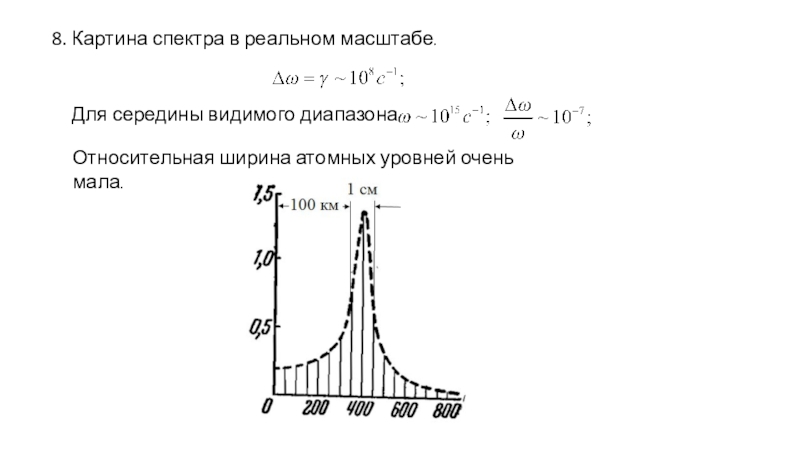
Слайд 438. Картина спектра в реальном масштабе.
Для середины видимого диапазона
Относительная
ширина атомных уровней очень мала.
Слайд 44Сравнение модели атома Томсона с экспериментом
Модель атома, содержащая два вида
электрических зарядов, позволяет в соответствии с экспериментом получить линейчатый спектр.
Спектр
в лучшем случае состоит из эквидистантных по частоте линий. Реальный спектр даже для простейшего водородного атома получить не удалось.
Полуширина линий излучения атомных систем по порядку величины соответствует эксперименту.
Из формулы для собственных частот
следуют разные частоты для атомов различных размеров.
5. Из этой же формулы получается верный порядок размера атомов.