Слайд 1Тема 2. Отношения бинарные и n-арные
Слайд 22.1 Декартово произведение
Декартовым, или прямым произведением
двух множеств А и
В (обозначается А × В) называется множество всех таких упорядоченных пар (a, b),
что a ∈ A и b ∈ В. Пусть, например, А = {a, b, c} и B = {l, m}. Тогда
А × В = {(a, l), (b, l), (c, l), (a, m), (b, m), (c, m)}. Это понятие распространяется на случай с более чем одним сомножителем. Декартово произведение множеств А1, А2, … , Аn (обозначается А1 × А2 × … × Аn) есть множество всех векторов (а1, а2, … , аn)
размерности п, таких, что
a1 ∈ A1, a2 ∈ А2, … , an ∈ Аn.
Слайд 3Декартово произведение n одинаковых сомножителей А × А × … × А обозначается символом Аn и
называется n-й степенью множества А. При этом А1 = А. Примером декартова
произведения является R × R = R2 – множество точек на плоскости. Здесь элементы х ∈ R и у ∈ R служат координатами некоторой точки на плоскости. Другим примером является множество R3 точек в трехмерном евклидовом пространстве. Обобщением этих понятий является n ‑мерное пространство.
Слайд 4 Любое подмножество R ⊆ А1 × А2 × … × Аn декартова произведения п множеств называется
n-арным отношением. При n = 1, 2, 3 имеем унарное, бинарное, тернарное отношения соответственно.
Унарное отношение на множестве А представляет собой подмножество множества А.
Слайд 52.2 Бинарные отношения (соответствия)
Бинарным отношением, или соответствием между элементами
множеств А и В, называется любое подмножество R ⊆ А × В декартова произведения
этих множеств. Тот факт, что некоторые a ∈ A и b ∈ В находятся в отношении R, иногда выражают как a R b. В качестве примера бинарного отношения рассмотрим отношение R между элементами множеств А = {1, 2, 3} и B = {1, 2, 3, 4, 5, 6}, которое можно выразить словами так: элемент х ∈ A есть делитель элемента у ∈ В. Тогда имеем
R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5),
(1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6)}.
Слайд 6 Бинарное отношение удобно представлять в виде двоичной (булевой)
матрицы. При этом элементы множеств А и В должны быть
пронумерованы, и если i-й элемент множества А соответствует j-му элементу множества В, то элемент матрицы, расположенный на пересечении i-й строки и j-го столбца, имеет значение 1, в противном случае он имеет значение 0.
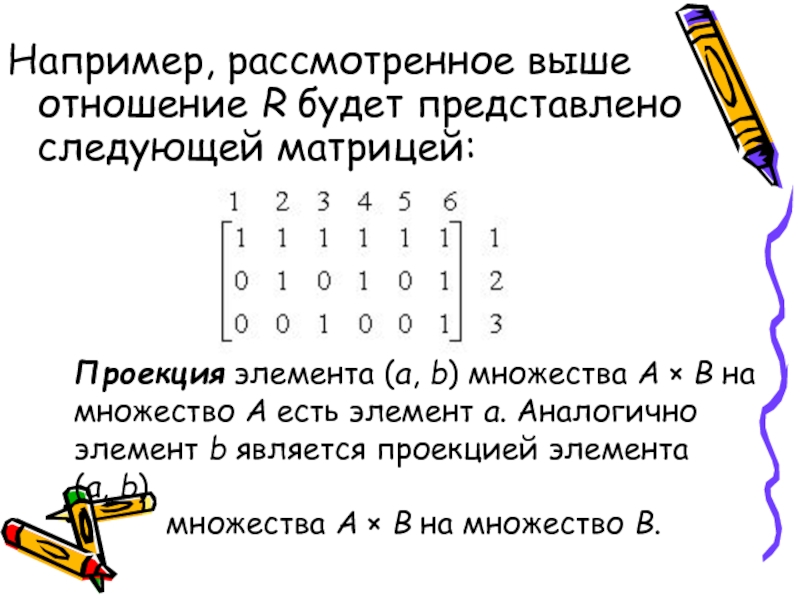
Слайд 7Например, рассмотренное выше отношение R будет представлено следующей матрицей:
Проекция элемента
(a, b) множества А × В на множество А есть элемент а. Аналогично
элемент b является проекцией элемента (a, b)
множества А × В на множество В.
Слайд 8Проекцией множества Е ⊂ А × В на А называется множество всех тех элементов
из А, которые являются проекциями элементов из Е на множество
А. Для множеств А и В, рассмотренных выше, проекцией элемента (2, 4) на множество А является элемент 2, а проекцией множества {(1, 2), (2, 2), (2, 4)} – множество {1, 2}.
Слайд 9Сечением множества R ⊂ А × В по а, обозначаемым R(а), называется множество всех
тех элементов у ∈ В, для которых (a, у)∈ R.
Сечением R(Х) множества R по
Х ⊂ А является объединение сечений для всех элементов из Х.
Пусть R = {(1, 1), (1, 3) (1, 5), (1, 6), (2, 2), (2, 4), (3, 3), (3, 6)}.
Тогда R(2) = {2, 4}, а если Х = {2, 3}, то
R(Х) = {2, 3, 4, 6}.
Слайд 10Бинарное отношение можно задавать с помощью сечений. Например, отношение, представленное
матрицей
можно задать следующим образом:
R(a1) = {b1, b3}, R(a2) = {b1, b3, b4},
R(a3) = {b1, b4}, R(a4) = ∅, R(a5) = {b4}.
Множество сечений для всех a ∈ A
называется фактор-множеством.
Слайд 11Областью определения отношения R ⊆ А × В является проекция множества R на А.
Для рассматриваемого выше отношения такой областью является {а1, а2, а3, а5}. Областью значений
отношения R ⊆ А × В является сечение множества R по А. Областью значений рассматриваемого отношения R является {b1, b3, b4}.
Слайд 12Образом множества Х ⊆ А относительно
R называется множество {b / b ∈ В, х ∈ Х, (х, b) ∈ R}.
Прообразом множества Y ⊆ В относительно R называется множество {a / a ∈ A, y ∈ Y, (a, y) ∈ R}.
В нашем последнем примере образом множества {а1, а3} относительно R является {b1, b3, b4}, а прообразом множества {b3, b4} является {а1, а2, а3, а5}.
Слайд 13 Обратным отношением R – 1
для некоторого отношения R ⊆ А × В является множество,
образованное теми парами (b, а) ∈ В × А, для которых (а, b) ∈ R. Матрица, представляющая отношение
R – 1, получается транспонированием матрицы, представляющей R, т. е. заменой строк столбцами и
наоборот.
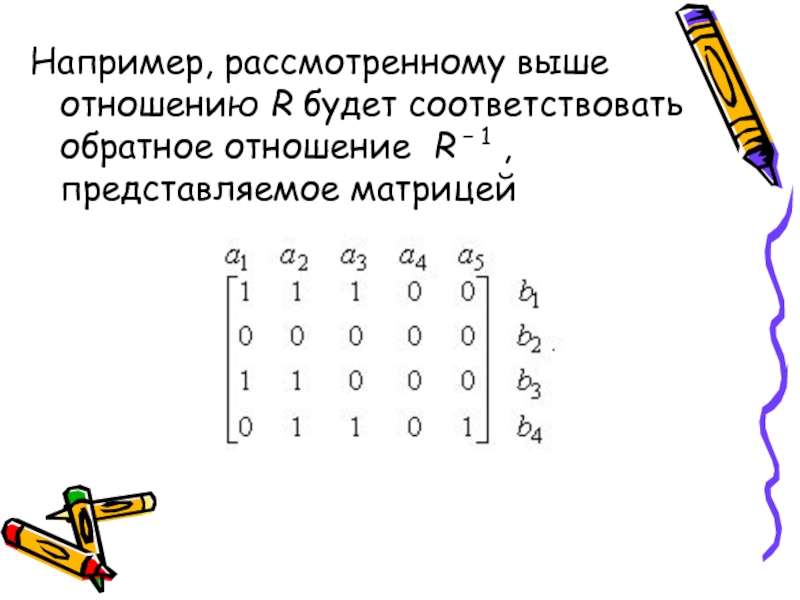
Слайд 14Например, рассмотренному выше отношению R будет соответствовать обратное отношение R − 1
, представляемое матрицей
Слайд 152.3 Операции над бинарными отношениями
Поскольку всякое отношение есть некоторое множество
пар, над отношениями применимы все стандартные операции над множествами, т. е.
объединение, пересечение, дополнение. Универсальным множеством для операции дополнения при этом является А × В.
Слайд 16Рассмотрим операцию композиции отношений. Заданы множества А, В, С и
отношения R ⊆ А × В и S ⊆ В × С. Композиция отношений S и R (обозначается
SR, не путать с пересечением множеств S и R!) – это такое отношение между элементами множеств А и С, что для всех а ∈ А сечение множества SR по а совпадает с сечением множества S по подмножеству R(a) ⊆ B. Это записывается в виде (SR)(a) ⊆ S(R(a)).
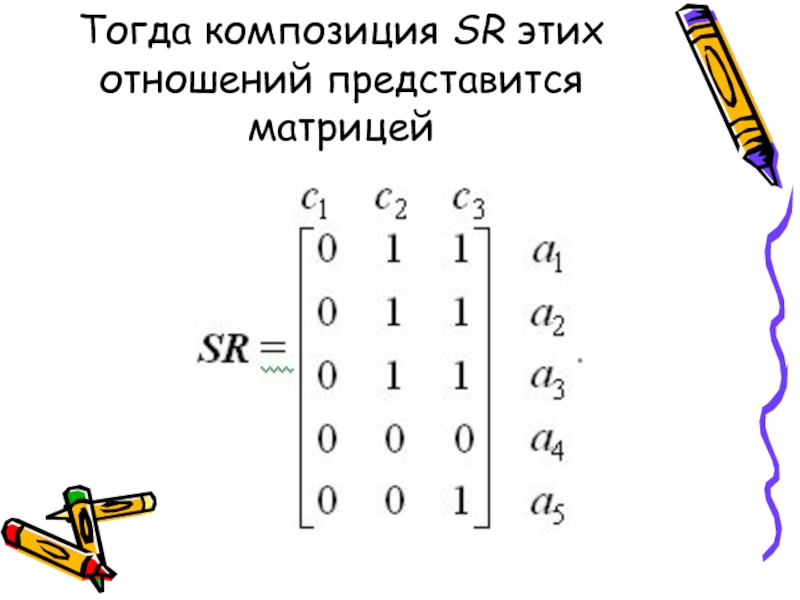
Слайд 17Пример. Пусть отношения R и S заданы соответственно следующими матрицами:
Слайд 18Тогда композиция SR этих отношений представится матрицей
Слайд 192.4 Функциональные отношения
Отношение R ⊆ А × В называется функциональным, если для каждого а ∈ А
сечение множества R по а содержит не более одного элемента,
т.е. для каждого а справедливо |{a / (a, b) ∈ R, b ∈ B}| ≤ 1.
Слайд 20В функциональном отношении не существует пар с одинаковым ле-
вым
элементом и различными правыми элементами, т. е. если (а, b) ∈ R и R
– функциональное отношение, то в R не может быть пары вида (а, с), где b ≠ c. Матрица, представляющая функциональное отношение, в каждой строке имеет не
более одной единицы.
Слайд 21Примером может служить следующая матрица:
Слайд 22Если сечение функционального отношения R по любому элементу а из
множества А содержит один и только один элемент, то отношение
R называется всюду определенным.
Если отношение R –1, обратное для функционального отношения R, также является функциональным, то отношение R называется взаимно однозначным.
Слайд 23Для всякого функционального отношения R ⊆ А × В можно определить функцию, связанную с
этим отношением. Для обозначения функции используется запись f : A → B. Если (х, у) ∈ R,
то это можно выразить как у = f(x), где х является аргументом, а у –
значением функции f.
Слайд 24Множество {x / (x, y) ∈ R} называется областью определения функции f. Если это множество
совпадает с А, то функция f является всюду определенной. Такая
функция называется отображением множества А в В. В противном случае функцию называют частичной.
Слайд 25Множество {у / (x, y) ∈ R} называется областью значений функции f. Если область значений
функции f совпадает с множеством В, то f называют отображением
А на В, сюръективным отображением, или сюръекцией. Обязательным условием существования отображения А на В является |А| ≥ |В|.
Слайд 26Если функциональное отношение R ⊆ А × В, определяющее функцию f, является взаимно однозначным,
то функцию f называют инъективным отображением, или инъекцией. В этом
случае существует функция f – 1, которая является обратной к функции f. При этом если у = f (x), то х = f –1(у), а мощность области определения функции f не должна превышать |В|.
Слайд 27Функция f называется биективным отображением, или биекцией, если она является
как сюръективным, так и инъективным отображением. Такое отображение называется еще
1-1 соответствием.
Если R – взаимно однозначное отношение между элементами одного и того же множества, т. е. R ⊆ А × А = А2, и, кроме того, R и R –1 всюду определены, то отображение, связанное с R, называется
подстановкой.
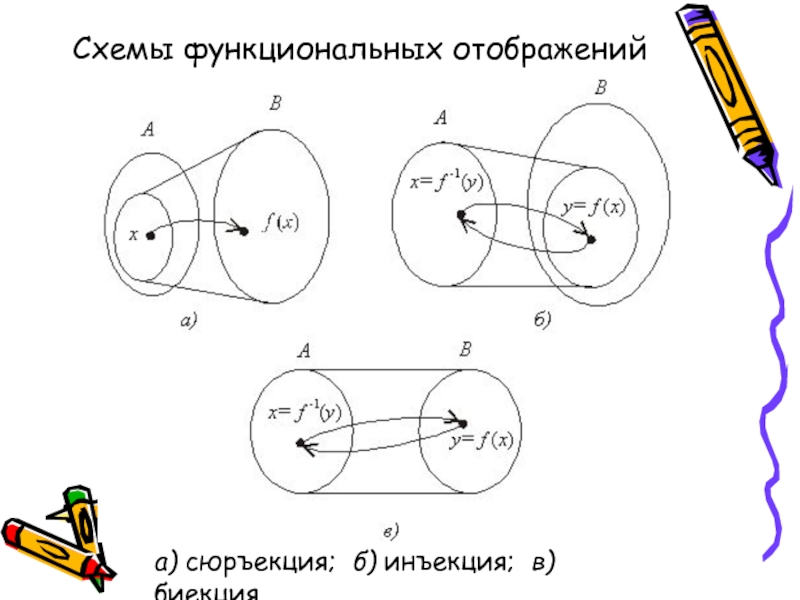
Слайд 28Схемы функциональных отображений
а) сюръекция; б) инъекция; в) биекция
Слайд 29Функция, определенная на множестве натуральных чисел, называется последовательностью, а каждое
ее значение – членом последовательности.
Отображение f произвольного множества в множество
действительных чисел называется функционалом. Примером функционала может служить определенный интеграл.
Слайд 30Отображение f : A → B, где А и В – некоторые множества функций,
называется оператором. Оператор преобразует одну функцию в другую. Примером оператора
является оператор суперпозиции функций, где аргументами некоторых функций служат другие функции.
Слайд 312.5 Бинарные отношения на множестве
Пусть R ⊆ А × А. Определим некоторые свойства, которыми
может обладать или не обладать такое отношение:
рефлексивность: если a = b, то
a R b;
иррефлексивность: если a R b, то a ≠ b;
симметричность: если a R b, то b R a;
антисимметричность: если a R b и b R a, то a = b;
транзитивность: если a R b и b R с, то a R с;
дихотомия: если a ≠ b, то либо a R b, либо b R a.
Слайд 32Типы бинарных отношений, характеризуемые определенным
набором свойств
Отношение эквивалентности рефлексивно,
симметрично и транзитивно. Примерами отношения эквивалентности являются равносильность формул, подобие
геометрических фигур, принадлежность студентов к одной группе, принадлежность населенных пунктов к одному району и т. п.
Слайд 33 Отношение эквивалентности делит множест-во на непересекающиеся подмножества –
классы эквивалентности. С другой стороны, всякое разбиение множества М на
непересекающиеся подмножества задает отношение эквивалентности на множестве М: любые два элемента, принадлежащие одному и тому же классу разбиения, эквивалентны, а элементы, принадлежащие различным классам, не являются эквивалентными. Множество всех классов эквивалентности образует фактор-множество множества М по R (обозначается M / R).
Слайд 34Отношение совместимости рефлексивно и симметрично. Примерами отношения совместимости являются близость
чисел, знакомство людей и т. п.
Отношение нестрогого порядка рефлексивно, антисимметрично и
транзитивно. Отношения ≤ (меньше или равно) и ≥ (больше или равно) для действительных чисел так же, как ⊆ и ⊇ для множеств являются отношениями нестрогого порядка.
Отношение строгого порядка иррефлек-сивно, антисимметрично и транзитивно. Отношениями строгого порядка являются < (меньше) и >
(больше) для действительных
чисел, а также ⊂ и ⊃ для множеств.
Слайд 35Множество М, на котором задано отношение порядка R (строгого или
нестрогого), может быть полностью упорядоченным, если любые два элемента a
и b из М находятся в отношении R, т. е. a R b или b R a. При этом говорят, что a и b сравнимы. Если М содержит хотя бы одну пару элементов с и d, для которых не имеет место ни c R d, ни d R c, то множество М является частично упорядоченным, а указанные элементы с и d несравнимы. Отношение полного порядка обладает свойствами иррефлексивности, антисимметричности и дихотомии. Полный порядок называют еще линейным или
совершенным.
Слайд 36Для множества действительных чисел R отношения ≤ и < являются
отношениями полного порядка. Для семейства подмножеств некоторого множества М отношение
⊆ является отношением частичного порядка. Например, {a1, a3} ⊆ {a1, a2, a3}, а подмножества {a1, a3} и {a1, a2, a4} несравнимы
Слайд 37Порядок букв в алфавите и естественный порядок цифр являются полными
порядками. На основе порядка букв строится лексикографический порядок слов, используемый
в словарях и определяемый следующим образом.
Обозначим это отношение порядка символом . Пусть имеются слова w1 = a11a12 … a1m и w2 = a21a22 … a2n. Тогда w1w2, если и только если либо w1 = paiq, w2 = pajr и аiaj, где p, q и r – некоторые слова, возможно, пустые, а аi и aj – буквы, либо w2 = w1p, где р – непустое
слово.
Слайд 38Например, учебник < ученик и мор < море. В первом
случае р = уче, аi = б, аj = н, q = ник, r = ик, и в алфавите буква
«н» стоит дальше буквы «б». Потому в словаре слово «ученик» следует искать после слова «учебник». Во втором случае w1 = мор и р = е. Согласно лексикографическому порядку слово «море» должно быть помещено в словаре после слова «мор».