БИОМЕХАНИКА

Противоположно пластичности:
Пластичность – способность материала без разрушения получать большие

остаточные деформации.
Текучесть-свойство пластичных металлов и тел при постепенном увеличении давления уступать действию сдвигающих сил и течь подобно вязким жидкостям.
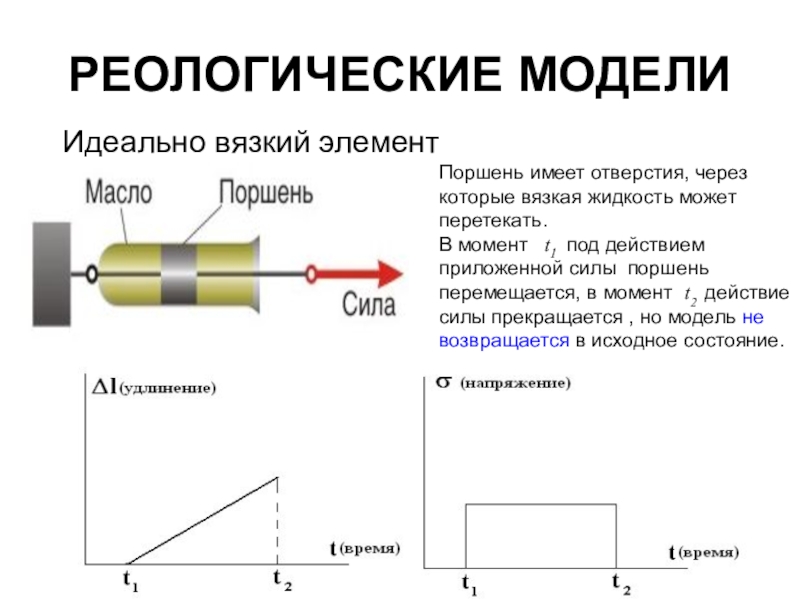
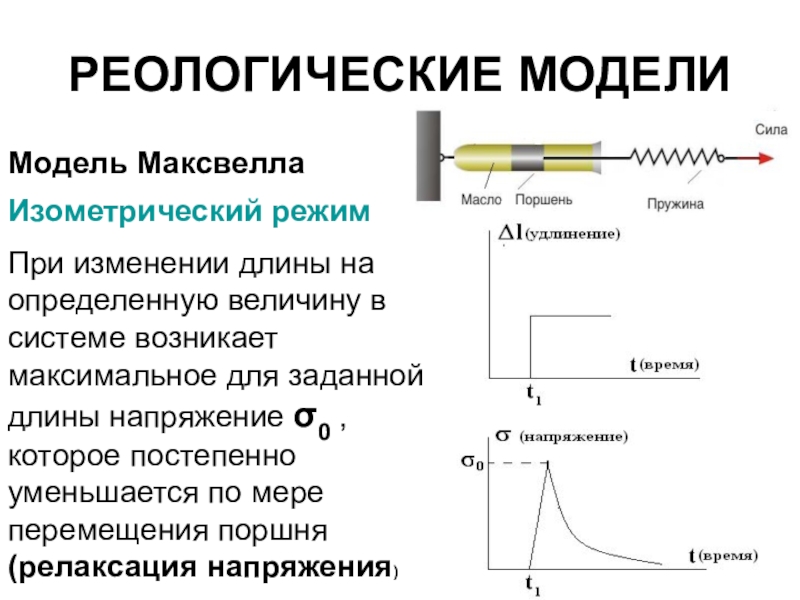
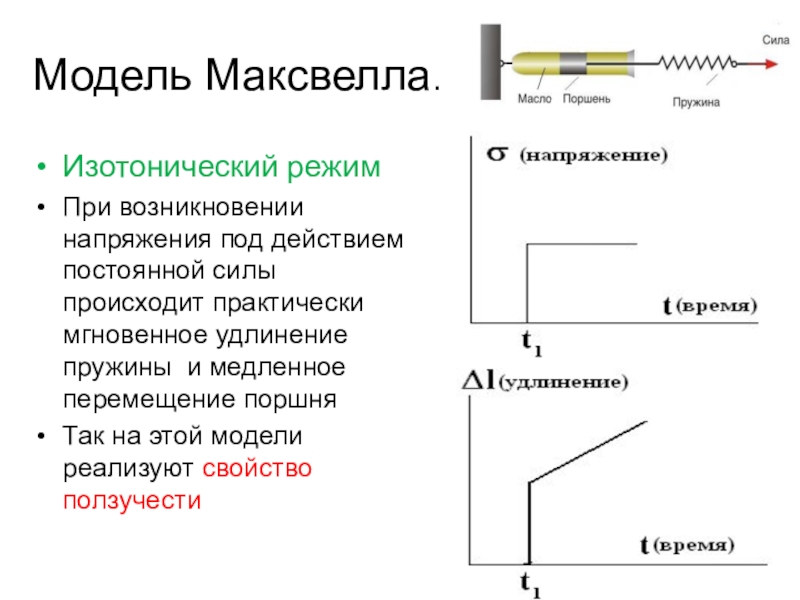
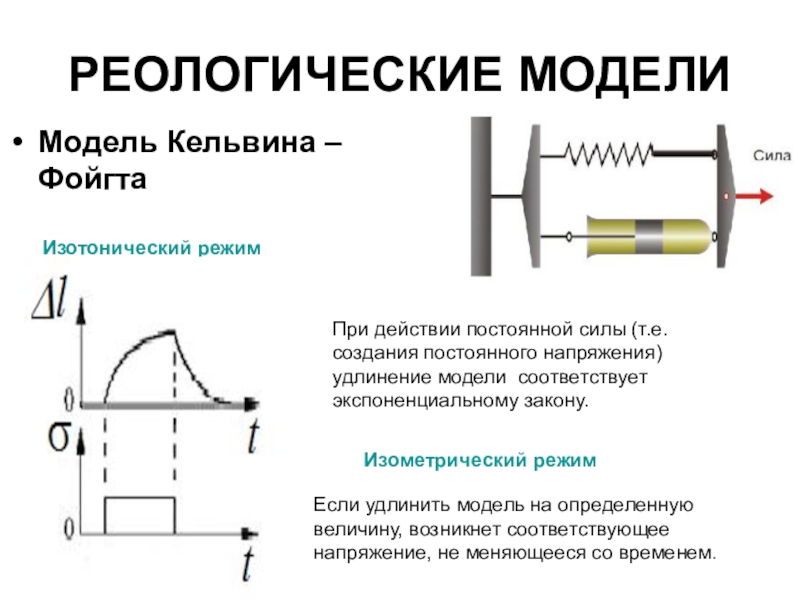
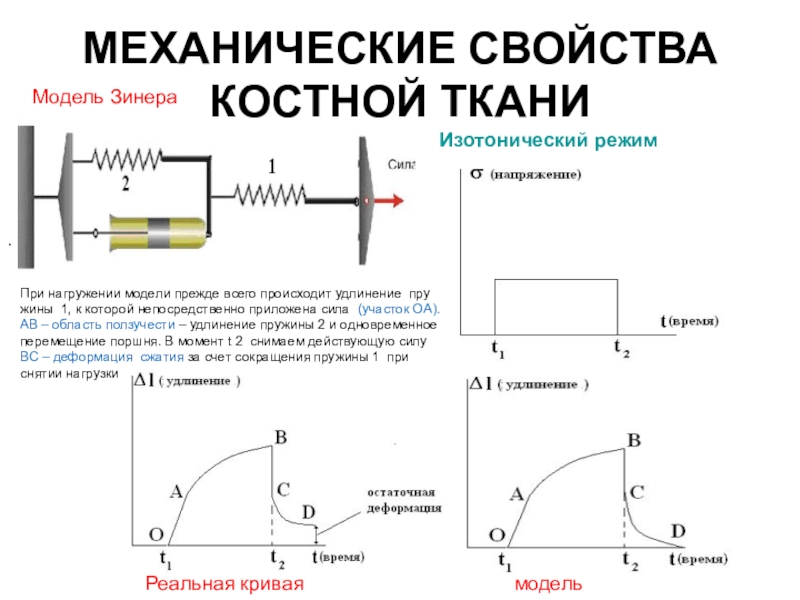
Ползучесть — медленная деформация твёрдого тела под воздействием постоянной нагрузки или механического напряжения.
Вязкость - свойство текучих тел оказывать сопротивление перемещению одной их части относительно другой.
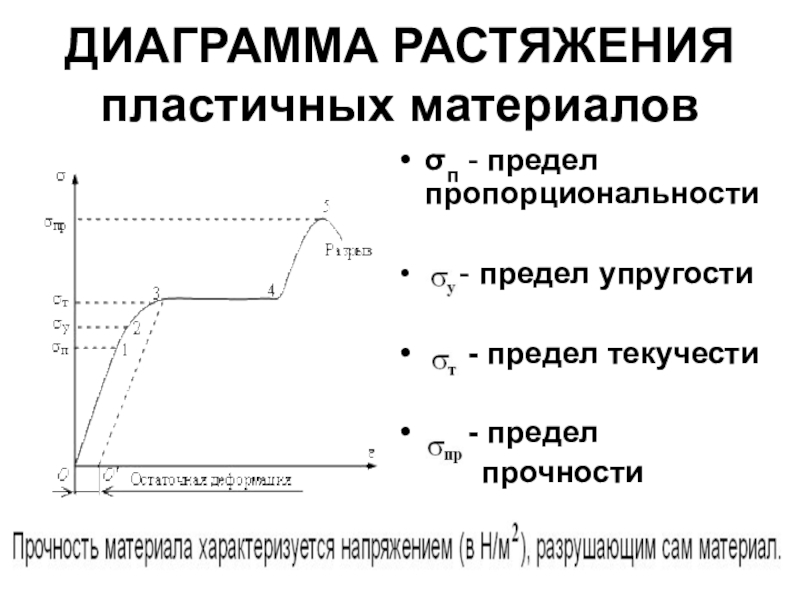
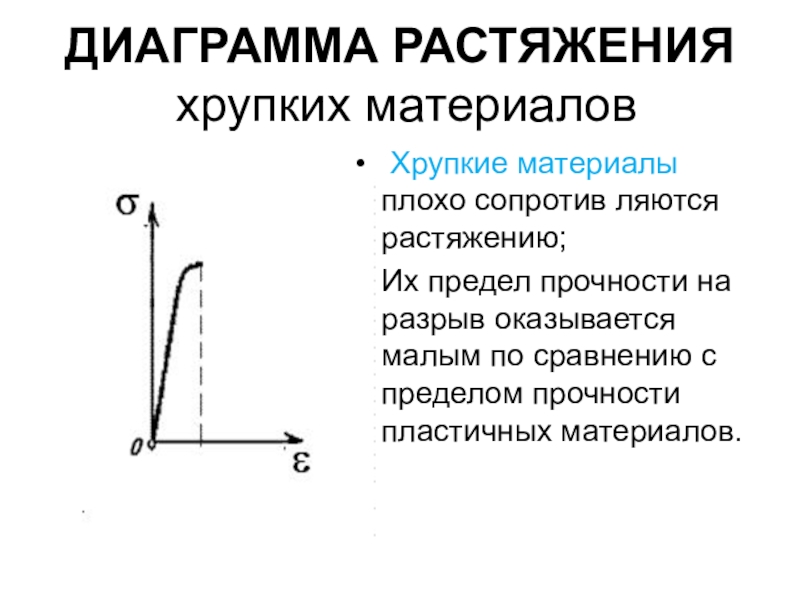
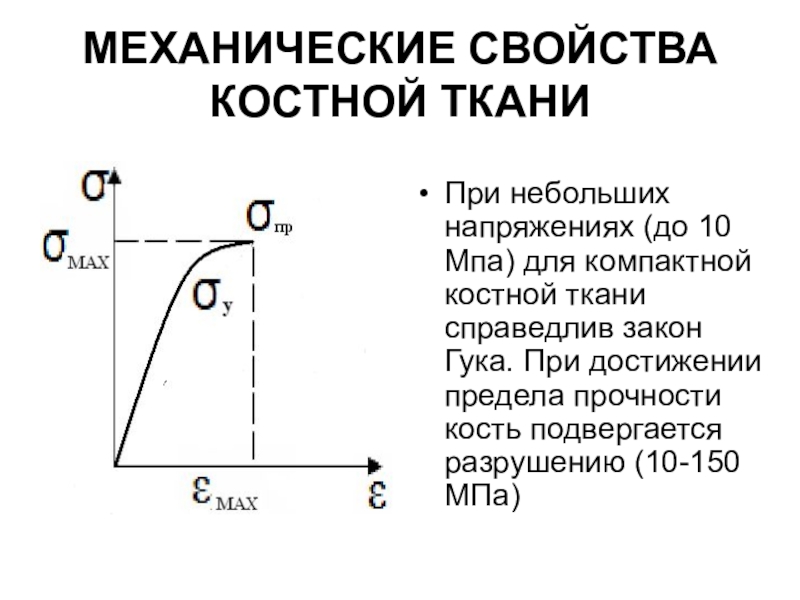
Прочность — свойство материала сопротивляться разрушению под действием внутренних напряжений, возникающих под воздействием внешних сил.

Относительное
удлинение



Закон Гука


Е – модуль Юнга

от природы материала, из которого изготовлен образец.
Коэффициент Пуассона и

модуль Юнга полностью характеризуют упругие свойства изотропного материала

предел упругости

- предел текучести

-

предел
прочности

Их предел прочности на разрыв оказывается малым по сравнению с

пределом прочности пластичных материалов.

гликопротеиды):
•Большая обратимая деформация (вязкоупругая)
Ползучесть
•Высокая прочность

Жидкости
•Неограниченная деформация

•Малая прочность

Твердые тела:
•Малая обратимая деформация
•Высокая прочность

вязкая жидкость может перетекать.
В момент t1 под действием

приложенной силы поршень перемещается, в момент t2 действие силы прекращается , но модель не возвращается в исходное состояние.

либо в
изотоническом режиме,
создавая определенное напряжение под действием постоянной

силы, и измеряя изменение со временем длины образца исследуемого материала, либо в изометрическом режиме,
проводя ступенчатое изменение длины образца и измерение в новом состоянии изменения напряжения со временем

системе возникает максимальное для заданной длины напряжение σ0 , которое

постепенно уменьшается по мере перемещения поршня (релаксация напряжения)

происходит практически мгновенное удлинение пружины и медленное перемещение поршня
Так на

этой модели реализуют свойство ползучести

растягивающих усилий
Напрягаются, проявляя свои слабые упругие свойства гладкие мышцы и

другие компоненты стенок полых органов
Напряжение их постепенно ослабевает благодаря деформации компонентов, обладающих вязкостными свойствами

Полые органы способны сильно растягиваться без развития напряжения

силы (т.е. создания постоянного напряжения) удлинение модели соответствует экспоненциальному закону.

Если удлинить модель на определенную величину, возникнет соответствующее напряжение, не меняющееся со временем.

компактной костной ткани справедлив закон Гука. При достижении предела прочности

кость подвергается разрушению (10-150 МПа)

модели прежде всего происходит удлинение пру жины 1, к которой

непосредственно приложена сила (участок ОА).
АВ – область ползучести – удлинение пружины 2 и одновременное перемещение поршня. В момент t 2 снимаем действующую силу
ВС – деформация сжатия за счет сокращения пружины 1 при снятии нагрузки

Реальная кривая модель

ОА - увеличение напряжения в модели при удлинении модели за счет растяжения пружины 1
AB – сокращение пружины 1 с одновре -менным вытягиванием поршня и растяжением пружины 2.-релаксация напряжения

моделью Зинера

ее стенок
Методика, позволяющая по записи колебаний артериальной стенки определить

скорость пульсовой волны и оценить механические свойства сосудистой стенки называется сфигмография

Е – модуль упругости
сосудистой стенки
h – толщина стенки сосуда
d- диаметр сосуда
ρ – плотность крови

скорость пульсовой волны

Гука для деформации удлинения-сжатия и деформации сдвига. Диаграмма растяжения.
3. Механические

(реологические) модели упруговязких свойств материалов (идеально упругий элемент, идеально вязкий элемент).Модель Максвелла. Модель Кельвина-Фойгта.
4.Механические свойства костной ткани. Модель Зинера
5.Механические свойства мышечной ткани
6.Механические свойства тканей кровеносных сосудов. 7.Пульсовая волна (механизм возникновения и скорость распространения