Слайд 1Числовые характеристики случайной величины
Лекция 2
Слайд 2Числовые характеристики
1. Характеристики положения случайной величины на числовой оси
(мода Мo, медиана Мe, математическое ожидание М(Х)).
2. Характеристики разброса случайной величины около
среднего значения (дисперсия D(X), среднее квадратическое отклонение σ(х)).
3. Характеристики формы кривой y = φ(x) (асимметрия As, эксцесс Ех).
Слайд 3Математическое ожидание
Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются
все возможные значения Х.
Для дискретной случайной величины, которая может принимать
лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений:
Для непрерывной случайной величины Х, имеющей заданную плотность распределения φ(x) математическим ожиданием называется следующий интеграл:
Слайд 4Свойства математического ожидания
1. М(С) = C, где С = const;
2. M(C∙Х) = С∙М(Х);
3. М(Х ± Y)
= М(Х) ± М(Y), где X и Y – любые случайные величины;
4. М(Х∙Y)=М(Х)∙М(Y), где X и Y – независимые
случайные величины.
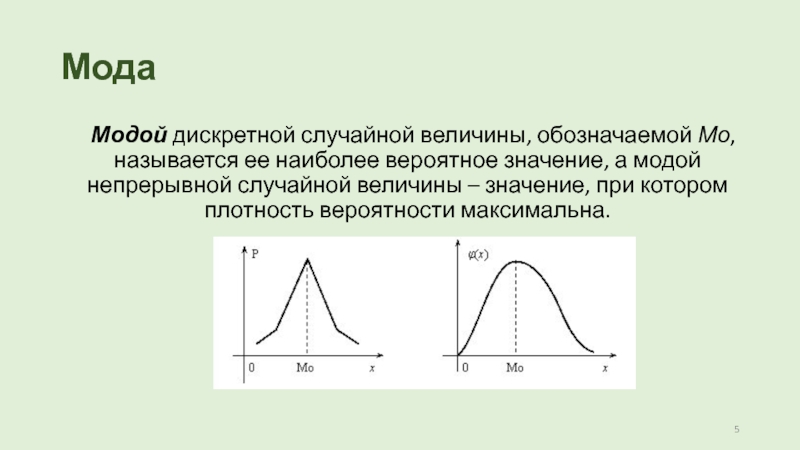
Слайд 5Мода
Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение, а
модой непрерывной случайной величины – значение, при котором плотность вероятности
максимальна.
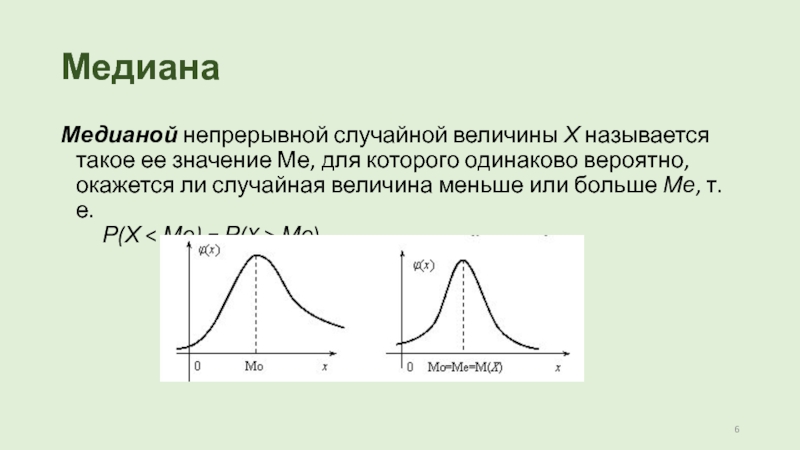
Слайд 6Медиана
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково
вероятно, окажется ли случайная величина меньше или больше Ме, т.е.
Р(Х
Р(X > Ме)
Слайд 7Дисперсия
Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического
ожидания
D(X) = M(X –М(Х))2.
Дисперсию случайной величины Х удобно вычислять по формуле:
а) для
дискретной величины
б) для непрерывной случайной величины
Дисперсия обладает следующими свойствами:
1. D(C) = 0, где С = const;
2. D(C×X) = C2∙D(X);
3. D(X±Y) = D(X) + D(Y), если X и Y независимые случайные величины.
Слайд 8Среднее квадратическое отклонение
Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии,
т.е.
σ(X) =
Слайд 9Моменты случайных величин
Начальным моментом k-го порядка αk случайной величины Х называется математическое ожидание величиныХk, т.е.
αk = М(Хk).
Начальный момент первого порядка – это математическое ожидание случайной
величины.
Центральным моментом k-го порядка μk случайной величины Х называется математическое ожидание величины (Х–М(Х))k, т.е. μk = М(Х–М(Х))k.
Центральный момент второго порядка – это дисперсия случайной величины.
Для дискретной случайной величины начальный момент выражается суммой αk = , а центральный – суммой μk= где рi = p(X = xi). Для начального и центрального моментов непрерывной случайной величины можно получить следующие равенства:
αk = , μk = ,
где φ(x) – плотность распределения случайной величины Х
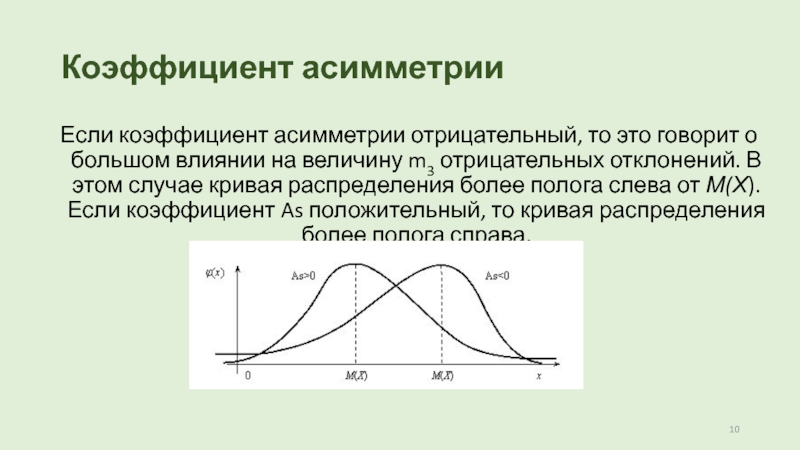
Слайд 10Коэффициент асимметрии
Если коэффициент асимметрии отрицательный, то это говорит о большом
влиянии на величину m3 отрицательных отклонений. В этом случае кривая распределения
более полога слева от М(Х). Если коэффициент As положительный, то кривая распределения более полога справа.
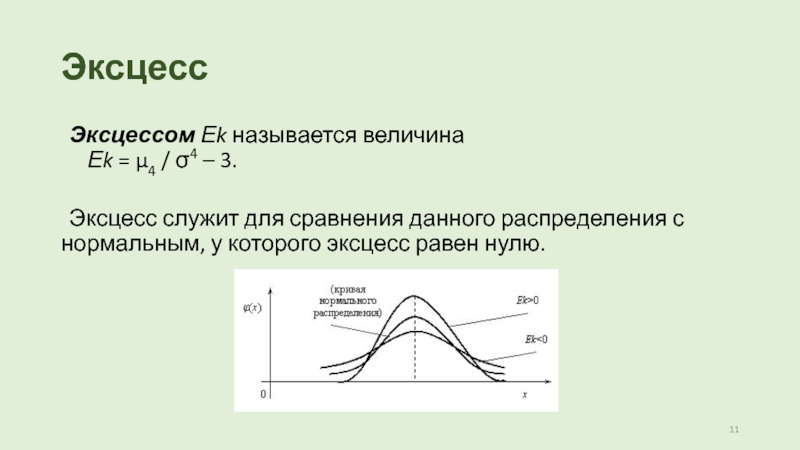
Слайд 11Эксцесс
Эксцессом Еk называется величина
Еk = μ4 / σ4 – 3.
Эксцесс служит для сравнения данного распределения
с нормальным, у которого эксцесс равен нулю.
Слайд 12Основные распределения дискретной случайной величины
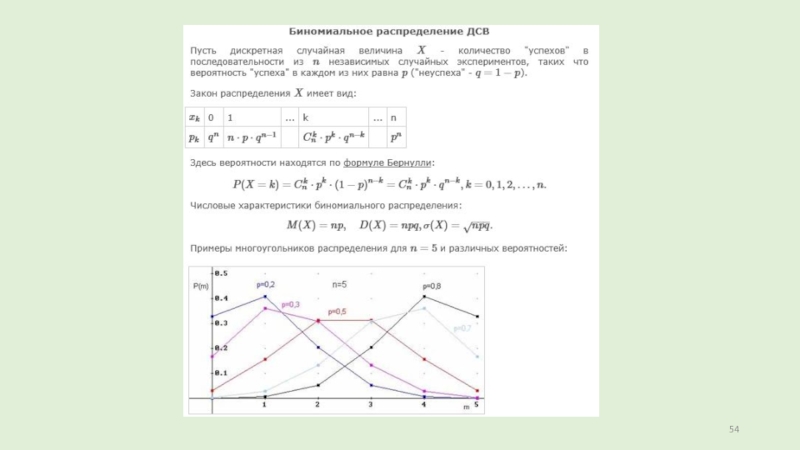
Слайд 13Биноминальное распределение
Пусть в каждом из n независимых испытаний событие А может произойти с одной
и той же вероятностью р(следовательно, вероятность непоявления q =1 – p).
Дискретная случайная величина Х –
число наступлений события А– имеет распределение, которое называется биномиальным.
Слайд 14Распределение Пуассона
Это распределение представляет собой предельный случай биномиального, когда вероятность р очень
мала, а число испытаний n велико.
Дискретная случайная величина Х, которая может
принимать только целые неотрицательные значения с вероятностями
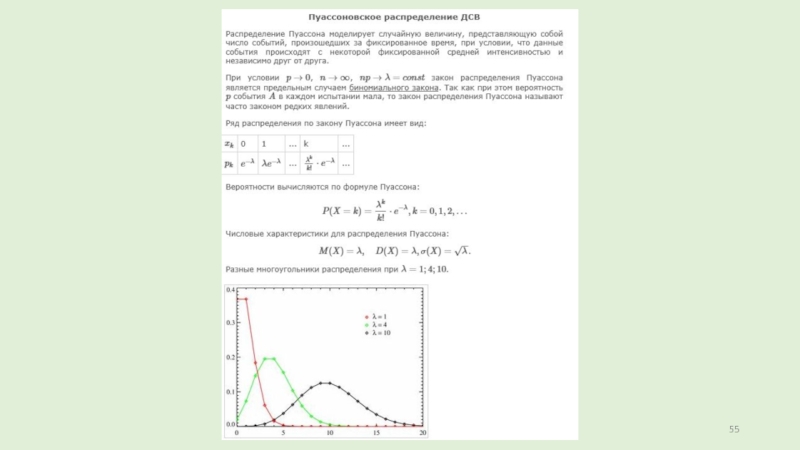
Слайд 15Распределение Пуассона
Закон Пуассона описывает число событий k, происходящих за одинаковые
промежутки времени. При этом полагается, что события появляются независимо друг
от друга с постоянной средней интенсивностью, которая характеризуется параметром λ = n·p
По распределению Пуассона распределено, например число посетителей магазина или банка за определенный промежуток времени, при этом λ – среднее число посетителей за это время.
Предположим, что в среднем в магазин приходит 2,1 покупатель в минуту. Тогда,
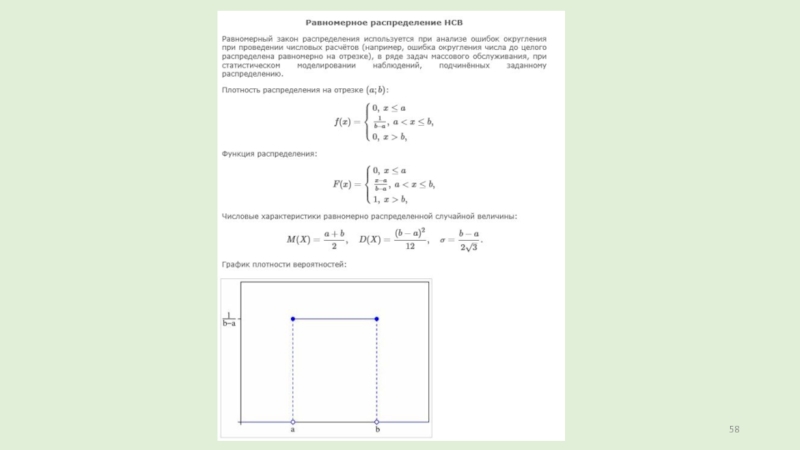
Слайд 16Равномерное распределение
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если
ее плотность имеет следующий вид:
График плотности распределения
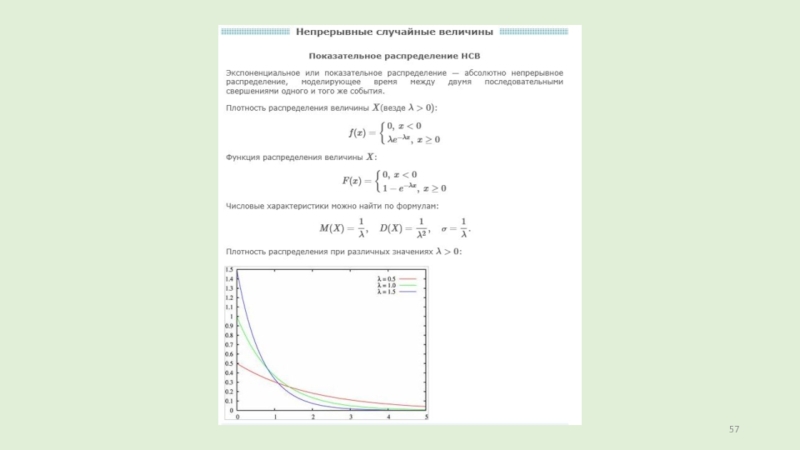
Слайд 17Показательное распределение
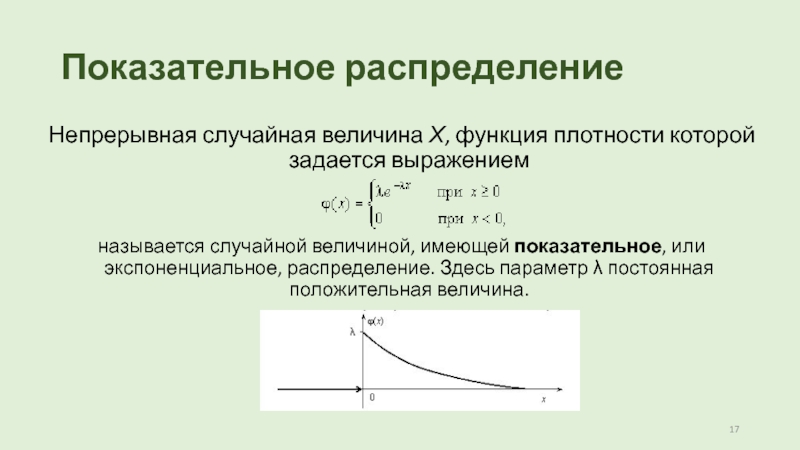
Непрерывная случайная величина Х, функция плотности которой задается выражением
называется случайной
величиной, имеющей показательное, или экспоненциальное, распределение. Здесь параметр λ постоянная положительная
величина.
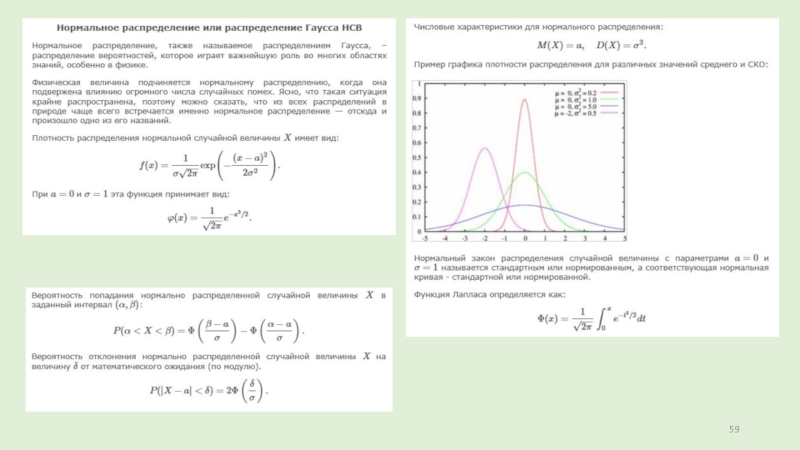
Слайд 18Нормальное распределение
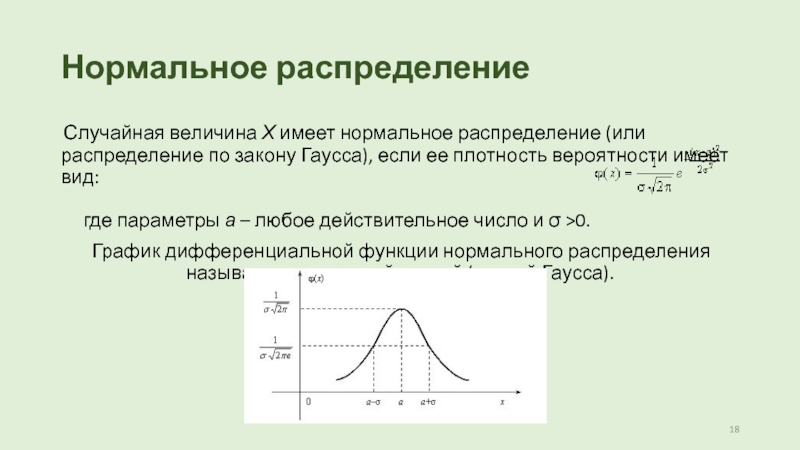
Случайная величина Х имеет нормальное распределение (или распределение по закону Гаусса),
если ее плотность вероятности имеет вид:
где параметры а – любое действительное
число и σ >0.
График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса).
Слайд 20Решение задачи на классическую вероятность
Абонент забыл последние 2 цифры телефонного
номера, но помнит, что они различны и образуют двузначное число,
меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.
Слайд 21Решение задачи на классическую вероятность
Абонент забыл последние 2 цифры телефонного
номера, но помнит, что они различны и образуют двузначное число,
меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.
Решение: подсчитаем количество всех возможных двузначных чисел с разными цифрами, меньшее 30, которые может набрать абонент:
Ответ: 1/18.
Слайд 22Схема Бернулли
Из n аккумуляторов за год хранения k выходит из
строя. Наудачу выбирают m аккумуляторов. Определить вероятность того, что среди
них l исправных.
n=100, k=7,m=5, l=3
Слайд 23Схема Бернулли
Из n аккумуляторов за год хранения k выходит из
строя. Наудачу выбирают m аккумуляторов. Определить вероятность того, что среди
них l исправных.
n=100, k=7,m=5, l=3
Решение: Имеем схему Бернулли с параметрами p=7/100=0,07 (вероятность того, что аккумулятор выйдет из строя), n=5 (число испытаний), k=5−3=2 (число «успехов», неисправных аккумуляторов).
Получаем
Ответ: 0,0394.
Слайд 24Теоремы сложения и умножения вероятностей
Задача: трое учащихся на экзамене независимо
друг от друга решают одну и ту же задачу. Вероятности
ее решения этими учащимися равны 0,8, 0,7 и 0,6 соответственно. Найдите вероятность того, что хотя бы один учащийся решит задачу.
Слайд 25Теоремы сложения и умножения вероятностей
Слайд 26Формула полной вероятности
Задача. Из 1000 ламп 380 принадлежат к 1
партии, 270 – ко второй партии, остальные к третьей. В
первой партии 4% брака, во второй - 3%, в третьей – 6%. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа – бракованная.
Слайд 28Формула Байеса
Задача. Из 30 стрелков 12 попадает в цель с
вероятностью 0.6, 8 - с вероятностью 0.5 и 10 –
с вероятностью 0.7. Наудачу выбранный стрелок произвел выстрел, поразив цель. К какой из групп вероятнее всего принадлежал этот стрелок?
Слайд 31Биноминальный закон распределения
Задача. В городе 4 коммерческих банка. У каждого
риск банкротства в течение года составляет 20%. Составьте ряд распределения
числа банков, которые могут обанкротиться в течение следующего года.
Слайд 32Биноминальный закон распределения
Слайд 33Закон распределения Пуассона
Задача. Среднее число самолетов, взлетающих с полевого аэродрома
за одни сутки, равно 10. Найти вероятность того, что за
6 часов взлетят:
А) три самолета,
Б) не менее двух самолетов
Слайд 35Примеры решения задач по математической статистике
Слайд 36Простой вариационный ряд
Задача 1. Дан следующий вариационный ряд
1 2
3 4 5 6 7 8 9 10
1 1 2
2 4 4 4 5 5 5
Требуется
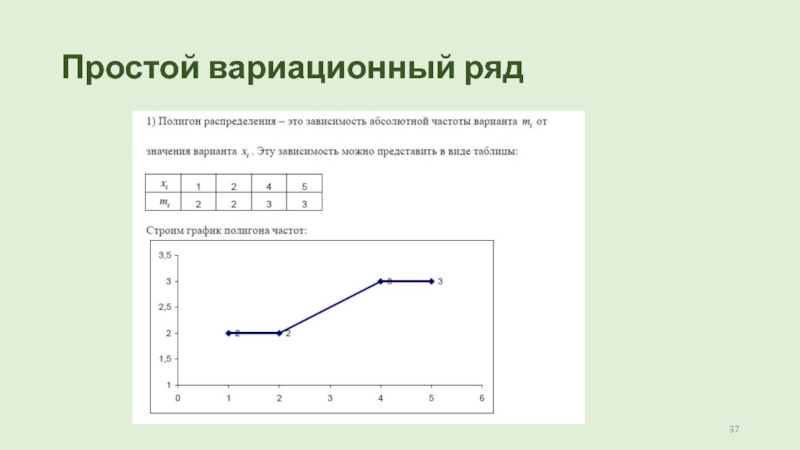
1) Построить полигон распределения
2) Вычислить выборочную среднюю, дисперсию, моду, медиану.
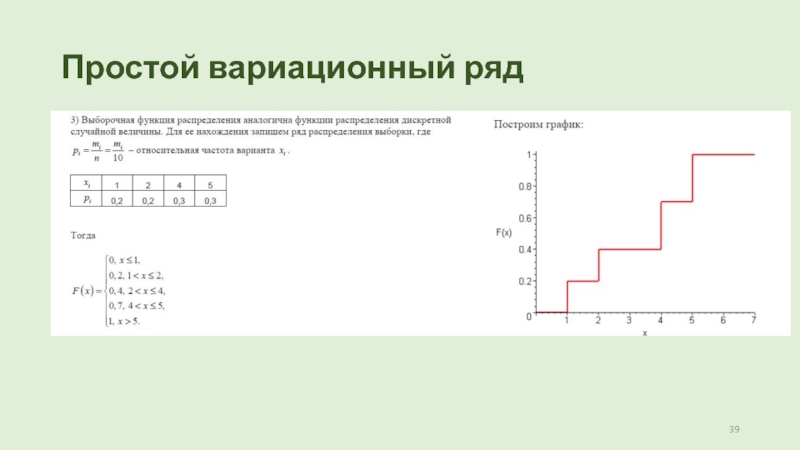
3) Построить выборочную функцию распределения
4) Найти несмещенные оценки математического ожидания и дисперсии.
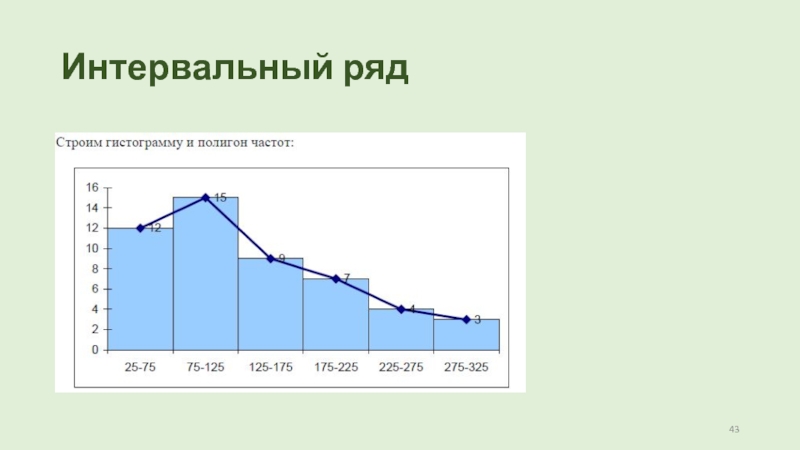
Слайд 41Интервальный ряд
Задача. Проведено выборочное обследование магазинов города. Имеются следующие данные
о величине товарооборота для 50 магазинов города (xi – товарооборот,
млн. руб.; ni – число магазинов).
xi 25-75 75-125 125-175 175-225 225-275 275-325
ni 12 15 9 7 4 3
Найти
а) среднее, среднее квадратическое отклонение S и коэффициент V;
б) построить гистограмму и полигон частот.
Слайд 44Задачи на построение доверительных интервалов
Строительная компания хочет оценить среднюю стоимость
ремонтных работ, выполняемых для клиентов. Каким должен быть объем выборки
среди 1200 клиентов строительной фирмы, если среднее квадратическое отклонение по результатам пробного обследования составило 850 у.е., а предельная ошибка выборки не должна превышать 200 у.е. с вероятностью 0,95?
Слайд 45Задачи на построение доверительных интервалов
Слайд 46Задачи на построение доверительных интервалов
С целью размещения рекламы опрошено 420
телезрителей, из которых данную передачу смотрят 170 человек. С доверительной
вероятностью 0,91 найти долю телезрителей, охваченных рекламой в лучшем случае
Слайд 47Задачи на построение доверительных интервалов
С целью размещения рекламы опрошено 420
телезрителей, из которых данную передачу смотрят 170 человек. С доверительной
вероятностью 0,91 найти долю телезрителей, охваченных рекламой в лучшем случае











![Числовые характеристики случайной величины Равномерное распределениеНепрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если ее Равномерное распределениеНепрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если ее плотность имеет следующий вид:График плотности распределения](/img/thumbs/e8a52da29cead7a7fae4a08d4fa75c47-800x.jpg)