Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Действия над числами в произвольной системе счисления 1
Содержание
- 1. Действия над числами в произвольной системе счисления 1
- 2. Cq = Aq +BqAq = an*qn+an-1*qn-1+…+a1*q1+a0*q0Bq = bm*qm+bm-1*qm-1+…+b1*q1+b0*q0Промежуточная сумма:si = ai + bi + pi-1Результат:
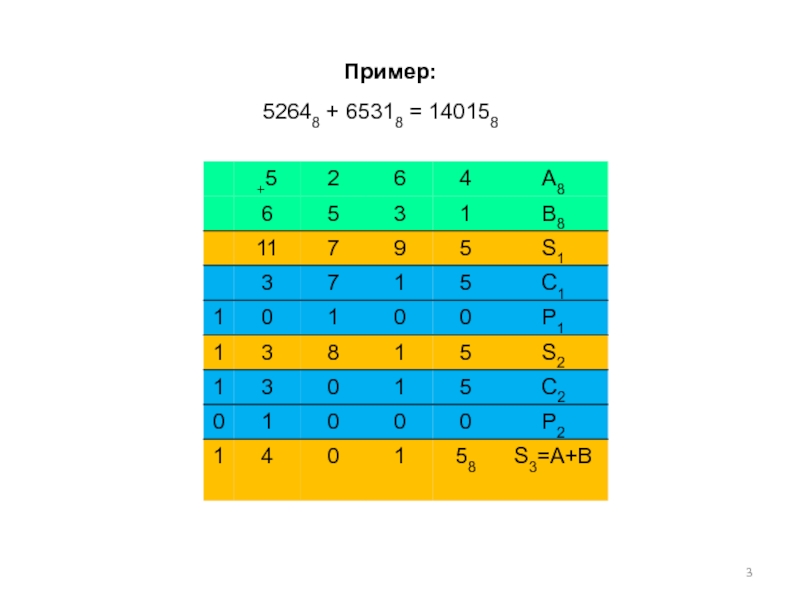
- 3. Пример:52648 + 65318 = 140158
- 4. Перевод чисел из одной системы счисления в
- 5. Перевод целых чисел:Способ 1. Для перевода целых
- 6. Обоснование способа 1:Ap = an*pn+an-1*pn-1+…+a1*p1+a0*p0Bq = br*qr+br-1*qr-1+…+b1*q1+b0*q0
- 7. Способ 2. Цифры и основание исходного представления
- 8. Способ 3. (модификация способа 2 с вычисление
- 9. Перевод правильных дробейПри переводе правильных дробей из
- 10. Количество разрядов в новом представлении дроби определяется
- 11. Пример. Перевести правильную дробь 0,3024 из 4-й
- 12. Перевод чисел из p-ичной системы счисления в
- 13. Перевод чисел, представленных в 2k-ичных системах счисления.Пример
- 14. Скачать презентанцию
Cq = Aq +BqAq = an*qn+an-1*qn-1+…+a1*q1+a0*q0Bq = bm*qm+bm-1*qm-1+…+b1*q1+b0*q0Промежуточная сумма:si = ai + bi + pi-1Результат:
Слайды и текст этой презентации
Слайд 2Cq = Aq +Bq
Aq = an*qn+an-1*qn-1+…+a1*q1+a0*q0
Bq = bm*qm+bm-1*qm-1+…+b1*q1+b0*q0
Промежуточная сумма:
si =
ai + bi + pi-1
Слайд 4Перевод чисел из одной системы счисления в другую
Постановка задачи. Представить
в q-ой СС смешанное число А, заданное в p-ой СС:
Ap
= an*pn+an-1*pn-1+…+a1*p1+a0*p0+a-1*p-1+a-2*p-2+…+a-m*p-mBq = br*qr+br-1*qr-1+…+b1*q1+b0*q0+b-1*q-1+b-2*q-2+…+b-s*q-s
Для смешанного числа отдельно проводится перевод целой и дробной частей.
Слайд 5Перевод целых чисел:
Способ 1. Для перевода целых чисел из p-ичной
СС в q-ичную необходимо исходное p‑ичное число и получаемые частные
последовательно делить на основание q новой СС. Получаемые в результате остатки представляют собой p-ичные записи q-ичных цифр числа, начиная с младшей. Операция деления проводится в p-ичной СС.Слайд 6Обоснование способа 1:
Ap = an*pn+an-1*pn-1+…+a1*p1+a0*p0
Bq = br*qr+br-1*qr-1+…+b1*q1+b0*q0
Aq /q =
{А1,S1}, где А1- целая часть результата, S1-остаток.
Bq /q = {В1,R1},
где B1- целая часть результата, R1-остаток.B1= br*qr-1+br-1*qr-2+…+b1*q0
R1 = b0
Т.к. Ap ≡ Bq, то b0 = S1.
Слайд 7Способ 2. Цифры и основание исходного представления числа в p-ой
СС выражаются q‑ичными числами и производится вычисление полученного выражения в
q-ичной СС.Ap = an*pn+an-1*pn-1+…+a1*p1+a0*p0 = = aqn*pqn+aqn-1*pqn-1+…+aq1*pq1+aq0*pq0
Пример. Перевести в 3-ю СС число 524, представленное в 7-й СС.
5247 = 5•72+2 •71+4 •70 =(12 •21 • 21+2 •21 +11)3 = 1002023
При вычислениях учитываем, что 57 = 123 ; 27 =23 ; 47 = 113
Слайд 8Способ 3. (модификация способа 2 с вычисление многочлена по схеме
Горнера). Цифры и основание исходного представления числа в p-ой СС
выражаются q‑ичными числами. В q‑ичной СС выполняются следующие операции:умножить старшую цифру на p;
добавить к результату следующую по порядку цифру;
умножить результат на p;
повторить операции 2 и 3 до тех пор, пока не будет добавлена младшая цифра; на последнем шаге операция умножения результата на p не проводится.
Такой подход позволяет, в общем случае, сократить при переводе количество операций умножения, которые выполняются гораздо дольше операций сложения.
5247 = 5•72+2 •71+4 •70 =(12 •21 • 21+2 •21+11)3 =
= ((12 •21 +2) •21+11)3 = 1002023
Слайд 9Перевод правильных дробей
При переводе правильных дробей из p-ичной СС в
q-ичную необходимо в p‑ичной СС выполнить следующие операции:
умножить исходное число
на q. Целая часть полученного результата является старшей цифрой числа в q-ичной СС;умножить дробную часть полученного результата на q. Целая часть полученного результата является очередной цифрой числа в q-ичной СС;
повторить операцию 2, пока не будет достигнута необходимая точность.
Слайд 10Количество разрядов в новом представлении дроби определяется абсолютной погрешностью исходного
и нового представления числа:
0,5•q-s ≤ 0,5•p-m
Слайд 11Пример. Перевести правильную дробь 0,3024 из 4-й в 7-ю систему
счисления.
Количество разрядов в новом представлении дроби:
n7 ≥ (n4 * ln
4) / ln 7 =2,137...n7 = 2
Для получения 2-х цифр в окончательном результате необходимо выполнять процесс умножения до получения 3-х цифр нового представления дроби и провести округление:
x0,3024
134 ; =7
+2112
3020
11.132
x 0,132
13
+1122
1320
3.102
x0.102
13
+312
1020
0,1332
Таким образом, 0,3024 = 0,530…7 ≈ 0,537,
Слайд 12Перевод чисел из p-ичной системы счисления в q-ичную при p
= qk
Перевод целых чисел.
При переводе целых чисел из p-ичной
СС в q-ичную необходимо каждую цифру исходного p-ичного числа заменить ее k-разрядным q-ичным эквивалентом.Перевод правильных дробей.
При переводе правильных дробей из p-ичной СС в q-ичную необходимо каждую цифру исходного p-ичного числа заменить ее k-разрядным q-ичным эквивалентом.
Перевод чисел из p-ичной системы счисления в q-ичную при q = p k
Перевод целых чисел.
При переводе целых чисел из p-ичной СС в q-ичную необходимо исходное p‑ичное число разбить на группы по k разрядов, начиная справа, и каждую группу заменить одной q-ичной цифрой. При необходимости старшая группа дополняется слева нулями до k разрядов.
Перевод правильных дробей.
При переводе правильных дробей из p-ичной СС в q-ичную необходимо исходное p‑ичное число разбить на группы по k разрядов, начиная слева, и каждую группу заменить одной q-ичной цифрой. При необходимости младшая группа дополняется справа нулями до k разрядов.
Слайд 13Перевод чисел, представленных в 2k-ичных системах счисления.
Пример 1. Перевести число
571,45 из 8-й в 2-ю систему счисления.
Так как 8 =
23, то каждую 8-ричную цифру необходимо заменить ее 3-х разрядным двоичным эквивалентом:571,458 = 101 111 001, 100 1012.
Пример 2. Перевести число 10111011001,1011012 из 2-й в 16-ю CC.
Так как 16 = 24, то исходное число необходимо разбить на группы по 4 разряда, при этом придется дополнить старшую группу целой части числа двумя нулями слева, а младшую группу дробной части нулем справа:
0010 1101 1001,1011 00102 = 2D9,B216
Пример 3. Перевести число E4,57 из 16-й в 8-ю систему счисления.
Так как 16 ≠ 8k, то прямой перевод по упрощенным правилам невозможен. В этом случае необходимо либо воспользоваться правилами переводав произвольных СС, либо выполнить промежуточныый перевод в 2-ю СС, так как 8=23 и 16=24: Воспользуемся вторым подходом.
E4,5716 = 1110 0100,0101 01112 = 011 100 100,010 101 1102 = 344,2568