Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дискретная математика
Содержание
- 1. Дискретная математика
- 2. РазделыМножества и отношенияАлгебраические структурыТеория графов и ее приложенияТеория кодирования Математическая логикаТеория автоматовТеория формальных грамматик Теория алгоритмов
- 3. Слайд 3
- 4. ЛитератураНовиков Ф.А. Дискретная математика для программистов. —
- 5. Теория множеств
- 6. Персоналии Основные положения
- 7. Интуитивное понятие множества Г.Кантора «Произвольная
- 8. МОЩНОСТЬЮ (или КАРДИНАЛЬНЫМ ЧИСЛОМ) множества называется количество
- 9. Отношения между множествамиДва множества A и B
- 10. Способы задания множествПеречислением элементов, Описание характеристических свойств или характеристическим предикатом;Порождающей процедурой (например, индуктивными или рекурсивными правилами).
- 11. Парадокс. АнтиномияПарадокс — это два противоположных, несовместимых
- 12. Антиномии (парадоксы)Антиномия Рассела. Рассмотрим все множества, не
- 13. Операции над множествамиОБЪЕДИНЕНИЕМ (ДИЗЪЮНКЦИЕЙ, СУММОЙ) множеств A
- 14. Семейство множестваФиксируем множество Ω. Мы рассматриваем подмножества
- 15. Разбиения и покрытия множествЕсли множество A представляет
- 16. Законы алгебры множествЗаконы ассоциативностиЗаконы коммутативностиЗаконы тождестваЗаконы идемпотентностиЗаконы дистрибутивностиЗаконы дополненияЗаконы де Моргана
- 17. Слайд 17
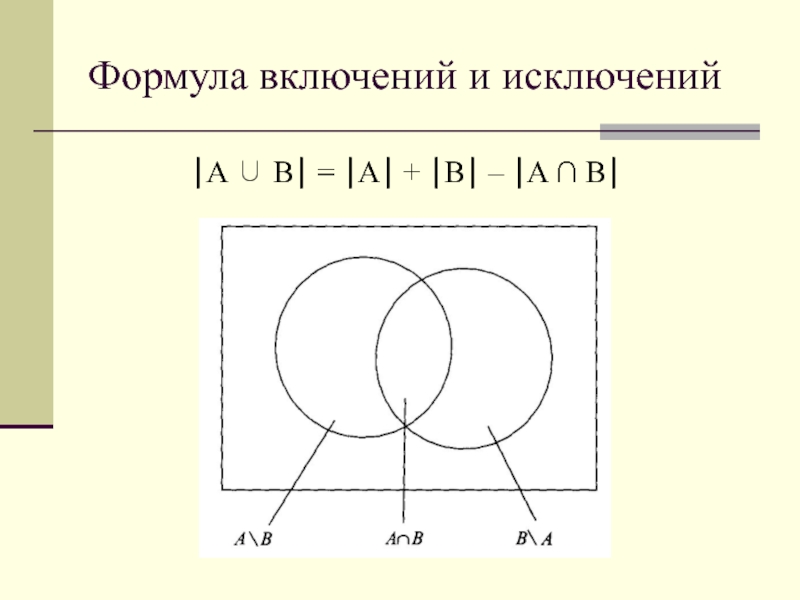
- 18. Формула включений и исключенийA B = A + B – A B
- 19. Соответствия и отношения
- 20. Упорядоченной парой
- 21. Декартовым произведением произвольного числа множеств А1, А2,
- 22. СООТВЕТСТВИЕ, бинарное отношение между двумя множествами A
- 23. Области определения и значения соответствия R A
- 24. Образы и прообразы элементов Образ a
- 25. Свойства соответствий R A BВсюду (полностью) определенное
- 26. Соответствие F, заданное на множествах A1,
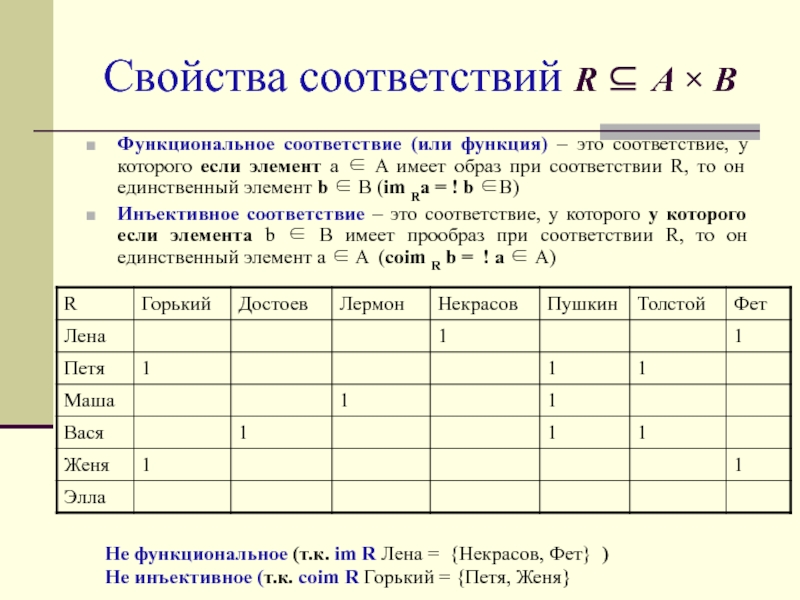
- 27. Свойства соответствий R A BФункциональное соответствие (или
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Разделы
Множества и отношения
Алгебраические структуры
Теория графов и ее приложения
Теория кодирования
Математическая
логика
Слайд 3 Оценка по курсу: 60%
— семинары, 40% — ответ на экзамене
Итоговая оценка
От 40
до 64 баллов — 3От 65 до 84 баллов — 4
85 баллов и выше — 5
Семинары — самостоятельные работы, компьютерные работы, активность, индивидуальные творческие задания
Экзамен — 3 вопроса (до 10 баллов каждый), в случае «пограничного» количества баллов по Вашему желанию может быть дать дополнительный вопрос (От 0 до 10 балов)
Слайд 4Литература
Новиков Ф.А. Дискретная математика для программистов. — СПб: Питер, 2000
Лавров
И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и
теории алгоритмов. – M.: Физматлит, 1995.Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. — М.: Энергоатомиздат, 1988
Липский В. Комбинаторика для программистов. — М.: Мир, 1988
Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. — М.: Логос, 2000
Слайд 6Персоналии
Основные положения теории множеств были
разработаны
Бернардом Больцано (1781 – 1848)
Рихардом Дедекиндом (1831 – 1916)
Георгом Кантором
(1845 – 1918)Дальнейшее развитие
Альфред Норт Уайтхед (1861 – 1947)
Лейтзен Эгберт Ян Брауэр (1881 – 1966)
Герман Вейль (1885 – 1955)
Хаскелл Брукс Карри (1900 - )
Бертран Рассел (1872 – 1970)
Слайд 7Интуитивное понятие множества Г.Кантора
«Произвольная совокупность определенных предметов
нашей интуиции или интеллекта, которые можно отличить один от другого
и которые представляются как единое целое, называется множеством. Предметы, которые входят в состав множества, называются его элементами»Через обозначается отношение принадлежности, т.е. x A означает, что элемент x принадлежит множеству A.
Если x не является элементом множества A, то это записывается x A или x A.
Слайд 8МОЩНОСТЬЮ (или КАРДИНАЛЬНЫМ ЧИСЛОМ) множества называется количество элементов в нем.
Множества
с одинаковыми кардинальными числами называются эквивалентными.
Множества могут быть конечными (т.е.
состоящими из конечного числа элементов) и бесконечными.Множество мощности 0, не содержащее элементов, называется пустым и обозначается через .
Некоторое, общее для всех множеств данной мощности, надмножество, называется универсальным множеством или УНИВЕРСУМОМ и обозначается обычно как U.
Слайд 9Отношения между множествами
Два множества A и B считаются равными, если
они состоят из одних и тех же элементов (интуитивный принцип
объемности). Пишется A = B, если A и B равны, и A B в противном случае.Через обозначается ОТНОШЕНИЕ ВКЛЮЧЕНИЯ множеств, т.е. A B означает, что каждый элемент множества A является элементом множества B. В этом случае A называется ПОДМНОЖЕСТВОМ B, а B — НАДМНОЖЕСТВОМ A. Если A B и A B, то A называется СОБСТВЕННЫМ ПОДМНОЖЕСТВОМ B, и в этом случае пишем A B.
Слайд 10Способы задания множеств
Перечислением элементов,
Описание характеристических свойств или характеристическим предикатом;
Порождающей
процедурой (например, индуктивными или рекурсивными правилами).
Слайд 11Парадокс. Антиномия
Парадокс — это два противоположных, несовместимых утверждения, для каждого
из которых имеются кажущиеся убедительными аргументы
Наиболее резкая форма парадокса —
антиномия, рассуждение, доказывающее эквивалентность двух утверждений, одно из которых является отрицанием другого.Слайд 12Антиномии (парадоксы)
Антиномия Рассела. Рассмотрим все множества, не содержащие самих себя.
Рассмотрим множество всех таких множеств. Тогда: если оно не содержит
себя, то оно содержит себяАнтиномия всемогущества. Бог всемогущ, поэтому он может создать такой камень, который сам не сможет поднять. Но Бог всемогущ, поэтому он может поднять любой камень.
Парадокс «Деревенский парикмахер»
Слайд 13Операции над множествами
ОБЪЕДИНЕНИЕМ (ДИЗЪЮНКЦИЕЙ, СУММОЙ) множеств A и B называется
множество
A B = {x x A или x B}.
ПЕРЕСЕЧЕНИЕМ (КОНЪЮНКЦИЕЙ) множеств A и B называется множество
A B = {x x A
и x B}.РАЗНОСТЬЮ множеств A и B называется множество
A \ B = {x x A и x B}
Разность U \ A называется ДОПОЛНЕНИЕМ множества A и обозначается через –A.
СИММЕТРИЧЕСКОЙ РАЗНОСТЬЮ множеств A и B называется множество
A B = (A \ B) (B \ A)
Слайд 14Семейство множества
Фиксируем множество Ω. Мы рассматриваем подмножества Ω, т.е. множества,
содержащиеся в Ω. Семейство подмножеств Ω обозначаем через P(Ω); P(Ω)
— множество, все элементы которого сами являются множествами. Термин семейство понимается здесь в следующем смысле: семейство — множество, все элементы которого сами являются множествами (вместо множество множеств говорим семейство множеств).Булеан множества — множество всех подмножеств множества
Слайд 15Разбиения и покрытия множеств
Если множество A представляет собой объединение подмножеств
А1, А2, …, Аn, …, то совокупность {А1, А2, …,
Аn, …} подмножеств называется покрытием множества A.Если же совокупность подмножеств покрытия множества A такова, что Ai Aj = при i j, то совокупность {А1, А2, …, Аn, …} называется разбиением множества A, а подмножества Ai — классами этого разбиения.
Слайд 16Законы алгебры множеств
Законы ассоциативности
Законы коммутативности
Законы тождества
Законы идемпотентности
Законы дистрибутивности
Законы дополнения
Законы де
Моргана
Слайд 20 Упорядоченной парой называется запись вида
(a, b), где a — элемент A , а b
— элемент B.Декартово или прямое произведение множеств A и B — A B — множество всех таких упорядоченных пар элементов этих множеств.
Декартово (прямое) произведение множеств
Слайд 21Декартовым произведением произвольного числа множеств А1, А2, …, An называется
множество
А1 А2 … An = {(а1,
а2, ..., ап) : аi Аi, i = 1, 2, ...,n}. Если А1 = А2 =…= An = А, то А А … A = An
Слайд 22СООТВЕТСТВИЕ, бинарное отношение между двумя множествами A и B —
произвольное подмножество R декартова произведения A B.
Если a
A, b B и (a, b) R, то пишут также R(a, b) или aRb. Если R = — пустое множество, то соответствие называется пустым, а если R = A B, то соответствие называется полным.Пусть R A B. Областью определения Dom R называется множество элементов a A, для каждого из которых найдется хотя бы один элемент b B такой, что aRb. Областью значений, или образом, Im R соответствия R называется множество элементов b B, для каждого из которых найдется хотя бы один элемент a A такой, что aRb. Соответствие R называется всюду определенным, если Dom R = A, и сюръективным, если Im R = B.
Для каждого a A множество элементов b B таких, что aRb, называется образом a относительно R и обозначается im R a. Прообразом элемента b B относительно R называется множество элементов a A таких, что aRb; прообраз обозначается coim R b. Ясно, что
Im R = a A im R a, Dom R = b B coim R b.
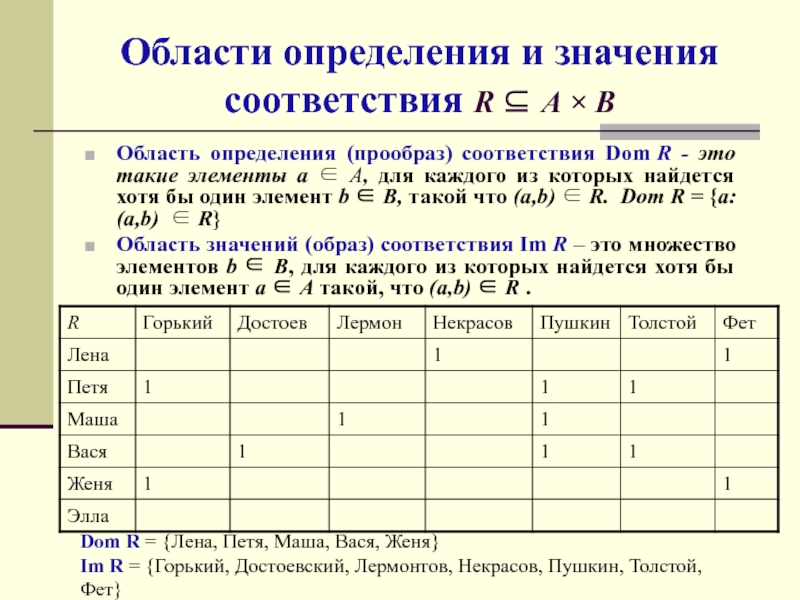
Слайд 23Области определения и значения
соответствия R A B
Область определения (прообраз) соответствия
Dom R - это такие элементы а A, для каждого
из которых найдется хотя бы один элемент b B, такой что (a,b) R. Dom R = {a: (a,b) R}Область значений (образ) соответствия Im R – это множество элементов b B, для каждого из которых найдется хотя бы один элемент a A такой, что (a,b) R .
Dom R = {Лена, Петя, Маша, Вася, Женя}
Im R = {Горький, Достоевский, Лермонтов, Некрасов, Пушкин, Толстой, Фет}
Слайд 24Образы и прообразы
элементов
Образ a А относительно R
(im R a) – это множество элементов b B таких, что
(a,b) RПрообраз элемента b B относительно R (coim R b) – это множество элементов a A таких, что (a,b) R
Im R = a A im R a, Dom R = b B coim R b.
im R Лена = {Некрасов, Фет} coim R Горький = {Петя, Женя}
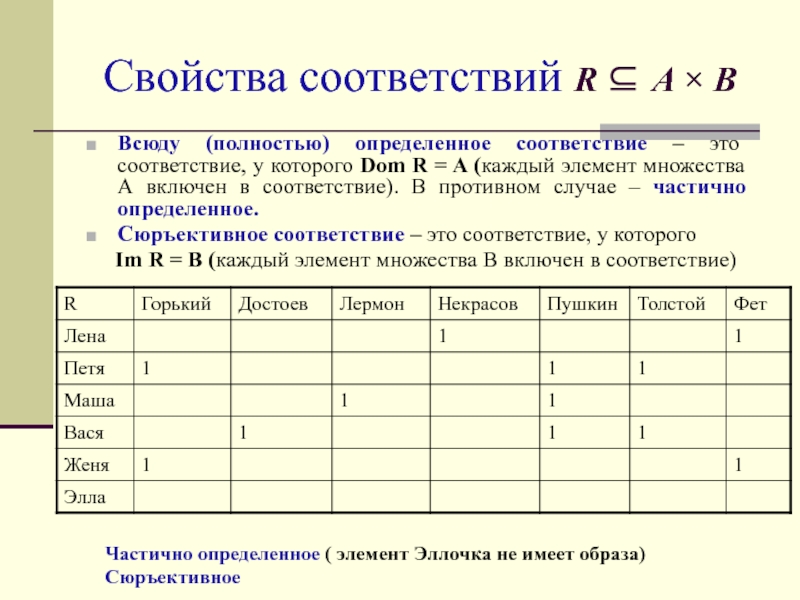
Слайд 25Свойства соответствий R A B
Всюду (полностью) определенное соответствие – это
соответствие, у которого Dom R = A (каждый элемент множества
А включен в соответствие). В противном случае – частично определенное.Сюръективное соответствие – это соответствие, у которого
Im R = B (каждый элемент множества В включен в соответствие)
Частично определенное ( элемент Эллочка не имеет образа)
Сюръективное
Слайд 26
Соответствие F, заданное на множествах A1, A2, …, An,
B называется функциональным, если для любого элемента (a1, a2, …,
an) из A1 A2 … An существует не более одного элемента b из B такого, что (a1, a2, …, an, b) F. Если такой элемент b из B существует для некоторого (a1, a2, …, an) , то он обозначается F(a1, a2, …, an) и записывается так: b = F(a1, a2, …, an) .В случае, если Dom(F) = A1 A2 … An , F называется полностью определенным, когда Dom(F) A1 A2 … An — частично определенным или просто частичным.
Соответствие F, заданное на множествах A1, A2, …, An, B называется отображением или функцией из A1 A2 … An в B (F: A1 A2 … An B), если F функциональное и полностью определенное. Соответствие F называется частичным отображением или частичной функцией, если F функциональное и частичное. Число n называют арностью функции F.
Функциональные соответствия
Слайд 27Свойства соответствий R A B
Функциональное соответствие (или функция) – это
соответствие, у которого если элемент a A имеет образ
при соответствии R, то он единственный элемент b B (im Ra = ! b B)Инъективное соответствие – это соответствие, у которого у которого если элемента b B имеет прообраз при соответствии R, то он единственный элемент a A (coim R b = ! a A)
Не функциональное (т.к. im R Лена = {Некрасов, Фет} )
Не инъективное (т.к. coim R Горький = {Петя, Женя}