это совокупность методов, основанных на изучении кинематических и динамических характеристик
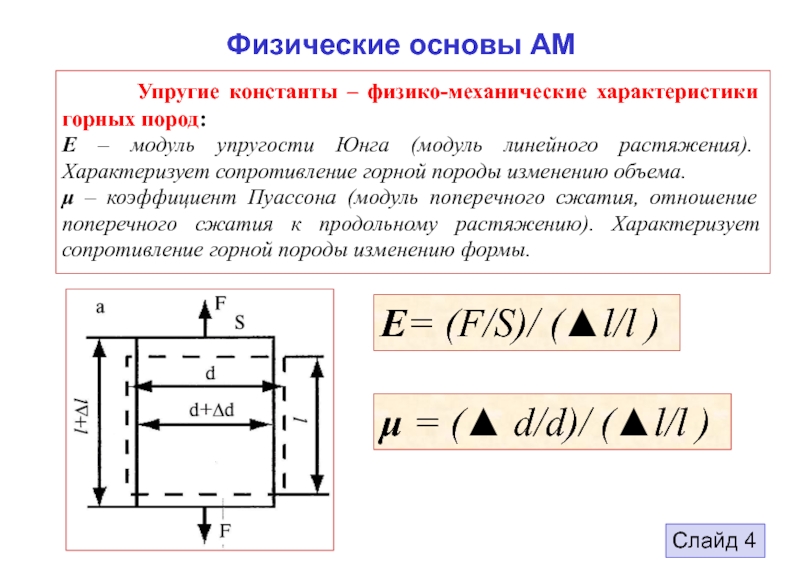
упругих волн (деформаций) , возбуждаемых в скважине импульсным источником. Горная порода рассматривается , в основном, как упругое тело. Упругое тело характеризуется тем, что при снятии приложенных сил, деформации восстанавливаются.
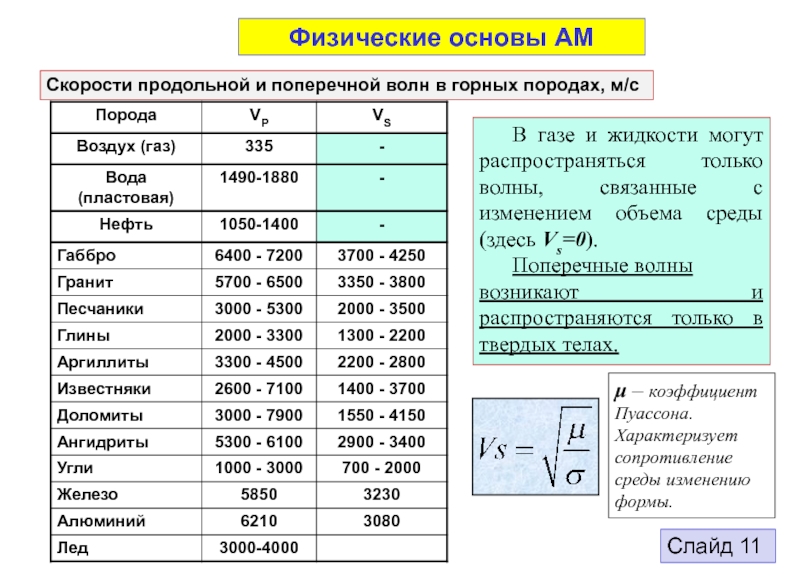
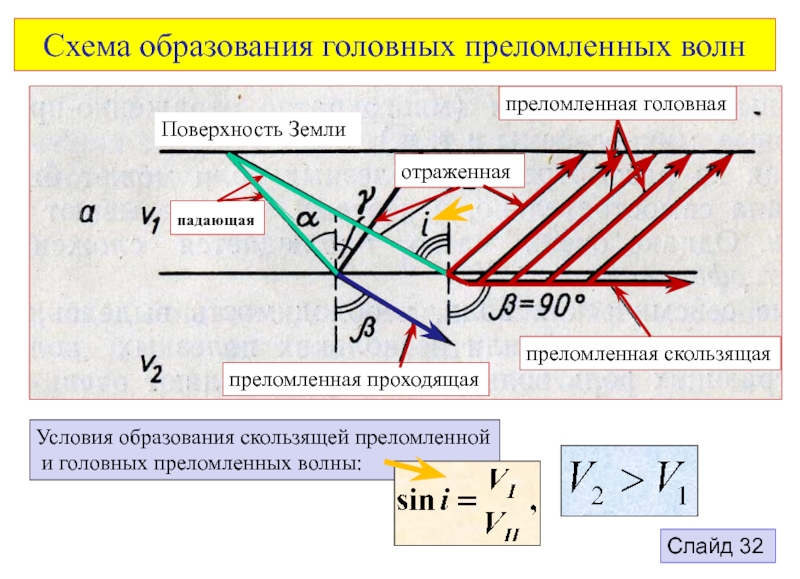
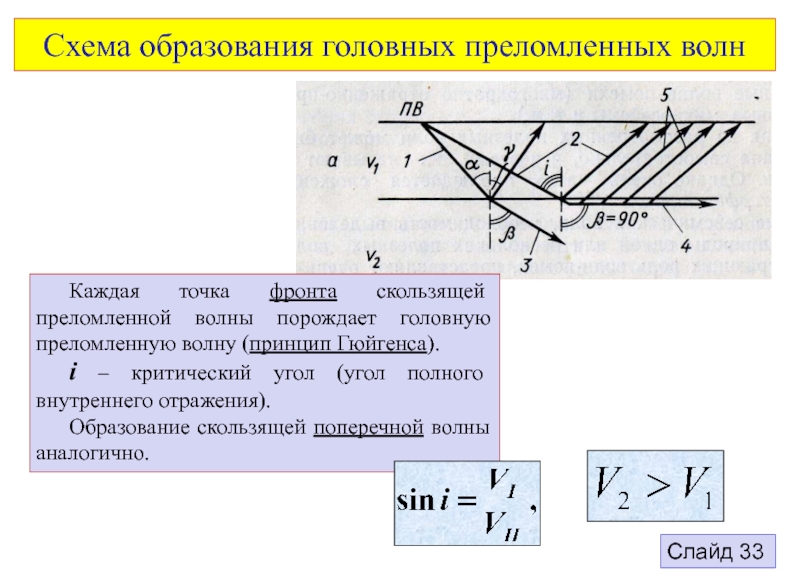
В однородной изотропной среде возникают и распространяются волны двух типов:
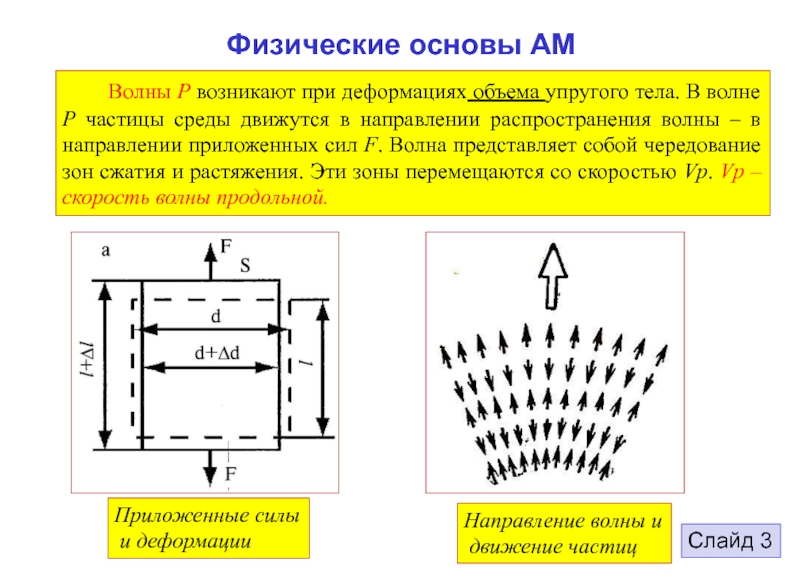
продольная волна – P-волна
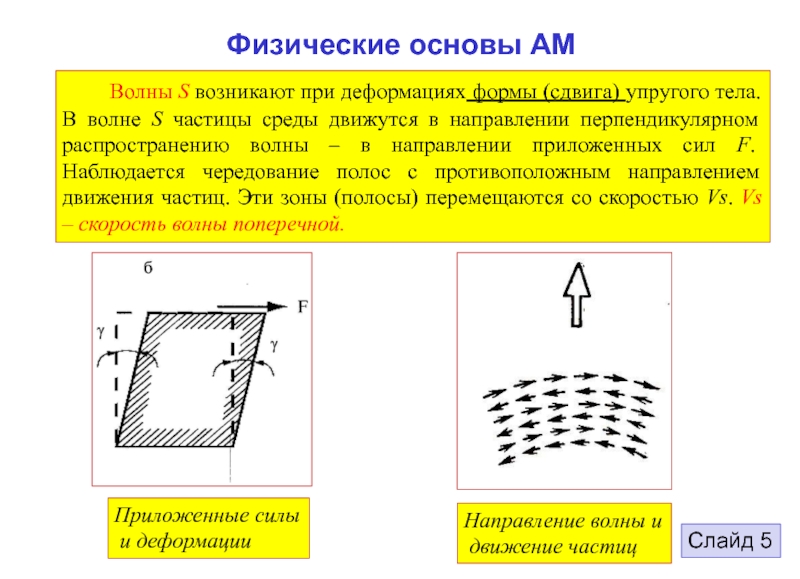
поперечная волна – S-волна
Слайд 2