ЭЛЕКТРОРАЗВЕДКА ЧАСТЬ 2

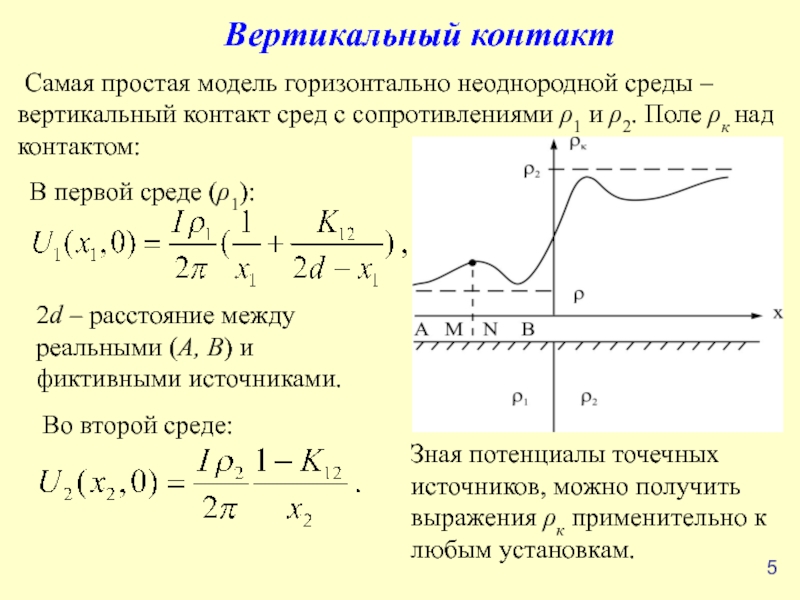
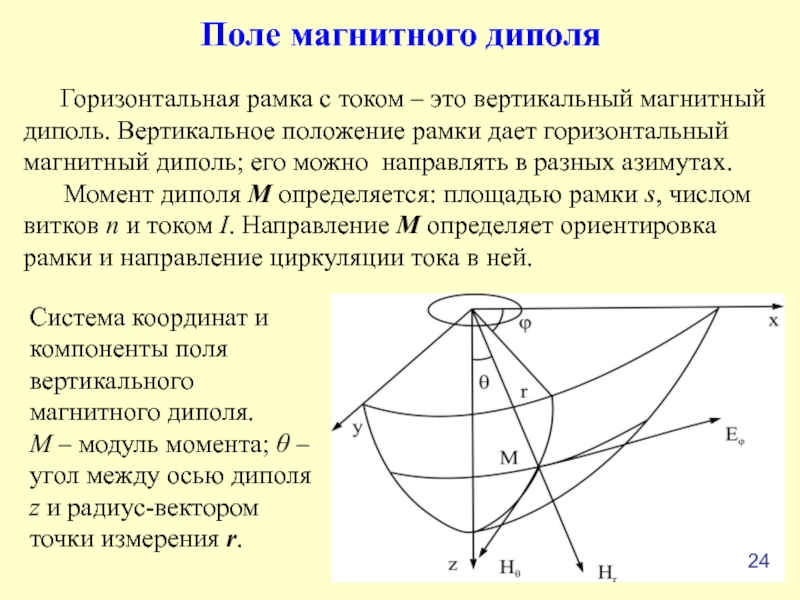
средой строится методом зеркальных отражений.
Фиктивные источники для вертикального контакта

(а)
и вертикального пласта (б)

Вводится фиктивный источник как отражение реального источника от границы раздела сред с разными сопротивлениями ρ1 и ρ2 (а). Если реальный источник тока I0 в среде ρ1, фиктивный – в ρ2, ток фиктивного источника в первой среде равен

рассмотрении поля в горизонтально-слоистой среде; в данном случае он называется

коэффициентом отражения поля границей раздела. Величина

называется коэффициентом прохождения электрического поля через границу. Очевидно, что коэффициенты отражения поля границей с разных сторон отличаются знаками: K21 = – K12. Очевидно соотношение:

В среде с сопротивлением ρ2, где нет реального источника, ток фиктивного источника определяется коэффициентом прохождения:

от границ и прохождение тока через границы. Очевидно возрастание числа

слагаемых токов от основных и фиктивных источников при увеличении числа границ.
Для прямой задачи это сложности технического порядка, однако при решении обратных задач нет смысла увеличивать число границ ввиду неоднозначности восстановления большого числа параметров (hi и ρi).
Потенциал в каждой среде Ui – сумма реального потенциала U0i , и потенциалов фиктивных источников Uфj :

Rj – расстояние точки определения потенциала Ui от j-го источника. В среде, где определяется потенциал, собственные фиктивные источники не учитываются.
Фиктивные источники нужны для учета искажающего влияния границ на поле в каждой части разреза.

контакт сред с сопротивлениями ρ1 и ρ2. Поле ρк над

контактом:

В первой среде (ρ1):

2d – расстояние между реальными (А, В) и фиктивными источниками.

Во второй среде:

Зная потенциалы точечных источников, можно получить выражения ρк применительно к любым установкам.

не очень велики. Ограничена и область применения методов количественной интерпретации

данных электроразведки.
Это зондирование и профилирование над одиночными или далеко отстоящие друг от друга (по сравнению с размерами установки) субвертикальные контакты, над отдельными включениями простой формы.
Для более сложных тел (по геометрии и распределению электропроводности) решение обратных задач в лучшем случае ограничивается приближенными оценками параметров по моделям простой формы.
Чаще это невозможно, и геологические выводы делаются на основе результатов качественной интерпретации данных электроразведки в сопоставлении с геологическими и другими геофизическими материалами.

Распространение электромагнитного поля описывается уравнениями Максвелла;

их дифференциальная форма:

B и D – магнитная индукция и электрическое смещение;
H и E  напряженность магнитного и электрического полей,
j  плотность тока проводимости,
q  плотность электрических зарядов.

Материальные уравнения связывают характеристики полей и свойства среды:

любой суммы полей уравнения Максвелла справедливы, если они верны для

каждого поля в отдельности.
Распространение электромагнитного поля вне его источников в зависимости от частоты и свойств среды
(, , ,) может носить волновой или диффузный характер. Скорость электромагнитных волн в среде v, в вакууме с:

В электромагнитной волне векторы E, H, и v (скорость волны) ортогональны и образуют правовинтовую систему. Изменения H (t) и E (t) синфазные.

В геофизике используются простые системы токов, чтобы неоднородности электромагнитных полей были связаны со средой, а не с интерференцией нормальных полей.

 = const,  = const,  = const, называется нормальным электромагнитным

полем.
Постоянные свойства среды можно вынести за знак дифференцирования, а затем, используя роторное тождество, уравнения Максвелла привести к виду:

Уравнения по виду одинаковы; их отличает размерность переменных E и Н. Кроме того, они различаются поляризацией – векторы E и Н на фронте волны лежат в ортогональных плоскостях.
Эти уравнения (их называют телеграфными) слишком сложны для геофизических приложений.

или малой проводимости среды.
Если среда  изолятор

( = 0), то из телеграфных уравнений получаются волновые уравнения

.

Сходство вида этих и других уравнений для E и Н дает основание указывать лишь одно из них – для E.
Для медленно меняющихся (низкочастотных) полей в проводящей среде ( > 0) можно пренебречь слагаемыми со вторыми производными напряженности полей по времени; получаются уравнения диффузии электромагнитного поля:

.

В непроводящей среде ( = 0) уравнения диффузии вырождаются в уравнения Лапласа.

как непосредственно, так и в анализе нестационарных полей.
Любое

переменное поле можно представить (рядом или интегралом Фурье) суммой монохроматических полей.
Рассмотрим поле с постоянной частотой :

где Ex, Ey, Ez  амплитуды; x, y, z  фазы компонент напряженности электрического поля E. (Выражение для H аналогично). Для удобства представим зависимость E(t) экспонентой, используя формулы Эйлера:

используя тот факт, что производная экспоненты равна этой экспоненте с

множителем, равным коэффициенту при переменной t:

В преобразованной на этом основании форме уравнений Максвелла используются амплитудные значение поля, на что указывают множители iω:

С помощью процедуры rot rot разделяются переменные в первых двух уравнениях Максвелла. Получаем уравнения Гельмгольца для Е (для Н аналогично):

обозначение i0 = k2 :

.

С частотой волн и проводимостью среды связана глубина проникновения

электромагнитного поля в среду – толщина скин-слоя . Это расстояние, на котором амплитуда поля уменьшается в e раз:

В проводящую среду электромагнитное поле проникает тем глубже, чем больше сопротивление среды и больше период (ниже частота) поля.
На разных частотах работают разные комплексы определяющих свойств пород, в которые входят , ,  и частота электромагнитного поля . Для гармонического поля они комплексны и в математическом смысле (содержат i).

.

а низкочастотные могут проходить в среде, близкой по свойствам к

диэлектрикам, без изменения амплитуды. Реальные горные породы, хотя имеют довольно высокие удельные сопротивления, диэлектриками не являются. Электромагнитные возмущения проникают тем глубже, чем ниже их частота.
Отсюда следуют важные выводы:
1) Для изучения глубокозалегающих объектов выгоднее использовать низкочастотное электромагнитное поле; частота должна быть тем ниже, чем больше глубина исследований и чем ниже удельное сопротивление покрывающей объекты изучения толщи пород.
2) Изменение частоты электромагнитного поля можно использовать как зондирующий фактор для изучения геоэлектрического разреза на разных глубинах.

E и H в общем случае не определяются, но можно оценить

их отношения – импедансы Z.
В однородном полупространстве

Импеданс Z – комплексное сопротивление среды при распространении электромагнитного поля; он соответствует волновому сопротивлению однородного полупространства, а в неоднородной среде он приобретает смысл кажущегося и называется входным импедансом.
Задача интерпретации электромагнитных данных – перейти от этого параметра к реальным характеристикам среды. Это достигается решением прямых задач: интегрированием уравнений Гельмгольца для заданных моделей сред при условиях сопряжения полей на границах.

фронт волны параллелен плоскости x0y; ω = const.
Выражения для

импеданса в слое с номером j:

На поверхности слоистого разреза ( j = 1) импеданс равен

В однородном полупространстве должно быть

то есть R10 = 1. Отсюда имеем определение: R1 = Z1/Z10 .
Это приведенный импеданс слоистого разреза на его поверхности. Он зависит от частоты, поэтому его также называют частотной характеристикой слоистой среды.

разрезу Z(h).
Но импеданс зависит от частоты и неудобен для интерпретации.

Для определения реальных свойств подставим в формулу для импеданса однородного полупространства волновое число:

что позволяет определить ρ, так как μ ≈ 1:

в неоднородной среде это кажущееся сопротивления, ρT.
Для слоистых разрезов строятся отношения

как функции λ / h1или зависимость ρT от

, где T – период.

током, гармоническим или импульсным, который возбуждает в среде электромагнитное поле.

Нам требуется получить нормальное поле диполя – в однородном полупространстве.
Диполь – проводник длиной rAB – меньше размеров измерительной установки (rAB < r). Момент диполя (тока в диполе) – вектор, направленный по току I, p = I rAB.
Ток гармонического диполя в однородном пространстве

Поле диполя соленоидальное и может анализироваться с помощью вектор-потенциала A

k – волновое число, ω – частота.

магнитного полей –производные вектор-потенциала A получим,
представив комплексное волновое число

k = ai +b;
b – фазовая постоянная;
a – коэффициент затухания:

exp (–ar), определяет затухание поля с расстоянием от источника r,

а другая, exp (–iωt), пространственную периодичность (волновой процесс).
Силовые линии электрического поля располагаются в меридиональных плоскостях, содержащих диполь, а магнитные силовые линии – это окружности в плоскостях, перпендикулярных оси диполя.
Поэтому имеется только одна компонента магнитного поля и только соответствующая электрическая равна нулю.
Формулы, как видим. сложны даже для однородной среды; в случае расположения источника на поверхности неоднородного полупространства они неконструктивны.
Приведены они лишь для пояснения смысла упрощений, связанных с важными в методическом отношении понятиями ближней и дальней зон.

случая, различающихся по величине |kr|, называемой параметром поля.

1) В ближней зоне |kr| << 1 (эквивалентно r << λ) измеряемые составляющие поля в пределах установки мало различаются по фазам волны в каждый момент времени. Время оказывается несущественным; диполь создает мгновенные значения поля, аналогичные полю диполя с постоянным током.
Для ближней зоны можно пренебречь малыми членами разложения в ряд экспонент в общих формулах, что дает:

Это значит, что при решении обратных задач можно использовать выводы теории стационарного поля.

от источника и низких частотах гармонического поля;
– на больших временах

становления поля, создаваемого источниками импульсного типа;
– при очень высоком удельном сопротивлении среды.
2) В дальней зоне |kr| >> 1 или r >> λ, что позволяет пренебрегать кривизной фронта электромагнитной волны, считать его плоским. Значит вместо сфероидальных волн диполя можно использовать приближение плоских волн, поля которых выражаются более простыми формулами:

обратно пропорционально квадрату расстояния до источника, тогда как Eθ и

Hφ изменяются медленнее, как 1/r, что свойственно плоским волнам.
Излучение диполя максимально в его экваториальной плоскости; пересечение ее с горизонтальной плоскостью определяет ось y, а минимум излучения – оcь x.
При таком выборе измеряются компоненты Ey и Hx, что дает импеданс

.

Задача свелась к решению для плоских волн.
Поле в промежуточной зоне, |kr| ≈ 1, из-за сложности формул обычно не изучается.
Для практических целей границы зон принимаются: ближняя зона – |kr|< 0,7; дальняя зона – |kr |> 7.

это вертикальный магнитный диполь. Вертикальное положение рамки дает горизонтальный магнитный

диполь; его можно направлять в разных азимутах.
Момент диполя M определяется: площадью рамки s, числом витков n и током I. Направление M определяет ориентировка рамки и направление циркуляции тока в ней.

Система координат и компоненты поля вертикального магнитного диполя.
M – модуль момента; θ – угол между осью диполя z и радиус-вектором точки измерения r.

витков катушки; s – площадь витка;
Для магнитного

диполя приближения ближней и дальней зон вводятся также, как и для электрического диполя.
Компоненты электрического и магнитного полей можно получить из формул для электрического диполя в ближней зоне, |kr| << 1, и в дальней зоне, |kr| >> 1. В ближней зоне мгновенные значения поля H аналогичны полю постоянного магнитного диполя, а значения E сдвинуты по фазе на π/2 относительно тока.
В дальней зоне (|kr| >> 1), как и для электрического диполя, учитываются компоненты – Ey и Hx; они дают импеданс Z.

другие обозначения стандартны.

путем мгновенного включения или переключения полярности тока в диполе нормальные

электрическое и магнитное поля вычисляются с применением преобразований Фурье.
Трансформация сигнала из временной в частотную область позволяет представить реальное изменение полей совокупностью гармонических полей. Такая возможность обеспечивается линейностью системы источник – геоэлектрический разрез. Это значит, что среда не изменяет частоту поля.
Такое представление позволяет использовать для нестационарных полей решения, полученные для монохроматического поля, а затем с помощью обратного преобразования Фурье восстанавливать закономерности распределения свойств в изучаемом разрезе.

выключении тока в диполе в момент времени t0 в среде

индуцируется электромагнитное поле.
Например, для низких частот, когда k2 = iωμ0μγ, тангенциальная составляющая электрического поля равна

Безразмерный параметр u по смыслу близок к |kr| гармонических полей; а параметр становления τ, имеющий размерность длины

подобен длине волны; время t отсчитывается от t0.

u < 1, соответствует большому времени
регистрации поля от начала

становления (t –t0) или высокому сопротивлению среды, большим значениям параметра становления τ, r << τ; поле сильнее зависит от сопротивления среды, чем в случае гармонических полей;
б) дальняя зона, u >> 1, что соответствует ранней фазе становления поля, на малых временах (t –t0), где выражения для компонент поля такие же, как для гармонических полей в волновой зоне.
В момент t0 поле изменяется скачком, а затем медленно изменяется за счет индукции в среде. Наибольшее влияние оказывает ближайшая к источнику область разреза: глубина проникновения вихревых токов (по смыслу близкая к толщине скин-слоя) составляет:

или

δ(ω) = 1,4 δ.