ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ

Содержание

1. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
2. 1.3. Электростатическое поле. Напряженность электростатического поля Почему
3. Вокруг заряда всегда есть электрическое поле, основное
4. ЭМП – есть не абстракция, а объективная
5. Силовой характеристикой поля, создаваемого зарядом q, является
6. Или в векторной формездесь r – расстояние
7. Вектор напряженности электростатического поля равен силе, действующей
8. В СИ
9. 1.4. Сложение электростатических полей. Принцип суперпозиции Если
10. Результирующая сила определится выражением:– это принцип суперпозиции или независимости действия сил
11. т.к.
12. Напряженность результирующего поля системы точечных зарядов равна
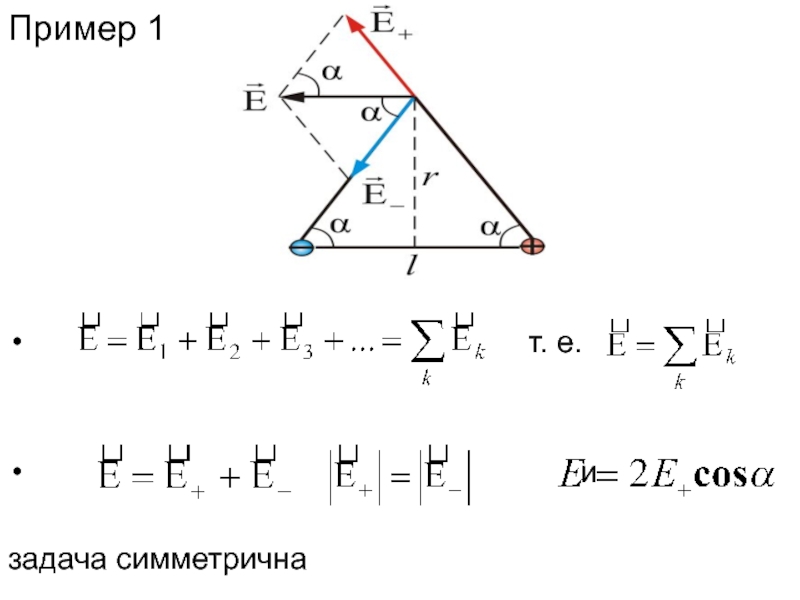
13. Пример 1
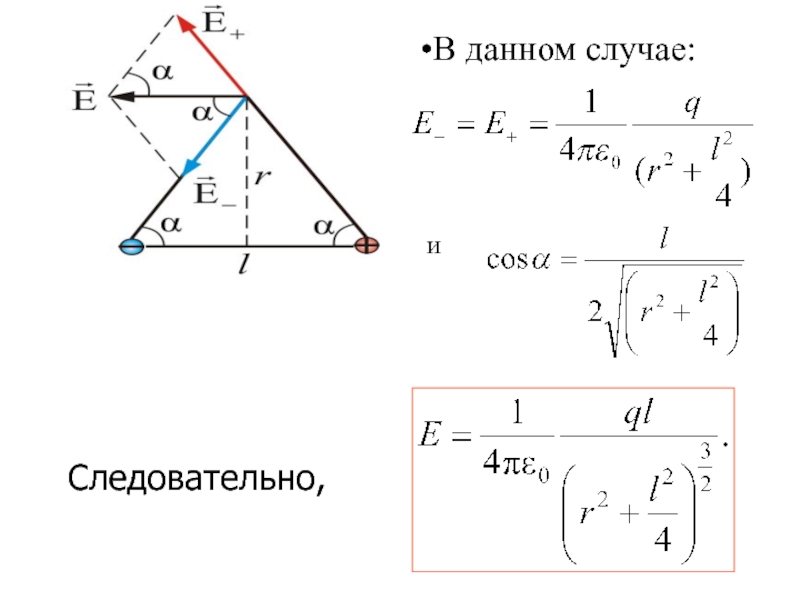
14. Следовательно,В данном случае:и
15. Рассмотрим другой пример. Найдем напряженность электростатического поля
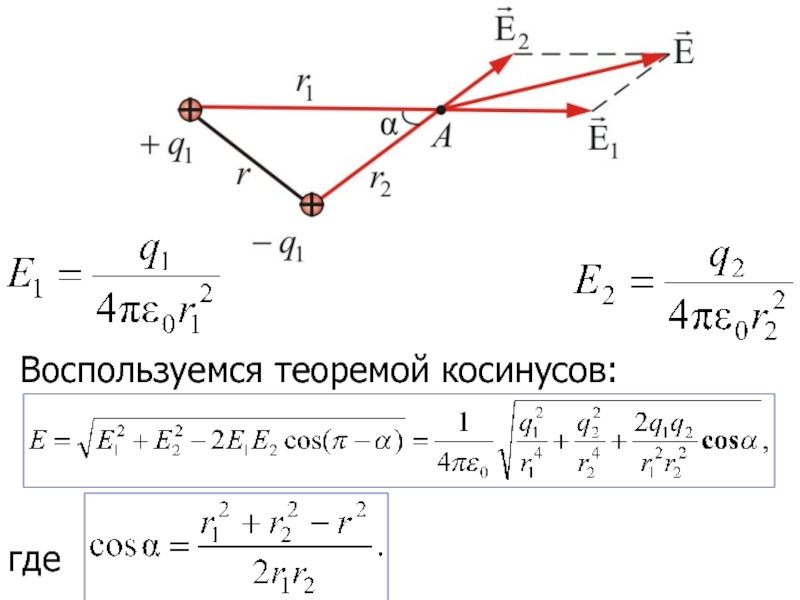
16. Воспользуемся теоремой косинусов:где
17. Если поле создается не точечными зарядами, то
18. Для решения подобных задач пользуются соответствующими значениями
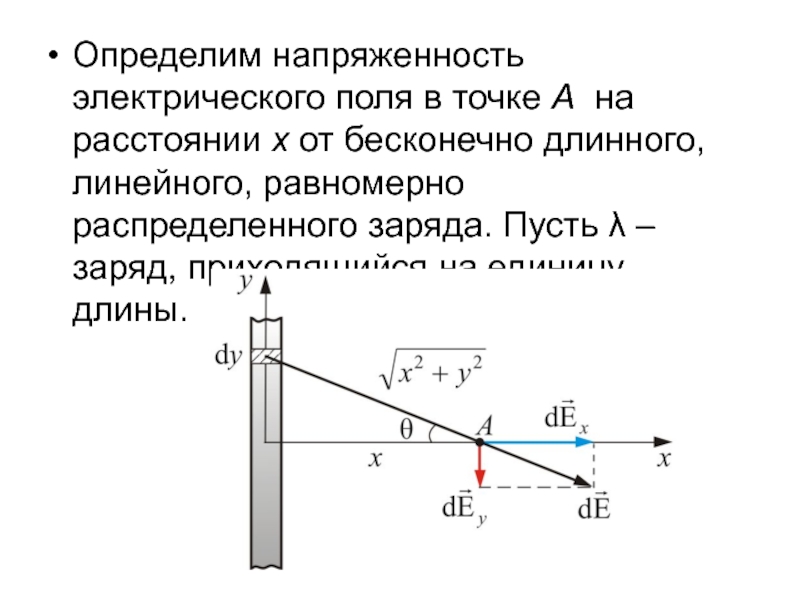
19. Определим напряженность электрического поля в точке А
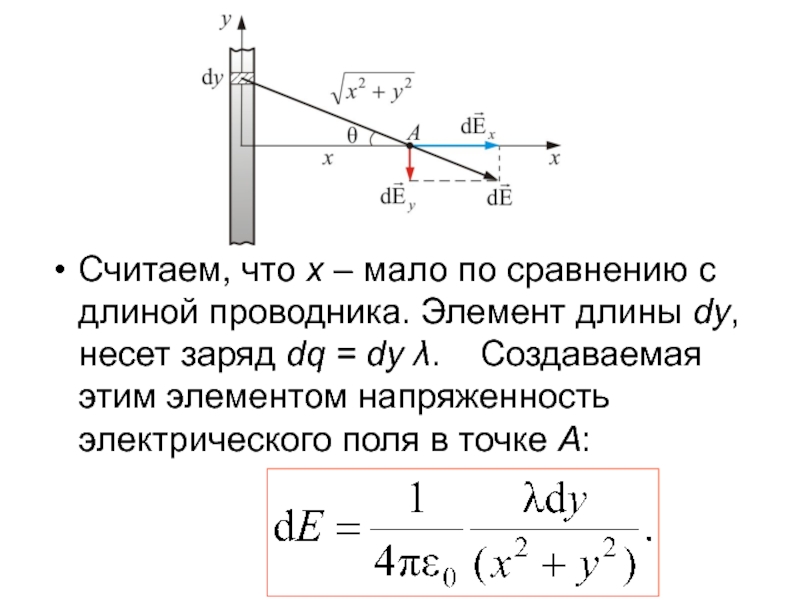
20. Считаем, что х – мало по сравнению
21. Вектор имеет проекции dEx
22. тогдаТеперь выразим y через θ. Т.к.
23. Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.
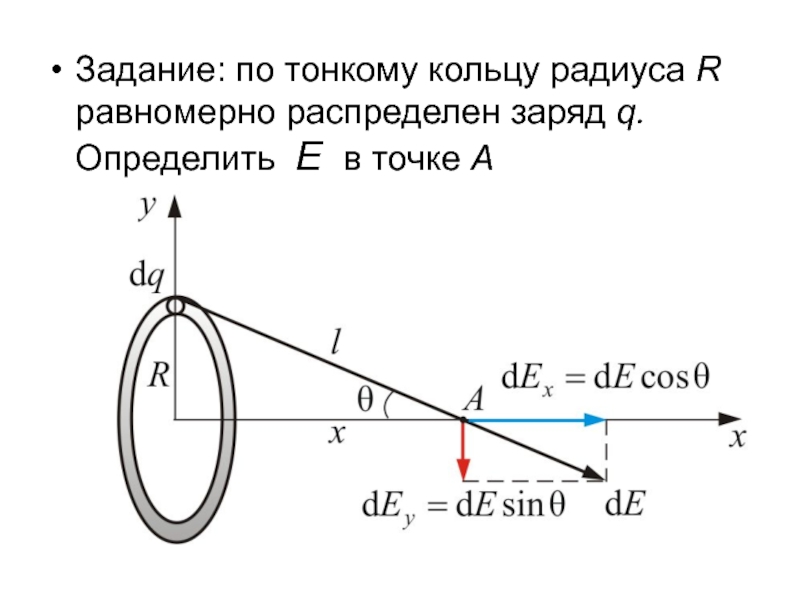
24. Задание: по тонкому кольцу радиуса R равномерно распределен заряд q. Определить Е в точке А
25. 1.5. Электростатическое поле диполя Электрическим диполем называется
26. Пример 1. Найдем Е⊥ в
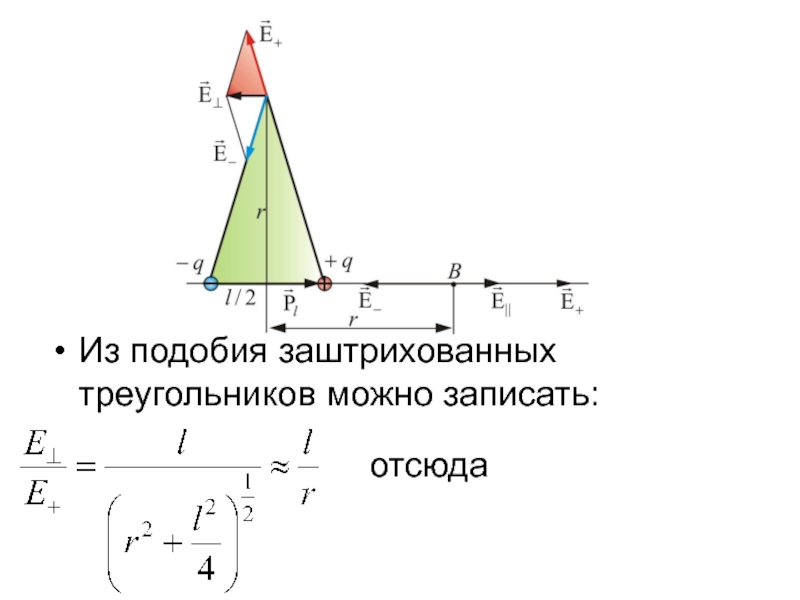
27. Из подобия заштрихованных треугольников можно записать: отсюда
28. Обозначим вектор:
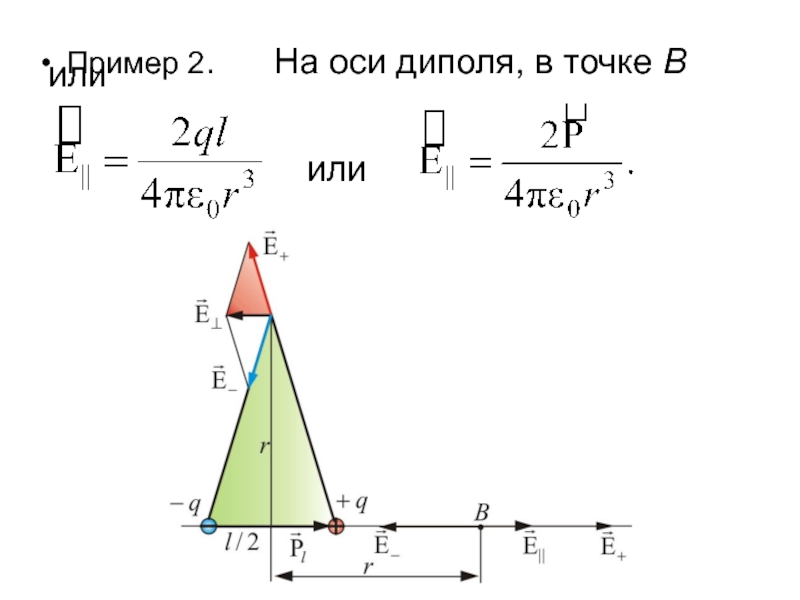
29. или Пример 2. На оси диполя, в точке В или
30. где Пример 3. В произвольной точке С где При :
31. Электрическое поле диполя.
32. Из приведенных примеров видно, что напряженность электрического
33. Слайд 33
34. Скачать презентанцию

1.3. Электростатическое поле. Напряженность электростатического поля Почему заряды взаимодействуют? Имеет место борьба двух теорий: теория дальнодействия – Ньютон, Ампер теория близкодействия – Фарадей, Максвелл и т.д. Для электростатического поля справедливы обе

Главная
Разное
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ

Слайды и текст этой презентации

Слайд 1Лекция 2. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ 2.1. Электростатическое поле. Напряженность поля 2.2.

Сложение электростатических полей. Принцип суперпозиции 2.3. Электростатическое поле диполя 2.4. Взаимодействие диполей

Лекция 2. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ 2.1. Электростатическое поле. Напряженность поля 2.2. Сложение электростатических полей. Принцип

Слайд 21.3. Электростатическое поле. Напряженность электростатического поля

Почему заряды взаимодействуют? Имеет место борьба

двух теорий:
теория дальнодействия – Ньютон, Ампер
теория близкодействия –

Фарадей, Максвелл и т.д.
Для электростатического поля справедливы обе эти теории.

1.3. Электростатическое поле. Напряженность электростатического поля Почему заряды взаимодействуют? Имеет место борьба двух теорий: теория дальнодействия –

Слайд 3Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается

в том, что на всякий другой заряд, помещенный в это

поле, действует сила.
Электрические и магнитные поля – частный случай более общего – электромагнитного поля (ЭМП).
Они могут порождать друг друга, превращаться друг в друга. Если заряды не движутся, то магнитное поле не возникает.

Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается в том, что на всякий другой заряд,

Слайд 4ЭМП – есть не абстракция, а объективная реальность – форма

существования материи, обладающая определенными физическими свойствами, которые мы можем измерить.
Не

существует статических электрических полей, не связанных с зарядами, как не существует «голых», не окруженных полем зарядов.

ЭМП – есть не абстракция, а объективная реальность – форма существования материи, обладающая определенными физическими свойствами, которые

Слайд 5Силовой характеристикой поля, создаваемого зарядом q, является отношение силы действующей

на заряд к величине этого заряда называемое напряженностью электростатического поля,

т.е.

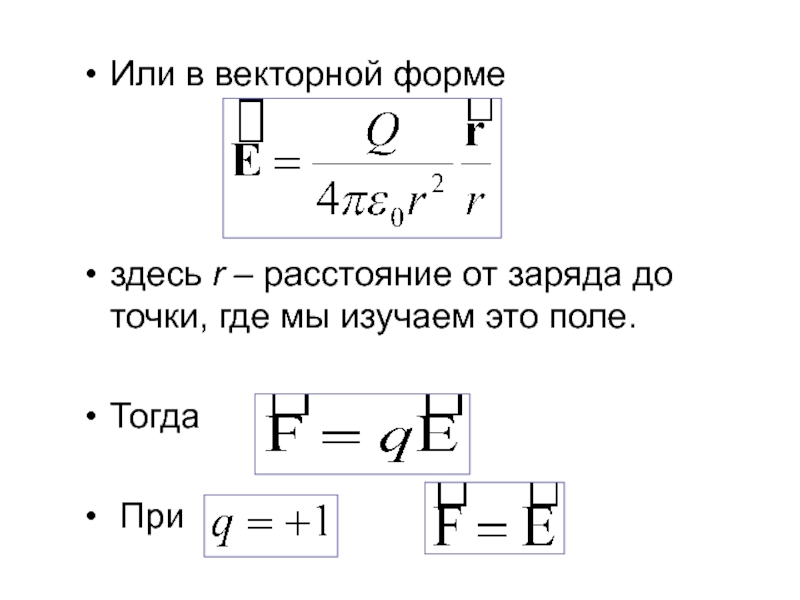
Слайд 6Или в векторной форме

здесь r – расстояние от заряда до

точки, где мы изучаем это поле.

Тогда

При

Или в векторной формездесь r – расстояние от заряда до точки, где мы изучаем это поле. Тогда

Слайд 7Вектор напряженности электростатического поля равен силе, действующей в данной точке

на помещенный в нее пробный единичный положительный заряд.
Единица измерения

напряженности электростатического поля – ньютон на кулон (Н/Кл).
1 Н/Кл – напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н.

Вектор напряженности электростатического поля равен силе, действующей в данной точке на помещенный в нее пробный единичный положительный

Слайд 8В СИ

размерность напряженности

Слайд 91.4. Сложение электростатических полей. Принцип суперпозиции

Если поле создается несколькими точечными

зарядами, то на пробный заряд q действует со стороны заряда

qk такая сила, как если бы других зарядов не было.

1.4. Сложение электростатических полей. Принцип суперпозиции Если поле создается несколькими точечными зарядами, то на пробный заряд q

Слайд 10Результирующая сила определится выражением:

– это принцип суперпозиции или независимости действия

сил

Слайд 11т.к.

то – результирующая напряженность поля в точке,

где расположен пробный заряд, так же подчиняется принципу суперпозиции:

Это соотношение выражает принцип наложения или суперпозиции электрических полей и представляет важное свойство электрического поля.

Слайд 12Напряженность результирующего поля системы точечных зарядов равна векторной сумме напряженностей

полей, созданных в данной точке каждым из них в отдельности.

Напряженность результирующего поля системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым из

Слайд 13Пример 1

т. е.

и

задача симметрична

Слайд 14

Следовательно,
В данном случае:
и

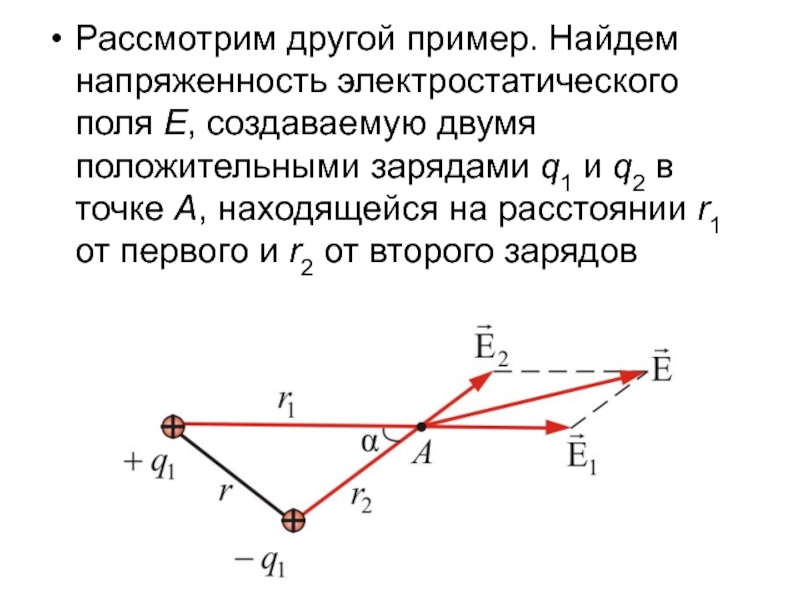
Слайд 15Рассмотрим другой пример. Найдем напряженность электростатического поля Е, создаваемую двумя

положительными зарядами q1 и q2 в точке А, находящейся на

расстоянии r1 от первого и r2 от второго зарядов

Рассмотрим другой пример. Найдем напряженность электростатического поля Е, создаваемую двумя положительными зарядами q1 и q2 в точке

Слайд 16

Воспользуемся теоремой косинусов:

где

Слайд 17Если поле создается не точечными зарядами, то используют обычный в

таких случаях прием. Тело разбивают на бесконечно малые элементы и

определяют напряженность поля создаваемого каждым элементом, затем интегрируют по всему телу:

где – напряженность поля, обусловленная заряженным элементом. Интеграл может быть в зависимости от формы тела линейным, по площади или по объему.

Если поле создается не точечными зарядами, то используют обычный в таких случаях прием. Тело разбивают на бесконечно

Слайд 18Для решения подобных задач пользуются соответствующими значениями плотности заряда:

– линейная плотность заряда, измеряется в Кл/м;

– поверхностная плотность заряда измеряется в Кл/м2;

– объемная плотность заряда, измеряется в Кл/м3.

Слайд 19Определим напряженность электрического поля в точке А на расстоянии х

от бесконечно длинного, линейного, равномерно распределенного заряда. Пусть λ –

заряд, приходящийся на единицу длины.

Определим напряженность электрического поля в точке А на расстоянии х от бесконечно длинного, линейного, равномерно распределенного заряда.

Слайд 20Считаем, что х – мало по сравнению с длиной проводника.

Элемент длины dy, несет заряд dq = dy λ.

Создаваемая этим элементом напряженность электрического поля в точке А:

Считаем, что х – мало по сравнению с длиной проводника. Элемент длины dy, несет заряд dq =

Слайд 21Вектор имеет проекции dEx и dEy причем

Т.к. проводник бесконечно длинный, а задача симметричная, то у – компонента вектора обратится в ноль (скомпенсируется), т.е. .

Слайд 22тогда

Теперь выразим y через θ. Т.к.

то
и
тогда

Слайд 23Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно

пропорционально расстоянию до заряда.

Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.

Слайд 24Задание: по тонкому кольцу радиуса R равномерно распределен заряд q.

Определить Е в точке А

Слайд 251.5. Электростатическое поле диполя

Электрическим диполем называется система двух одинаковых по

величине, но разноименных точечных зарядов, расстояние между которыми значи –тельно

меньше расстояния до тех точек, в которых определяется поле системы

Плечо диполя – вектор, направленный от отрицательного заряда к положительному и численно равный расстоянию между зарядами.

1.5. Электростатическое поле диполя Электрическим диполем называется система двух одинаковых по величине, но разноименных точечных зарядов, расстояние

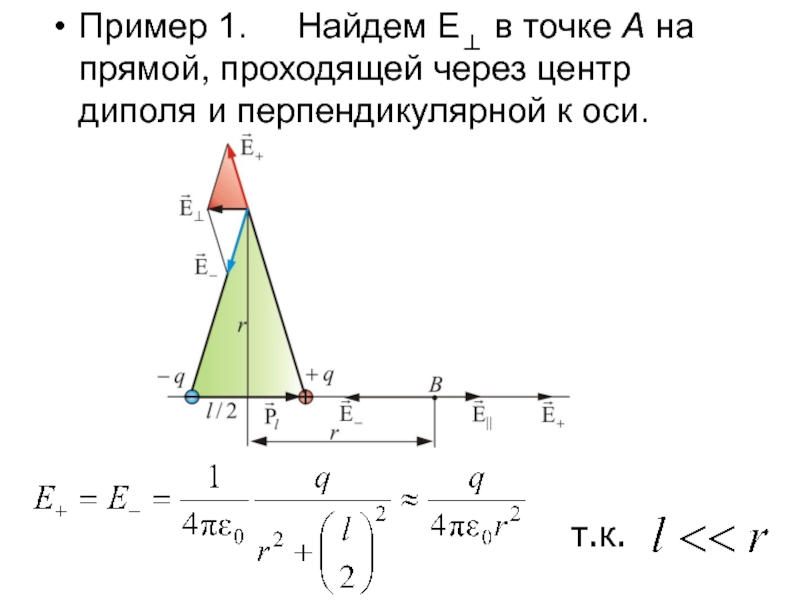
Слайд 26Пример 1. Найдем Е⊥ в точке А на

прямой, проходящей через центр диполя и перпендикулярной к оси.

т.к.

Пример 1. Найдем Е⊥ в точке А на прямой, проходящей через центр диполя и перпендикулярной

Слайд 27Из подобия заштрихованных треугольников можно записать:

отсюда

Слайд 28Обозначим вектор: –

электрический момент диполя (или дипольный момент) – произведение положительного заряда

диполя на плечо .
Направление совпадает с направлением , т.е. от отрицательного заряда к положительному.

Тогда, учитывая что получим:

или

Слайд 29или
Пример 2. На оси диполя, в точке

В

или

Слайд 30где
Пример 3. В произвольной точке С

где

При :

Слайд 31Электрическое поле диполя.

Слайд 32Из приведенных примеров видно, что напряженность электрического поля системы зарядов

равна геометрической сумме напряженностей полей каждого из зарядов в отдельности

(принцип суперпозиции).

Из приведенных примеров видно, что напряженность электрического поля системы зарядов равна геометрической сумме напряженностей полей каждого из

Слайд 33

Скачать презентацию

Разделы презентаций