до него такие же
результаты, даже с ещё большей точностью, получил Кавендиш.
Результаты работ Кавенди-ша хранились в семейном архиве и были опубликованы только спустя сто лет); найденный
последним закон электрических взаимодействий дал возможность Грину, Гауссу и Пуассону
создать изящную в математическом отношении теорию. Самую существенную часть элект-
ростатики составляет теория потенциала, созданная Грином и Гауссом. Очень много опыт-
ных исследований по электростатике было произведено Рисом, книги которого составляли
в прежнее время главное пособие при изучении этих явлений.
Шарль Огюстен Кулон
(Charles-Augustin de Coulomb) 1736-1806
Генри Кавендиш
(Henry Cavendish)
1731 - 1810
Карл Фридрих Гаусс
(Johann Carl
Friedrich Gauß)
1777-1855
Пуассон
(Siméon Denis Poisson)
1781-1840
Питер Рис
(Peter Rieß)
1805 – 1883
------------------------
Георг Грин
(George Green)
1793-1841



![ЭЛЕКТРОСТАТИКА Определение [1]Физическая энциклопедия в 5-ти томах.Изд. «Советская энциклопедия», М., 1990 г.Схема эксперимен-тальной установки Ш. Кулона Определение [1]Физическая энциклопедия в 5-ти томах.Изд. «Советская энциклопедия», М., 1990 г.Схема эксперимен-тальной установки Ш. Кулона](/img/thumbs/ac1935ff50d11b141f20b2a3ce18ab51-800x.jpg)


![ЭЛЕКТРОСТАТИКА Диполь, квадруполь и более сложные мультиполи [3]P0 = 1 P1 Диполь, квадруполь и более сложные мультиполи [3]P0 = 1 P1 = z](/img/thumbs/c4a4d088e8201bdc0b11974d34dd085a-800x.jpg)

![ЭЛЕКТРОСТАТИКА Определение [1]Силовыми линиями неудобно пользоваться, если заряд рас-пределён в пространстве, т.к. Определение [1]Силовыми линиями неудобно пользоваться, если заряд рас-пределён в пространстве, т.к. в этом случае плотность си-ловых линий](/img/thumbs/15868f753819154a344acd10ffcb1928-800x.jpg)

![ЭЛЕКТРОСТАТИКА Дифференциальные уравнения электростатики [3]Поток вектора через бесконечно малый кубdiv Adiv E Дифференциальные уравнения электростатики [3]Поток вектора через бесконечно малый кубdiv Adiv E = ρ/εo](/img/thumbs/497ad71d52884b9880ab1ea158ecbc18-800x.jpg)
![ЭЛЕКТРОСТАТИКА Дискретность электрического заряда [7]Задача ТомсонаСхема эксперимента МилликенаРоберт Ми́лликен Robert Andrews Millikan 1868 -1953 Дискретность электрического заряда [7]Задача ТомсонаСхема эксперимента МилликенаРоберт Ми́лликен Robert Andrews Millikan 1868 -1953 - американский физик В 1923 получил Нобелевскую](/img/thumbs/75edadfa10348a5a6ad57c0612796a07-800x.jpg)
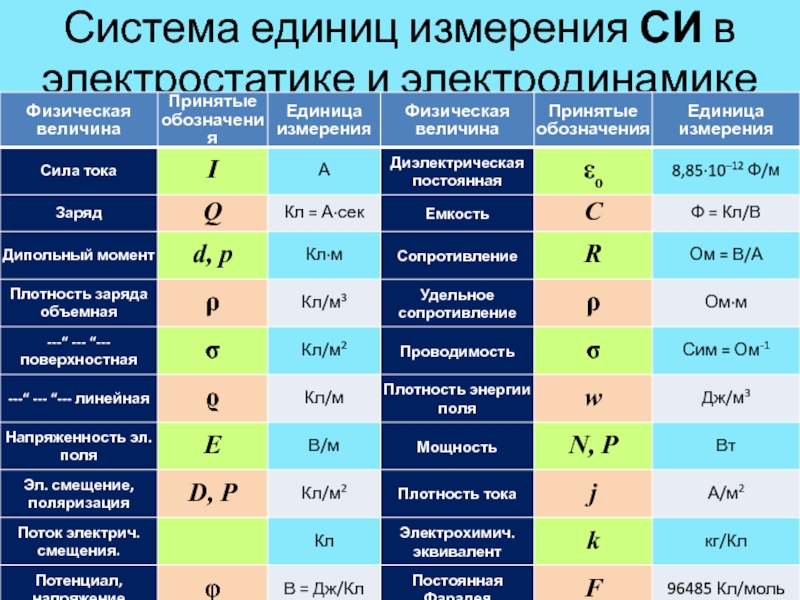
![ЭЛЕКТРОСТАТИКА Определение [1]В этой статье, взятой из физической энциклопедии, фигурирует абсолют-ная диэлектрическая Определение [1]В этой статье, взятой из физической энциклопедии, фигурирует абсолют-ная диэлектрическая проницаемость ε, которую мы обычно заменяем](/img/thumbs/274883925c7ef5eafc5837735361e9d1-800x.jpg)
![ЭЛЕКТРОСТАТИКА Плотность энергии поля [5]Задачи на нахождение ёмкости конденсатора123456Работа по раздвижению обкладок Плотность энергии поля [5]Задачи на нахождение ёмкости конденсатора123456Работа по раздвижению обкладок конденсатораПоле одной пластиныСила между пластинами](/img/thumbs/6236524053bdacdec4ff8e66249c5c45-800x.jpg)

![ЭЛЕКТРОСТАТИКА Электростатика проводников [4]Если внутри проводника есть эле-ктрическое поле, то в нём Электростатика проводников [4]Если внутри проводника есть эле-ктрическое поле, то в нём идёт ток. Если проводник изолирован, то](/img/thumbs/c4315d5fd02baa4ec99580fed28f3282-800x.jpg)
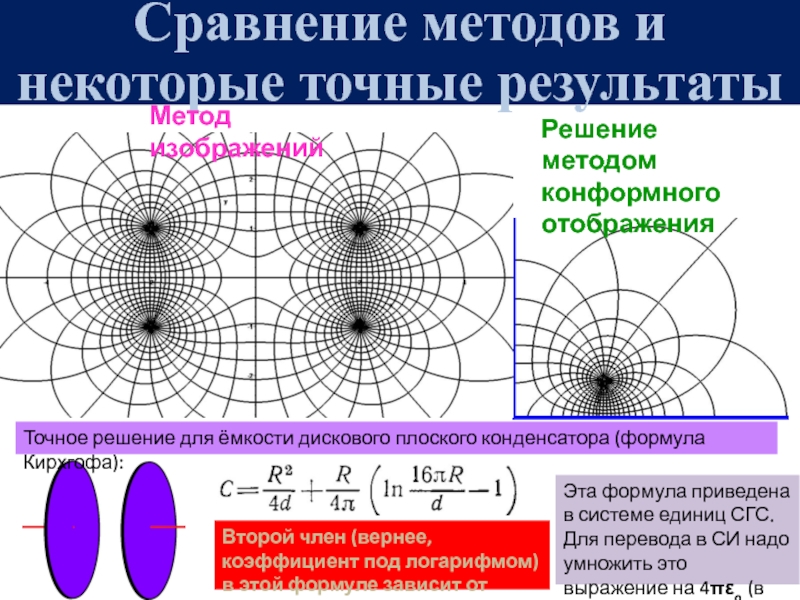
![ЭЛЕКТРОСТАТИКА Метод изображений [2]Снизу, под плоскостью, поля нет. Следовательно, энергия взаимодействия с Метод изображений [2]Снизу, под плоскостью, поля нет. Следовательно, энергия взаимодействия с проводни-ком, в 2 раза меньше, чем](/img/thumbs/7716f47eb86b402f2c0583ffeddd2a02-800x.jpg)
![ЭЛЕКТРОСТАТИКА Эллипсоидальные координатыЭквипотенци-альные линии проводящего эллипсоида во внешнем поле[2] Эллипсоидальные координатыЭквипотенци-альные линии проводящего эллипсоида во внешнем поле[2]](/img/thumbs/7cafa9a137201b870f5feedd15f4d341-800x.jpg)
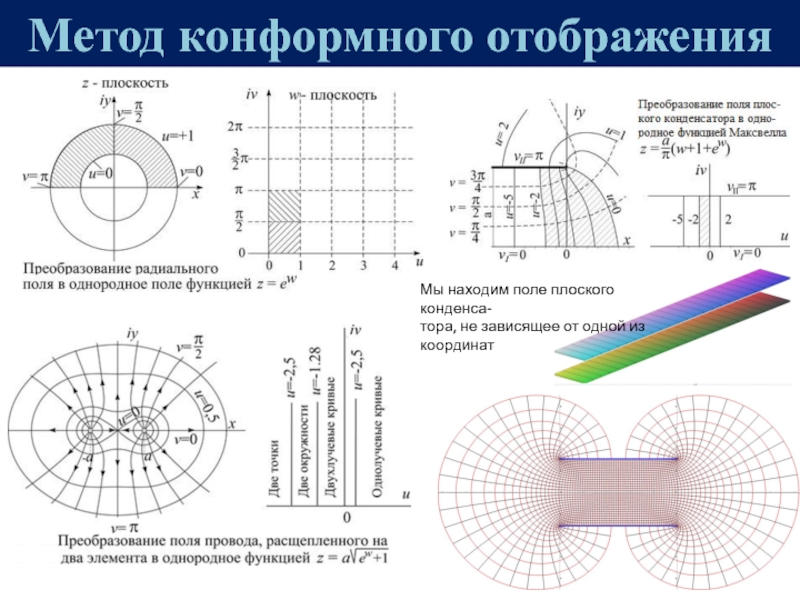
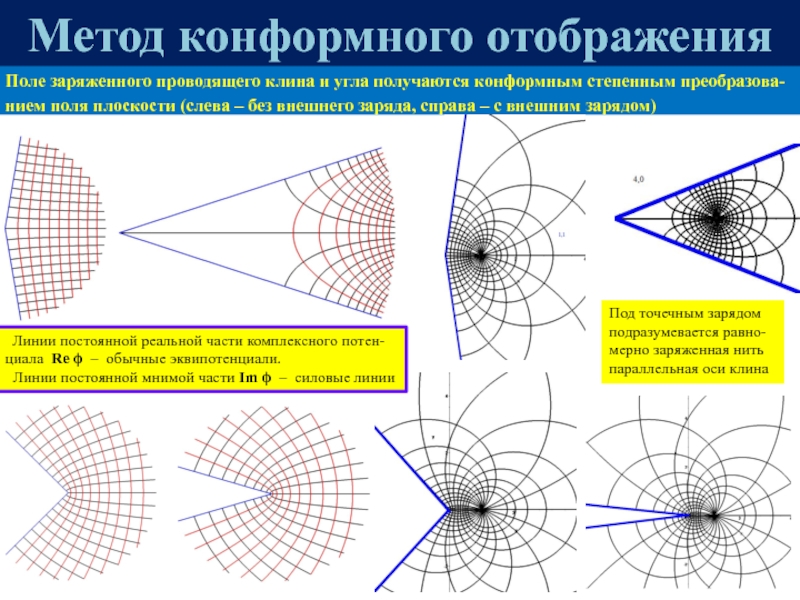
![ЭЛЕКТРОСТАТИКА Метод конформного отображения [3]Конформные отображения изменяют объём, но сохраняют все углы Метод конформного отображения [3]Конформные отображения изменяют объём, но сохраняют все углы и формы в малых масштабахЗдесь приве-дён](/img/thumbs/e470805083fc5268624f81d4f325e2fb-800x.jpg)


![ЭЛЕКТРОСТАТИКА Численные методы электростатики[8]Метод конечных элементов для численного расчёта электростатического поляОдин из Численные методы электростатики[8]Метод конечных элементов для численного расчёта электростатического поляОдин из возможных контуров конечных элементов для цилиндра.Поля](/img/thumbs/8422fcdf5ba502fbc9348b531d594236-800x.jpg)
![ЭЛЕКТРОСТАТИКА Разные электрические поляМолекулярные поля[13]Электрическое поле человека[12]На рисунке показан примерный ход эквипотенциалей Разные электрические поляМолекулярные поля[13]Электрическое поле человека[12]На рисунке показан примерный ход эквипотенциалей в определённый момент возбуждения сердца. Цифры](/img/thumbs/edba00d8806b359099d53c7a72b7f4b6-800x.jpg)


![ЭЛЕКТРОСТАТИКА Приложение [5] Приложение [5]](/img/thumbs/1f2a6327b6da13404afb570e1f48ded7-800x.jpg)