Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы математической статистики
Содержание
- 1. Элементы математической статистики
- 2. «статистика»происходит от латинского слова status - состояние,
- 3. Математическая статистика возникла и развивалась параллельно с
- 4. В XX в. наиболее существенный вклад в
- 5. Математическая статистика – раздел математики, посвященный математическим методам
- 6. Математическая статистика исходит из предположения, что наблюдаемая
- 7. Проверка различных научных гипотез и моделей является
- 8. Закон больших чисел – это объективный математический
- 9. Статистический подход – выявление закономерной изменчивости на фоне
- 10. Аппарат математической статистики является инструментом для отсеивания закономерностей
- 11. В теории вероятностей рассматриваются случайные величины с заданным
- 12. Характеристика областей применения аппарата Теория вероятностей Модель,
- 13. Предмет исследования в математической статистике - совокупность
- 14. Допустим, повторением одного и того же случайного
- 15. Если сделать предположения о распределении или о
- 16. Пусть каждому i объекту соответствует значение xi,
- 17. Пусть количество реально наблюдаемых объектов из N
- 18. Выборка из генеральной совокупности должна обладать следующими
- 19. Формы представления выборки из генеральной совокупности Представление
- 20. Пример:измерена масса тела 10 девочек 6 лет.
- 21. Отдельные значения статистического ряда называются вариантами. Если
- 22. 2. Представление выборки в виде вариационного ряда
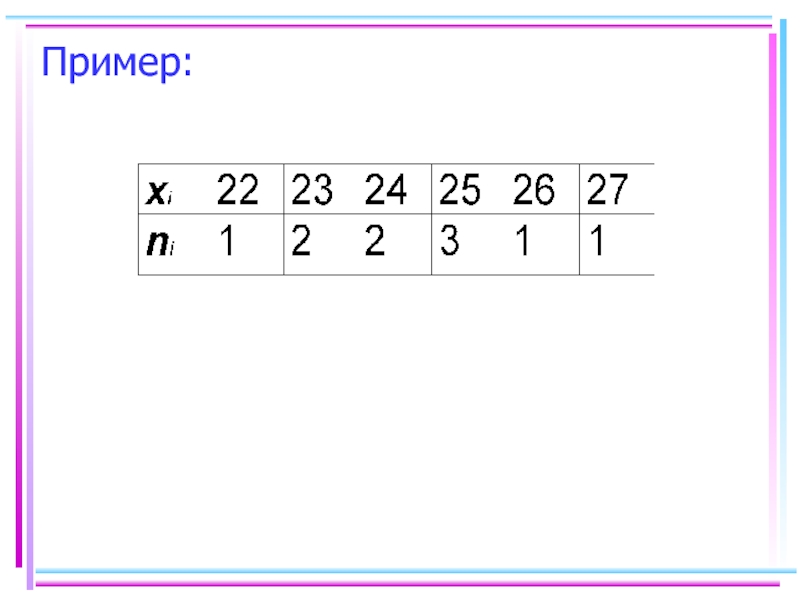
- 23. Пример:Вариационный ряд: 22 23 23 24 24 25 25 25 26 27
- 24. Таблица, в первой строке которой записаны все
- 25. Пример:
- 26. Понятие репрезентативная выборка не всегда можно связать
- 27. Форма представления выборки из генеральной совокупности в
- 28. Необходимо помнить! Члены вариационного ряда, в отличие
- 29. Представление выборки в группированном виде. Такая форма представления
- 30. Для определения числа L интервалов искусственного группирования пользуются формулой Старджеса
- 31. Иногда L может быть задано природой исследуемого
- 32. Последовательность процедуры группирования неупорядоченной выборки из генеральной
- 33. Определение ширины интервалов гистограммы (при равноточном группировании)
- 34. Для того чтобы x(1) и х(n) попали
- 35. При этом последовательность границ интервалов разбиения будет
- 36. Пример Даны объемы ежедневной выработки в течение месяц
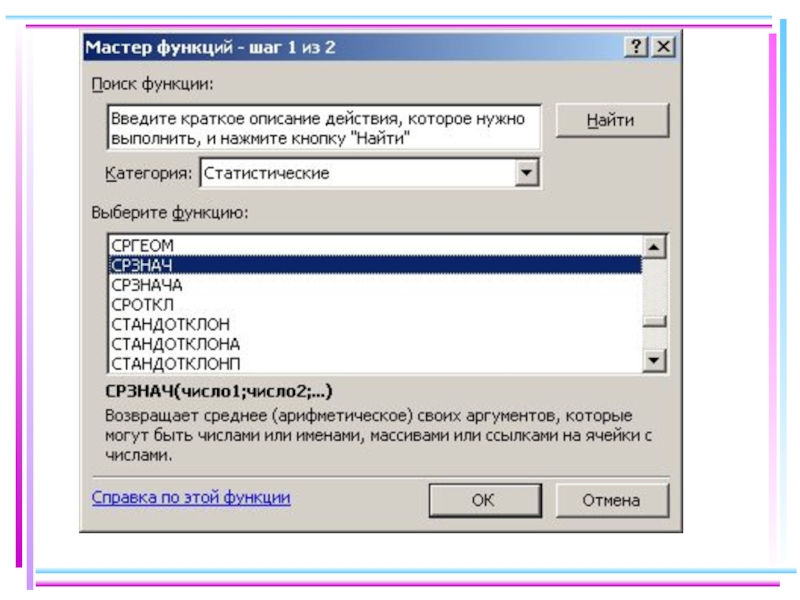
- 37. В EXCEL Находим основные числовые характеристики выборки: выборочную
- 38. Слайд 38
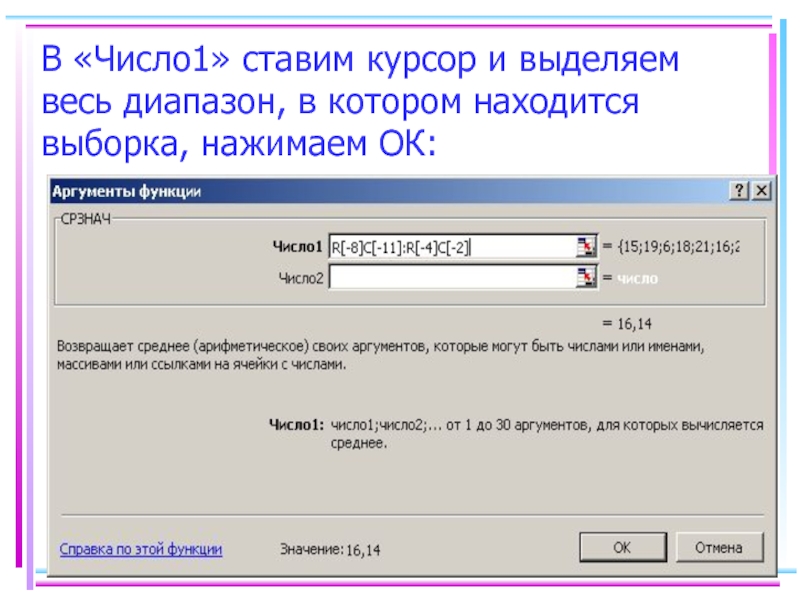
- 39. В «Число1» ставим курсор и выделяем весь диапазон, в котором находится выборка, нажимаем ОК:
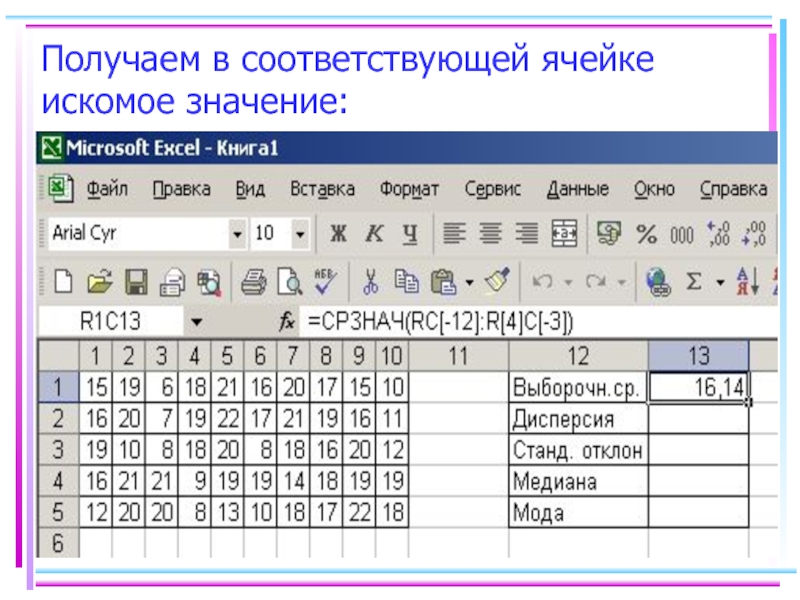
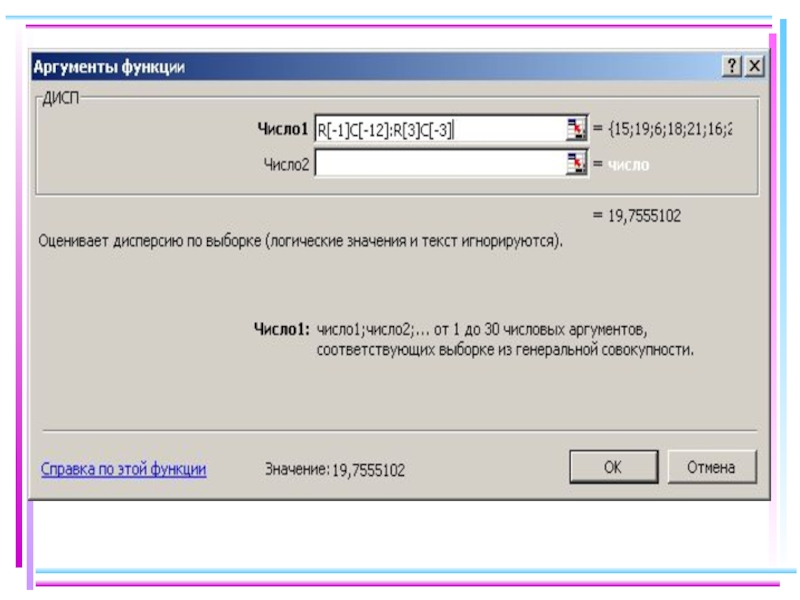
- 40. Получаем в соответствующей ячейке искомое значение:
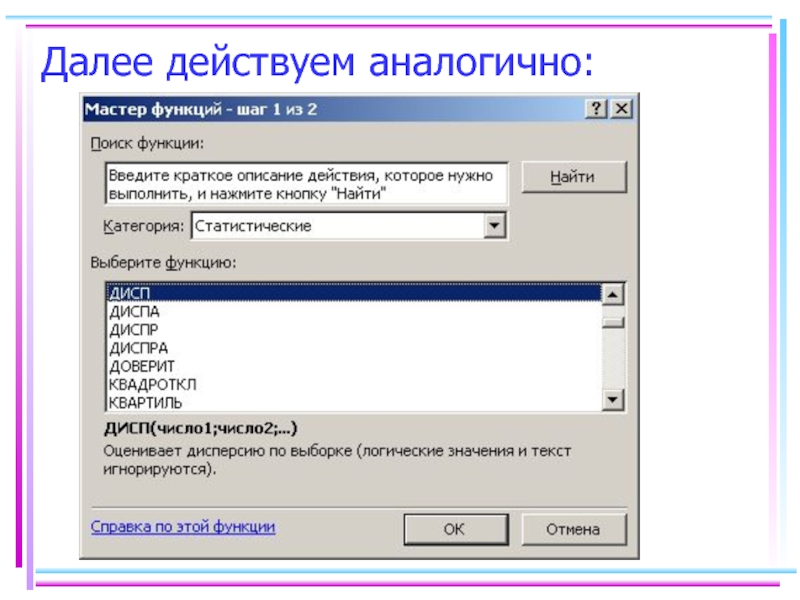
- 41. Далее действуем аналогично:
- 42. Слайд 42
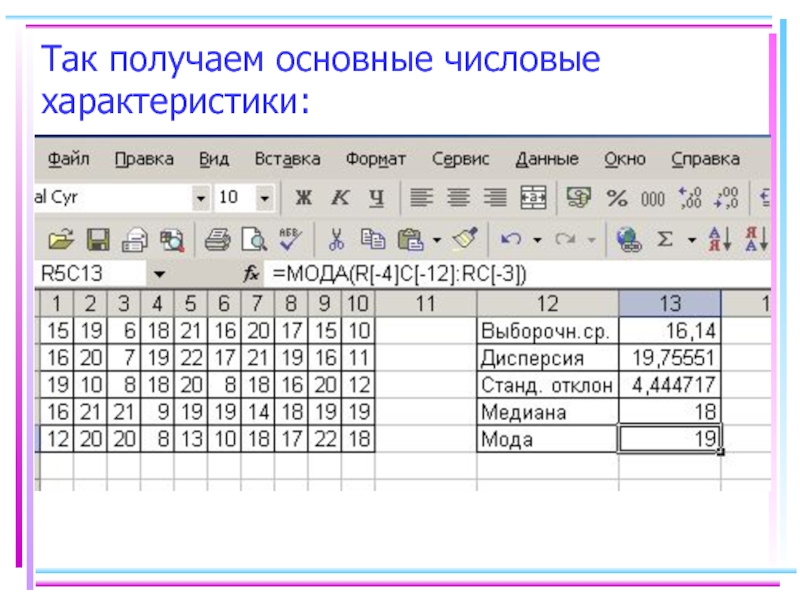
- 43. Так получаем основные числовые характеристики:
- 44. Представим выборку в группированном виде. 1. Формируем вариационный
- 45. 3. Определяем число интервалов разбиения по формуле
- 46. Строим вариационный ряд границ интервалов группирования (без
- 47. 6. Находим количество элементов выборки nj, попавших
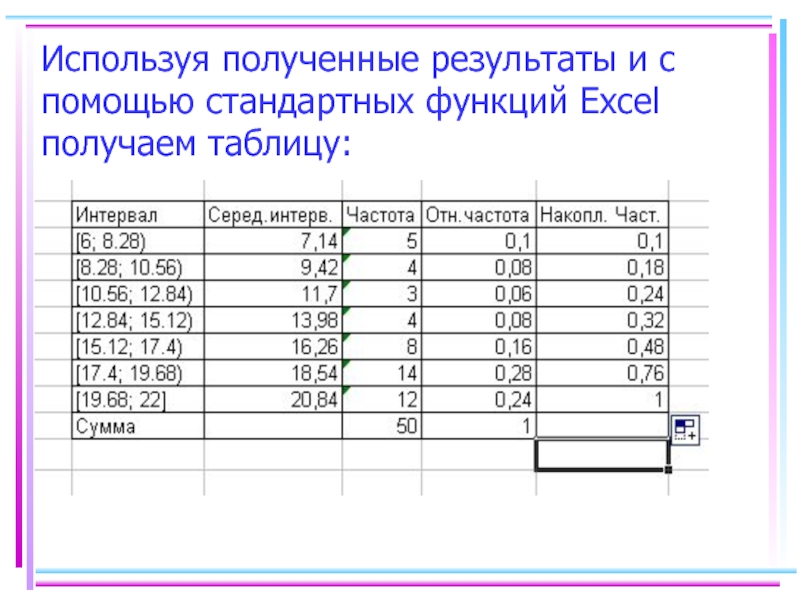
- 48. Используя полученные результаты и с помощью стандартных функций Excel получаем таблицу:
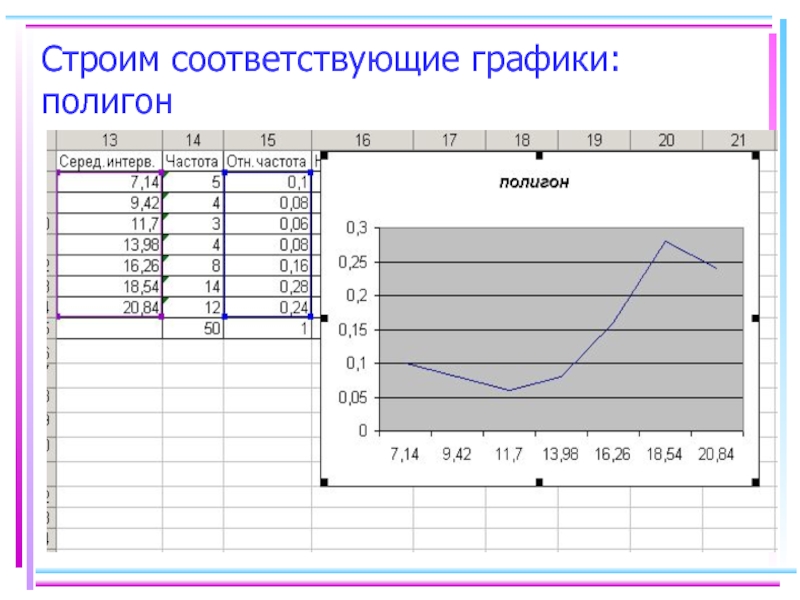
- 49. Строим соответствующие графики: полигон
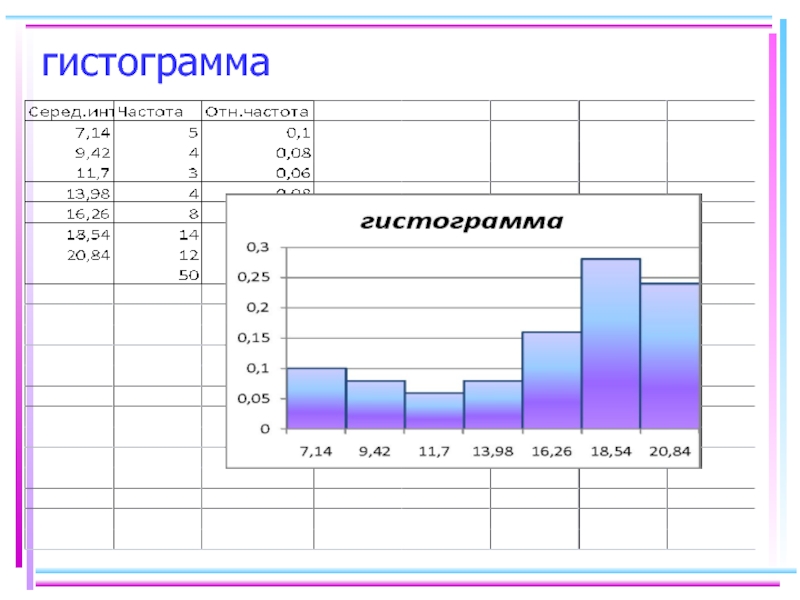
- 50. гистограмма
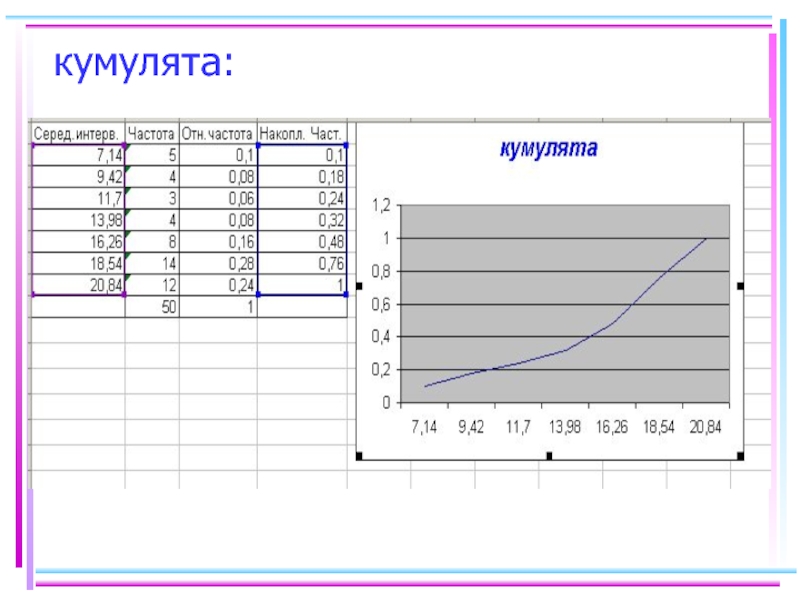
- 51. кумулята:
- 52. Это важно! От негруппированной выборки всегда можно перейти
- 53. Характеристики случайной величины, полученные по выборке из
- 54. Все методы математической статистики можно разделить на
- 55. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2«статистика»
происходит от латинского слова status - состояние, положение вещей. Первоначально
оно употреблялось в значении «политическое состояние».
слово вошло в XVIII в. и первоначально употреблялось в значении «государствоведение».Слайд 3Математическая статистика возникла и развивалась параллельно с теорией вероятностей (XVII
в.)
Дальнейшее развитие математической статистики (вторая половина XIX — начало XX
в.) обязано П. Л. Чебышеву,
А. А. Маркову,
А. М. Ляпунову,
К. Гауссу,
А. Кетле,
Ф. Гальтону,
К.Пирсону и др.
Слайд 4 В XX в. наиболее существенный вклад в математическую статистику был
сделан
советскими :
В. И. Романовский, Е. Е. Слуцкий,
А.Н. Колмогоров,
Н. В. Смирнов;английскими:
Стьюдент, Р. Фишер, Э. Пирсон;
американскими математиками:
Ю. Нейман, А. Вальд.
Слайд 5Математическая статистика
– раздел математики, посвященный математическим методам систематизации, обработки и
использования статистических данных для научных и практических выводов. Такое определение
сформулировано математиками А.Н. Колмогоровым и Ю.В. Прохоровым.Слайд 6 Математическая статистика исходит из предположения, что наблюдаемая изменчивость окружающего мира
имеет два источника:
действие известных причин и факторов. Они порождают изменчивость,
закономерно объяснимую.действие случайных причин и факторов.
Большинство природных и общественных явлений обнаруживают изменчивость, которая не может быть целиком объяснена закономерными причинами.
В таком случае прибегают к концепции случайной изменчивости.
Выражение «случайный» в данном контексте означает «подчиняющийся законам теории вероятностей».
Слайд 7 Проверка различных научных гипотез и моделей является случайным событием, так
как результаты исследования определяются большим количеством заранее непредсказуемых факторов.
Определенные
закономерности можно выявить только в случае массовых наблюдений вследствие закона больших чисел. Слайд 8Закон больших чисел –
это объективный математический закон, согласно которому
совместное действие большого числа случайных факторов приводит к результату, почти
не зависящему от случая.Слайд 9Статистический подход
– выявление закономерной изменчивости на фоне случайных факторов и
причин.
Методы математической статистики позволяют оценить параметры имеющихся закономерностей, проверить
те или иные гипотезы об этих закономерностях.Слайд 10Аппарат математической статистики
является инструментом для отсеивания закономерностей от случайностей.
Задача
исследователя
- накапливать информацию об окружающем мире, пытаясь выделить закономерности
из случайностей.Слайд 11В теории вероятностей
рассматриваются случайные величины с заданным распределением или случайные
эксперименты, свойства которых целиком известны. Предмет теории вероятностей – свойства
и взаимосвязи этих величин (распределений).Математическая статистика
опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.
Слайд 12Характеристика областей применения аппарата
Теория вероятностей
Модель, описывающая изучаемое явление
или объект, известна априори (до опыта). Есть сведения обо всей
генеральной совокупности, описывающей исследуемое явление.Используемый математический аппарат не зависит от предметной области.
Выводы о поведении исследуемого объекта или явления делаются по всей генеральной совокупности.
Математическая статистика
Модель, описывающая исследуемое явление, априори неизвестна.
Для определения модели можно проводить пробные испытания (сформировать выборку из генеральной совокупности).
Иногда модель может быть задана априори с точностью до неизвестных параметров.
Значения неизвестных параметров модели могут быть приближенно получены по выборке из генеральной совокупности.
Выводы о поведении объекта или явления делаются по выборке ограниченного объема и распространяются на всю генеральную совокупность.
Слайд 13Предмет исследования в математической статистике
- совокупность объектов, однородных относительно
некоторых признаков.
Например:
дети 10 лет г. Братска;
пловцы-мастера спорта России.
Слайд 14 Допустим, повторением одного и того же случайного эксперимента в одинаковых
условиях получен набор числовых результатов.
При этом у исследователя возникают
вопросы: Если мы наблюдаем одну случайную величину – как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?
Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин — что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?
Слайд 15 Если сделать предположения о распределении или о его свойствах до
эксперимента, то по опытным данным обычно требуется подтвердить или опровергнуть
эти гипотезы с определенной степенью достоверности.Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента:
о наличии функциональной зависимости между наблюдаемыми величинами,
о нормальности распределения, о его симметричности,
о наличии у распределения плотности
или о его дискретном характере, и т.д.
Слайд 16 Пусть каждому i объекту соответствует значение xi, , где N
- количество всех исследуемых объектов.
Совокупность всех возможных значений (теоретически
домысливаемых) N объектов называется генеральной совокупностью, а N – объемом генеральной совокупности. Генеральная совокупность может быть конечной или бесконечной.
Например, изучение физической подготовленности детей 10 лет г. Иркутска.
Слайд 17Пусть количество реально наблюдаемых объектов из N равно n. Тогда
xi – выборка из генеральной совокупности,
n – объем выборки.
Слайд 18Выборка из генеральной совокупности должна обладать следующими свойствами:
каждый элемент
xi выбран случайно;
все xi имеют одинаковую вероятность попасть
в выборку; n должно быть настолько велико, насколько это позволяет решать задачу с требуемым качеством (выборка должна быть репрезентативной, представительной).
Слайд 19Формы представления выборки из генеральной совокупности
Представление выборки из генеральной
совокупности в негруппированном виде. Этот ряд называется простым статистическим рядом.
Такая форма связана с наличием сведений о каждом элементе выборки.
Слайд 20Пример:
измерена масса тела 10 девочек 6 лет. Полученные данные образуют
простой статистический ряд:
24 22 23 26 24 23 25 27
25 25Слайд 21 Отдельные значения статистического ряда называются вариантами. Если варианта хi появилась
m раз, то число m называют частотой, а ее отношение
к объему выборки m/n – относительной частотой (частостью).Слайд 22 2. Представление выборки в виде вариационного ряда
(в упорядоченном виде):
х(1) ≤ х(2) ≤ … ≤ х(i) ≤ ... ≤
х(n) .В этом случае х(i) – член вариационного ряда, или варианта. Часто х(i) называют порядковой статистикой.
Слайд 24Таблица, в первой строке которой записаны все значения величины (варианты),
во второй –- соответствующие им частоты, называется также вариационным рядом
по значениям.Слайд 26 Понятие репрезентативная выборка не всегда можно связать с её объемом
n.
Чаще это зависит от реально исследуемого объекта или явления,
объема генеральной совокупности, трудоёмкости и стоимости получения наблюдений или измерений для формирования выборки. Слайд 27 Форма представления выборки из генеральной совокупности в виде вариационного ряда
не приводит к потере информации о каждом элементе выборки, но
искажает информацию, устанавливая зависимость между соседними элементами выборки.Слайд 28 Необходимо помнить! Члены вариационного ряда, в отличие от элементов исходной
выборки, уже не являются взаимно независимыми (по причине их предварительной
упорядоченности).Слайд 29Представление выборки в группированном виде.
Такая форма представления выборки из генеральной
совокупности связана с разбиением области задания случайной величины Х на
L интервалов группирования. При этом известно только количество элементов выборки nj, , попавших в j интервал и последовательность границ интервалов разбиения.Слайд 30 Для определения числа L интервалов искусственного группирования пользуются формулой Старджеса
Слайд 31 Иногда L может быть задано природой исследуемого явления или условиями
проведения эксперимента. В этом случае ширина каждого интервала может быть
отличной от других (неравноточное группирование).На некоторых этапах статистического анализа необходимо исходную выборку представлять в группированном виде.
Слайд 32Последовательность процедуры группирования неупорядоченной выборки из генеральной совокупности
Формирование вариационного
ряда.
Выделение минимального и максимального элементов выборки
хmin = х(1),
хmax
= х(n).Определение числа интервалов группирования осуществляется из соображения точности и устанавливается эмпирическим путем в зависимости от объема выборки, либо по формуле Старджеса, либо определяется природой явления или условиями проведения эксперимента. Округление при нахождении L осуществляется до ближайшего целого числа.
Слайд 33Определение ширины интервалов гистограммы (при равноточном группировании)
Если при вычислении
h необходимо округлить результат, следует помнить, что последний интервал группирования
будет меньше ширины h при округлении в большую сторону и больше h - при округлении в меньшую сторону.Формирование последовательности границ интервалов разбиения. Образуемый вариационный ряд границ интервалов группирования будет выглядеть как
х(1), х(1) + h, х(1) + 2h, … , х(1) + (L-1) ×h, х(n).
Слайд 34Для того чтобы x(1) и х(n) попали внутрь соответственно 1-го
и L-го интервалов группирования, границы х(1) и х(n) корректируют следующим
образом:x'(1) = x(1) - h/2,
x'(n) = x(n) + h/2.
Следовательно, число интервалов разбиения увеличивается на 1
L′ = L + 1.
Слайд 35При этом последовательность границ интервалов разбиения будет представлена в виде
x’(1), х’(1) + h, х’(1) + 2h, … ,
х’(1)
+ L×h, х’(n) Определение количества элементов выборки nj, попавших в каждый j интервал.
Слайд 36Пример
Даны объемы ежедневной выработки в течение месяц (в тыс. руб.)
пятидесяти продавцов молочных изделий, работающих в разных районах города
15
19 6 18 21 16 20 17 15 1016 20 7 19 22 17 21 19 16 11
19 10 8 18 20 8 18 16 20 12
16 21 21 9 19 19 14 18 19 19
12 20 20 8 13 10 18 17 22 18.
Слайд 37В EXCEL
Находим основные числовые характеристики выборки: выборочную среднюю, выборочную дисперсию,
стандартное отклонение, моду, медиану. Для этого в Excel в отдельные
ячейки вводим данные выборки, устанавливаем курсор в желаемой ячейке, выбираем «мастер функций» «статистические», «СРЗНАЧ», нажимаем ОК:Слайд 39В «Число1» ставим курсор и выделяем весь диапазон, в котором
находится выборка, нажимаем ОК:
Слайд 44Представим выборку в группированном виде.
1. Формируем вариационный ряд
6 9
12 15 16 18 19 19 20 21
7 10 12
16 17 18 19 19 20 218 10 13 16 17 18 19 19 20 21
8 10 14 16 17 18 19 20 20 21
8 11 15 16 18 18 19 20 21 22.
Находим х(1) = 6, х(n) = 22.
Слайд 45
3. Определяем число интервалов разбиения по формуле Старджеса
L = 1
+ 3,322 lg50 = 6.6 , L = 7.
4. Находим
ширину интервала разбиения hh = (22 - 6) / 7 = 2.2857.
Ограничимся двумя знаками после запятой и получим h = 2.28. Так как h округлено в сторону уменьшения, последний интервал будет шире предыдущих.
Слайд 46Строим вариационный ряд границ интервалов группирования (без корректировки границ первого
и последнего интервалов):
[6; 8.28), [8.28; 10.56), [10.56; 12.84), [12.84; 15.12),
[15.12; 17.4), [17.4; 19.68), [19.68; 22].Слайд 476. Находим количество элементов выборки nj, попавших в j интервал:
Группированная
форма представления случайной величины не содержит информации о каждом элементе
выборки.При этом часто в качестве значения случайной величины на интервале принимается его середина.