неприменимы, например, для непрерывных случайных величин.
Действительно, пусть возможные значения случайной
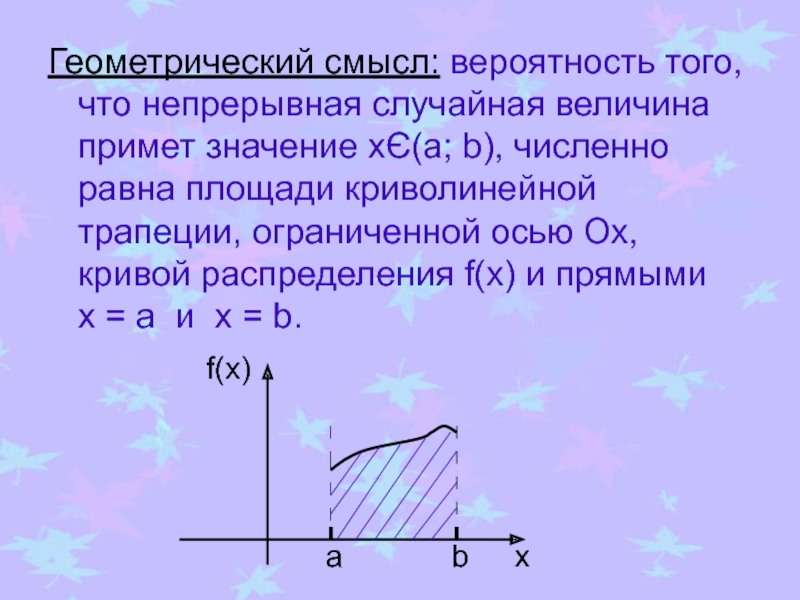
величины X полностью заполняют интервал (a;b). Можно ли составить перечень всех возможных значений X? Нет.Необходим общий способ задания любых типов случайных величин. С этой целью и вводят функции распределения вероятностей случайной величины.



![Функция распределения вероятностей случайной величины Свойства функции распределения1. Значения функции распределения принадлежат отрезку [0;1]:0 ≤ F(x) Свойства функции распределения1. Значения функции распределения принадлежат отрезку [0;1]:0 ≤ F(x) ≤ 1.2. F(x) – неубывающая ф-ция,](/img/thumbs/07cba1955caec0a9ae7566f2ffe8f5c9-800x.jpg)









![Функция распределения вероятностей случайной величины График функции распределения] График расположен в полосе, ограниченной прямыми у=0, y=1 График функции распределения] График расположен в полосе, ограниченной прямыми у=0, y=1 (1 свойство).] При возрастании х](/img/thumbs/b26d8d21055de9ce940adad28ae4a237-800x.jpg)
![Функция распределения вероятностей случайной величины ] При х ≤ а ординаты графика равны 0; при х ] При х ≤ а ординаты графика равны 0; при х ≥ b ординаты графика равны 1.0F(x)11bxa](/img/thumbs/f0ccdcb61b5da2775a50c2f9da3e4998-800x.jpg)