Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция, ее свойства и график
Содержание
- 1. Функция, ее свойства и график
- 2. ПеременныеРене́ Дека́рт 1596 — 1650, — французский
- 3. Простейшие зависимости1. Пропорциональная зависимость: у=кх, к- постоянное
- 4. Определение функцииФункция – это такая зависимость переменной
- 5. Способы задания функции:Аналитический(формулами) например:Табличный (на практике часто
- 6. График функцииГрафиком функции y = f(x) называется
- 7. Область определения функцииСовокупность всех значений аргумента х,
- 8. Область значений (множество значений) функции Совокупность всех
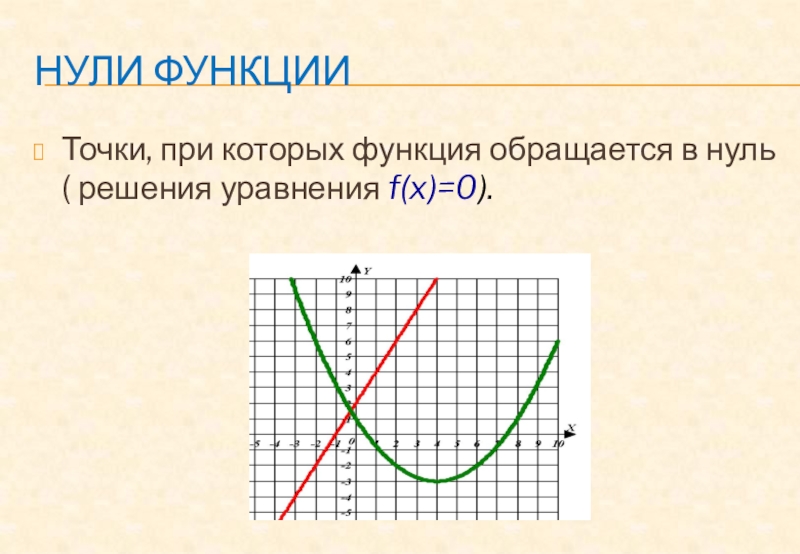
- 9. Нули функцииТочки, при которых функция обращается в нуль ( решения уравнения f(x)=0).
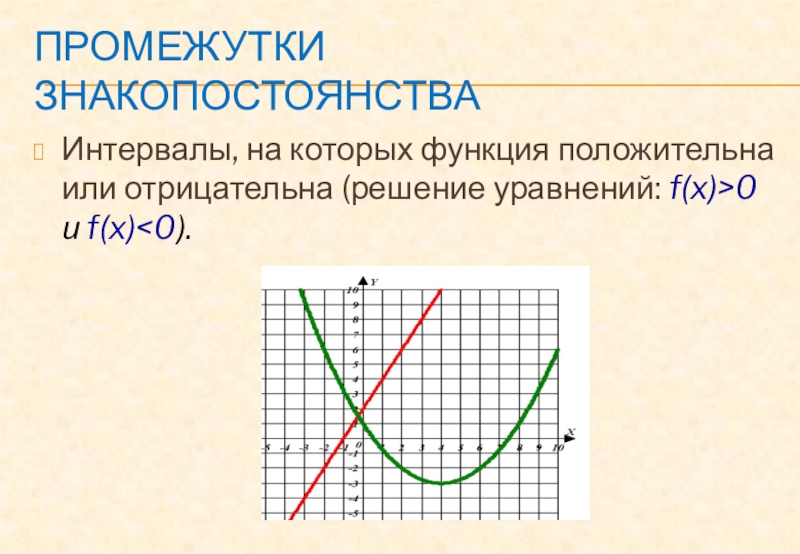
- 10. Промежутки знакопостоянстваИнтервалы, на которых функция положительна или отрицательна (решение уравнений: f(x)>0 и f(x)
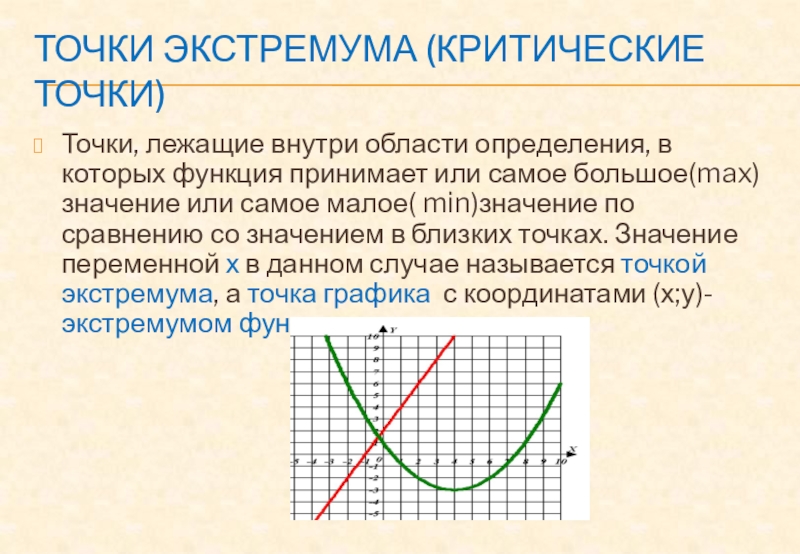
- 11. Точки экстремума (критические точки)Точки, лежащие внутри области
- 12. Свойства функции
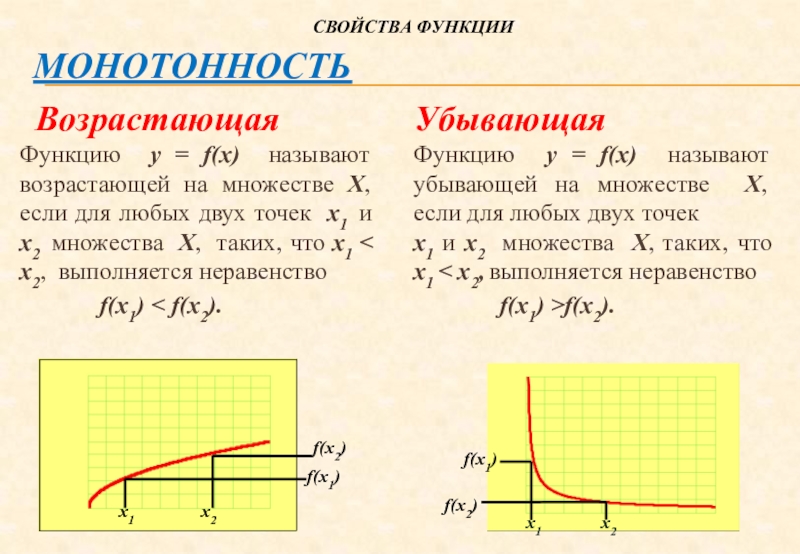
- 13. Монотонность ВозрастающаяФункцию у = f(х) называют
- 14. НепрерывностьНепрерывность функции на промежутке Х означает, что
- 15. Свойства функцииЧЕТНОСТЬЧетная функцияНечетная функцияФункция y = f(x)
- 16. ВыпуклостьФункция выпукла вниз
- 17. ОграниченностьФункцию у = f(х) называют ограниченной снизу
- 18. Наибольшее и наименьшее значенияЧисло m называют наименьшим
- 19. периодичностьФункция y = f (x)называется периодической, если
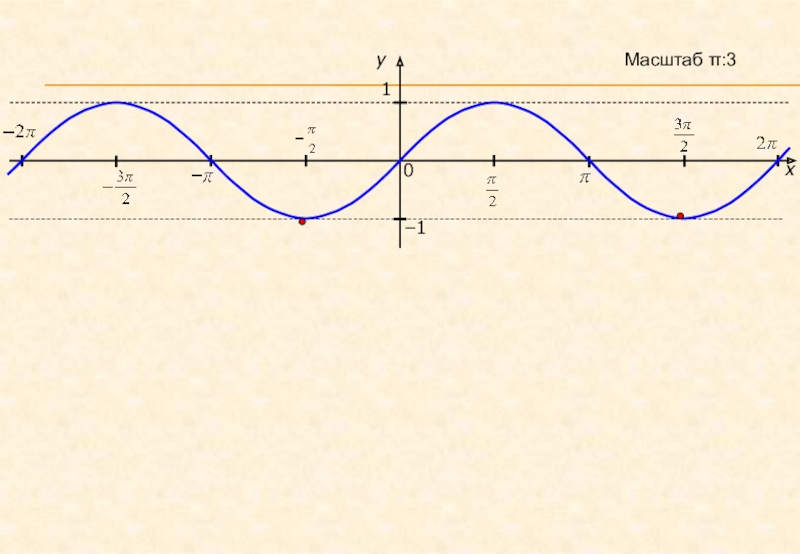
- 20. x10Масштаб :3−1y
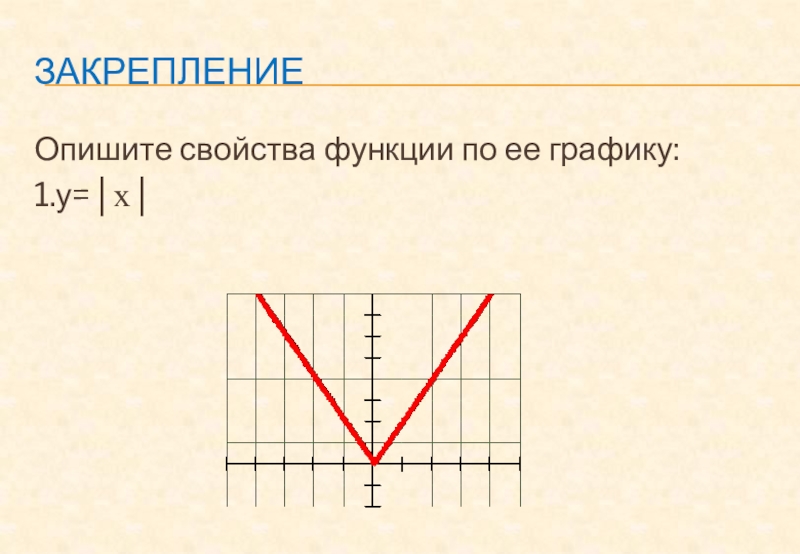
- 21. ЗакреплениеОпишите свойства функции по ее графику:1.у=│x│
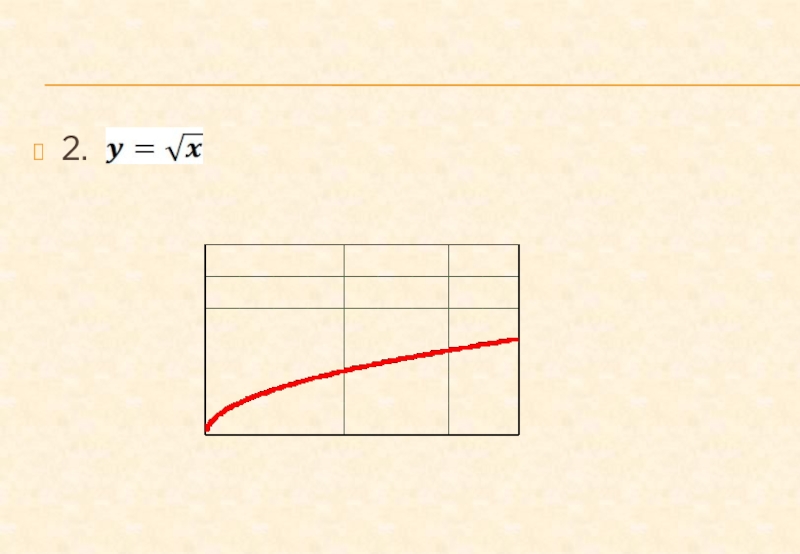
- 22. 2.
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
«Функция, ее свойства и график»
Учебное пособие по дисциплине
«Математика»
Преподаватель: Шевченко
О.А.
Слайд 2Переменные
Рене́ Дека́рт
1596 — 1650,
— французский математик,, создатель
аналитической геометрии и современной алгебраической символики
(Различные меняющиеся величины Т,V,p,I,U,S,t…..)
независимые
x
зависимые
y
Реальные
процессы связаны с большим количеством переменных и зависимостей между ними.Изучение зависимостей между переменными - наша главная задача.
Слайд 3Простейшие зависимости
1. Пропорциональная зависимость: у=кх, к- постоянное число.
График: прямая.
2.Обратно пропорциональная
зависимость: у=к/х, к- постоянное число, к≠0.
График: гипербола.
3.Квадратичная зависимость: у =
ах2 +bх+с.График: парабола.
Пример: I=U/R
Слайд 4Определение функции
Функция – это такая зависимость переменной у от переменной
х, при которой, по некоторому правилу, каждому значению х соответствует
одно единственное значение у.у есть функция от х.
Обозначают:
Переменная х называется независимой переменной или аргументом функции.
Переменная у называется зависимой переменной или функцией.
Слайд 5Способы задания функции:
Аналитический(формулами)
например:
Табличный
(на практике часто приходится пользоваться таблицами
значений функций, полученных опытным путём или в результате наблюдений)
Графический(задаётся
график функции).Слайд 6График функции
Графиком функции y = f(x) называется множество точек (х;
у) плоскости О х у, координаты которых связаны соотношением y
= f(x).Само равенство y = f(x) называется уравнением этого графика.
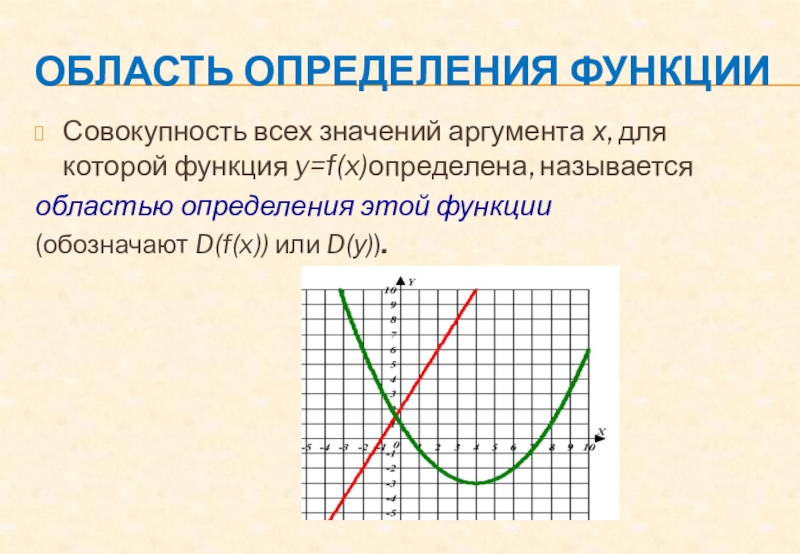
Слайд 7Область определения функции
Совокупность всех значений аргумента х, для которой функция
y=f(x)определена, называется
областью определения этой функции
(обозначают D(f(x)) или D(у)).
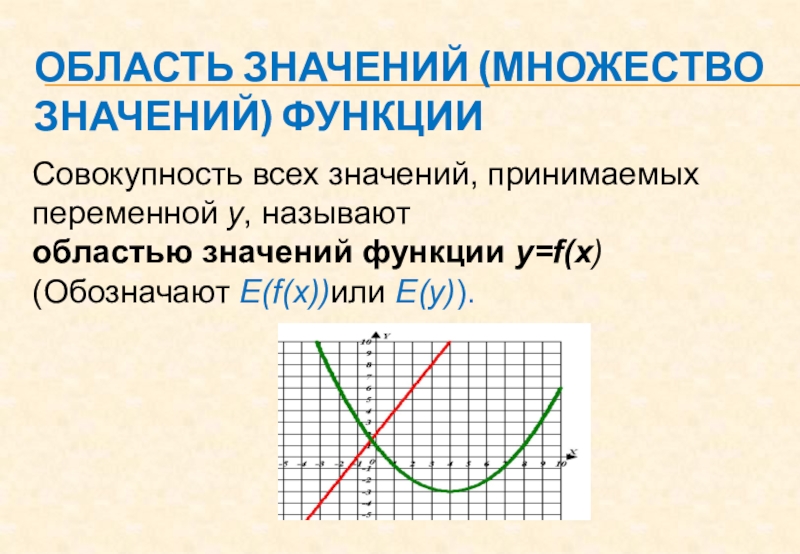
Слайд 8Область значений (множество значений) функции
Совокупность всех значений, принимаемых переменной у,
называют
областью значений функции y=f(x)
(Обозначают Е(f(x))или Е(у)).
Слайд 10Промежутки знакопостоянства
Интервалы, на которых функция положительна или отрицательна (решение уравнений:
f(x)>0 и f(x)
Слайд 11Точки экстремума (критические точки)
Точки, лежащие внутри области определения, в которых
функция принимает или самое большое(max) значение или самое малое( min)значение
по сравнению со значением в близких точках. Значение переменной х в данном случае называется точкой экстремума, а точка графика с координатами (х;у)- экстремумом функции.Слайд 13Монотонность
Возрастающая
Функцию у = f(х) называют возрастающей
на множестве Х, если для любых двух точек х1 и
х2 множества Х, таких, что х1 < х2, выполняется неравенствоf(х1) < f(х2).
Убывающая
Функцию у = f(х) называют убывающей на множестве Х, если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство
f(х1) >f(х2).
x1
x2
f(x1)
f(x2)
х1
x2
f(x2)
f(x1)
Свойства функции
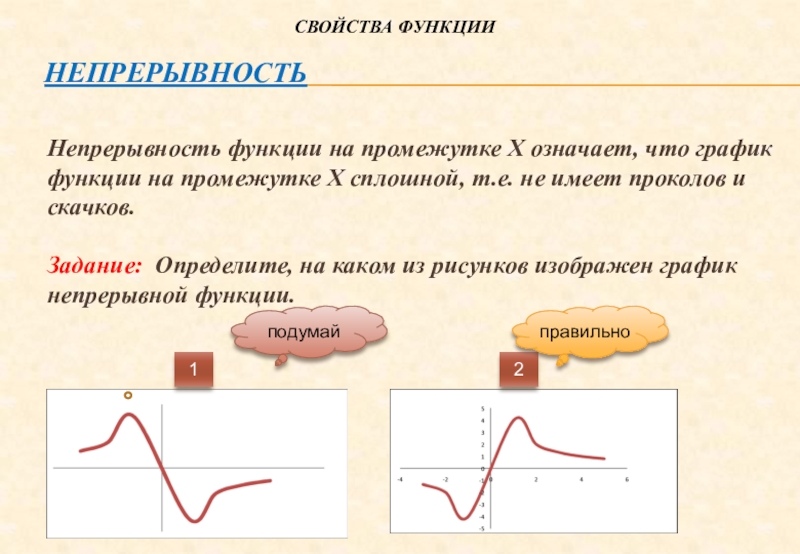
Слайд 14Непрерывность
Непрерывность функции на промежутке Х означает, что график функции на
промежутке Х сплошной, т.е. не имеет проколов и скачков.
Задание: Определите,
на каком из рисунков изображен график непрерывной функции.Свойства функции
1
2
подумай
правильно
Слайд 15Свойства функции
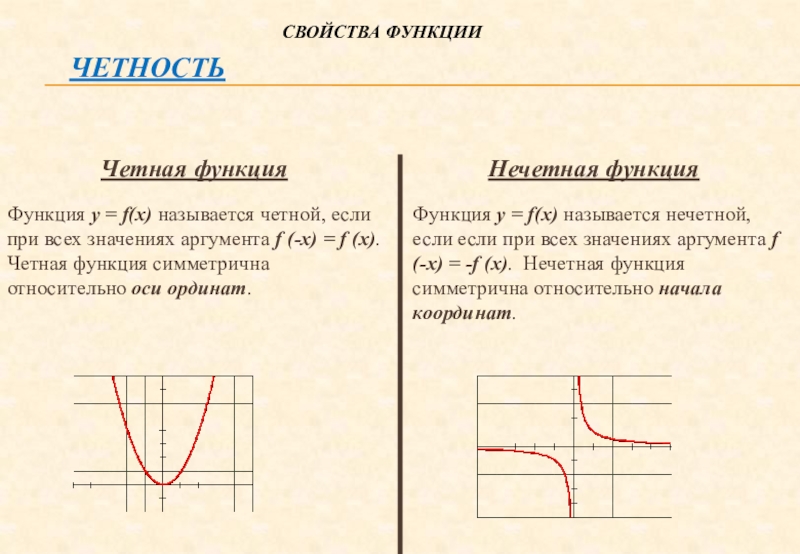
ЧЕТНОСТЬ
Четная функция
Нечетная функция
Функция y = f(x) называется четной, если
при всех значениях аргумента f (-x) = f (x). Четная
функция симметрична относительно оси ординат.Функция y = f(x) называется нечетной, если если при всех значениях аргумента f (-x) = -f (x). Нечетная функция симметрична относительно начала координат.
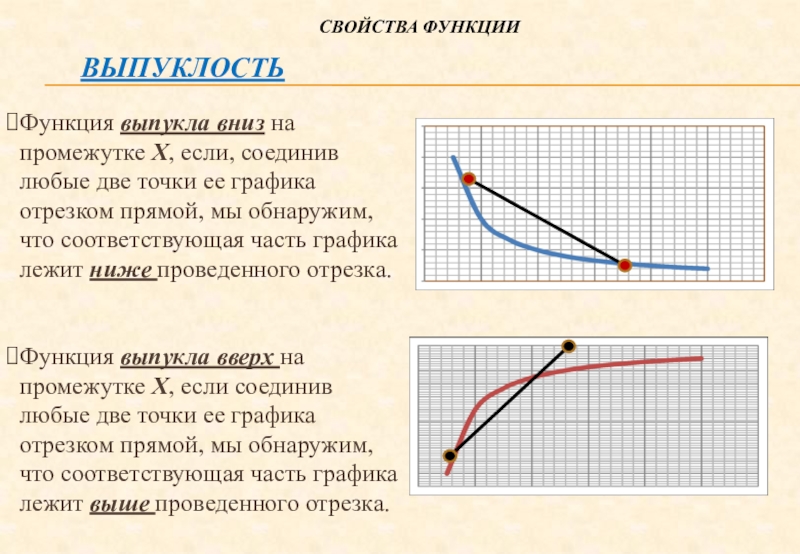
Слайд 16 Выпуклость
Функция выпукла вниз на промежутке Х,
если, соединив любые две точки ее графика отрезком прямой, мы
обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.Функция выпукла вверх на промежутке Х, если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
Свойства функции
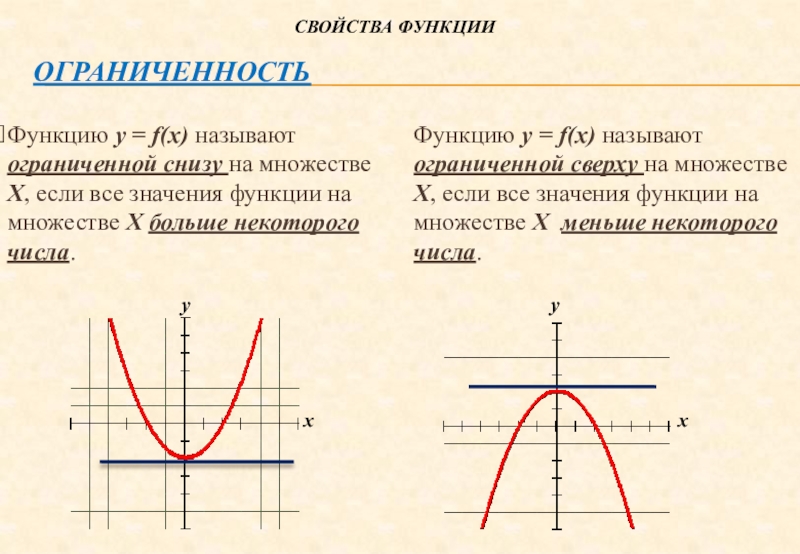
Слайд 17Ограниченность
Функцию у = f(х) называют ограниченной снизу на множестве Х,
если все значения функции на множестве Х больше некоторого числа.
Функцию
у = f(х) называют ограниченной сверху на множестве Х, если все значения функции на множестве Х меньше некоторого числа.х
у
х
у
Свойства функции
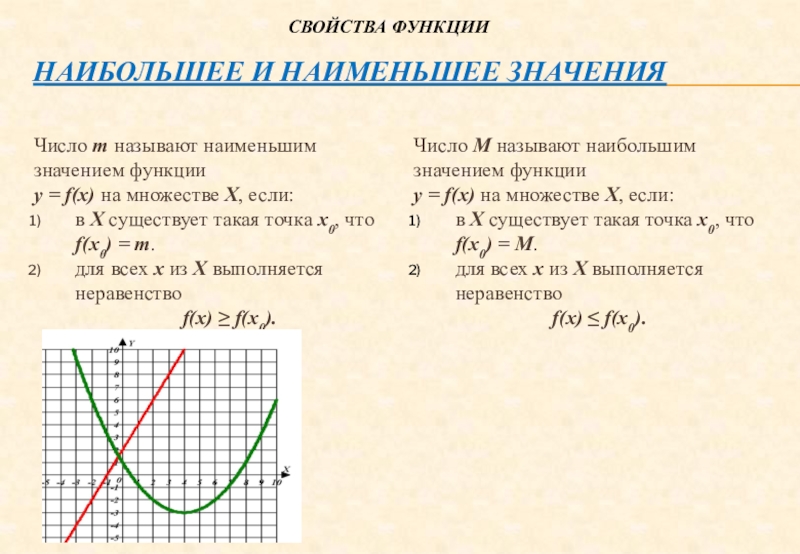
Слайд 18Наибольшее и наименьшее значения
Число m называют наименьшим значением функции
у
= f(х) на множестве Х, если:
в Х существует такая точка х0, что f(х0) = m.
для всех х из Х выполняется неравенство
f(х) ≥ f(х0).
Число M называют наибольшим значением функции
у = f(х) на множестве Х, если:
в Х существует такая точка х0, что f(х0) = M.
для всех х из Х выполняется неравенство
f(х) ≤ f(х0).
Свойства функции
Слайд 19периодичность
Функция y = f (x)называется периодической, если существует такое числоT≠0,
что для каждого х из области определения функции значения х
+ Т и х -Т также принадлежат её области определения, и при этом выполняются равенстваf ( x – T ) = f ( x ) = f ( x + T ).
Число Т называется
периодом функции y = f(x).