Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геострофическое равновесие
Содержание
- 1. Геострофическое равновесие
- 2. Полная система уравнений, которая, является достаточной для компьютерного моделирования атмосферы всех движений воздуха
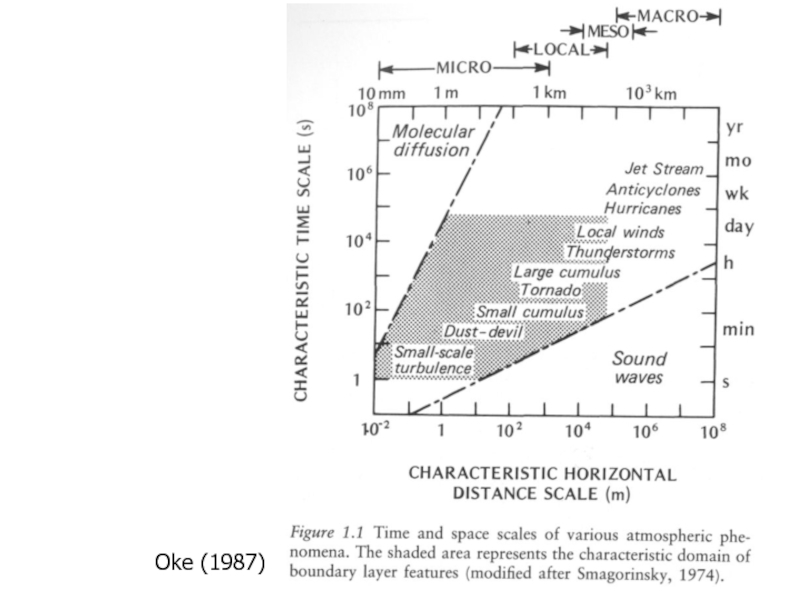
- 3. Lecture 01 - IntroductionOke (1987)
- 4. Характерные масштабы атмосферных движенийТрудности моделирования атмосферных процессов – следствиемногомасштабности движений
- 5. Уравнения преобразуются в дискретную форму, когда переменные
- 6. Для получения численной модели нужных движений применяется метод подобияГеометрическое подобиеДинамическое подобиеКинематическое подобиеТребования к моделированию
- 7. Геометрическое подобие представляет собой пропорциональность сходственных размеров
- 8. Невозможность геометрического подобия в геофизикеВ 2007 году
- 9. Кинематическое подобие означает пропорциональность местных скоростей в
- 10. Динамическое подобие – это пропорциональность сил, действующих
- 11. При теоретическом анализе выбирают постоянные масштабы моделируемых
- 12. Для выявления динамического подобия используют КРИТЕРИИ ПОДОБИЯКритерий
- 13. Слайд 13
- 14. Слайд 14
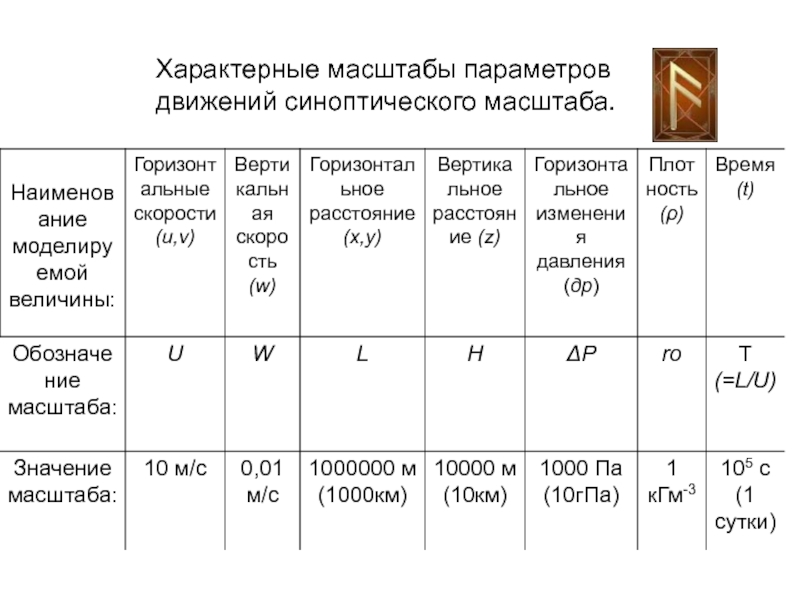
- 15. Характерные масштабы параметров движений синоптического масштаба.
- 16. Пример введения безразмерных переменных в определяющие уравненияЕсли
- 17. Анализ масштабов вертикального движения атмосферы движения атмосферы происходят квазистатически
- 18. Оценка порядков слагаемых в уравнении меридионального ускорения
- 19. Число Россби-Кибеля Ro=U/(lL)Это безразмерный комплекс, который
- 20. Роль числа RoПри одинаковой величине барического градиента
- 21. Основное равновесие атмосферы при синоптическом анализеВлияние молекулярной
- 22. Основные выводы:
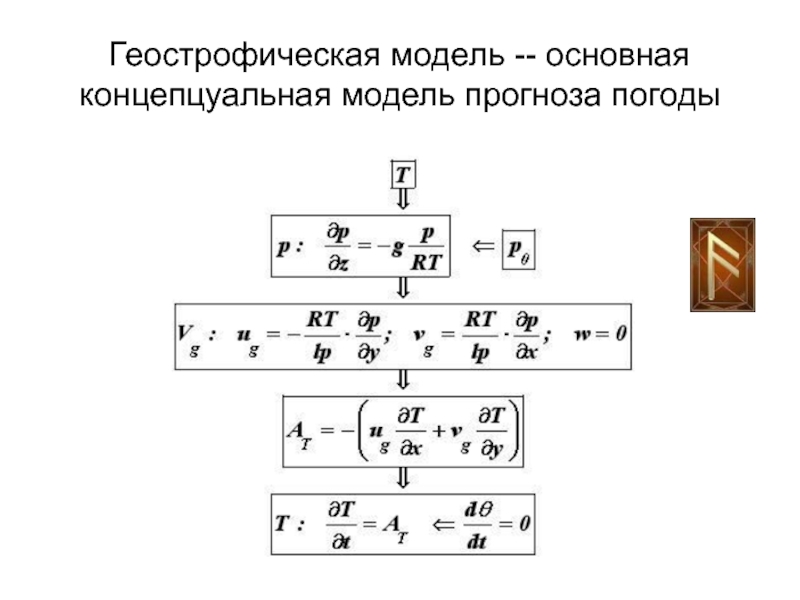
- 23. Геострофическая модель -- основная концепцуальная модель прогноза погоды
- 24. Геострофическое равновесиеИ его основные свойства
- 25. Разложение силы Кориолиса на горизонтальную и вертикальную составляющие
- 26. Геострофическое равновесиеЭто принятая векторная запись геострофического равновесия.Индексы ()s, указатели плоских векторов, обычно опускают!
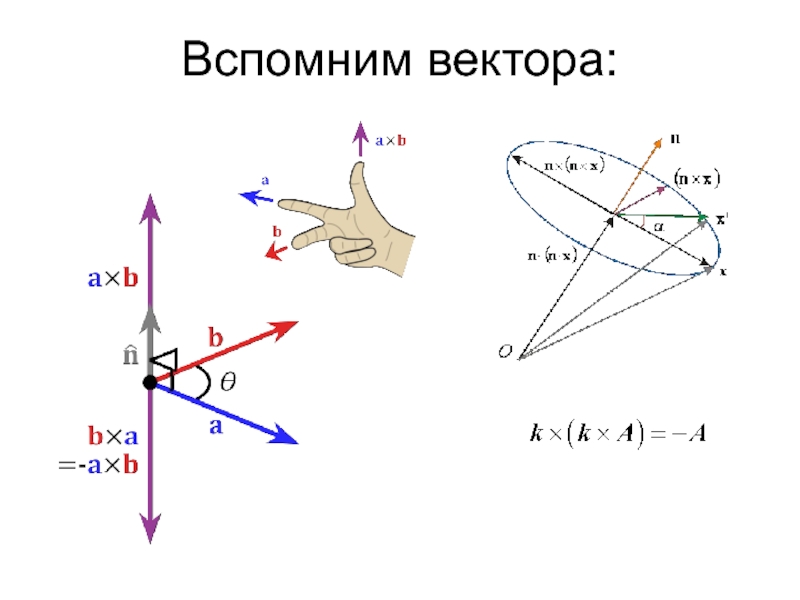
- 27. Вспомним вектора:
- 28. Решение векторного уравнения геострофического равновесияДля справки:
- 29. Задача: НАПРАВЛЕНИЕ геострофического ветраИспользуя правило правой руки,
- 30. Как векторное произведение, вектор направлен влево
- 31. Задача: а что меняется в южном полушарии?Ответ:
- 32. Задача: НАПРАВЛЕНИЕ геострофического ветраИспользуя правило правой руки,
- 33. Зачем он нужен ?В свободной атмосфере (выше
- 34. Способ оценки.Рабочая формула для вычисления модуля скорости геострофического ветраПример оценки величины скорости геострофического ветра:
- 35. Геострофический ветер не может быть определен на
- 36. Уравнения геострофического баланса у экватора имеют видОтсюда
- 37. Геострофического ветра в изобарической системе координат
- 38. Изменение геострофического ветра с высотой между изобарическими поверхностями– этот вектор называется « термический ветер»
- 39. Термический ветер в лабораторииМы заполняем цилиндрический резервуар
- 40. Запомнить!Изменение вектора геострофического ветра с высотой выражается
- 41. Пример термического ветра 1: объяснение струйного
- 42. Смотри рисунок!
- 43. Пример термического ветра 2: Наклон фронтальных зон в атмосфере
- 44. Оценка угла наклона фронта и изобарической поверхностиДля
- 45. БаротропностьЕсли температура горизонтально однородна, то горизонтальный барический
- 46. Математическое выражение баротропности плоскопараллельного потока Если якобиан давления и плотности равен нулю, то поток баротропен
- 47. БароклинностьЕсли температура горизонтально НЕОДНОРОДНА, то горизонтальный барический
- 48. Математическое выражение бароклинности плоскопараллельного потока В атмосфере
- 49. Слайд 49
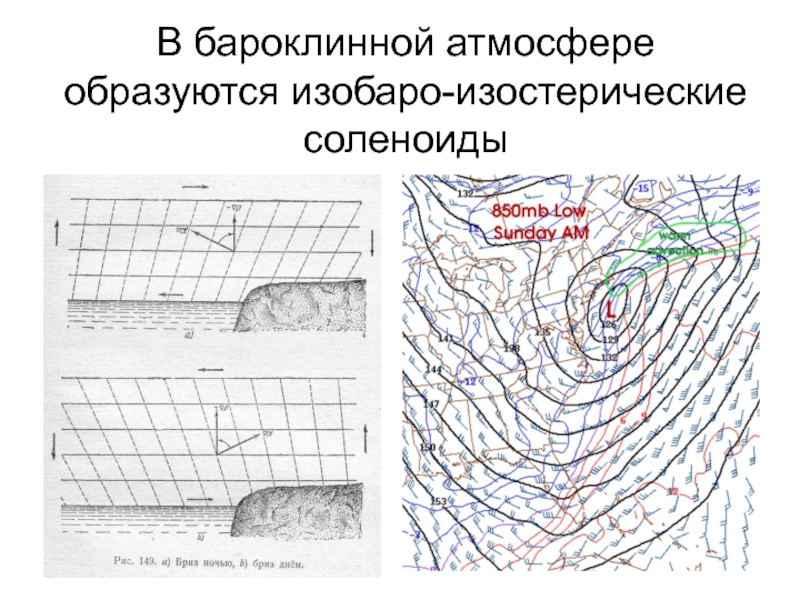
- 50. В бароклинной атмосфере образуются изобаро-изостерические соленоиды
- 51. Адвекции температурыВеличина АT называется в метеорологии адвективным
- 52. Геострофическая адвекция температуры выражается через поворот ветра с высотой
- 53. Геострофическая адвекция температуры При повороте геострофического ветра
- 54. Геострофическая адвекция температуры (а значит и термический
- 55. Геострофическая адвекция и и спиральность геострофического потока (забежим вперед)Спиральность ветра пропорциональна геострофической адвекции температуры
- 56. Память о войне:Возрастание α с высотой есть
- 57. Скачать презентанцию
Полная система уравнений, которая, является достаточной для компьютерного моделирования атмосферы всех движений воздуха
Слайды и текст этой презентации
Слайд 2Полная система уравнений, которая, является достаточной для компьютерного моделирования атмосферы
всех движений воздуха
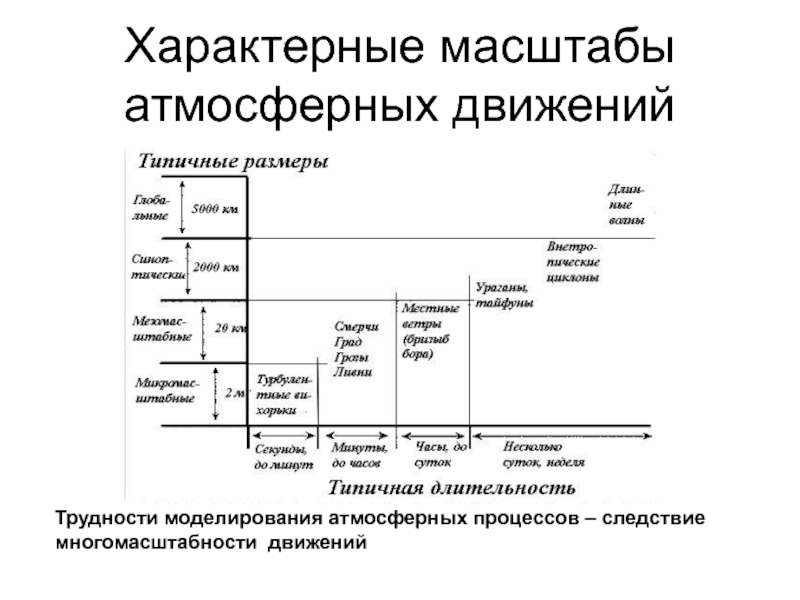
Слайд 4Характерные масштабы атмосферных движений
Трудности моделирования атмосферных процессов – следствие
многомасштабности движений
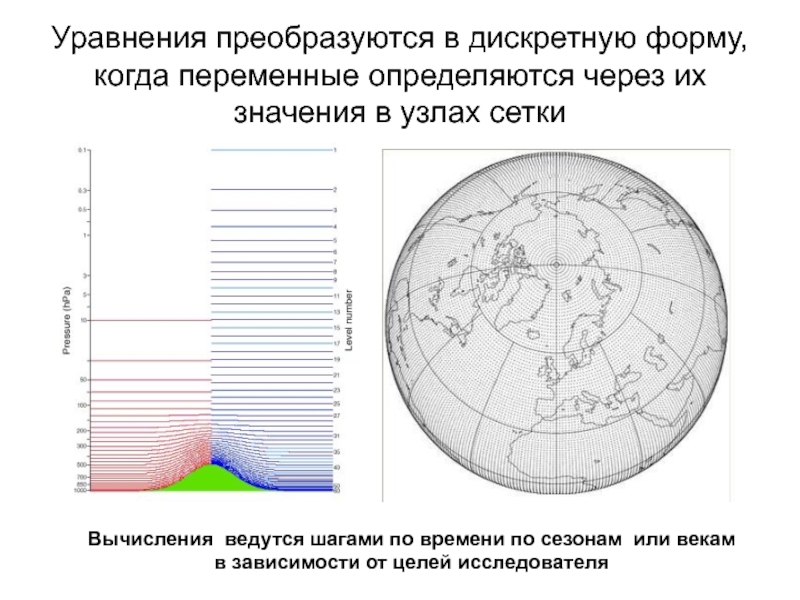
Слайд 5Уравнения преобразуются в дискретную форму, когда переменные определяются через их
значения в узлах сетки
Вычисления ведутся шагами по времени по сезонам
или векам в зависимости от целей исследователя
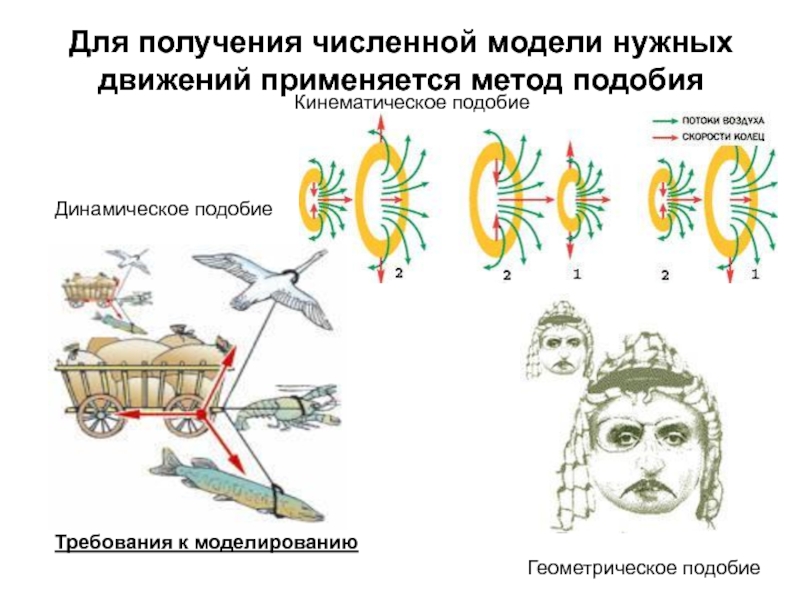
Слайд 6Для получения численной модели нужных движений применяется метод подобия
Геометрическое подобие
Динамическое
подобие
Кинематическое подобие
Требования к моделированию
Слайд 7
Геометрическое подобие представляет собой пропорциональность сходственных размеров и равенство соответствующих
углов.
Под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают
потоки
Слайд 8Невозможность геометрического подобия в геофизике
В 2007 году рабочие Дорогобужского химического
завода решили сделать из старого ГАЗГОЛЬДЕРА глобус. Получился самый большой
глобус в Европе (больше только в Нью-Йорке). Дорогобужский глобус достигает в высоту 12 метров, диаметра — 10,5 метра, вес 12 тонн, располагается на шести столбах в метре над землей. Шар расписывали профессиональные смоленские художники под началом руководителя проекта, известного дизайнера Михаила Шведова, который и задумал сделать его географической картой мира. Слой атмосферы до 30 км (тропосфера и стратосфера) над этим глобусом представлял бы собой пленку толщиной 2,5 см.
Слайд 9Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и
равенство углов, характеризующих направление этих скоростей
Из кинематического подобия вытекает
геометрическое подобие линий тока. Очевидно, что для кинематического подобия требуется геометрическое подобие русел. 
Слайд 10Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы
в кинематически подобных потоках и равенство углов, характеризующих направление этих
сил.В потоках жидкостей обычно действуют разные силы: силы давления, вязкости (трения), тяжести и др.
Соблюдение их пропорциональности означает полное гидродинамическое подобие.
Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором соблюдается пропорциональность лишь основных, главных сил.
Слайд 11При теоретическом анализе выбирают постоянные масштабы моделируемых переменных.
При выборе масштаба
обычно принимают, что в модели значения масштабируемой величины не должны
существенно отличаться от единицы.Например, если в реальных условиях составляющая скорости u может меняться от нуля (штиль) до 40 м/с (ураганный ветер), то выбрав в качестве масштаба значение U=10 м/с, можно ожидать,
что аналогичная составляющая в модели um , будет безразмерной и меняющейся от нуля до 4, так как в условиях кинематического подобия должны выполняться равенства.
Слайд 12Для выявления динамического подобия используют КРИТЕРИИ ПОДОБИЯ
Критерий подобия– это отношение
двух множителей порядка в определяющем уравнении
Критерий подобия — безразмерная величина,
составленная из размерных физических параметров, определяющих рассматриваемое физическое явлениеРавенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие физического подобия этих систем
Слайд 16Пример введения безразмерных переменных в определяющие уравнения
Если разделить все члены
уравнения на один из множителей порядка, то можно получить безразмерное
уравнение с коэффициентами, которые называют критериями подобия
Слайд 17Анализ масштабов вертикального движения атмосферы
движения атмосферы происходят квазистатически
Слайд 18Оценка порядков слагаемых в уравнении меридионального ускорения путем сравнения с
ускорением Кориолиса.
Параметр Кориолиса
Для оценки поверхностных сил принята гипотеза Ньютона
Слайд 19 Число Россби-Кибеля Ro=U/(lL)
Это безразмерный комплекс, который позволяет оценить, какой
из факторов компенсируют воздействие силы барического градиента
относительное ускорение частицы воздуха
или ускорение Кориолиса
Слайд 20Роль числа Ro
При одинаковой величине барического градиента балансирующие его ускорения
могут быть различными для движений с разным горизонтальным масштабом L.
При L ≈ 1000 км и Ro< 1 выполняется баланс, который называется геострофическим равновесием. Но если рассматриваются процессы, у которых L ≈ 100 км, то Ro≈1 и баланс градиентным равновесием.
Для процессов еще меньшего масштаба L ≈ 10 км и менее уже Ro>1 и главным становиться баланс между барическим градиентом и относительным ускорением.
(В зарубежной литературе этот случай иногда называют циклострофическим равновесием).
Слайд 21Основное равновесие атмосферы при синоптическом анализе
Влияние молекулярной вязкости на эти
потоки несущественно.
Главными динамическими факторами являются сила барического градиента и сила
Кориолиса.С относительной ошибкой около 10% можно использовать уравнения горизонтального движения синоптического масштаба в виде
Слайд 26Геострофическое равновесие
Это принятая векторная запись геострофического равновесия.
Индексы ()s, указатели плоских
векторов, обычно опускают!
Слайд 29Задача: НАПРАВЛЕНИЕ геострофического ветра
Используя правило правой руки, убедиться, что геострофический
ветер направлен в северном полушарии влево от градиента давления, а
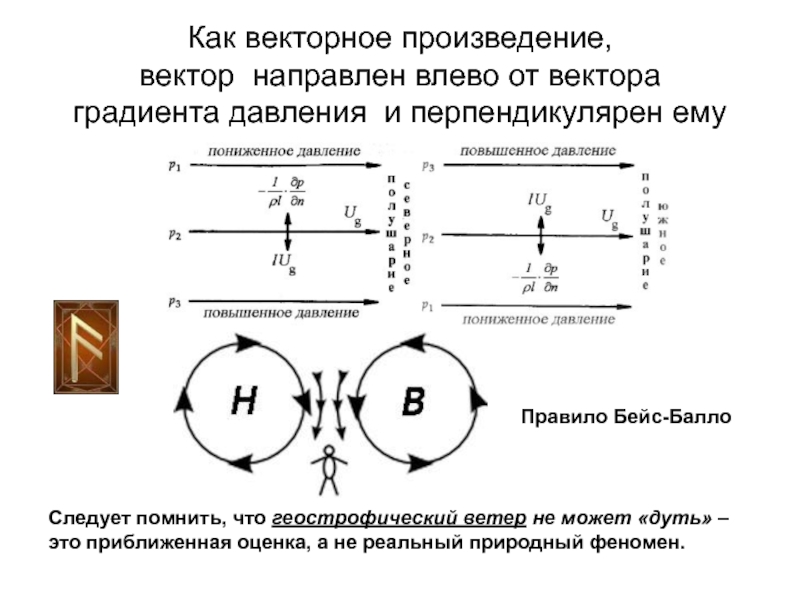
значит по отношению к изобарам в соответствие с законом Бейс-Балло
Слайд 30Как векторное произведение, вектор направлен влево от вектора градиента давления
и перпендикулярен ему
Следует помнить, что геострофический ветер не может
«дуть» – это приближенная оценка, а не реальный природный феномен. Правило Бейс-Балло
Слайд 31Задача: а что меняется в южном полушарии?
Ответ: единичный вектор вертикали
–к там будет иметь направление противоположное вектору угловой скорости вращения
землиПоэтому разложение угловой скорости будет иметь вид
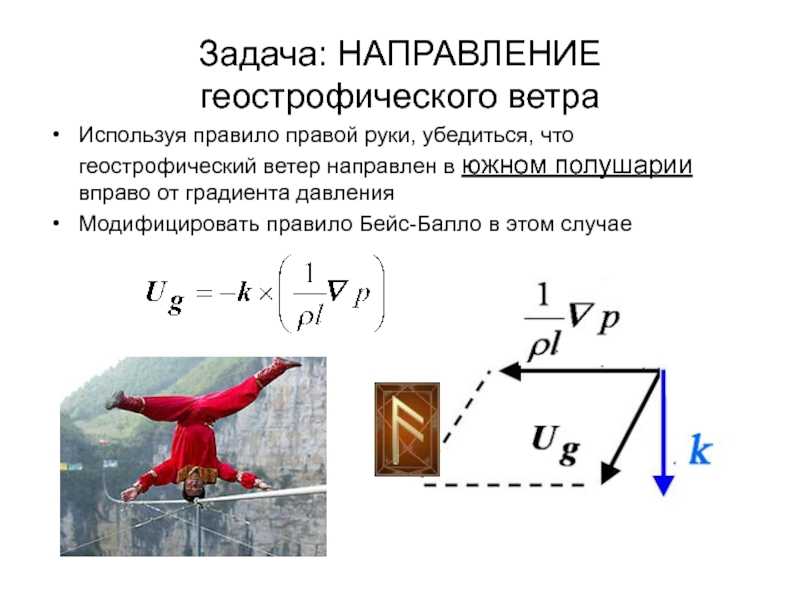
Слайд 32Задача: НАПРАВЛЕНИЕ геострофического ветра
Используя правило правой руки, убедиться, что геострофический
ветер направлен в южном полушарии вправо от градиента давления
Модифицировать правило
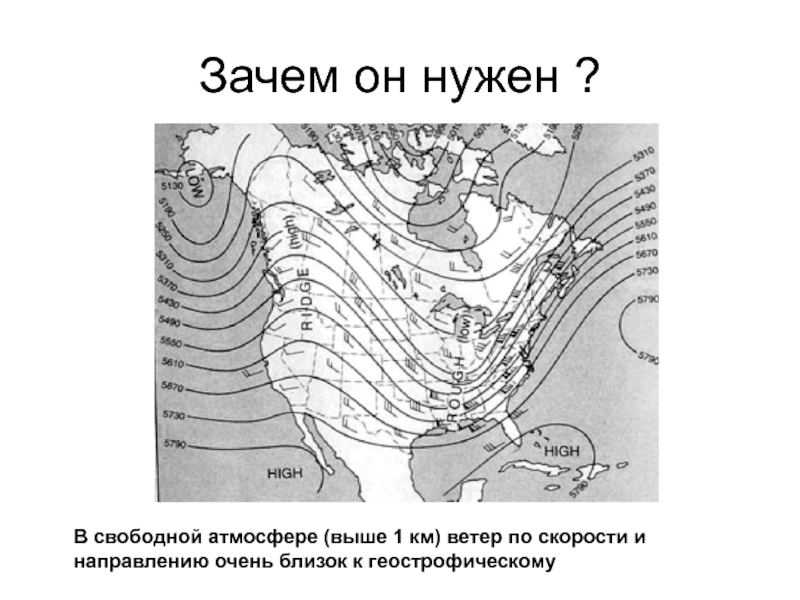
Бейс-Балло в этом случае
Слайд 33Зачем он нужен ?
В свободной атмосфере (выше 1 км) ветер
по скорости и направлению очень близок к геострофическому
Слайд 34Способ оценки.
Рабочая формула для вычисления модуля скорости геострофического ветра
Пример оценки
величины скорости геострофического ветра:
Слайд 35Геострофический ветер не может быть определен на экваторе!
Расположение осей стандартной
системы координат на экваторе
Вектор угловой скорости вращения Земли в
этой стандартной системе координат имеет вид .Вектор силы Кориолиса имеет компоненты
Слайд 36Уравнения геострофического баланса у экватора имеют вид
Отсюда следует, что
аналогом
геострофического потока у экватора будет движение в вертикальном направлении,
при
условии образования вдоль экватора экстремума барического поля. Рассчитать горизонтальные скорости по этим равенствам невозможно.
Поэтому говорят, что геострофический ветер у экватора не определим.
Слайд 37Геострофического ветра
в изобарической системе координат
Переход к изобарической системе
координат
Высота изобарической поверхности p=const – теперь стала функцией : z(t,x,y,p)
Слайд 38Изменение геострофического ветра с высотой
между изобарическими поверхностями
– этот вектор
называется « термический ветер»
Слайд 39Термический ветер в лаборатории
Мы заполняем цилиндрический резервуар водой (глубина 15
см), и вращаем его очень медленно - не более чем
в 0,8 об / мин (или даже меньше) в против часовой стрелки.В центре мы размещаем оловянный цилиндр 15 см в диаметре со льдом. Оставляем на 20 минут для установления. Затем кидаем
нескольких кристаллов марганцовки. Они падают вертикально на дно. Полосы не остаются вертикальными: они наклоняются в азимутальном направлении все сильнее с увеличением высотой от дна. Мы посыпаем кусочки черной бумаги на поверхность и они движутся в том же направлении, но быстрее, чем, вращается стол (суперротация).
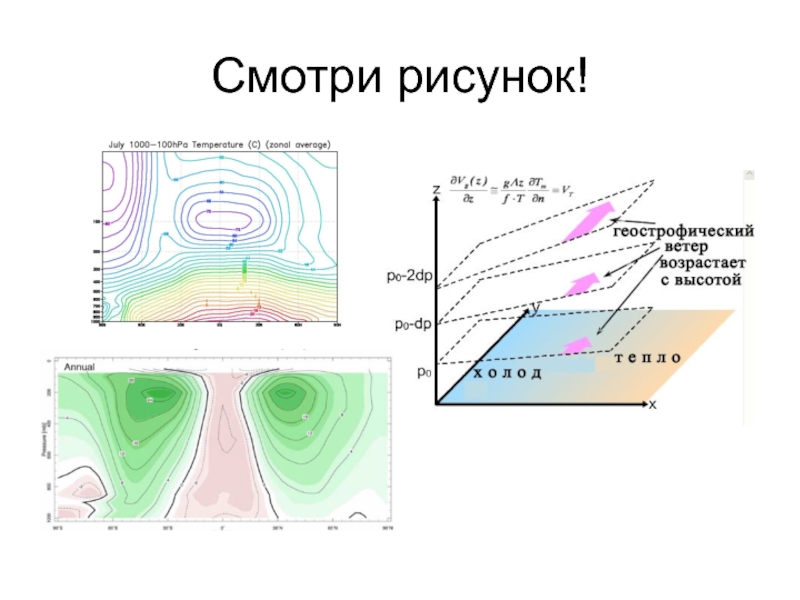
Слайд 40Запомнить!
Изменение вектора геострофического ветра с высотой выражается как в увеличение
скорости, так и в изменении направления.
Вектор термического ветра, перпендикулярен
термическому градиенту т.е. «дует» вдоль изотерм средней температуры слоя от p1 до p2Квази Бейс-Балло: термический ветер «дует» вдоль изотерм так, чтобы (если встать к нему спиной), слева оказывалась область холода (в северном полушарии)
Слайд 41Пример термического ветра 1:
объяснение струйного течения
В широтной зоне от
30 до 40 N зональный градиент температуры в тропосфере достигает
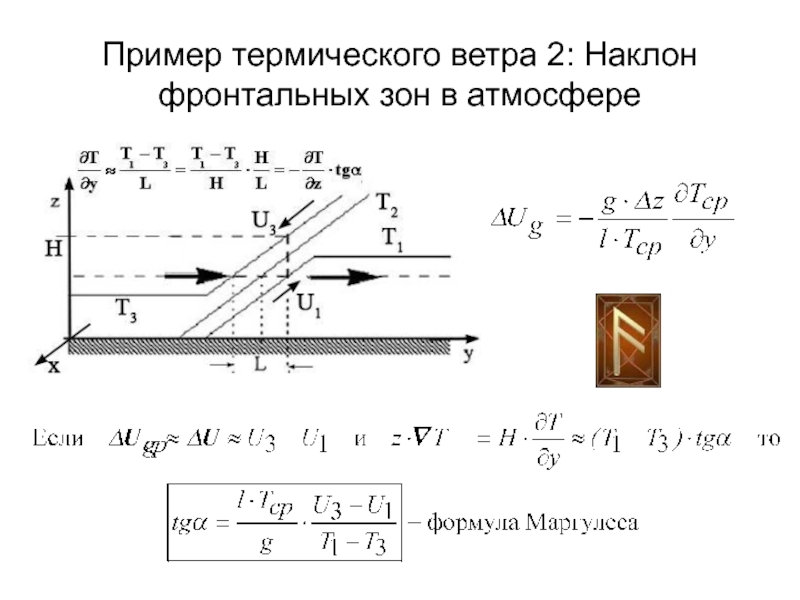
200С/1000 км. Задать недостающие параметры и оценить скорость ветра на высоте 8 км. (U(0)=0)
Слайд 44Оценка угла наклона фронта и изобарической поверхности
Для фронта
U3-U1=10[м/с], Т3=273К, Т1=283К,
Тср=278К
Тогда tgα= lTср/g = 0.0036 (=0.20) при ϕ=450
Для изобаричесой поверхности:
dp=pxdx+pzdz=0
откуда tgβ=dz/dx=-px/pz=(ρlV/ρg)=0.00013=(0.00740)
Хотя оба угла очень малы, но
tgα / tgβ = 28
Т.е. если изобару изображать под углом 10 к горизонтали, то фронт следует изобразить под углом 300 к горизонтали
![Оценка угла наклона фронта и изобарической поверхностиДля фронтаU3-U1=10[м/с], Т3=273К, Т1=283К, Тср=278КТогда tgα= lTср/g = 0.0036 (=0.20) при](/img/thumbs/0a66cafd49ab318a11ffa39b3d16f9a5-800x.jpg "Геострофическое равновесие Оценка угла наклона фронта и изобарической поверхностиДля фронтаU3-U1=10[м/с], Т3=273К, Т1=283К, Тср=278КТогда")
Слайд 45Баротропность
Если температура горизонтально однородна, то горизонтальный барический градиент зависит только
от изменений плотности. Это легко доказать с помощью уравнения состояния
В
этом случае (реки) изобарические поверхности должны быть параллельны изостерическим (поверхностям постоянной плотности). Такое состояние является баротропным.
В этом случае термический ветер ОТСУТСТВУЕТ!
Слайд 46Математическое выражение баротропности плоскопараллельного потока
Если якобиан давления и плотности
равен нулю, то поток баротропен
Слайд 47Бароклинность
Если температура горизонтально НЕОДНОРОДНА, то горизонтальный барический градиент зависит от
изменений плотности и температуры. Это легко доказать с помощью уравнения
состоянияВ этом случае (атмосфера, океан) изобары поверхности не должны совпадать с изотермами по направлению( на одной и той же изобарической поверхности).
Такое состояние является бароклинным.
При нем термический ветер обязательно существует
Это значит, что изменение вектора ветра с высотой является признаком бароклинности атмосферы.
Слайд 48Математическое выражение бароклинности плоскопараллельного потока
В атмосфере якобиан давления и
плотности пропорционален якобиану давления и температуры. Если изобары и изотермы
не параллельны, он не равер нулю, т.е. атмосфера бароклинна!
Слайд 51Адвекции температуры
Величина АT называется в метеорологии адвективным изменением температуры или
адвекцией температуры
Если АT >0, то воздух в выбранном пункте
нагревается. В этом случае говорят об адвекции тепла. Если АT < 0, то воздух в выбранном пункте охлаждается. В этом случае говорят об адвекции холода.
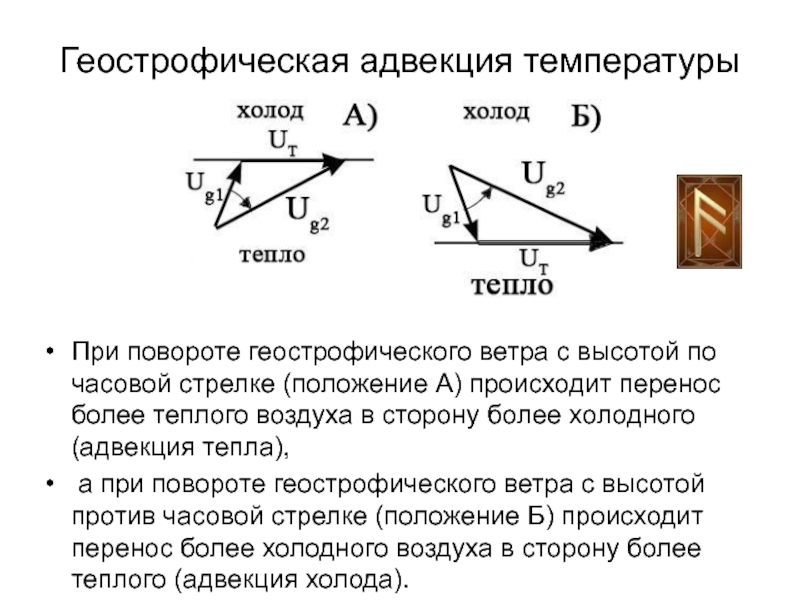
Слайд 53Геострофическая адвекция температуры
При повороте геострофического ветра с высотой по
часовой стрелке (положение А) происходит перенос более теплого воздуха в
сторону более холодного (адвекция тепла),а при повороте геострофического ветра с высотой против часовой стрелке (положение Б) происходит перенос более холодного воздуха в сторону более теплого (адвекция холода).
Слайд 54Геострофическая адвекция температуры (а значит и термический ветер!) выражает бароклинность
атмосферы
Чем сильнее ветер меняет направление с высотой, тем сильнее бароклинность
атмосферы
Слайд 55Геострофическая адвекция и и спиральность геострофического потока (забежим вперед)
Спиральность ветра
пропорциональна геострофической адвекции температуры
Слайд 56Память о войне:
Возрастание α с высотой есть поворот ветра против
часовой стрелки (влево), т.е. свидетельство адвекции холода.
Убывание α с высотой
есть поворот ветра по часовой стрелки (вправо), т.е. свидетельство адвекции тепла. 
