Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГЛАВА I. МЕХАНИКА §§2 ‒3. Кинематика
Содержание
- 1. ГЛАВА I. МЕХАНИКА §§2 ‒3. Кинематика
- 2. §2. Кинематика материальной точкиI. Закон движенияКинематика —
- 3. §2. Кинематика материальной точкиII. Системы координат 1. Декартова система координатДлина (модуль, абсолютная величина) радиуса-вектора
- 4. §2. Кинематика материальной точки2. Сферическая система координатφ
- 5. §2. Кинематика материальной точки3. Цилиндрическая система координатСвязь
- 6. III. Кинематические параметры1. ПеремещениеПеремещение (смещение) — приращение
- 7. Для того чтобы найти уравнение траектории, нужно
- 8. Средняя путевая скорость§2. Кинематика материальной точки
- 9. Обратная задачаДано , найтиЗа малое время dt
- 10. Мгновенное ускорениеОбратная задачаДано , найти— начальный радиус-вектор, — начальная скорость §2. Кинематика материальной точки
- 11. Пример решения обратной задачи1) Равномерное движение:2) Равноускоренное
- 12. ρ — радиус кривизны траекторииПри Δt → 0aτ —
- 13. I. Виды движенияПоступательное движение — движение, при
- 14. II. Угловые кинематические параметры1. Угловое перемещениеВектор углового
- 15. [φ] = рад (радиан)2. Угловая скоростьУгловая скорость
- 16. 4. Частота вращенияЧастота вращения — скалярная положительная
- 17. III. Связь между линейными и угловыми кинематическими
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ГЛАВА I. МЕХАНИКА
§§2‒3. Кинематика
О. И. Лубенченко
НИУ МЭИ
Кафедра физики им. В.
А. Фабриканта
Слайд 2§2. Кинематика материальной точки
I. Закон движения
Кинематика — раздел механики, изучающий
механическое движение без рассмотрения его причин.
Радиус-вектор материальной точки — вектор,
соединяющий начало отсчёта и материальную точку.Кинематический закон движения материальной точки (закон движения):
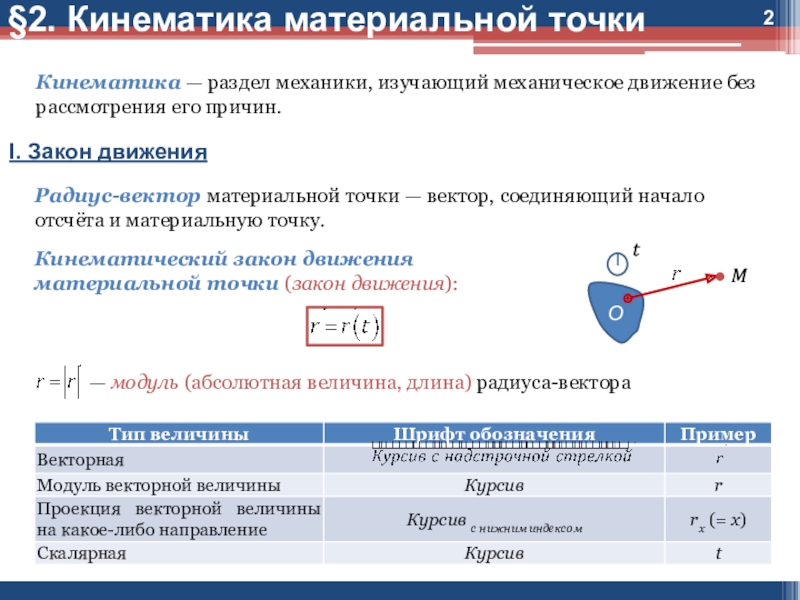
Слайд 3§2. Кинематика материальной точки
II. Системы координат
1. Декартова система координат
Длина (модуль,
абсолютная величина) радиуса-вектора
Слайд 4§2. Кинематика материальной точки
2. Сферическая система координат
φ — азимутальный угол,
θ — полярный угол
Связь сферических координат с декартовыми:
Слайд 5§2. Кинематика материальной точки
3. Цилиндрическая система координат
Связь цилиндрических координат с
декартовыми:
Частный случай: полярная система координат (при z = 0)
Результат решения задачи
не должен зависеть от выбора системы координат!Слайд 6III. Кинематические параметры
1. Перемещение
Перемещение (смещение) — приращение радиуса-вектора.
Траектория. Уравнение траектории
Траектория
материальной точки — кривая, описываемая точкой при её движении.
§2. Кинематика
материальной точки[r] = м
Путь ΔS — длина участка траектории.
Δr ≠ ΔS!
Слайд 7Для того чтобы найти уравнение траектории, нужно исключить время из
кинематического закона движения в координатной форме:
(для двумерного движения)
2. Скорость
Скорость —
векторная ФВ, характеризующая быстроту движения.Средняя скорость
Δt = t2 – t1
Мгновенная скорость
Вектор мгновенной скорости направлен по касательной к траектории.
§2. Кинематика материальной точки
Слайд 9Обратная задача
Дано , найти
За малое время dt материальная точка совершает
перемещение
Просуммируем все малые перемещения, т. е. проведём интегрирование по времени:
— начальный
радиус-вектор3. Ускорение
Ускорение — векторная ФВ, характеризующая скорость изменения скорости материальной точки.
Среднее ускорение
§2. Кинематика материальной точки
Слайд 10Мгновенное ускорение
Обратная задача
Дано , найти
— начальный радиус-вектор, — начальная скорость
§2. Кинематика
материальной точки
Слайд 11Пример решения обратной задачи
1) Равномерное движение:
2) Равноускоренное движение:
IV. Криволинейное движение
Орты
естественной системы координат
— единичный вектор, направленный по касательной к траектории
по направлению движения— единичный вектор, направленный по нормали к траектории в сторону её вогнутости
§2. Кинематика материальной точки
Слайд 12ρ — радиус кривизны траектории
При Δt → 0
aτ — тангенциальное (касательное) ускорение
an
— нормальное (центростремительное) ускорение
§2. Кинематика материальной точки
Слайд 13I. Виды движения
Поступательное движение — движение, при котором любая прямая,
соединяющая две точки движущегося тела, перемещается параллельно самой себе.
Вращение вокруг
неподвижной оси (вращательное движение) — движение, при котором все точки тела движутся по окружностям, лежащим в параллельных плоскостях, таким, что центры этих окружностей лежат на одной прямой, называемой осью вращения.Плоское движение — движение, при котором все точки тела движутся в параллельных плоскостях.
Плоское движение = поступательное движение + вращательное движение.
Сферическое движение (вращение вокруг неподвижной точки) — движение, при котором все точки тела движутся по сферам, центры которых находятся в одной точке, называемой центром вращения.
Другие случаи – сложное движение.
§3. Кинематика твёрдого тела
Слайд 14II. Угловые кинематические параметры
1. Угловое перемещение
Вектор углового перемещения для малых
угловых перемещений
Направление — по правилу правого винта.
Угол φ — скалярная
ФВ, характеризующая поворот тела.Закон вращательного движения твёрдого тела
§3. Кинематика твёрдого тела
Слайд 15[φ] = рад (радиан)
2. Угловая скорость
Угловая скорость — векторная ФВ,
характеризующая быстроту и направление вращения.
3. Угловое ускорение
Угловое ускорение — векторная
ФВ, характеризующая быстроту и направление изменения угловой скорости.При вращении вокруг неподвижной оси
§3. Кинематика твёрдого тела
Слайд 164. Частота вращения
Частота вращения — скалярная положительная ФВ, характеризующая быстроту
вращения, равная числу оборотов тела вокруг оси вращения за единичный
промежуток времени.5. Период вращения
Период вращения — скалярная положительная ФВ, характеризующая быстроту вращения, равная времени, за которое вращающееся тело совершает один полный оборот вокруг оси вращения.
§3. Кинематика твёрдого тела













![ГЛАВА I. МЕХАНИКА §§2 ‒3. Кинематика [φ] = рад (радиан)2. Угловая скоростьУгловая скорость — векторная ФВ, характеризующая [φ] = рад (радиан)2. Угловая скоростьУгловая скорость — векторная ФВ, характеризующая быстроту и направление вращения.3. Угловое ускорениеУгловое](/img/tmb/6/581819/cb1978245f2895bf39f28dfa43ed4752-800x.jpg)