Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Группа команд Скретч Перо Разработала : Лобанова Т.К. педагог ДО ГБОУ ЦДО
Содержание
- 1. Группа команд Скретч Перо Разработала : Лобанова Т.К. педагог ДО ГБОУ ЦДО
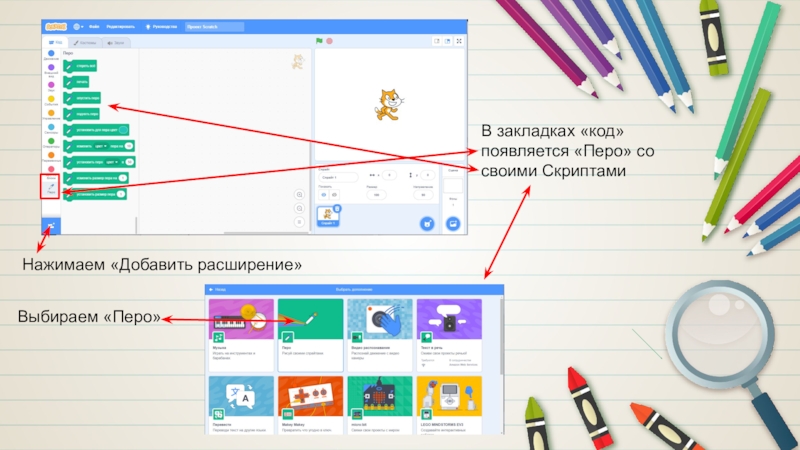
- 2. Нажимаем «Добавить расширение»Выбираем «Перо»В закладках «код» появляется «Перо» со своими Скриптами
- 3. Перо есть в запасе у каждого исполнителя-спрайта.
- 4. - Установите Кота на сцене мышкой.- Произвольно поверните исполнителя
- 5. Можно получать интересные картинки, если поворачивать квадрат
- 6. Если вращать вокруг центра прямую, она
- 7. Вспомним, что окружность состоит из точек
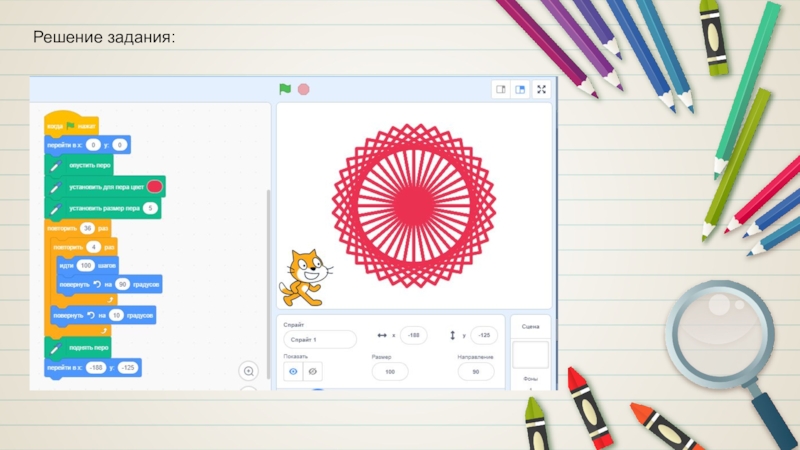
- 8. Решение задания:
- 9. Правильным считается такой многоугольник, у которого
- 10. Попробуйте нарисовать: окружность, правильные фигуры со
- 11. Слайд 11
- 12. Скачать презентанцию
Нажимаем «Добавить расширение»Выбираем «Перо»В закладках «код» появляется «Перо» со своими Скриптами
Слайды и текст этой презентации
Слайд 2Нажимаем «Добавить расширение»
Выбираем «Перо»
В закладках «код» появляется «Перо» со своими
Скриптами
Слайд 3Перо есть в запасе у каждого исполнителя-спрайта.
Оно расположено точно
в его центре.
И если дать команду Опустить перо, спрайт при
своём движении, будет оставлять след на сцене. Всё очень просто!
Составить процедуру рисования квадрата со стороной 100.
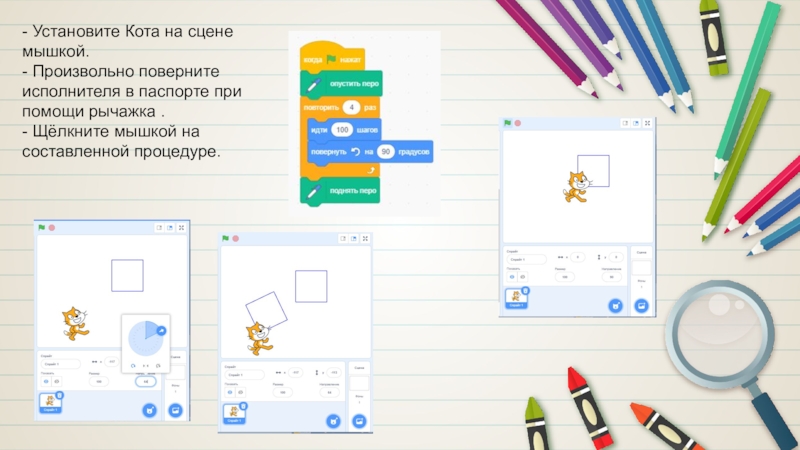
Слайд 4- Установите Кота на сцене мышкой.
- Произвольно поверните исполнителя в паспорте при
помощи рычажка .
- Щёлкните мышкой на составленной процедуре.
Слайд 5Можно получать интересные картинки, если поворачивать квадрат вокруг одной из
своих вершин.
Соберите программу, которая рисует такие узоры.
Слайд 6 Если вращать вокруг центра прямую, она опишет полный круг, повернувшись
на 360°. На такой угол можно повернуть и квадрат, поворачивая его 36 раз
по 10°.Для установки нужного цвета щёлкните на цветном квадратике в блоке команды
а затем на подходящем цвете в окне приложения, например, на красной кнопке.
В этом скрипте использована, написанная ранее, процедура Квадрат.
Для проверки щёлкнем мышкой на зелёном флажке .
Слайд 7
Вспомним, что окружность состоит из точек удалённых на одинаковое расстояние
от одной точки, называемой центром окружности.
Все точки окружности, в том числе
точки A и B, удалены на одно и то же расстояние r от центра окружности O. Отрезок, соединяющий точку на окружности с центром, называют радиусом окружности.
Когда квадрат вращается вокруг своей вершины O, эта вершина становится центром окружности, а две другие соседние вершины движутся по окружности с радиусом, равным стороне квадрата r, а диагональ крадрата ОС по большой окружности..
Слайд 9
Правильным считается такой многоугольник, у которого все стороны равны между
собой и все углы равны между собой. На рисунке представлены
правильные: треугольник, четырёхугольник (квадрат), пятиугольник, шестиугольник, восьмиугольник и десятиугольникВ сумме все повороты составляют 360°!
Так как углы всех поворотов равны, то получается, что для построения N-угольника нужно после прорисовки каждой стороны поворачиваться на угол равный 360/N.
Получаем универсальный алгоритм построения правильного N-угольника.
Алгоритм:
1. Повторить N раз:
2. Рисуем сторону
3. Поворачиваемся на 360/N°
Команды можно дублировать (копировать), нажав на правую
кнопку мышки.
Слайд 10
Попробуйте нарисовать:
окружность,
правильные фигуры со стороной 100:
треугольник,
квадрат,
пятиугольник,
шестиугольник,
восьмиугольник.
Для каждой фигуры выберите свой цвет пера и свою клавишу
запуска Скрипта.Решение сохранить под именем
Многоугольники.
