Характеристики звеньев систем автоматики 1. Динамические характеристики. 2

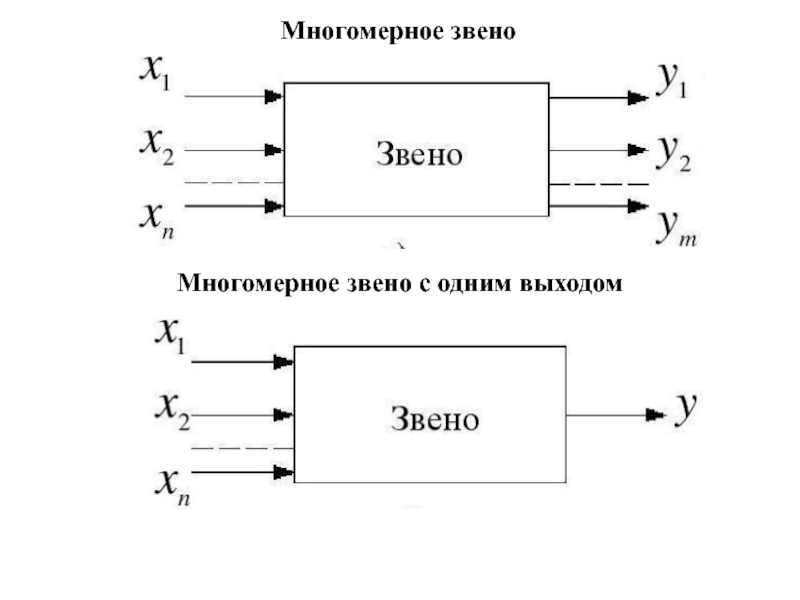
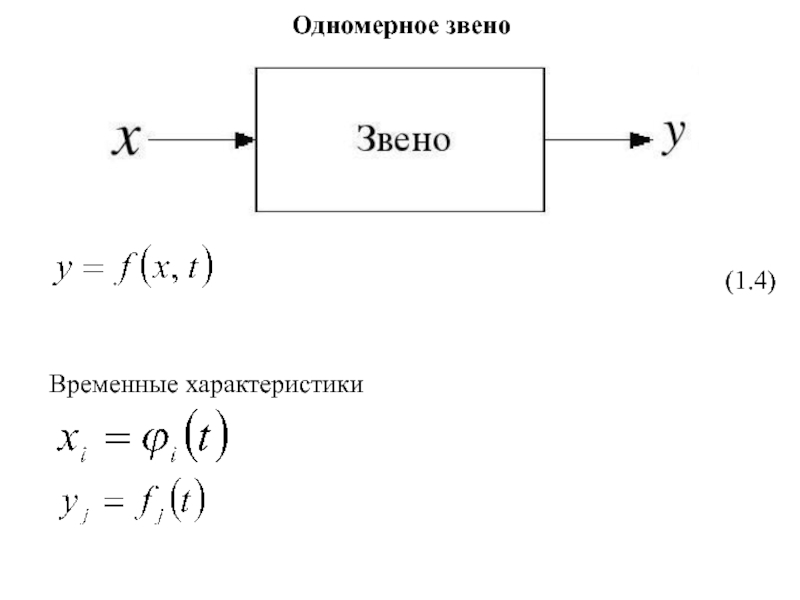
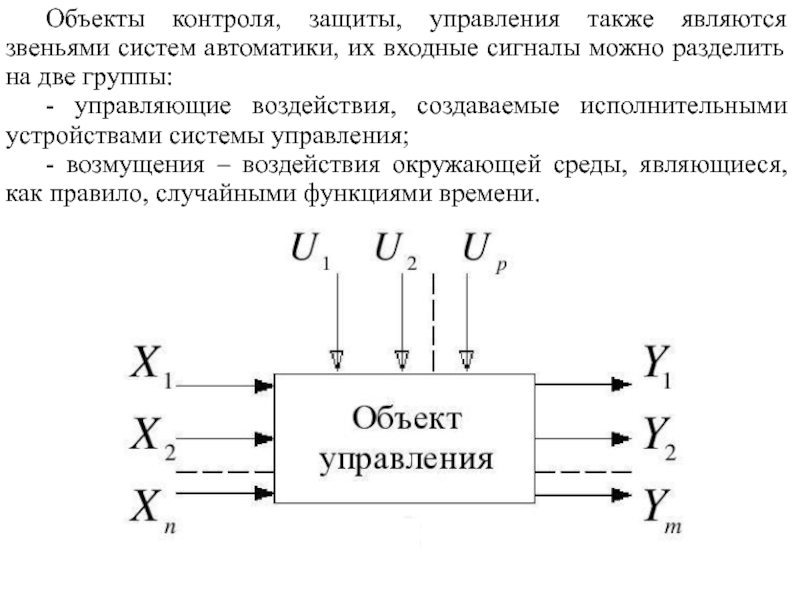
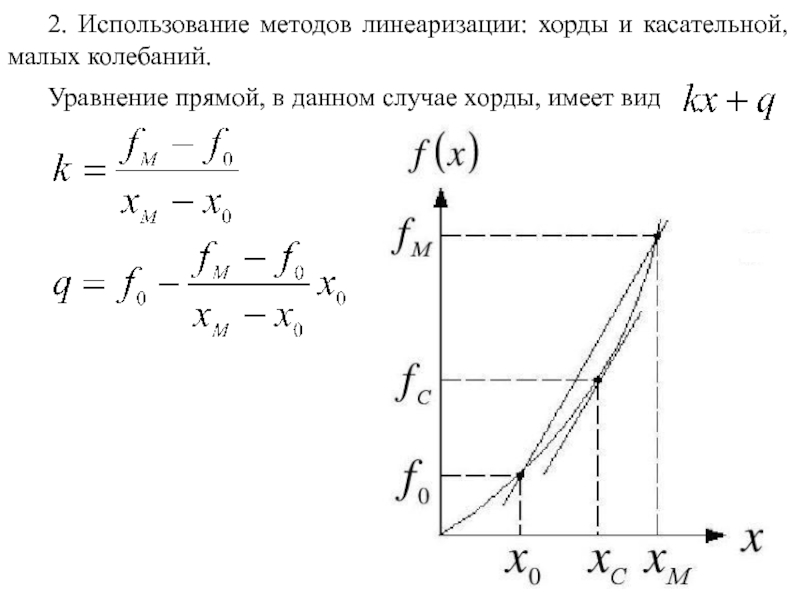
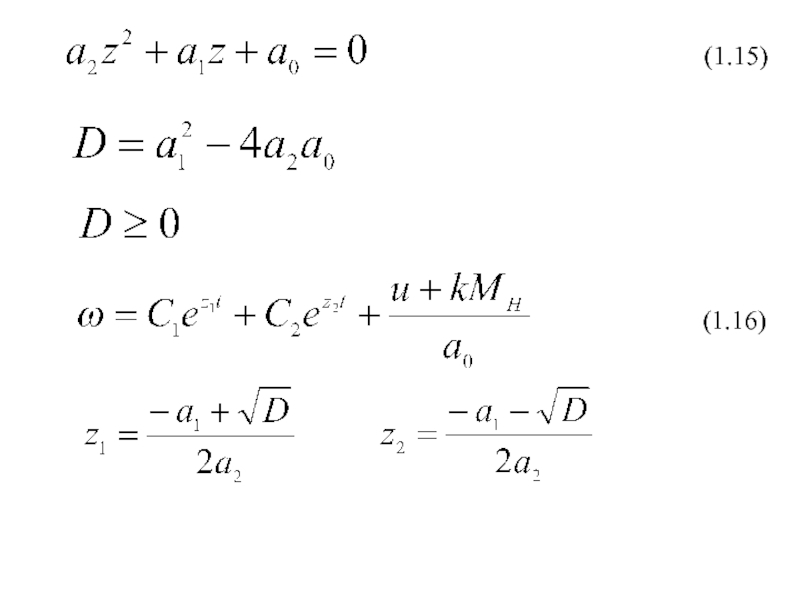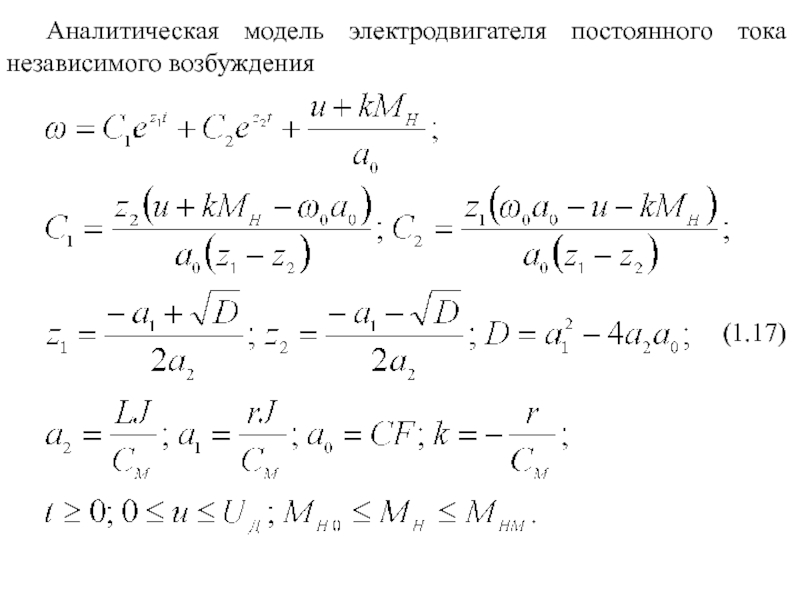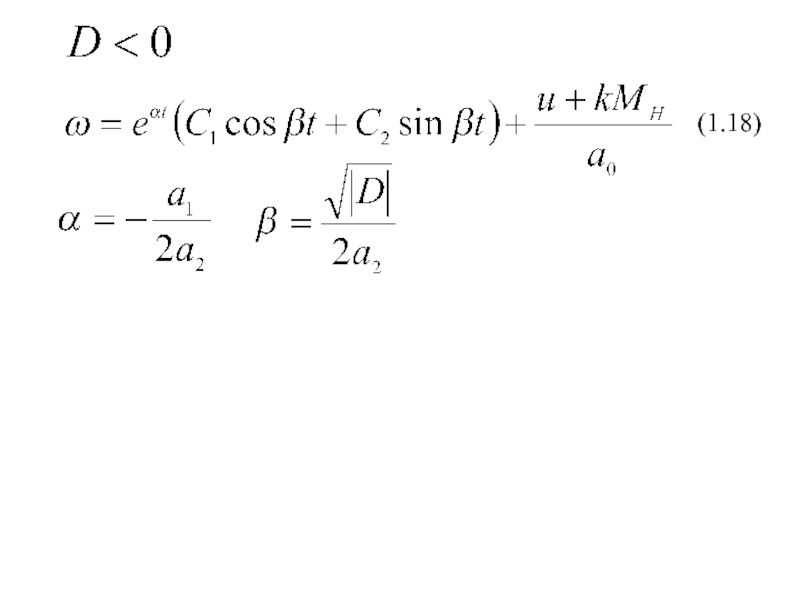4. Линейные и нелинейные звенья.
5. Преобразования Лапласа.
6. Передаточная функция.
7. Переходная

характеристика.
8. Импульсная характеристика.
9. Частотные характеристики.
10. Типовые динамические звенья.
11. Статические характеристики.
12. Дискретные звенья.

одного параметра от другого. Зависимость одного параметра от другого можно

также выразить аналитически в виде формулы или нескольких формул, по которым легко получить графическое или табличное выражение данной зависимости.
Характеристика звена системы автоматики – зависимость выходного сигнала звена от входных, или зависимость выхода от входов.

При функционировании систем автоматики в большинстве случаев сигналы изменяются во времени, причем изменения входных сигналов (входов) приводят к изменению выходных сигналов (выходов), но последние изменяются не мгновенно, а с течением времени. Такой режим работы звена называется динамическим. Зависимость выходного сигнала звена y от входных

и от времени t называется динамической характеристикой звена.

(1.3)

входные сигналы можно разделить на две группы:
- управляющие воздействия, создаваемые

исполнительными устройствами системы управления;
- возмущения – воздействия окружающей среды, являющиеся, как правило, случайными функциями времени.

состояния объекта контроля, которые измеряются (наблюдаются), называют контролируемыми параметрами.
Переменные состояния

объекта управления, которые в процессе управления надо изменять по заданному закону, поддерживать неизменными или в определенном интервале называются управляемыми параметрами.

(1.5)

(1.6)

пример: звено состоит из терморезистора, включенного в цепь постоянного тока

последовательно с обычным резистором, выход звена – сила тока I (А), входы: напряжение U (В) и переменное сопротивление терморезистора R (Ом).
Сила тока, напряжение и эквивалентное сопротивление цепи связаны законом Ома

Так как терморезистор и обычный резистор включены в цепь последовательно, то эквивалентное сопротивление

математической (аналитической) модели звена, основой которой является полученная аналитическая зависимость.

Математическая модель звена также включает неравенства, выражающие ограничения входов:

(1.7)

Процесс разработки математической модели называется математическим моделированием.
Если звено не описывается известными физическими законами, аналитическими зависимостями, то установить характеристики звена можно проведением эмпирического исследования звена или структурным моделированием звена с последующей реализацией полученной математической модели звена на компьютере.

звене, так и на физической модели звена. Эмпирическое исследование выполняют

в соответствии с заранее разработанным планом, оно предусматривают измерения и регистрацию (запись) значений входов звена и соответствующих им значений выходов, при этом значения входов могут задаваться. Далее производиться математическая обработка результатов. Таким образом, устанавливаются характеристики звена в численном (табличном) виде, по ним можно построить графические или регрессионные зависимости выходов от входов. Процесс построения регрессионных зависимостей называется аппроксимацией. Построение математической модели на основе аппроксимации результатов эмпирического исследования называется функциональным моделированием.
Как правило, регрессионные зависимости представляются в виде полиномов. При одном входе x регрессионная зависимость выглядит следующим образом

(1.8)

математического описания отдельных частей звена. Звено рассматривается как система, состоящая

из взаимодействующих подсистем. Подсистемы выделяют таким образом, чтобы их можно было описать известными физическими законами, аналитическими зависимостями.
Рассмотрим пример: звено электродвигатель постоянного тока независимого возбуждения, выход звена – угловая скорость вращения вала, входы звена: напряжение, подаваемое в цепь якоря, момент нагрузки (сопротивления) на валу электродвигателя.
Электродвигатель – электромеханическая система, в которой можно выделить две подсистемы: электрическую – цепь якоря; механическую – вращающаяся часть, включающая вал электродвигателя, расположенные на нем элементы и вращающиеся части приводимого оборудования.

Ньютона для вращательного движения твердого тела
(1.11)

является имитационной, она предусматривает нереверсивную работу электродвигателя, если электродвигатель работает

реверсивно, то ограничение напряжения питания цепи якоря имеет вид

моделей. Реализация имитационной модели на компьютере называется имитационным моделированием, она

позволяет установить характеристики звена.
Если из уравнения (1.12) выразить параметр i и результат подставить в уравнение (1.10), то получим неоднородное линейное обыкновенное дифференциальное уравнение (ОДУ) второго порядка с постоянными коэффициентами

(1.14)

имеет вид:
(1.19)

моделирование системы автоматики – разработка математической модели системы автоматики путем

определения уравнений и аналитических зависимостей, связывающих входы и выходы звеньев, входящих в систему, преобразования уравнений и зависимостей, установления ограничений входов системы.

звенья систем автоматики делятся на две группы:
- линейные;
- нелинейные.
Линейные звенья

описываются линейными дифференциальными уравнениями, или дифференциальными уравнениями, которые посредством введения допущений можно привести к линейным. Нелинейные звенья описываются квазилинейными и нелинейными дифференциальными уравнениями.
Линейные дифференциальные уравнения решаются как аналитически, так и численными методами на компьютерах. Для установления характеристик и оценки свойств нелинейных звеньев используют методы исследования нелинейных систем.

следующим образом
(1.20)

в линеаризуемых функциях могут быть незначимыми, то есть пренебрежение ими

не приводит к искажениям значений функции. Например, напряжение на выходе потенциометра является функцией перемещения ползунка d

(1.22)

Если принять допущение, что

При малых значениях y можно принять
Применение допущений представляет собой простую математическую операцию, но оно может быть реализовано в редких случаях.

в данном случае хорды, имеет вид

k следует определить как среднее арифметическое из значений угловых коэффициентов

хорды и касательной, а свободный член q – как среднее арифметическое из значений свободных членов хорды и касательной.

мало отклоняется от некоторого заданного значения
Заданному значению выхода соответствуют определенные

входы:

Отклонения входов и выхода:

и y

Входы и выход в динамическом
режиме:

решений линейных дифференциальных уравнений и оценки устойчивости линейных САУ.
Оригиналы и

изображения функций по Лапласу

для суммы некоторых функций равно сумме преобразований Лапласа для отдельных

функций.
Изображение по Лапласу для производной функции равно

При нулевых начальных условиях, когда в момент времени t=0 выход и все его производные равны нулю, изображения для производных первой, второй, третьей

функции без вычисления ее оригинала:
(1.23)
Нулевые начальные условия: при

производится следующим образом.
1. К

уравнению применить прямое преобразование Лапласа, то есть привести его к виду уравнения (1.24).
2. Вынести за скобки изображения выхода ys и входа xs,, то есть привести к виду уравнения (1.25).
3. Вместо xs в правой части подставить изображение функции

по Лапласу, то есть .

к дроби с полиномами в числителе и знаменателе. В результате

получается в правой части некоторая функция F(s), а уравнение имеет вид

6. Функцию F(s) представить в виде суммы табличных функций f(s), то есть

7. К функции F(s) применить обратное преобразование Лапласа, а так как к обратному преобразованию Лапласа также применим принцип суперпозиции, то следует применить обратные преобразования Лапласа к функциям

которые заменяются

на оригиналы

Решение имеет вид

к изображению по Лапласу функции входа xs при нулевых начальных

условиях называется: передаточная функция

(1.26)

Передаточная функция

(1.27)

Передаточная функция зависит только от внутренних свойств звена и не зависит от состояния входа.

Вид передаточной функции определяется видом исходного дифференциального уравнения. Для линейного дифференциального уравнения передаточная функция представляет собой отношение двух полиномов.

звена. Звено с n входами и m выходами имеет

(m х n) передаточных функций. Одномерное звено имеет одну передаточную функцию. Объект управления (контроля) для каждого управляемого (контролируемого) параметра имеет передаточные функции по управляющим воздействиям и возмущениям.

рассматриваемом примере является объектом управления, применим к нему прямое преобразование

Лапласа (индекс s означает изображение функции по Лапласу)

(1.28)

Передаточная функция по управляющему воздействию

Передаточная функция по возмущению

(1.29)