Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Игры с природой
Содержание
- 1. Игры с природой
- 2. Понятие игры с природойМатричная игра, где игрок
- 3. Неопределенность Лицу, принимающему решение известен лишь набор
- 4. Матрица последствийЕсли будет принято i-e решение, а
- 5. Матрица сожалений (рисков)Допустим, мы хотим оценить риск,
- 6. Критерий Лапласа (критерий безразличия)
- 7. Максимаксный критерий (критерий крайнего оптимизма)Максимаксный (минимаксный) критерий
- 8. Правило Вальда (крайнего пессимизма) Рассматривая i-e решение,
- 9. Правило СэвиджаКритерий Сэвиджа стремится смягчить консерватизм минимаксного
- 10. Правило ГурвицаПри любом выборе стратегии наихудший для
- 11. Пример 1 В приближении посевного сезона фермер
- 12. Матрица сожалений для примераСоставим матрицу сожалений. Находим максимум по каждому столбцуМатрица сожалений имеет вид
- 13. Критерий ЛапласаПри заданных вероятностях P{sj} = 1/4,
- 14. Критерий ВальдаМинимальные элементы строк матрицы последствий
- 15. Критерий СэвиджаМаксимальные элементы строк матрицы сожалений R
- 16. Критерий ГурвицаПри α = 0,5 и α
- 17. Критерии ожидаемого значенияПредположим, что в рассмотренной схеме
- 18. Правило максимизации доходаДоход, получаемый при принятии i-го
- 19. Правило минимизации ожидаемых сожаленийСожаления при реализации i-го
- 20. Теорема эквивалентности правил максимизации ожидаемого дохода и
- 21. Пример 2Компания «Российский сыр» – небольшой производитель
- 22. Решение примера 2Пользуясь исходными данными, строим матрицу
- 23. Решение примера 2. Платежная матрицаНа практике чаще
- 24. Решение примера 2. Вычисление дисперсии6 ящиков 7 ящиков8 ящиков9 ящиков
- 25. Выводы к примеру 2Из представленных результатов расчетов
- 26. Дерево решенийПозиционные игры
- 27. Дерево решенийДерево решений – это графическое средство
- 28. Этапы построения дерева решенийПостановка проблемы и поиск
- 29. Этапы процесса принятия решений с помощью дерева
- 30. Пример 3Руководство некоторой компании решает, создавать ли
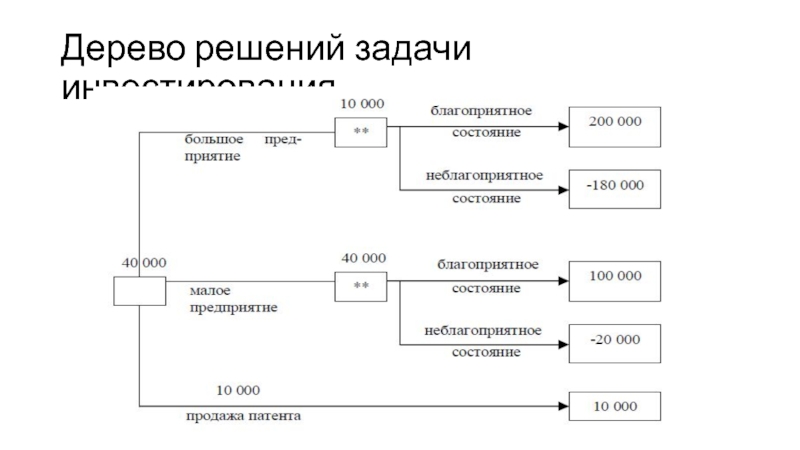
- 31. Дерево решений задачи инвестирования
- 32. Правило максимизации доходаВычислим средний ожидаемый доход инвестора
- 33. Ожидаемая ценность точной информацииПредположим, что консультационная фирма
- 34. Пример расчета ожидаемой ценности точной информации Рассчитаем
- 35. Ожидаемая ценность точной информацииТогда ожидаемая ценность точной
- 36. Усложненная задача строительстваПусть перед тем, как принимать
- 37. Усложненная задача строительстваОтносительно фирмы, которой можно заказать
- 38. Дерево решений
- 39. Результаты исследованияАнализируя дерево решений, можно сделать следующие
- 40. Апостериорные вероятности
- 41. Апостериорные вероятности БайесаВ некоторых случаях оказывается возможным
- 42. Пример 4. Задача инвестирования Предположим, что вы
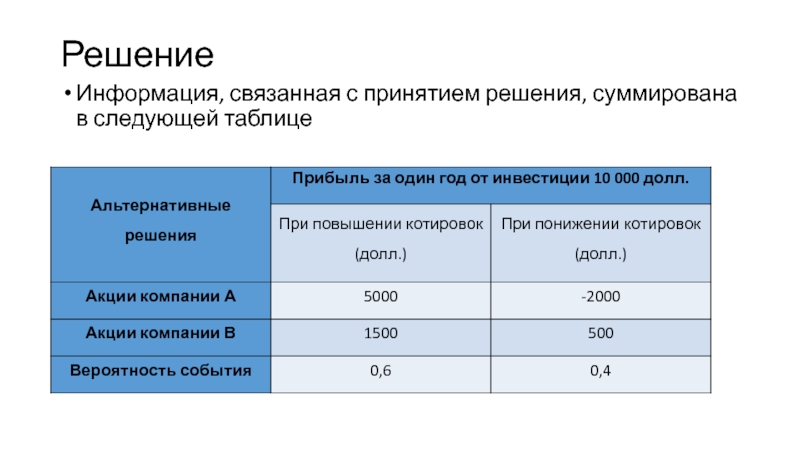
- 43. Решение Информация, связанная с принятием решения, суммирована в следующей таблице
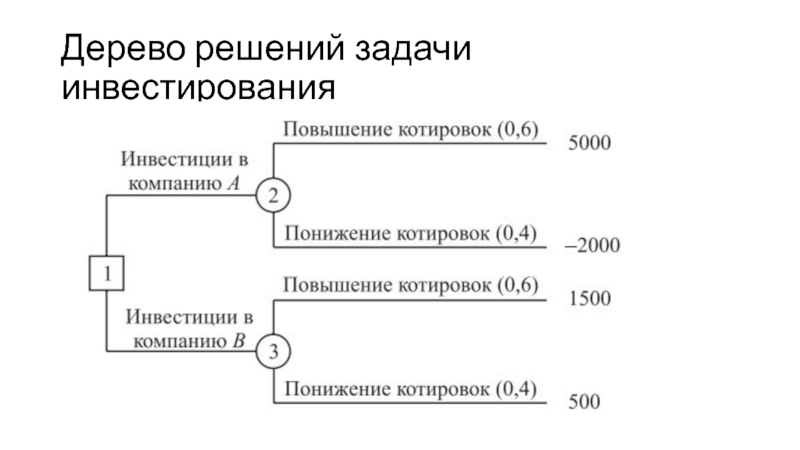
- 44. Дерево решений задачи инвестирования
- 45. Правило максимизации доходаОжидаемая прибыль за год для
- 46. Пример 5 В примере 4 априорные вероятности
- 47. Решение Введем следующие обозначения: v1 – мнение «за», v2
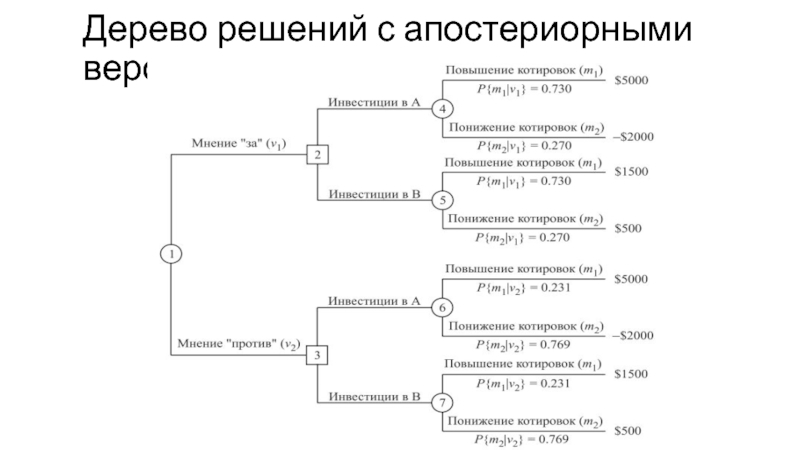
- 48. Дерево решений с апостериорными вероятностями
- 49. Решение Вычислим апостериорные вероятности Р{mi | vj},
- 50. Решение Шаг 2. Вычисляем вероятности совместного появления
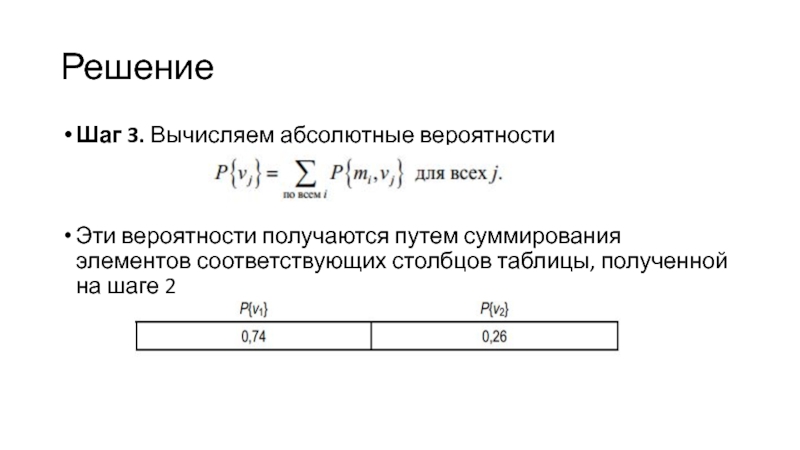
- 51. Решение Шаг 3. Вычисляем абсолютные вероятностиЭти вероятности
- 52. Решение Шаг 4. Определяем искомые апостериорные вероятности
- 53. Решение Оценим альтернативные решения, основанные на ожидаемых
- 54. Примеры
- 55. Пример 1 Исследовать ситуацию принятия решений в
- 56. Решение Составим матрицу сожалений. Имеем:Поэтому матрица сожалений
- 57. Правило ВальдаПо правилу Вальда (правилу крайнего пессимизма)
- 58. Правило СэвиджаПравило Сэвиджа аналогично правилу Вальда, только
- 59. Критерии ожидаемого значенияПравило максимизации ожидаемого дохода рекомендует
- 60. Пример 2 Сидя в отправляющемся на курорт
- 61. Решение У Пети есть две стратегии: поехать
- 62. Матрица сожалений для примераСоставим матрицу сожалений. Максимум
- 63. Критерий ЛапласаПри заданных вероятностях P{sj} = 1/2,
- 64. Критерий ВальдаМинимальные элементы строк матрицы последствий
- 65. Критерий СэвиджаМаксимальные элементы строк матрицы сожалений
- 66. Критерий ГурвицаПри λ = 0,5 оптимальным решением
- 67. Скачать презентанцию
Понятие игры с природойМатричная игра, где игрок взаимодействует с окружающей средой, которая не заинтересована в его проигрыше, и решает задачу определения оптимальной стратегии с учетом неопределенности состояния окружающей среды, называется игрой
Слайды и текст этой презентации
Слайд 3Неопределенность
Лицу, принимающему решение известен лишь набор возможных вариантов состояний
внешней среды
В условиях неопределенности вероятностное распределение, соответствующее состояниям j (
j = 1, 2, ..., n) либо неизвестно, либо не может быть определеноСитуация с полной неопределенностью характеризуется отсутствием какой бы то ни было дополнительной информации
Слайд 4Матрица последствий
Если будет принято i-e решение, а состояние внешней среды
соответствует j-й ситуации, то лицо, принимающее решение, получит доход qij.
Плата (или доход), связанная с решением Аi и состоянием внешней среды sj, равна qij
Матрица Q=(qij), i=1,2,…,m, j=1,2,…,n называется матрицей последствий (платежной матрицей)
Слайд 5Матрица сожалений (рисков)
Допустим, мы хотим оценить риск, который несет i-e
решение. Нам неизвестна реальная ситуация. Но если бы мы знали,
что осуществляется j-е состояние внешней среды, то выбрали бы наилучшее решение, т. е. приносящее наибольший доходqj = max(qkj), k=1,2,…,m
Значит, принимая i-e решение, мы рискуем получить не qj, а только qij, т. е. если мы примем i-е решение, а во внешней среде реализуется j-е состояние, то мы будем сожалеть о недополученном доходе в размере
rij = qj – qij = max(qkj) – qij , k=1,2,…,m
Матрица R= (rij ) называется матрицей сожалений (матрицей рисков)
Слайд 7Максимаксный критерий (критерий крайнего оптимизма)
Максимаксный (минимаксный) критерий основан на оптимистичном
поведении лица, принимающего решение, и сводится к выбору наилучшей альтернативы
из наилучших. Если величина qij представляет получаемую прибыль, то в соответствии с максимаксным критерием в качестве оптимального выбирается решение, обеспечивающееmaxi { maxj (qij ) }
Если величина qij представляет потери, используется минимаксный критерий, который определяется следующим соотношением
mini { maxj (qij ) }
Слайд 8Правило Вальда (крайнего пессимизма)
Рассматривая i-e решение, будем полагать, что
на самом деле складывается ситуация, наихудшая с нашей точки зрения
(т. е. приносящая наименьший доход ) и выберем решение i0 с наибольшим ai .Необходимо принять такое решение i0 , что
Слайд 9Правило Сэвиджа
Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем
замены матрицы платежей (выигрышей или проигрышей) qij матрицей потерь rij
. При применении этого правила анализируется матрица сожалений R. Рассматривая i-e решение, будем полагать, что на самом деле складывается ситуация максимальных сожаленийи выберем решение i0 с наименьшим bi .
Необходимо принять такое решение i0 , что
Слайд 10Правило Гурвица
При любом выборе стратегии наихудший для игрока А вариант
реализуется с вероятностью α, а наилучший с вероятностью 1 –
α,α –показатель пессимизма (0 ≤ α ≤1).
Если aij – выигрыш (полезность) игрока, то оптимальной стратегией считается та, для которой достигается значение G:
Если aij – потери игрока (затраты), то
Значение α выбирается из субъективных соображений.
Если α →1, то правило Гурвица приближается к правилу Вальда, если α →0, то правило Гурвица приближается к правилу розового оптимизма
Слайд 11Пример 1
В приближении посевного сезона фермер Мак-Кой имеет 4
альтернативы: выращивать кукурузу (a1), пшеницу (a2), соевые бобы (a3) или
использовать землю под пастбища (a4). Платежи, связанные с указанными возможностями, зависят от количества осадков, которые условно можно разделить на 4 категории: сильные осадки (s1), умеренные осадки (s2), незначительные осадки (s3), засушливый сезон (s4). Платежная матрица (в тыс. долларов) оценивается следующим образом.Что должен посеять фермер Мак-Кой?
Слайд 12Матрица сожалений для примера
Составим матрицу сожалений. Находим максимум по каждому
столбцу
Матрица сожалений имеет вид
Слайд 13Критерий Лапласа
При заданных вероятностях P{sj} = 1/4, j = 1,
2, 3, 4 ожидаемые значения платежей для различных возможных решений
вычисляются следующим образом.M{a1} = (1/4)(-20 + 60 + 30 - 5) = 16,25,
M{a2} = (1/4)(40 + 50 + 35 + 0) = 31,25,
M{a3} = (1/4)(-50 + 100 + 45 - 10) = 21,25,
M{a4} = (1/4)(12 + 15 + 15 + 10) = 13,
Наибольшее значение платежей соответствует второй стратегии a2 , т.е. правило Лапласа рекомендует посеять пшеницу.
Слайд 14Критерий Вальда
Минимальные элементы строк матрицы последствий
a1 =min(-20, 60,
30, -5) = -20,
a2 =min(40, 50, 35, 0)
= 0, a3 =min(-50, 100, 45, -10) = -50,
a4 =min(12, 15, 15, 10) = 10,
Теперь находим оптимальное решение
ai0 = max(-20, 0, -50, 10) = 10.
Значит, правило Вальда рекомендует принять четвертое решение, т.е. использовать земли под пастбища.
Слайд 15Критерий Сэвиджа
Максимальные элементы строк матрицы сожалений R
b1 = max(60,
40, 15, 15) = 60,
b2 = max(0, 50, 10, 10)
= 50, b3 = max(90, 0, 0, 20) = 90,
b4 = max(28, 85, 30, 0) = 85,
Теперь находим оптимальное решение
bi0 = min(60, 50, 90, 85) = 50.
Значит, правило Сэвиджа также, как и правило Вальда, рекомендует принять второе решение, т.е. посеять пшеницу
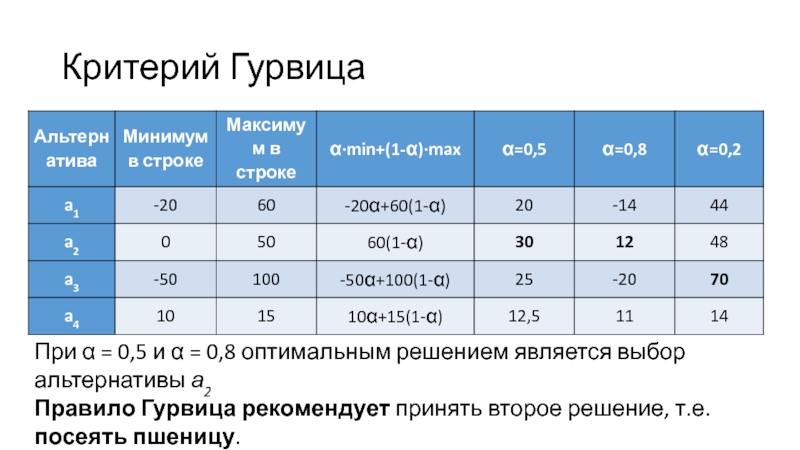
Слайд 16Критерий Гурвица
При α = 0,5 и α = 0,8 оптимальным
решением является выбор альтернативы а2
Правило Гурвица рекомендует принять второе
решение, т.е. посеять пшеницу.Слайд 17Критерии ожидаемого значения
Предположим, что в рассмотренной схеме известны вероятности pj
того, что реальная ситуация развивается по варианту j. Именно такое
положение называется частичной неопределенностью (риском).При принятии решений в таких ситуациях можно выбрать одно из следующих правил:
Правило максимизации дохода
Правило минимизации ожидаемых сожалений
Слайд 18Правило максимизации дохода
Доход, получаемый при принятии i-го решения, является случайной
величиной Qi с рядом распределения
Ожидаемый доход при принятии i-го решения
оценивается математическим ожиданием MQi соответствующей случайной величины Qi. Правило максимизации ожидаемого дохода рекомендует принять решение, приносящее максимальный ожидаемый доход.
Слайд 19Правило минимизации ожидаемых сожалений
Сожаления при реализации i-го решения представляются случайной
величиной Ri с рядом распределения
Ожидаемые сожаления оценивается математическим ожиданием MRi
соответствующей случайной величины Ri. Правило минимизации ожидаемых сожалений рекомендует принять решение, влекущее минимальные ожидаемые сожаления
Слайд 20Теорема эквивалентности правил максимизации ожидаемого дохода и минимизации ожидаемых сожалений
Решения,
рекомендуемые правилами максимизации ожидаемого дохода и минимизации ожидаемых сожалений, всегда
совпадают.Слайд 21Пример 2
Компания «Российский сыр» – небольшой производитель различных продуктов из
сыра на экспорт. Один из продуктов – сырная паста –
поставляется в страны ближнего зарубежья. Генеральный директор должен решить, сколько ящиков сырной пасты следует производить в течение месяца. Вероятности того, что спрос на сырную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равны соответственно 0,1; 0,3; 0,5; 0,1.Затраты на производство одного ящика равны 45 дол. Компания продает каждый ящик по цене 95 дол. Если ящик с сырной пастой не продается в течение месяца, то она портится и компания не получает дохода. Сколько ящиков следует производить в течение месяца?
Слайд 22Решение примера 2
Пользуясь исходными данными, строим матрицу игры
Стратегиями игрока 1
(компания «Российский сыр») являются различные показатели числа ящиков с сырной
пастой, которые ему, возможно, следует производитьСостояниями природы выступают величины спроса на аналогичное число ящиков
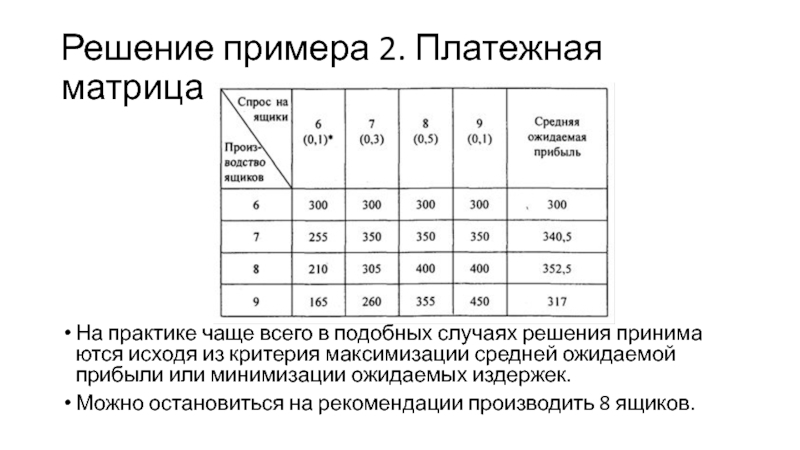
Слайд 23Решение примера 2. Платежная матрица
На практике чаще всего в подобных
случаях решения принимаются исходя из критерия максимизации средней ожидаемой прибыли
или минимизации ожидаемых издержек.Можно остановиться на рекомендации производить 8 ящиков.
Слайд 25Выводы к примеру 2
Из представленных результатов расчетов с учетом полученных
показателей рисков – средних квадратичных отклонении – очевидно, что производить
9 ящиков при любых обстоятельствах нецелесообразно, ибо средняя ожидаемая прибыль, равная 317, меньше, чем для 8 ящиков (352,5), а среднее квадратичное отклонение (76) для 9 ящиков больше аналогичного показателя для 8 ящиков (63,73).А вот целесообразно ли производство 8 ящиков по сравнению с 7 или 6 - неочевидно, так как риск при производстве 8 ящиков ( = 63,73) больше, чем при производстве 7 ящиков ( = 28,5) и тем более 6 ящиков, где = 0.
Вся информация с учетом ожидаемых прибылей и рисков налицо. Решение должен принимать генеральный директор компании «Российский сыр» с учетом его опыта, склонности к риску и степени достоверности показателей вероятностей спроса: 0,1; 0,3; 0,5; 0,1.
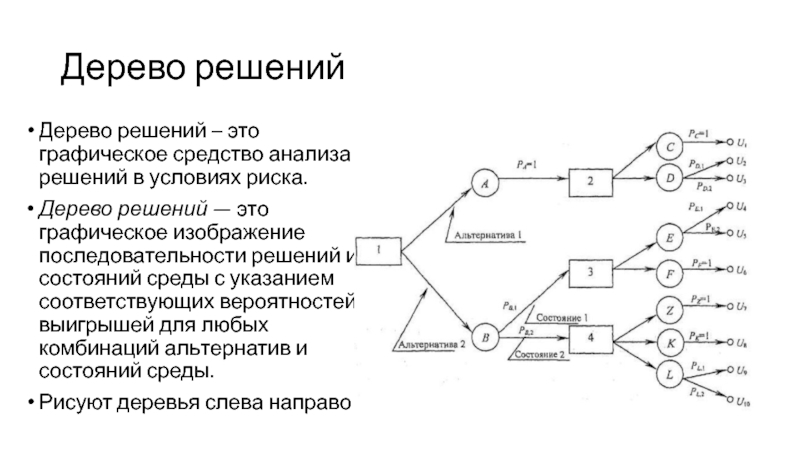
Слайд 27Дерево решений
Дерево решений – это графическое средство анализа решений в
условиях риска.
Дерево решений — это графическое изображение последовательности решений и
состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.Рисуют деревья слева направо
Слайд 28Этапы построения дерева решений
Постановка проблемы и поиск альтернатив решения
Конструирование дерева
решений в виде схематичного представления комплекса решаемых подпроблем
Анализ дерева решений
производится, начиная от конечных исходов к начальному узлу принятия решений. Такой процесс вычислений называется обратным пересчетомАнализ устойчивости решения
Оценка ожидаемой ценности точной информации
Слайд 29Этапы процесса принятия решений с помощью дерева решений
Этап 1. Формулирование
задачи (необходимо отбросить не относящиеся к проблеме факторы, а среди
множества оставшихся выделить существенные и несущественные).Основные процедуры:
определение возможностей сбора информаций для экспериментирования и реальных действии;
составление перечня событии, которые с определенной вероятностью могут произойти;
установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять
Этап 2. Построение дерева решений
Этап 3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события
Этап 4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды.
Этап 5. Решение задачи
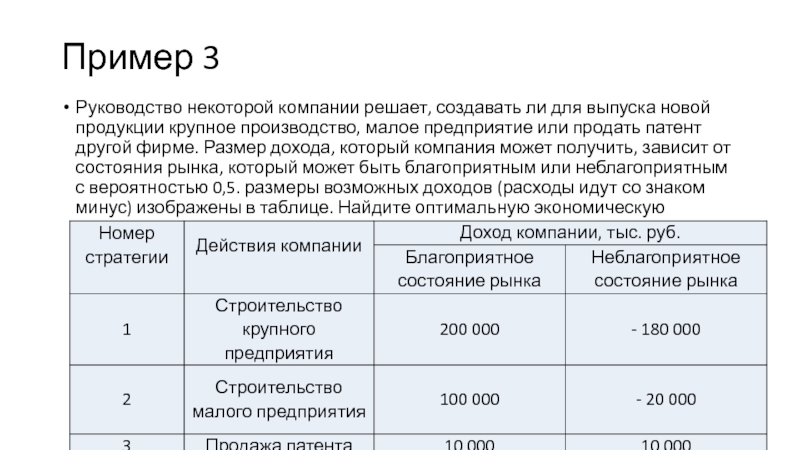
Слайд 30Пример 3
Руководство некоторой компании решает, создавать ли для выпуска новой
продукции крупное производство, малое предприятие или продать патент другой фирме.
Размер дохода, который компания может получить, зависит от состояния рынка, который может быть благоприятным или неблагоприятным с вероятностью 0,5. размеры возможных доходов (расходы идут со знаком минус) изображены в таблице. Найдите оптимальную экономическую стратегию предприятияСлайд 32Правило максимизации дохода
Вычислим средний ожидаемый доход инвестора при каждой возможной
стратегии
MQ1 = 0,5 × 200 000 + 0,5 ×(-180 000)
= 10 000 тыс. руб.;MQ2 = 0,5 × 100 000 + 0,5 ×(-20 000) = 40 000 тыс. руб.;
MQ3 = 10 000 тыс. руб.
Наиболее целесообразно выбрать стратегию а2, т.е. строить малое предприятие, а ветви (стратегии) а1 и а3 дерева решений можно отбросить
Ожидаемая денежная оценка наилучшего решения равна 40 000 тыс.руб.
Слайд 33Ожидаемая ценность точной информации
Предположим, что консультационная фирма за определенную плату
готова предоставить информацию о фактической ситуации на рынке в тот
момент, когда руководству компании надлежит принять решение о масштабе производстваОжидаемая ценность точной информации о фактическом состоянии рынка равна разности между ожидаемой денежной оценкой при наличии точной информации и максимальной ожидаемой денежной оценкой при отсутствии точной информации
Слайд 34Пример расчета ожидаемой ценности точной информации
Рассчитаем ожидаемую ценность точной
информации для примера, в котором дополнительное обследование конъюнктуры рынка не
проводится.При отсутствии точной информации максимальная ожидаемая денежная оценка равна:
ОДО = 0,5 × 100 000 - 0,5 × 20 000 = 40 000 тыс. руб.
Если точная информация об истинном состоянии рынка будет благоприятной, то
ОДОт.и = 0,5 × 200 000 + 0,5 × 10 000 = 105 000 тыс. руб.
Слайд 35Ожидаемая ценность точной информации
Тогда ожидаемая ценность точной информации равна:
ОЦт.и =
ОДОт.и - ОДО = 105 000 - 40 000 =
65 000 тыс. руб.Значение ОЦт.и показывает, какую максимальную цену должна быть готова заплатить компания за точную информацию об истинном состоянии рынка в тот момент, когда ей это необходимо
Слайд 36Усложненная задача строительства
Пусть перед тем, как принимать решение о строительстве,
руководство компании должно определить, заказывать ли дополнительное исследование состояния рынка
или нет, причем предоставляемая услуга обойдется компании в 10 000 дол. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностейСлайд 37Усложненная задача строительства
Относительно фирмы, которой можно заказать прогноз, известно, что
она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Например,
когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятном рынке оправдывается с вероятностью 0,73. Фирма утверждает, что ситуация будет благоприятной с вероятностью 0,45 и неблагоприятной с вероятностью 0,55.Следует ли заказывать фирме дополнительное обследование рынка?
Какую максимальную сумму фирма может выплатить консультационной фирме за проделанную работу?
Какова ожидаемая денежная оценка наилучшего решения?
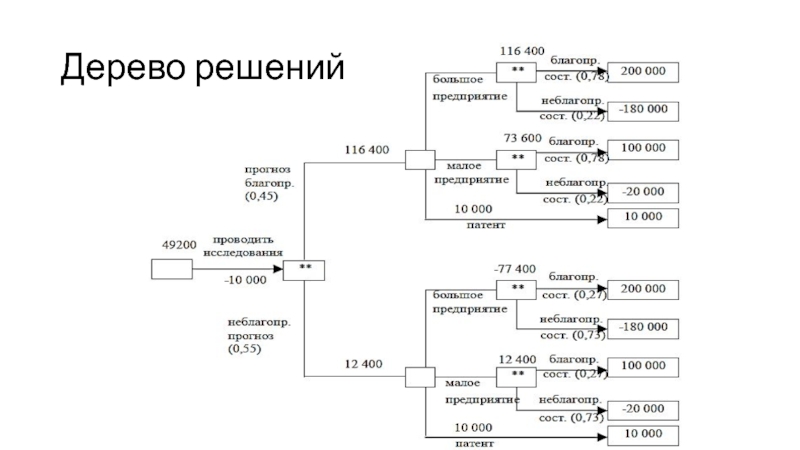
Слайд 39Результаты исследования
Анализируя дерево решений, можно сделать следующие выводы:
необходимо проводить дополнительное
исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение;
если
фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно строить большое предприятие (ожидаемая максимальная прибыль 116 400 тыс. руб.), если прогноз неблагоприятный – малое (ожидаемая максимальная прибыль 12 400 тыс. руб.).максимальная сумма, которую компания может заплатить за услуги фирмы составляет 59 200 - 40 000 = 19 200 тыс. руб.
Слайд 41Апостериорные вероятности Байеса
В некоторых случаях оказывается возможным пересчитать вероятности, которые
используются при формулировке критерия ожидаемого значения, с помощью текущей и/или
полученной ранее информации, которая обычно основывается на исследовании выборочных (или экспериментальных) данных. Получаемые при этом вероятности называют апостериорными (или байесовскими), в отличие от априорных, полученных из исходной информацииСлайд 42Пример 4. Задача инвестирования
Предположим, что вы хотите вложить на
фондовой бирже 10 000 долл. в акции одной из двух
компаний: А или В. Акции компании А являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20%. Компания В обеспечивает безопасность инвестиций с 15% прибыли в условиях повышения котировок на бирже и только 5% в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60 % прогнозируют повышение котировок и с вероятностью 40 % – понижение котировок. В какую компанию следует вложить деньги?Слайд 45Правило максимизации дохода
Ожидаемая прибыль за год для каждой из двух
альтернатив.
Для акций компании А:
MQ1 = 5000 × 0,6 +
(-2000) × 0,4 = 2 200 (долл.).Для акций компании B:
MQ2 = 1500 × 0,6 + 500 × 0,4 = 1 100 (долл.).
Решением, основанным на этих вычислениях, является покупка акций компании А.
Слайд 46Пример 5
В примере 4 априорные вероятности 0,6 и 0,4
повышения и понижения котировок акций на бирже были определены из
наличных публикаций финансового характера.Предположим, вместо того, чтобы полностью полагаться на эти публикации, вы решили провести личное исследование путем консультаций с другом, который хорошо разбирается в вопросах, касающихся фондовой биржи. Друг высказывает общее мнение «за» или «против» инвестиций. Это мнение в дальнейшем определяется количественно следующим образом. При повышении котировок его мнение с 90% - ной вероятностью будет «за», при снижении котировок вероятность его мнения «за» уменьшится до 50%. Каким образом можно извлечь пользу из этой дополнительной информации?
Слайд 47Решение
Введем следующие обозначения:
v1 – мнение «за»,
v2 – мнение «против»,
m1
– повышение котировок,
m2 – понижение котировок.
Мнение друга можно записать в
виде вероятностных соотношений следующим образом.Р{v1 | m1} = 0,9,
Р{v1 | m2} = 0,1,
Р{v2 | m1} = 0,5,
Р{v2 | m2} = 0,5.
Слайд 49Решение
Вычислим апостериорные вероятности Р{mi | vj}, указанные на соответствующих
ветвях, выходящих из узлов 4 – 7.
Шаг 1. Условные вероятности
Р{vj| mi} для данной задачи запишем следующим образомСлайд 50Решение
Шаг 2. Вычисляем вероятности совместного появления событий
При заданных
априорных вероятностях Р{m1}=0,6 и Р{m2}=0,4 вероятности совместного появления событий определяются
умножением первой и второй строк таблицы, полученной на шаге 1, на 0,6 и 0,4 соответственноСлайд 51Решение
Шаг 3. Вычисляем абсолютные вероятности
Эти вероятности получаются путем суммирования
элементов соответствующих столбцов таблицы, полученной на шаге 2
Слайд 52Решение
Шаг 4. Определяем искомые апостериорные вероятности по формуле
Эти вероятности
вычисляются в результате деления каждого столбца таблицы, полученной на шаге
2, на элемент соответствующего столбца таблицы, вычисленной на шаге 3, что приводит к следующим результатам (округленным до трех десятичных знаков).Слайд 53Решение
Оценим альтернативные решения, основанные на ожидаемых платежах для узлов
4 – 7.
Мнение «за»
Доход от акций компании А в узле
4 = 5000 × 0,730 + (-2000) × 0,270 = 3110 (долл.).Доход от акций компании B в узле 5 = 1500 × 0,730 + 500 × 0,270 = 1230 (долл.).
Решение. Инвестировать в акции компании А.
Мнение «против»
Доход от акций компании А в узле 6 = 5000 × 0,231 + (-2000) × 0,769 = -383 (долл.).
Доход от акций компании B в узле 7 = 1500 × 0,231 + 500 × 0,769 = 731 (долл.).
Решение. Инвестировать в акции компании B.
Слайд 55Пример 1
Исследовать ситуацию принятия решений в условиях неопределенности в
случае, когда матрица последствий
Найти оптимальное решение, если известны вероятности состояний
внешней среды1/2, 1/6, 1/6, 1/6.
Слайд 57Правило Вальда
По правилу Вальда (правилу крайнего пессимизма) будем полагать, что
при принятии i -го решения на самом деле складывается самая
плохая ситуация, т. е. приносящая наименьший доход , и выберем решение i0 с наибольшим ai0.Имеем:
Из этих чисел 2, 2, 3, 1 находим максимальное: это 3.
Значит, правило Вальда рекомендует принять третье решение.
Слайд 58Правило Сэвиджа
Правило Сэвиджа аналогично правилу Вальда, только анализируется матрица сожалений:
рассматривая i -e решение, будем полагать, что на самом деле
складывается ситуация максимальных сожалений , и выберем решение i0 с наименьшим bi0 .Имеем
Из этих чисел 8, 6, 5, 7 находим минимальное. Это 5.
Значит, правило Сэвиджа рекомендует принять третье решение.
Слайд 59Критерии ожидаемого значения
Правило максимизации ожидаемого дохода рекомендует принять решение, соответствующее
наибольшему из ожидаемых доходов:
MQ1 = 23/6, MQ2= 25/6, MQ3= 7
MQ4= 17/6.Максимальный ожидаемый доход равен 7, что соответствует третьему решению.
Правило минимизации ожидаемых сожалений рекомендует принять решение, соответствующее наименьшему из ожидаемых сожалений:
MR1 = 20/6, MR2= 4, MR3= 7/6, MR4= 32/5,
т. е. опять третье решение.
Слайд 60Пример 2
Сидя в отправляющемся на курорт поезде, перед самым
отправлением Петя вдруг вспомнил, что, кажется, забыл выключить дома утюг.
Можно еще успеть сойти с поезда и исправить ошибку, но тогда пропадет путевка (100 000 руб.). Если же уехать, утюг, если он действительно включен, может стать причиной пожара, и тогда придется ремонтировать квартиру (1 500 000 руб.). Петя не уверен, включен утюг или выключен. Составить матрицу последствий и матрицу сожалений. Определить решения, рекомендуемые критериями Лапласа, Вальда, Сэвиджа, Гурвица.Слайд 61Решение
У Пети есть две стратегии: поехать отдыхать или вернуться
домой. У внешней среды также есть два состояния: утюг выключен
либо утюг включен.Матрица последствий имеет вид
Слайд 62Матрица сожалений для примера
Составим матрицу сожалений. Максимум по первому столбцу
равен
по второму –
Матрица сожалений имеет вид
Слайд 63Критерий Лапласа
При заданных вероятностях P{sj} = 1/2, j = 1,
2, ожидаемые значения платежей для различных возможных решений вычисляются следующим
образом.M{a1} = (1/2)(0 + (-1 500 000 )) = - 750 000,
M{a2} = (1/2)(-100 000 + (-100 000)) = -100 000.
Наибольшее значение платежей соответствует второй стратегии a2 , т.е. правило Лапласа рекомендует вернуться домой.
Слайд 64Критерий Вальда
Минимальные элементы строк матрицы последствий
a1 =min(0, -1
500 000) = -1 500 000,
a2 =min(-100 000,
-100 000) = -100 000. Теперь находим оптимальное решение
ai0 = max(-1 500 000, -100 000) = -100 000.
Значит, правило Вальда рекомендует принять второе решение, т.е. вернуться домой.
Слайд 65Критерий Сэвиджа
Максимальные элементы строк матрицы сожалений
b1 = max(0,
1 400 000) = 1 400 000,
b2 = max(0,
100 000) = 100 000. Теперь находим оптимальное решение
bi0 = min(1 400 000, 100 000) = 100 000.
Значит, правило Сэвиджа также, как и правило Вальда, рекомендует принять второе решение, т.е. вернуться домой
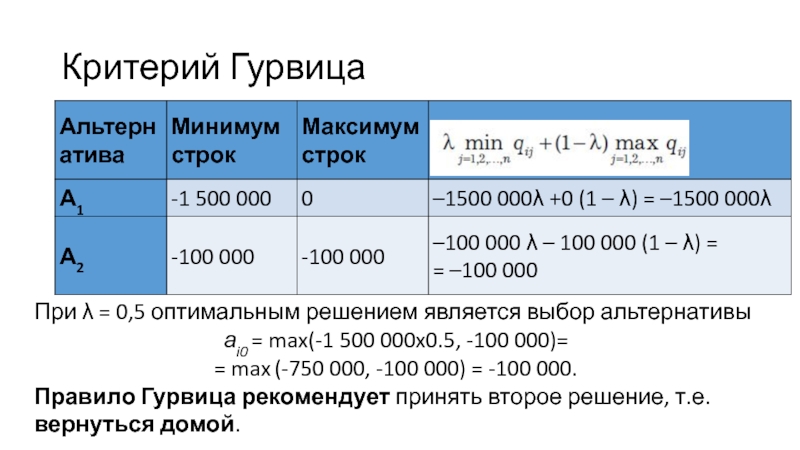
Слайд 66Критерий Гурвица
При λ = 0,5 оптимальным решением является выбор альтернативы
аi0 = max(-1 500 000x0.5, -100 000)=
= max (-750 000,
-100 000) = -100 000. Правило Гурвица рекомендует принять второе решение, т.е. вернуться домой.