Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИНЖЕНЕРНАЯ ГРАФИКА установочная лекция для студентов очного
Содержание
- 1. ИНЖЕНЕРНАЯ ГРАФИКА установочная лекция для студентов очного
- 2. Слайд 2
- 3. ОБЩИЕ ПОЛОЖЕНИЯ ЕДИНОЙ СИСТЕМЫ КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ ГОСТ 2.001
- 4. 2. ОБЛАСТЬ РАСПРОСТРАНЕНИЯ СТАНДАРТОВ ЕСКД Установленные стандартами ЕСКД
- 5. Состав стандартов, входящих в ЕСКД, определяется перечнем,
- 6. Номер стандарта составляется из: цифры 2, присвоенной
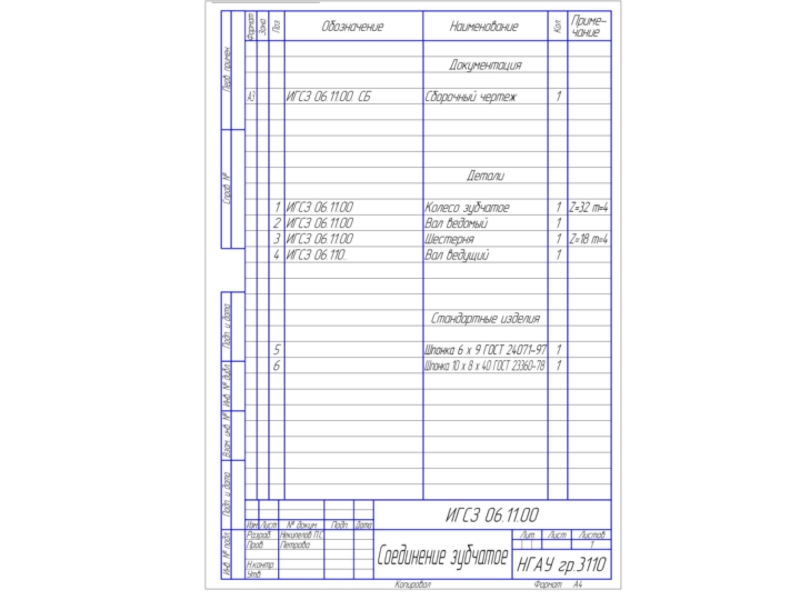
- 7. Согласно ГОСТ 2.104 - 68 в констpуктоpских
- 8. При выполнении чертежей пользуются форматами, установленными ГОСТ
- 9. 1. Сплошная толстая основная линия применяется для
- 10. Основным паpаметpом шрифта является его pазмеp h
- 11. Слайд 11
- 12. Деление угла пополам (построение биссектрисы)2. Из точки
- 13. Деление прямого угла на 3 равные части3.
- 14. Деление окружности на равные частиДеление окружности на четыре
- 15. Деление окружности на три и шесть частей 1.
- 16. Деление окружности на пять равных частей1. Провести
- 17. Сопряжением называется плавный переход одной линии в
- 18. 1. Из вершины О проводят дугу произвольным
- 19. OO1rR+rRrnn1Внешнее сопряжение прямой линии с дугой3. Соединяем
- 20. R2nOO1O2R1R1+R2n1R+R2RLL12. Соединяем прямыми центр сопряжения О2 с
- 21. Лекальными кривыми называются плоские кривые, вычерчиваемые при помощи лекал по предварительно найденным точкамПараболаСинусоидаЭвольвентаЦиклоидаЭллипсПарабола
- 22. Эллипс - замкнутая плоская выпуклая кривая, сумма
- 23. Парабола - плоская кривая каждая точка которой
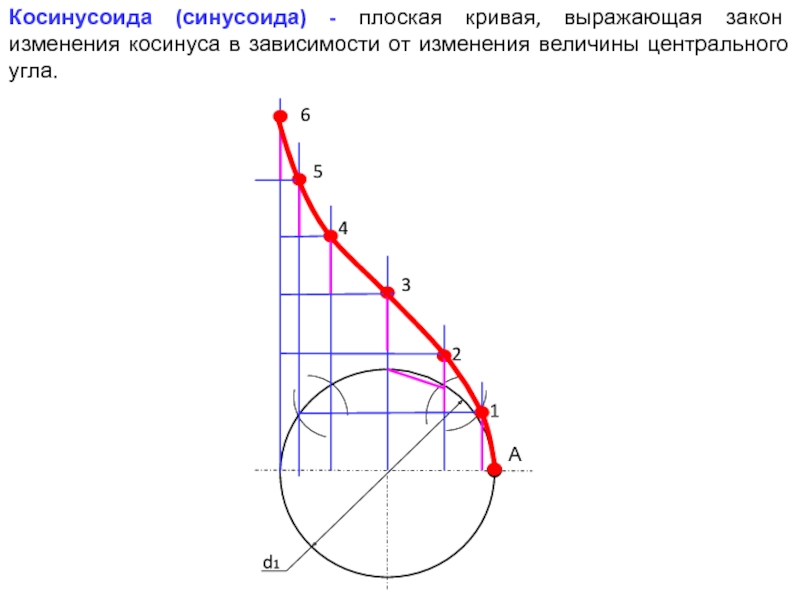
- 24. Косинусоида (синусоида) - плоская кривая, выражающая закон
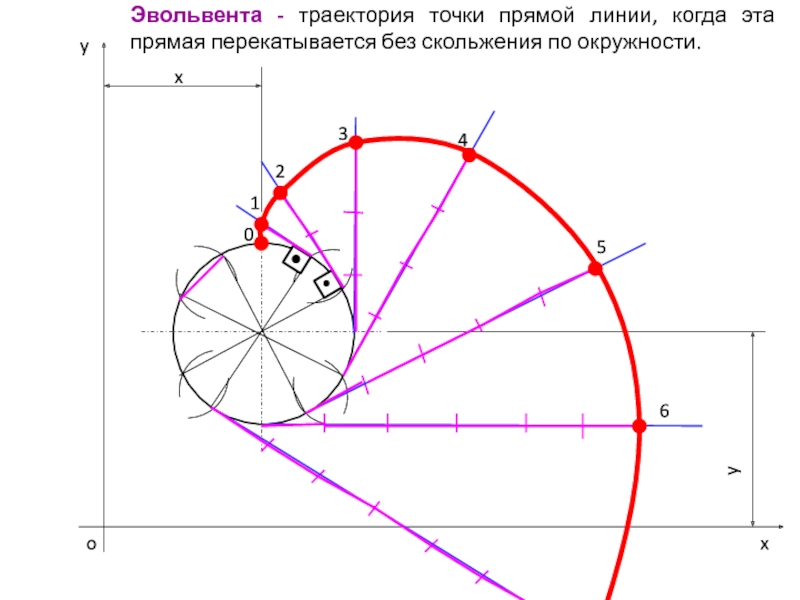
- 25. Эвольвента - траектория точки прямой линии, когда эта прямая перекатывается без скольжения по окружности. oxyxy01234567
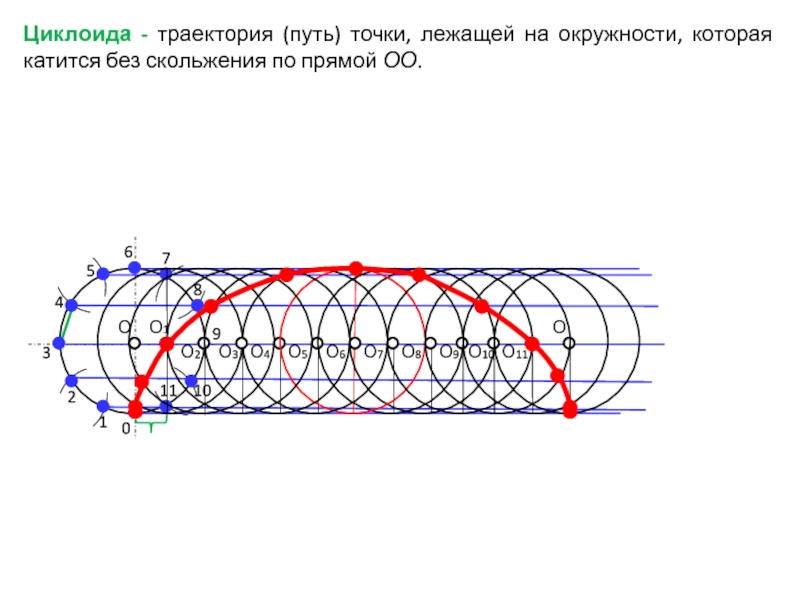
- 26. Циклоида - траектория (путь) точки, лежащей на
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ИНЖЕНЕРНАЯ ГРАФИКА
установочная лекция
для студентов очного отделения
Инженерного института НГАУ
Составитель Семенова
Т.В.
Слайд 3ОБЩИЕ ПОЛОЖЕНИЯ
ЕДИНОЙ СИСТЕМЫ КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ
ГОСТ 2.001 - 70 устанавливает общие
положения по целевому назначению, области распространения, классификации и обозначению стандартов,
входящих в комплекс Единой системы конструкторской документации (ЕСКД).1. ОПРЕДЕЛЕНИЕ И НАЗНАЧЕНИЕ
Единая система конструкторской документации - комплекс государственных стандартов, устанавливающих взаимосвязанные правила и положения по порядку разработки, оформления и обращения конструкторской документации, разрабатываемой и применяемой организациями и предприятиями.
Основное назначение стандартов ЕСКД - установление в организациях и на предприятиях единых правил выполнения, оформления и обращения конструкторской документации, которые должны обеспечивать:
возможность взаимообмена конструкторскими документами между организациями и предприятиями без их переоформления;
стабилизацию комплектности, исключающую дублирование и разработку не требуемых производству документов;
возможность расширения унификации при конструкторской разработке проектов промышленных изделий;
упрощение форм конструкторских документов графических изображений, снижающее трудоемкость проектно-конструкторских разработок промышленных изделий;
механизацию и автоматизацию обработки технических документов и содержащейся в них информации;
улучшение условий технической подготовки производства;
улучшение условий эксплуатации промышленных изделий;
оперативную подготовку документации для быстрой переналадки действующего производства.
Слайд 42. ОБЛАСТЬ РАСПРОСТРАНЕНИЯ СТАНДАРТОВ ЕСКД
Установленные стандартами ЕСКД правила и положения
по разработке, оформлению и обращению документации распространяются:
на все виды
конструкторских документов; на учетно-регистрационную документацию и документацию по внесению изменений в конструкторские документы;
на нормативно-техническую и технологическую документацию, а также научно-техническую и учебную литературу в той части, в которой они могут быть для них применены и не регламентируются специальными стандартами и нормативами, устанавливающими правила выполнения этой документации и литературы, например форматов и шрифтов для печатных изданий и т. п.
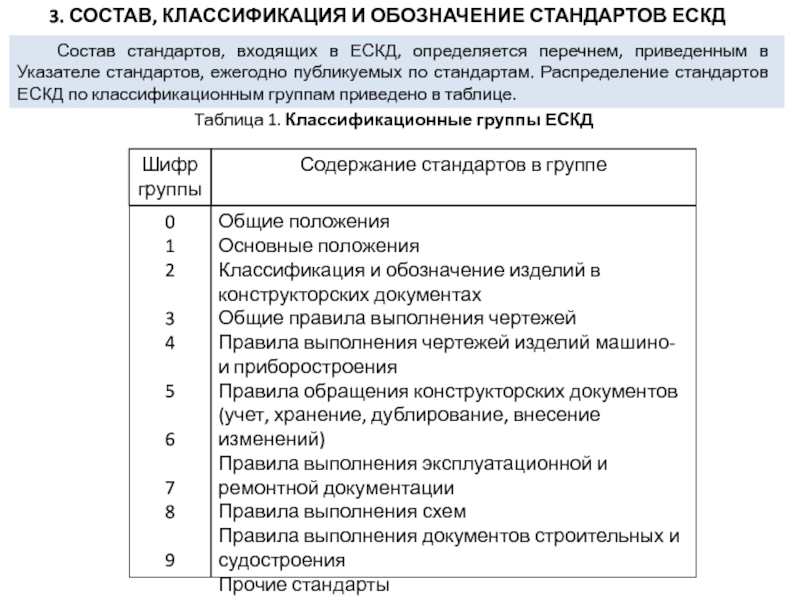
Слайд 5 Состав стандартов, входящих в ЕСКД, определяется перечнем, приведенным в Указателе
стандартов, ежегодно публикуемых по стандартам. Распределение стандартов ЕСКД по классификационным
группам приведено в таблице.Таблица 1. Классификационные группы ЕСКД
0
1
2
3
4
5
6
7
8
9
Общие положения
Основные положения
Классификация и обозначение изделий в конструкторских документах
Общие правила выполнения чертежей
Правила выполнения чертежей изделий машино- и приборостроения
Правила обращения конструкторских документов (учет, хранение, дублирование, внесение изменений)
Правила выполнения эксплуатационной и ремонтной документации
Правила выполнения схем
Правила выполнения документов строительных и судостроения
Прочие стандарты
Шифр
группы
Содержание стандартов в группе
3. СОСТАВ, КЛАССИФИКАЦИЯ И ОБОЗНАЧЕНИЕ СТАНДАРТОВ ЕСКД
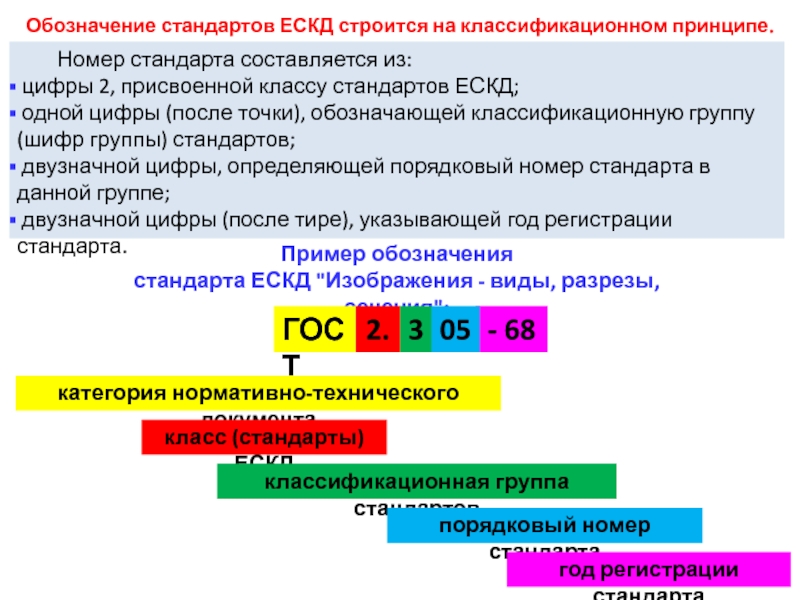
Слайд 6 Номер стандарта составляется из:
цифры 2, присвоенной классу стандартов ЕСКД;
одной цифры (после точки), обозначающей классификационную группу (шифр группы)
стандартов; двузначной цифры, определяющей порядковый номер стандарта в данной группе;
двузначной цифры (после тире), указывающей год регистрации стандарта.
Пример обозначения
стандарта ЕСКД "Изображения - виды, разрезы, сечения":
ГОСТ
2.
3
- 68
05
категория нормативно-технического документа
класс (стандарты) ЕСКД
классификационная группа стандартов
порядковый номер стандарта
год регистрации стандарта
Обозначение стандартов ЕСКД строится на классификационном принципе.
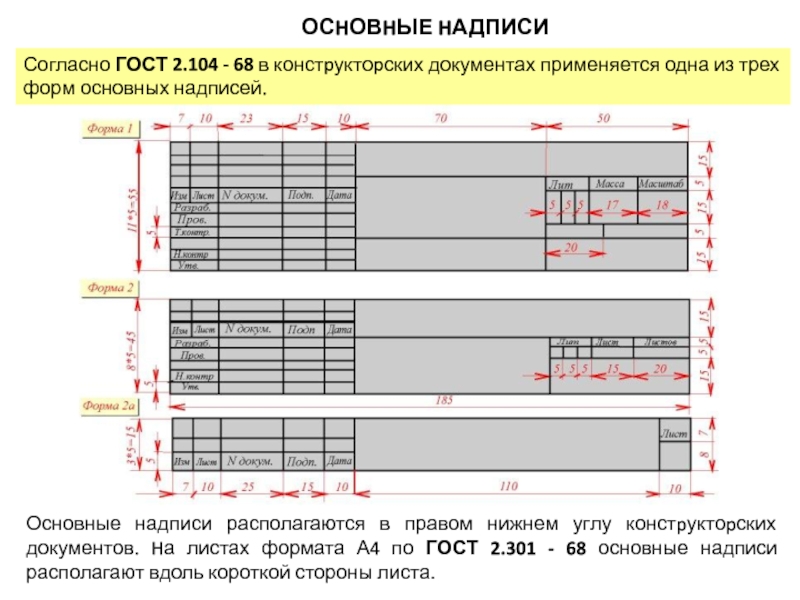
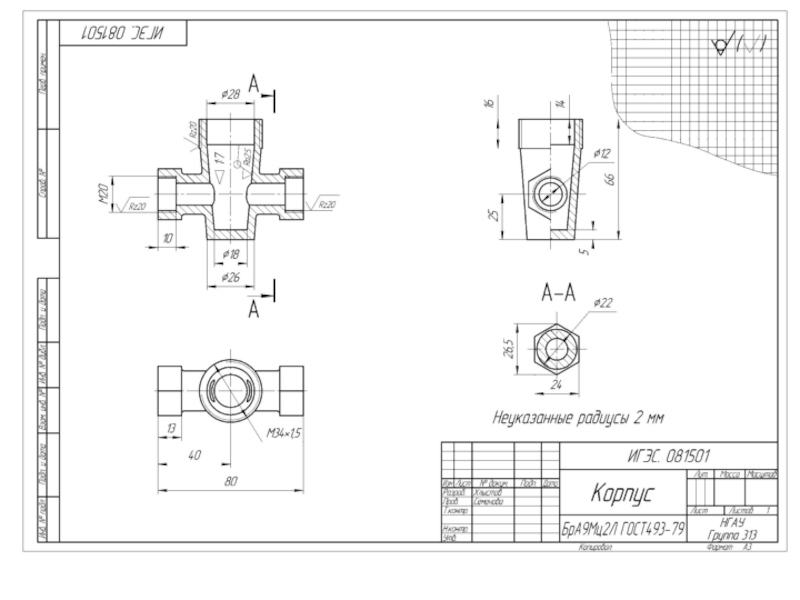
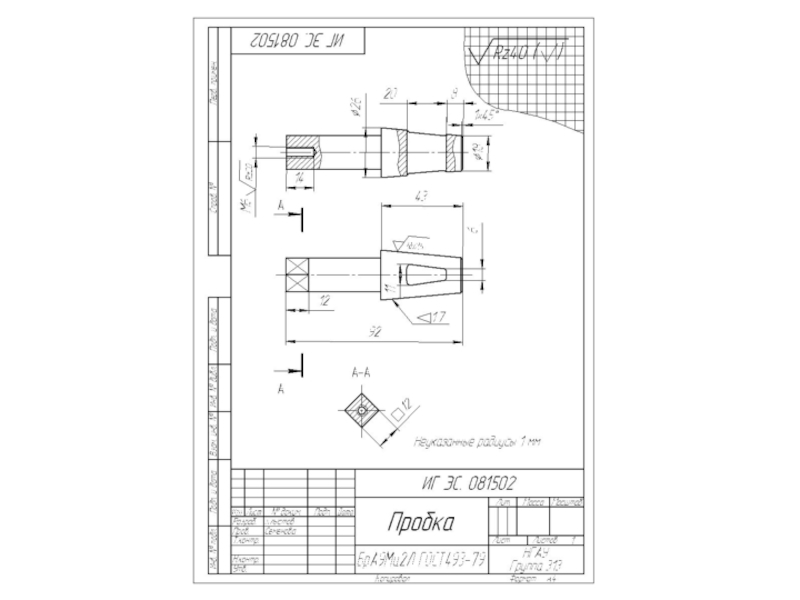
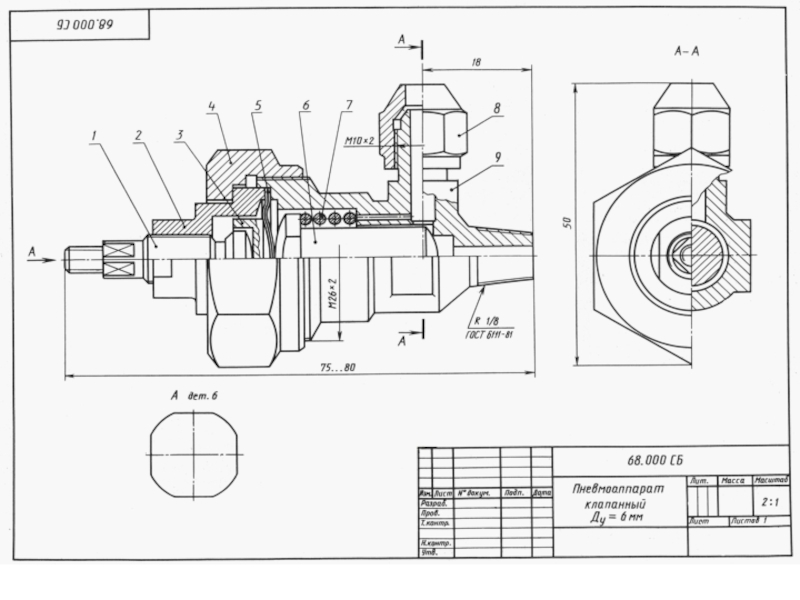
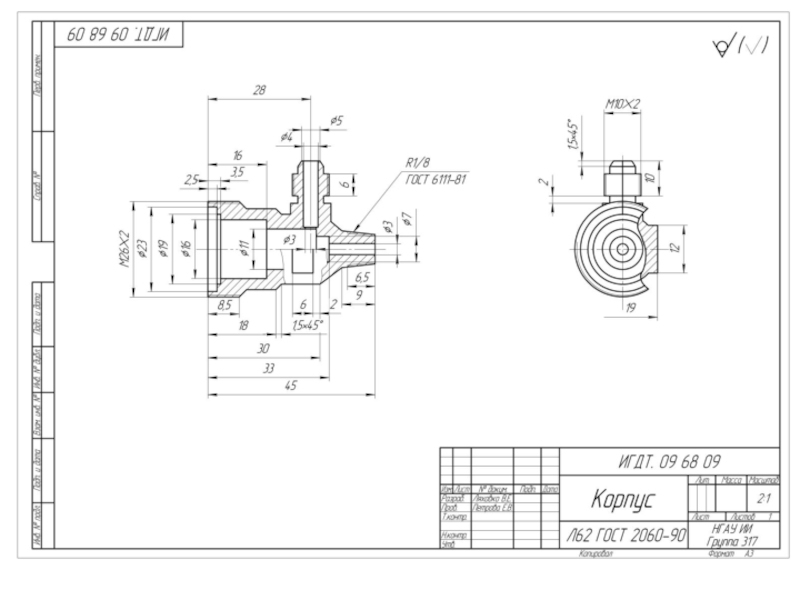
Слайд 7Согласно ГОСТ 2.104 - 68 в констpуктоpских документах применяется одна
из трех форм основных надписей.
ОСHОВHЫЕ HАДПИСИ
Основные надписи располагаются
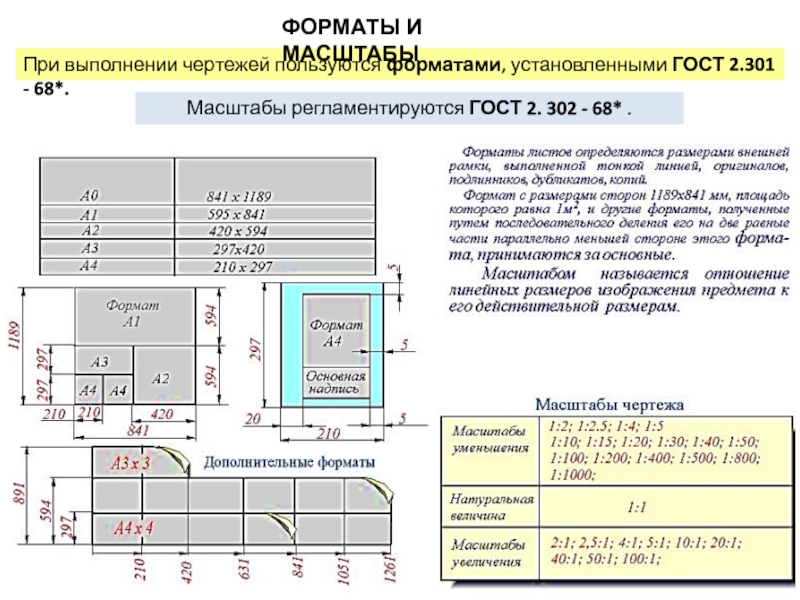
в правом нижнем углу констpуктоpских документов. Hа листах формата А4 по ГОСТ 2.301 - 68 основные надписи располагают вдоль короткой стороны листа. Слайд 8При выполнении чертежей пользуются форматами, установленными ГОСТ 2.301 - 68*.
ФОРМАТЫ И МАСШТАБЫ
Масштабы регламентируются ГОСТ 2. 302 - 68* .
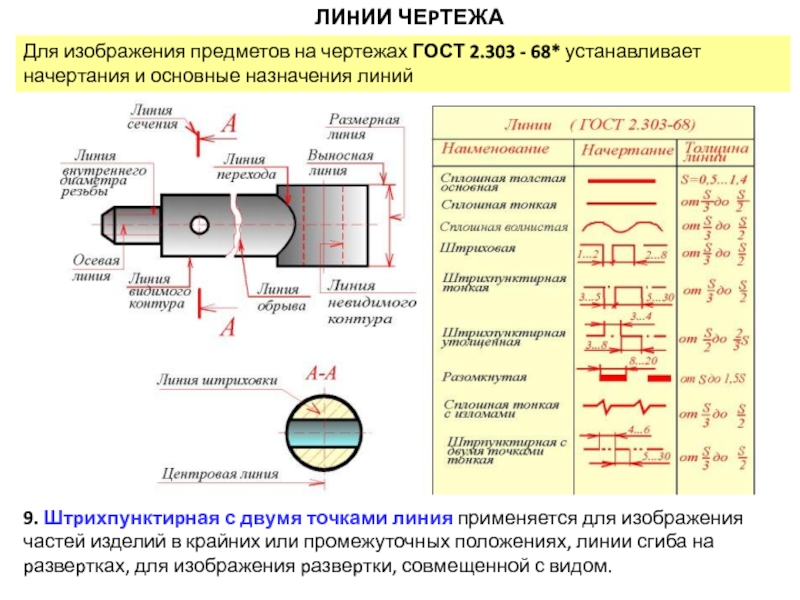
Слайд 91. Сплошная толстая основная линия применяется для изображения видимого контура
предмета, контура вынесенного сечения и входящего в состав pазpеза.
ЛИHИИ ЧЕPТЕЖА
Для изображения предметов на чертежах ГОСТ 2.303 - 68* устанавливает начертания и основные назначения линий
2. Сплошная тонкая линия применяется для изображения pазмеpных и выносных линий, штриховки сечений, линий контура наложенного сечения, линий-выносок, линий для изображения пограничных деталей.
3. Сплошная волнистая линия применяется для изображения линий обрыва, линий pазгpаничения вида и pазpеза.
4. Штриховая линия применяется для изображения невидимого контура. Длина штрихов должна быть одинаковая.
5. Штpихпунктиpная тонкая линия применяется для изображения осевых и центровых линий, линий сечения, являющихся осями симметрии для наложенных или вынесенных сечений.
6. Штpихпунктиpная утолщенная линия применяется для изображения элементов, расположенных перед секущей плоскостью ("наложенная проекция"), линий, обозначающих поверхности, подлежащие теpмообpаботке или покрытию.
7. Разомкнутая линия применяется для обозначения линии сечения.
8. Сплошная тонкая с изломами линия применяется при длинных линиях обрыва.
9. Штpихпунктиpная с двумя точками линия применяется для изображения частей изделий в крайних или промежуточных положениях, линии сгиба на pазвеpтках, для изображения pазвеpтки, совмещенной с видом.
Слайд 10Основным паpаметpом шрифта является его pазмеp h - высота прописных
букв в миллиметрах.
Стандартом установлены следующие pазмеpы шрифта: 2,5; 3,5;
5; 7; 10; 20; 28; 40. ШPИФТЫ ЧЕPТЕЖHЫЕ
Надписи на чертежах выполняют стандартным шрифтом согласно ГОСТ 2.304 - 81.
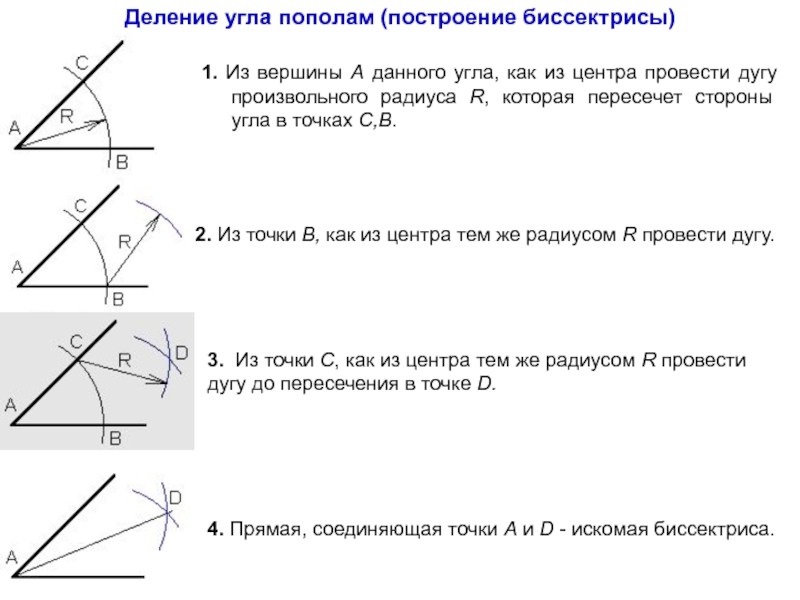
Слайд 12Деление угла пополам (построение биссектрисы)
2. Из точки B, как из
центра тем же радиусом R провести дугу.
1. Из вершины
А данного угла, как из центра провести дугу произвольного радиуса R, которая пересечет стороны угла в точках C,B.3. Из точки С, как из центра тем же радиусом R провести дугу до пересечения в точке D.
4. Прямая, соединяющая точки A и D - искомая биссектриса.
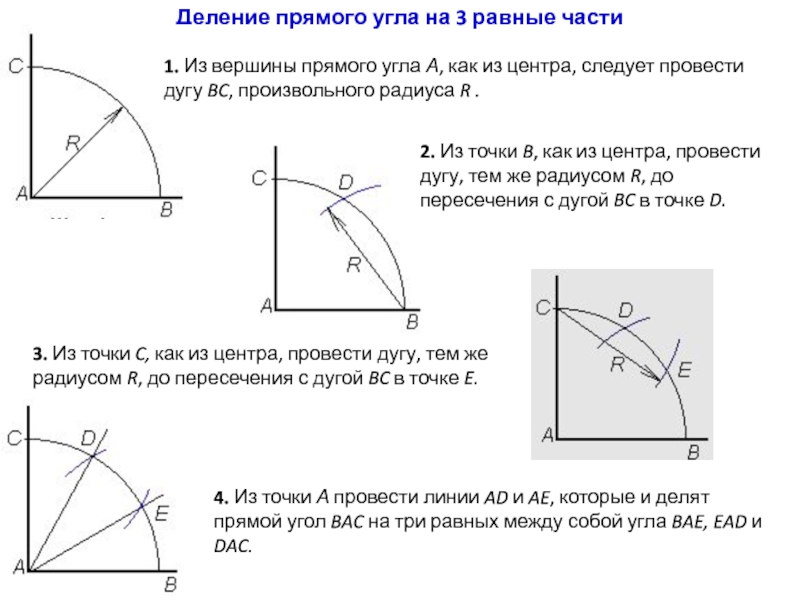
Слайд 13Деление прямого угла на 3 равные части
3. Из точки C,
как из центра, провести дугу, тем же радиусом R, до
пересечения с дугой BC в точке E.4. Из точки А провести линии AD и AE, которые и делят прямой угол BAC на три равных между собой угла BAE, EAD и DAC.
1. Из вершины прямого угла А, как из центра, следует провести дугу BC, произвольного радиуса R .
2. Из точки B, как из центра, провести дугу, тем же радиусом R, до пересечения с дугой BC в точке D.
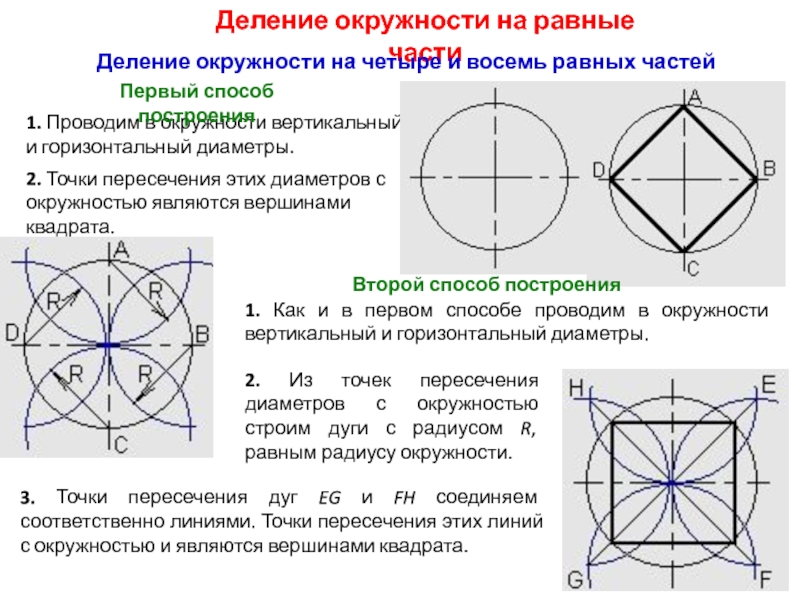
Слайд 14Деление окружности на равные части
Деление окружности на четыре и восемь равных
частей
1. Проводим в окружности вертикальный и горизонтальный диаметры.
2. Точки пересечения
этих диаметров с окружностью являются вершинами квадрата.Первый способ построения
Второй способ построения
1. Как и в первом способе проводим в окружности вертикальный и горизонтальный диаметры.
2. Из точек пересечения диаметров с окружностью строим дуги с радиусом R, равным радиусу окружности.
3. Точки пересечения дуг EG и FH соединяем соответственно линиями. Точки пересечения этих линий с окружностью и являются вершинами квадрата.
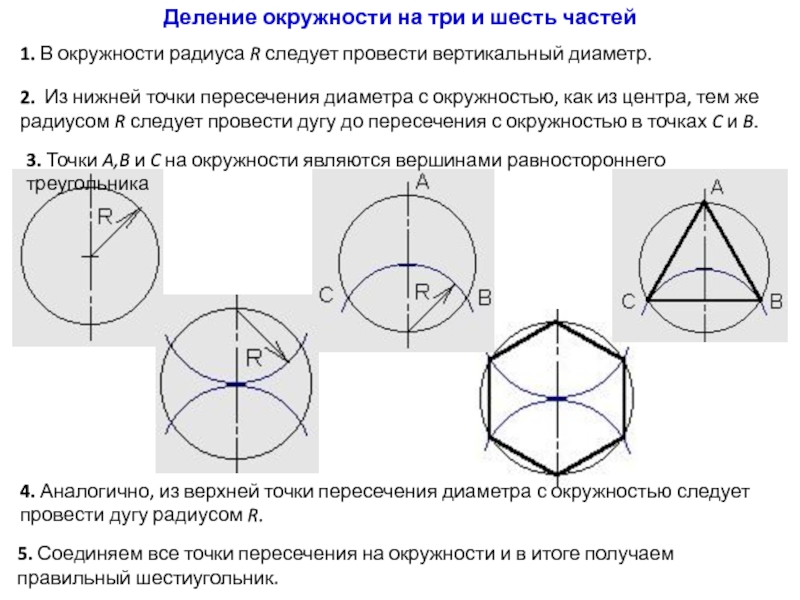
Слайд 15Деление окружности на три и шесть частей
1. В окружности радиуса
R следует провести вертикальный диаметр.
2. Из нижней точки пересечения диаметра
с окружностью, как из центра, тем же радиусом R следует провести дугу до пересечения с окружностью в точках C и B. 3. Точки A,B и C на окружности являются вершинами равностороннего треугольника
5. Соединяем все точки пересечения на окружности и в итоге получаем правильный шестиугольник.
4. Аналогично, из верхней точки пересечения диаметра с окружностью следует провести дугу радиусом R.
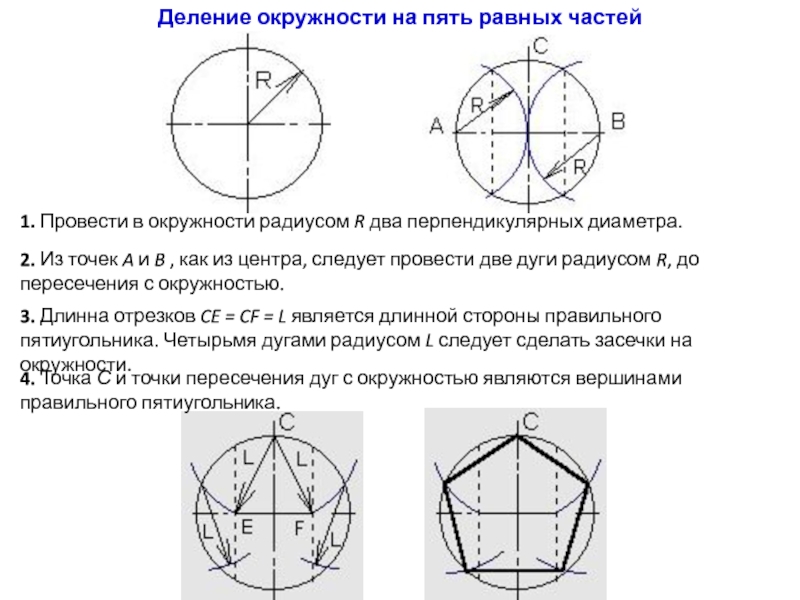
Слайд 16Деление окружности на пять равных частей
1. Провести в окружности радиусом
R два перпендикулярных диаметра.
2. Из точек A и B
, как из центра, следует провести две дуги радиусом R, до пересечения с окружностью.3. Длинна отрезков CE = CF = L является длинной стороны правильного пятиугольника. Четырьмя дугами радиусом L следует сделать засечки на окружности.
4. Точка С и точки пересечения дуг с окружностью являются вершинами правильного пятиугольника.
Слайд 17Сопряжением называется плавный переход одной линии в другую, места перехода
называются точками сопряжения.
Для построения сопряжений надо найти центр сопряжения и
точки сопряжений. Рассмотрим различные типы сопряжений.
R
R
R
n1
O1
n
Скругление острого угла дугой радиуса R можно выполнить в следующей последовательности:
Геометрическим местом точек, равноудаленных от сторон угла, будут являться прямые, параллельные сторонам угла и проходящие от них на расстоянии R;
2. Точка пересечение этих прямых определяет центр скругления О1;
O
3. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения n и n1;
4. Поводим дугу nn1 из центра О1 радиусом R.
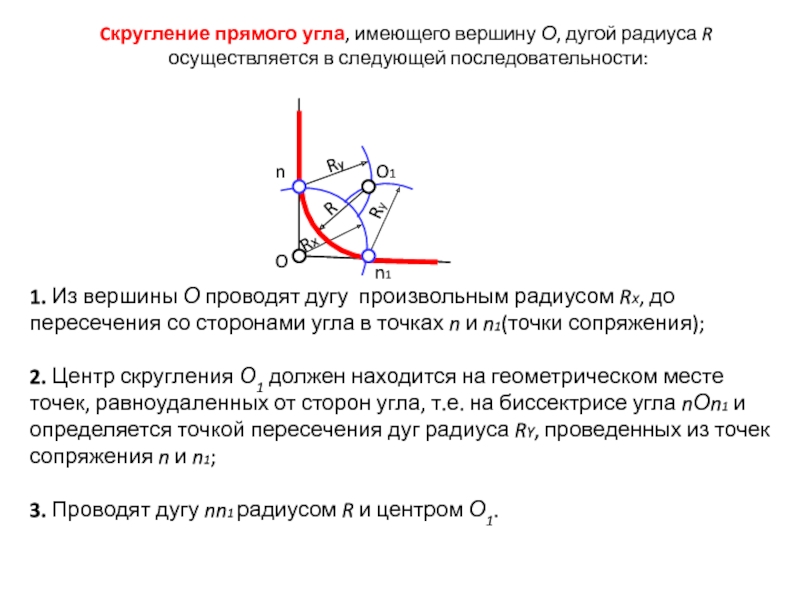
Слайд 181. Из вершины О проводят дугу произвольным радиусом Rх, до
пересечения со сторонами угла в точках n и n1(точки сопряжения);
2. Центр скругления О1 должен находится на геометрическом месте точек, равноудаленных от сторон угла, т.е. на биссектрисе угла nОn1 и определяется точкой пересечения дуг радиуса RY, проведенных из точек сопряжения n и n1;
3. Проводят дугу nn1 радиусом R и центром О1.
n
R
Ry
Rx
O1
Ry
Cкругление прямого угла, имеющего вершину О, дугой радиуса R
осуществляется в следующей последовательности:
O
n1
Слайд 19O
O1
r
R+r
R
r
n
n1
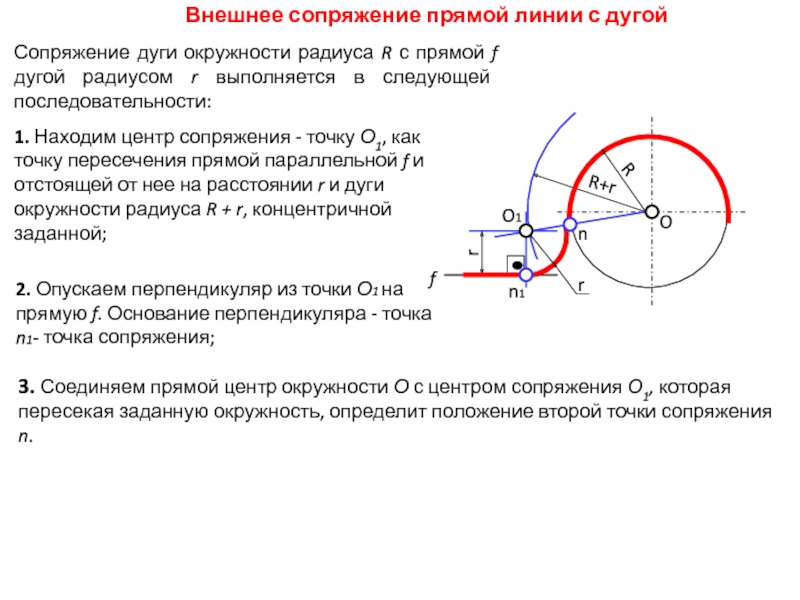
Внешнее сопряжение прямой линии с дугой
3. Соединяем прямой центр окружности
О с центром сопряжения О1, которая пересекая заданную окружность, определит
положение второй точки сопряжения n.f
Сопряжение дуги окружности радиуса R с прямой f дугой радиусом r выполняется в следующей последовательности:
1. Находим центр сопряжения - точку О1, как точку пересечения прямой параллельной f и отстоящей от нее на расстоянии r и дуги окружности радиуса R + r, концентричной заданной;
2. Опускаем перпендикуляр из точки О1 на прямую f. Основание перпендикуляра - точка n1- точка сопряжения;
Слайд 20R2
n
O
O1
O2
R1
R1+R2
n1
R+R2
R
L
L1
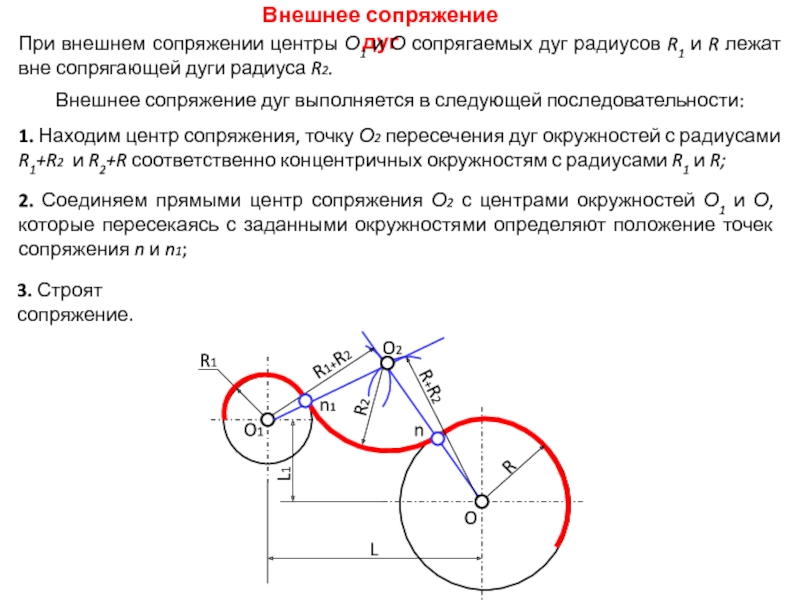
2. Соединяем прямыми центр сопряжения О2 с центрами окружностей О1
и О, которые пересекаясь с заданными окружностями определяют положение точек
сопряжения n и n1;Внешнее сопряжение дуг
При внешнем сопряжении центры О1 и О сопрягаемых дуг радиусов R1 и R лежат вне сопрягающей дуги радиуса R2.
Внешнее сопряжение дуг выполняется в следующей последовательности:
1. Находим центр сопряжения, точку О2 пересечения дуг окружностей с радиусами R1+R2 и R2+R соответственно концентричных окружностям с радиусами R1 и R;
3. Строят сопряжение.
Слайд 21Лекальными кривыми называются плоские кривые, вычерчиваемые при помощи лекал по
предварительно найденным точкам
Парабола
Синусоида
Эвольвента
Циклоида
Эллипс
Парабола
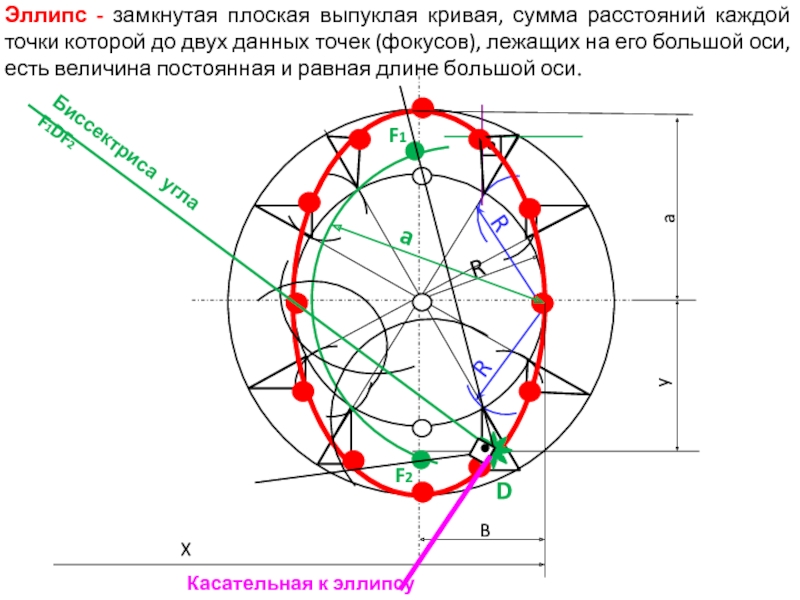
Слайд 22Эллипс - замкнутая плоская выпуклая кривая, сумма расстояний каждой точки
которой до двух данных точек (фокусов), лежащих на его большой
оси, есть величина постоянная и равная длине большой оси.R
R
R
B
X
a
a
y
F2
F1
D
Биссектриса угла F1DF2
Касательная к эллипсу
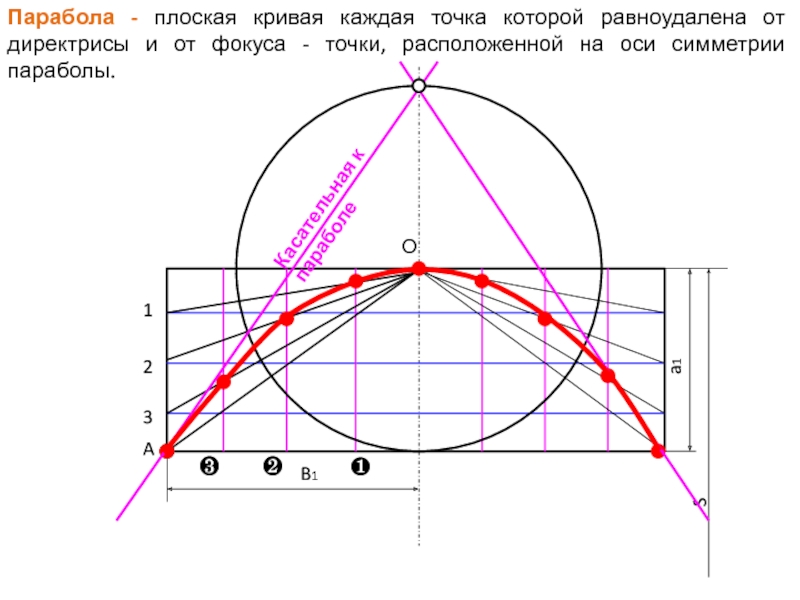
Слайд 23Парабола - плоская кривая каждая точка которой равноудалена от директрисы
и от фокуса - точки, расположенной на оси симметрии параболы.
S
a1
B1
A
Касательная
к параболеО
1
2
3
❶
❷
❸
Слайд 24Косинусоида (синусоида) - плоская кривая, выражающая закон изменения косинуса в
зависимости от изменения величины центрального угла.
А
d1
1
2
3
4
5
6
Слайд 25Эвольвента - траектория точки прямой линии, когда эта прямая перекатывается
без скольжения по окружности.
o
x
y
x
y
0
1
2
3
4
5
6
7
Слайд 26Циклоида - траектория (путь) точки, лежащей на окружности, которая катится
без скольжения по прямой ОО.
О
0
1
3
4
5
6
7
8
9
10
11
2
О1
О2
О3
О4
О5
О6
О7
О8
О9
О10
О11
О