Слайд 1ИССЛЕДОВАНИЕ ФУНКЦИИ
И ПОСТРОЕНИЕ ГРАФИКА
Слайд 2ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
1. НЕПРЕРЫВНОСТЬ, ТОЧКИ РАЗРЫВА ФУНКЦИИ
О
п р е д е л е н и е
1. Функция называется непрерывной в точке , принадлежащей области определения , если функция имеет в точке
конечный предел, равный числу , то есть
О п р е д е л е н и е 2. Функция называется непрерывной справа (слева) в точке из , если в точке существует конечный правый (левый) предел функции , равный числу , то есть
(1)
Слайд 3ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Из свойств предела вытекает следующее утверждение.
Т
е о р е м а 1. Функция
непрерывна в точке a тогда и только тогда, когда в этой точке справедливы равенства:
Слайд 4ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
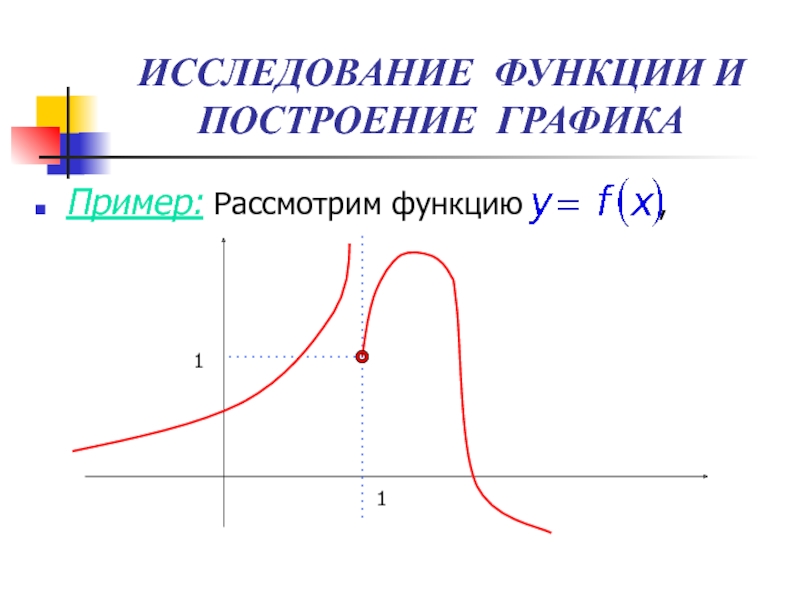
Пример: Рассмотрим функцию
,
1
1
Слайд 5ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
О п р е д е
л е н и е 3. Функция
называется непрерывной в интервале , если она непрерывна в любой его точке.
Функция называется непрерывной на отрезке , если она непрерывна в интервале , непрерывна справа в точке непрерывна слева в точке .
Слайд 6ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Т е о р е м
а 2. Если функция дифференцируема в точке ,
то она непрерывна в этой точке. Обратное утверждение неверно.
О п р е д е л е н и е 4. Точка , являю-щаяся предельной точкой множества , называется точкой разрыва функции , если в точке эта функция либо не определена, либо определена, но нарушено условие непрерывности.
Слайд 7ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
О п р е д е
л е н и е 5. Точка разрыва
называется точкой устранимого разрыва функции , если в этой точке предел функции существует, но в точке либо не определена, либо значение не совпадает с найденным пределом, то есть
Пример Функция
при х =0
при х =0
Имеет в точке х=0 устранимый разрыв, т.к:
Слайд 8ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
О п р е д е
л е н и е 6. Точка разрыва
называется точкой разрыва первого рода функции , если в этой точке функция имеет конечные, но не равные друг другу правый и левый пределы, то есть:
Пример:
«знак» числа х имеет в точке х=0 разрыв первого рода, т.к:
Слайд 9ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
у
х
1
-1
0
О
п р е д е л е н и е
7. Точка разрыва
называется точкой разрыва второго рода функции
если в этой точке функция не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов равен бесконечности.
Слайд 10ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
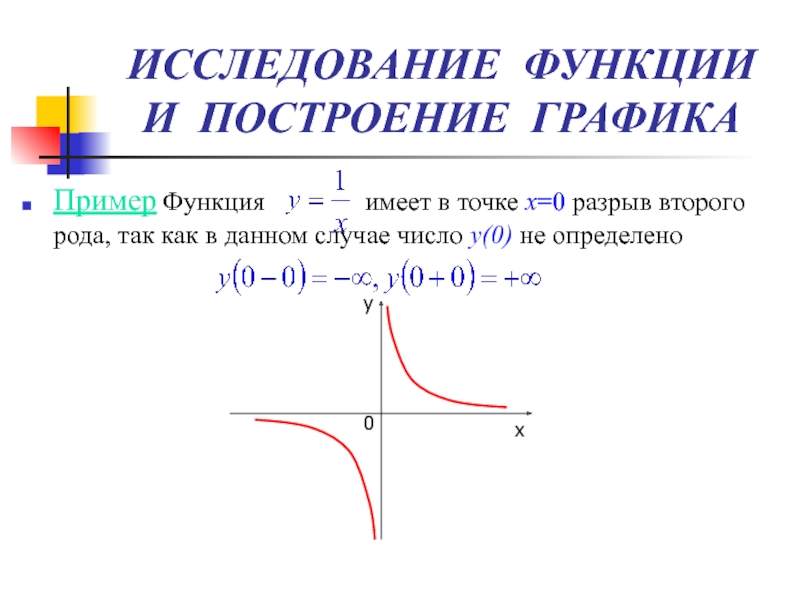
Пример Функция
имеет в точке х=0 разрыв второго рода,
так как в данном случае число y(0) не определено
у
х
0
Слайд 11ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Т е о р е м
а 3. Если функция
непрерывна в точке и существует конечный предел , то справедливо равенство:
Т е о р е м а 4. Пусть функция непрерывна в точке
и функция непрерывна в точке Тогда сложная функция непрерывна в точке .
Т е о р е м а 5. Сумма, разность, произведение, частное, суперпозиция конечного числа непрерывных функций (то есть любая элементарная функция) есть функция, непрерывная во всех точках области определения.
Слайд 12ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
2. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
О п р
е д е л е н и е 8.
Прямая называется верти-кальной асимптотой кривой , если точка является для функции точкой разрыва второго рода.
О п р е д е л е н и е 9. Прямая называется наклонной асимптотой кривой на (на ), если
Слайд 13ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Т е о р е м
а 6. Кривая
имеет наклонную асимптоту на (на ) тогда и только тогда, когда существуют конечные пределы:
Пример Найти асимптоты графика функции:
Область определения:
непрерывна во всех точках области определения,
Слайд 14ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
1.Найдем вертикальные асимптоты графика:
Точка х =
-1является точкой разрыва второго рода, значит прямая х = -1является
вертикальной асимптотой графика
2. Найдем наклонную асимптоту на . Вычислим:
Слайд 15ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Наклонной асимптотой является прямая:
Ответ: х =
-1 - вертикальная асимптота
y =
x -3- наклонная асимптота при и
Слайд 16ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
3. ВОЗРАСТАНИЕ, УБЫВАНИЕ, ЭКСТРЕМУМЫ ФУНКЦИИ
О
п р е д е л е н и е
10. Функция называется возрастающей (убывающей) в некотором промежутке, если для любых и из этого промежутка, удовлетворяющих условию выполняется неравенство:
Слайд 17ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
О п р е д е
л е н и е 11. Точки области определения функции,
в которых производная равна нулю или не существует, называются критическими.
О п р е д е л е н и е 12. Пусть функция определена всюду в некоторой окрестности точки . Точка называется точкой максимума (минимума) функции , если существует такая окрестность с центром в точке , что справедливо неравенство:
О п р е д е л е н и е 13. Максимумы и минимумы функции называются экстремумами функции.
Слайд 18ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Т е о р е м
а 7 (достаточное условие возрастания (убывания)). Пусть во всех точках
некоторого интервала функция дифференцируема и Тогда в этом интервале функция возрастает (убывает).
Т е о р е м а 8 (необходимое условие экстремума). Если функция имеет экстремум в точке , то эта точка критическая.
Слайд 19ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
Т е о р е м
а 9 (достаточное условие экстремума). Пусть функция
дифференцируема в некоторой окрестности критической точки за исключением, быть может, самой этой точки. Если в пределах указанной окрестности функция
имеет разные знаки слева и справа от точки , то точка экстремума. Если при этом знак производной меняется
с «» на «+», то точка минимума,
с «+» на «», то точка максимума.
Если в пределах указанной окрестности функция имеет один и тот же знак слева и справа от точки , то в экстремума нет.
Слайд 20ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
П р и м е р.
Найти интервалы возрастания, убывания и экстремумы функции:
Р е ш
е н и е. 1) Функция определена
2) Найдем производную
при и
Слайд 21ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА
4
знак
вывод о
+
+
-
Возраст.
Возраст.
убывает
max
min
О т в е т: интервалы возрастания:
интервалы убывания: