Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История математики
Содержание
- 1. История математики
- 2. История математики
- 3. В истории математики традиционно выделяются несколько этапов развития математических знаний:
- 4. Формирование понятия геометрической фигуры и числа как
- 5. Изобретение арифметических операций. Накопление эмпирическим путём (методом
- 6. Появление в древней Греции дедуктивной математической системы,
- 7. Математики стран ислама не только сохранили античные
- 8. В XVI—XVIII веках возрождается и уходит далеко
- 9. В XIX—XX веках становится понятно, что взаимоотношение
- 10. Содержание 1 Возникновение арифметики и геометрии2 Древний Восток
- 11. Возникновение арифметики и геометрии
- 12. Математика в системе человеческих знаний есть раздел,
- 13. аддитивным (один+на+дцать, XXX = 30)субтрактивным (IX, девя-но-сто)мультипликативным (пять*десят, три*ста)
- 14. Для запоминания результатов счёта использовали зарубки, узелки
- 15. Когда понятие абстрактного числа окончательно утвердилось, следующей
- 16. Математика в Древнем Египте
- 17. Древнейшие древнеегипетские математические тексты относятся к началу
- 18. Основные сохранившиеся источники: папирус Ахмеса, он же
- 19. В области геометрии египтяне знали точные формулы
- 20. Египтяне знали точные формулы для объёма параллелепипеда
- 21. Вавилонская математика
- 22. Вавилоняне писали клинописными значками на глиняных табличках,
- 23. Математика В Древнем Китае
- 24. Цифры в древнем Китае обозначались специальными иероглифами,
- 25. Математика в Древней Греции
- 26. Математика в современном понимании этого слова родилась
- 27. Греки подошли к делу с другой стороны.Во-первых,
- 28. Во-вторых, для открытия таких истин пифагорейцы разработали
- 29. Попытка пифагорейцев положить в основу мировой гармонии
- 30. История математики в Индии
- 31. Индийская нумерация (способ записи чисел) изначально была
- 32. Математика исламского средневековья
- 33. Математика Востока, в отличие от греческой, всегда
- 34. Западная Европа
- 35. Средневековье, IV—XV века С XIV века главным
- 36. Первым крупным математиком средневековой Европы стал в
- 37. XVI век XVI век стал переломным для
- 38. XVI века — изобретение логарифмов Джон Непер
- 39. В 1585 году фламандец Симон Стевин издаёт
- 40. XVII век В XVII веке быстрое развитие
- 41. В конце XVII века идея неделимых была
- 42. XVIII век XVIII век в математике можно
- 43. Далеко продвинулись теория и техника интегрирования. Входят
- 44. Стремительно развивается линейная алгебра. Первое подробное описание
- 45. Теория вероятностей перестаёт быть экзотикой и доказывает
- 46. XIX век В геометрии, алгебре, анализе появляются
- 47. Неевклидовы геометрии
- 48. Геометрия Если XVIII век был веком анализа,
- 49. Дифференциальная геометрия получила мощный толчок после выхода
- 50. Во второй половине XIX века наконец привлекает
- 51. Математический анализ Анализ в XIX веке развивался
- 52. Алгебра и теория чисел У. Гамильтон открыл
- 53. Формируется понятие линейного пространства (Грассман и, 1843—1844).
- 54. Теория вероятностей На первое место выходят теория
- 55. Математическая логика В работе «Формальная логика» (1847)
- 56. XX век: основные достижения Престиж профессии математика
- 57. Новые направления В 1900 году Давид Гильберт
- 58. Различные разделы дискретной математики.Информатика и кибернетика.Методы математической
- 59. Бурно развивались и многие «старые» области математики.Абстрактная
- 60. Среди наиболее выдающихся математиков XX века можно
- 61. Список использованной литературы:Глейзер Г. И. История математики
- 62. Спасибо за внимание!
- 63. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Работу выполнила:
Cernikova Elisaveta.
Преподователь:Градежда Леся Дмитриевна.
МОУ Раменского р-на СОШ №6
Контактная информация:89853806863.Клязменский
пр.д.9
Слайд 4Формирование понятия геометрической фигуры и числа как идеализации реальных объектов
и множеств однородных объектов. Появление счёта и измерения, которые позволили
сравнивать различные числа, длины, площади и объёмы.Слайд 5Изобретение арифметических операций. Накопление эмпирическим путём (методом проб и ошибок)
знаний о свойствах арифметических действий, о способах измерения площадей и
объёмов простых фигур и тел. В этом направлении далеко продвинулись шумеро-вавилонские, китайские и индийские математики древности.Слайд 6Появление в древней Греции дедуктивной математической системы, показавшей, как получать
новые математические истины на основе уже имеющихся. Венцом достижений древнегреческой
математики стали «Начала» Евклида, игравшие роль стандарта математической строгости в течение двух тысячелетий.Слайд 7Математики стран ислама не только сохранили античные достижения, но и
смогли осуществить их синтез с открытиями индийских математиков, которые в
теории чисел продвинулись дальше греков.Слайд 8В XVI—XVIII веках возрождается и уходит далеко вперёд европейская математика.
Её концептуальной основой в этот период являлась уверенность в том,
что математические модели являются своего рода идеальным скелетом Вселенной, и поэтому открытие математических истин является одновременно открытием новых свойств реального мира. Главным успехом на этом пути стала разработка математических моделей зависимости переменных величин (функция) и общая теория движения (анализ бесконечно малых). Все естественные науки были перестроены на базе новооткрытых математических моделей, и это привело к колоссальному их прогрессу.Слайд 9В XIX—XX веках становится понятно, что взаимоотношение математики и реальности
далеко не столь просто, как ранее казалось. Не существует общепризнанного
ответа на своего рода «основной вопрос философии математики»: найти причину «непостижимой эффективности математики в естественных науках». В этом, и не только в этом, отношении математики разделились на множество дискутирующих школ. Наметилось несколько опасных тенденций: чрезмерно узкая специализация, изоляция от практических задач и др. В то же время мощь математики и её престиж, поддержанный эффективностью применения, высоки как никогда прежде.Слайд 10Содержание
1 Возникновение арифметики и геометрии
2 Древний Восток
2.1 Египет
2.2 Вавилон
2.3
Китай
3 Древняя Греция
4 Индия
5 Страны ислама
6 Западная Европа
6.1 Средневековье,
IV—XV века6.2 XVI век
6.3 XVII век
6.4 XVIII век
6.5 XIX век
6.5.1 Геометрия
6.5.2 Математический анализ
6.5.3 Алгебра и теория чисел
6.5.4 Теория вероятностей
6.5.5 Математическая логика
8 XX век: основные достижения
8.1 Новые направления
Слайд 12Математика в системе человеческих знаний есть раздел, занимающийся такими понятиями,
как количество, структура, соотношение и т. п. Развитие математики началось с создания
практических искусств счёта и измерения линий, поверхностей и объёмов.Понятие о натуральных числах формировалось постепенно и осложнялось неумением первобытного человека отделять числовую абстракцию от её конкретного представления. Вследствие этого счёт долгое время оставался только вещественным — использовались пальцы, камешки, пометки и т. п. Археолог Б. А. Фролов обосновывает существование счёта уже в верхнем палеолите.С распространением счёта на крупные количества появилась идея считать не только единицами, но и, так сказать, пакетами единиц, содержащими, например, 10 объектов. Эта идея немедленно отразилась в языке, а затем и в письменности. Принцип именования или изображения числа («нумерация») может быть
Слайд 13аддитивным (один+на+дцать, XXX = 30)
субтрактивным (IX, девя-но-сто)
мультипликативным (пять*десят, три*ста)
Слайд 14Для запоминания результатов счёта использовали зарубки, узелки и т. д. С изобретением
письменности стали использовать буквы или особые значки для сокращённого изображения
больших чисел. При таком кодировании обычно воспроизводился тот же принцип нумерации, что и в языке.Слайд 15Когда понятие абстрактного числа окончательно утвердилось, следующей ступенью стали операции
с числами. Натуральное число — это идеализация конечного множества воднородных, устойчивых
и неделимых предметов (людей, овец, дней и т. п.). Для счёта нужно иметь математические модели таких важных событий, как объединение нескольких множеств в одно или, наоборот, отделение части множества. Так появились операции сложения и вычитания. Умножение для натуральных чисел появилось в качестве, так сказать, пакетного сложения. Свойства и взаимосвязь операций открывались постепенно.Слайд 17Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до
н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве
домов, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому в настоящее время знаний о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов, что подтверждается тем, что греческие математики учились у египтянСлайд 18Основные сохранившиеся источники: папирус Ахмеса, он же папирус Ринда (84
математические задачи), и московский папирус Голенищева (25 задач), оба из
Среднего царства, времени расцвета древнеегипетской культуры. Авторы текста нам неизвестны.Иероглифическая запись уравнения
Слайд 19В области геометрии египтяне знали точные формулы для площади прямоугольника,
треугольника и трапеции. Площадь произвольного четырёхугольника со сторонами a, b,
c, d вычислялась приближённо как ; эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику. Площадь круга вычислялась, исходя из предположения = 3,1605 (погрешность менее 1 %).Слайд 20Египтяне знали точные формулы для объёма параллелепипеда и различных цилиндрических
тел, а также пирамиды и усечённой пирамиды. Пусть мы имеем
правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по оригинальной, но точной формуле: .Слайд 22Вавилоняне писали клинописными значками на глиняных табличках, которые в немалом
количестве дошли до наших дней (более 500 тыс., из них
около 400 связаны с математикой). Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Отметим, что корни культуры вавилонян были в значительной степени унаследованы от шумеров — клинописное письмо, счётная методика и т. п.Вавилонские цифры
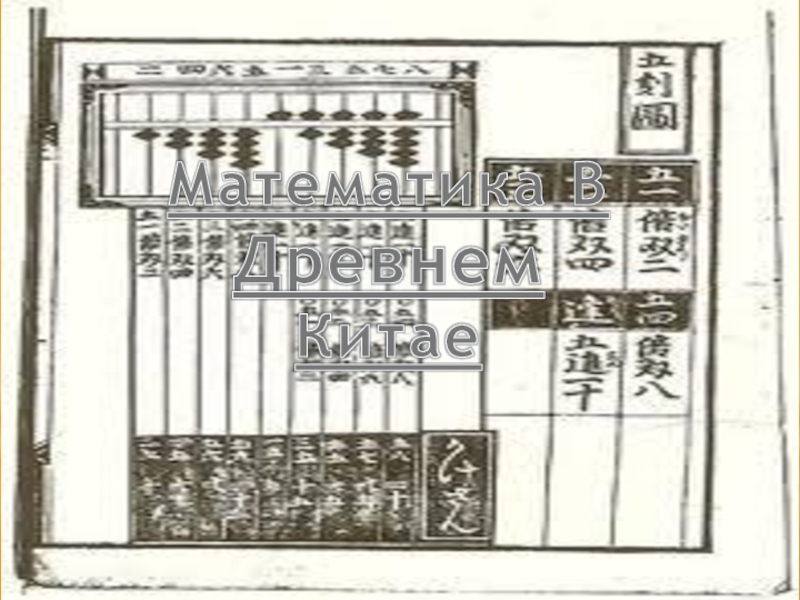
Слайд 24Цифры в древнем Китае обозначались специальными иероглифами, которые появились во
II тысячелетии до н. э., и начертание их окончательно установилось к
III веку до н. э. Эти иероглифы применяются и в настоящее время. Китайский способ записи чисел изначально был мультипликативным. Например, запись числа 1946, используя вместо иероглифов римские цифры, можно условно представить как 1М9С4Х6. Однако на практике расчёты выполнялись на счётной доске, где запись чисел была иной — позиционной, как в Индии, и, в отличие от вавилонян, десятичнойКитайские и Японские счеты
Слайд 26Математика в современном понимании этого слова родилась в Греции. В
странах-современниках Эллады математика использовалась либо для обыденных нужд (подсчёты, измерения),
либо, наоборот, для магических ритуалов, имевших целью выяснить волю богов (астрология, нумерология и т. п.). Математической теории в полном смысле этого слова не было, дело ограничивалось сводом эмпирических правил, часто неточных или даже ошибочных.Слайд 27Греки подошли к делу с другой стороны.
Во-первых, пифагорейская школа выдвинула
тезис «Числа правят миром». Или, как сформулировали эту же мысль
два тысячелетия спустя: «Природа разговаривает с нами на языке математики» (Галилей). Это означало, что истины математики есть в известном смысле истины реального бытия.Пифагор
Слайд 28Во-вторых, для открытия таких истин пифагорейцы разработали законченную методологию. Сначала
они составили список первичных, интуитивно очевидных математических истин (аксиомы, постулаты).
Затем с помощью логических рассуждений (правила которых также постепенно унифицировались) из этих истин выводились новые утверждения, которые также обязаны быть истинными. Так появилась дедуктивная математика.Эвклид
Слайд 29Попытка пифагорейцев положить в основу мировой гармонии целые числа (и
их отношения) была поставлена под сомнение после того, как были
обнаружены иррациональные числа. Платоновская школа (IV век до н. э.) выбрала иной, геометрический фундамент математики (Евдокс Книдский). На этом пути были достигнуты величайшие успехи античной математики (Евклид.Архимед, Аполлоний Пергский и другие).Муза геометрии
Слайд 31Индийская нумерация (способ записи чисел) изначально была изысканной. В санскрите
были средства для именования чисел до 1050. Для цифр сначала
использовалась сиро-финикийская система, а с VI века до н. э. — написание «брахми», с отдельными знаками для цифр 1-9. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими, а сами арабы — индийскими.От этих индийских значков,произошли современные цифры
Слайд 33Математика Востока, в отличие от греческой, всегда носила более практичный
характер. Соответственно наибольшее значение имели вычислительные и измерительные аспекты. Основными
областями применения математики были торговля, строительство, география, астрономия и астрология, механика, оптика.Слайд 35Средневековье, IV—XV века
С XIV века главным местом научного обмена становится
Виз В конце XII века на базе нескольких монастырских школ
был создан Парижский университет, где обучались тысячи студентов со всех концов Европы; почти одновременно возникают Оксфорд и Кембридж антия. . В XII—XIII веках публикуются первые в Европе изложения десятичной позиционной системы записи (сначала переводы ал-Хорезми, потом собственные руководства), и начинается её применение. С XIV века индо-арабские цифры начинают вытеснять римские даже на могильных плитах.Слайд 36Первым крупным математиком средневековой Европы стал в XIII веке Леонардо
Пизанский, известный под прозвищем Фибоначчи. Основной его труд: (1202 год,
второе переработанное издание — 1228 год). Абаком Леонардо называл арифметические вычисления. В книгах «Арифметика» и «О данных числах» Иордана Неморария усматриваются зачатки символической алгебры, до поры до времени не отделившейся от геометрииВ XIV веке университеты появляются почти во всех крупных странах (Прага, Краков, Вена, Гейдельберг, Лейпциг, Базель и др.).Страница из «Книга абака»
Слайд 37XVI век
XVI век стал переломным для европейской математики. Полностью усвоив
достижения предшественников, она несколькими мощными рывками вырвалась далеко вперёд. Первым
крупным достижением стало открытие общего метода решения уравнений третьей и четвёртой степени. Итальянские математики дель Ферро, Тарталья и Феррари решили проблему, с которой несколько веков не могли справиться лучшие математики мира.При этом обнаружилось, что в решении иногда появлялись «невозможные» корни из отрицательных чисел. После анализа ситуации европейские математики назвали эти корни «мнимыми числами» и выработали правила обращения с ними, приводящие к правильному результату. Так в математику впервые вошли комплексные числа.Слайд 39В 1585 году фламандец Симон Стевин издаёт книгу «Десятая» о
правилах действий с десятичными дробями, после чего десятичная система одерживает
окончательную победу и в области дробных чисел. Стевин также провозгласил полное равноправие рациональных и иррациональных чисел, а также (с некоторыми оговорками) и отрицательных чисел.Слайд 40XVII век
В XVII веке быстрое развитие математики продолжается, и к
концу века облик науки коренным образом меняется. Рене Декарт исправляет
стратегическую ошибку античных математиков и восстанавливает алгебраическое понимание числа (вместо геометрического).Слайд 41В конце XVII века идея неделимых была существенно расширена ом
и Лейбницем, и появился исключительно могучий инструмент исследования — математический анализ.
Ньютон
Слайд 42XVIII век
XVIII век в математике можно кратко охарактеризовать как век
анализа, который стал главным объектом приложения усилий математиков. Способствуя бурному
развитию естественных наук, анализ, в свою очередь, прогрессировал сам, получая от них всё более и более сложные задачи. На стыке этого обмена идеями родилась математическая физика.Слайд 43Далеко продвинулись теория и техника интегрирования. Входят в широкое употребление
кратные интегралы (Эйлер, ), причём не только в декартовых координатах.
Появляются и поверхностные интегралы (Лагранж, Гаусс). Усиленно разрабатывается теория дифференциальных уравнений, как обыкновенных, так и в частных производных. Математики проявляют исключительную изобретательность при решении дифференциальных уравнений в частных производных, для каждой задачи изобретая свои методы решения. Сформировалось понятие краевой задачи, возникли первые методы её решения.Лагранж
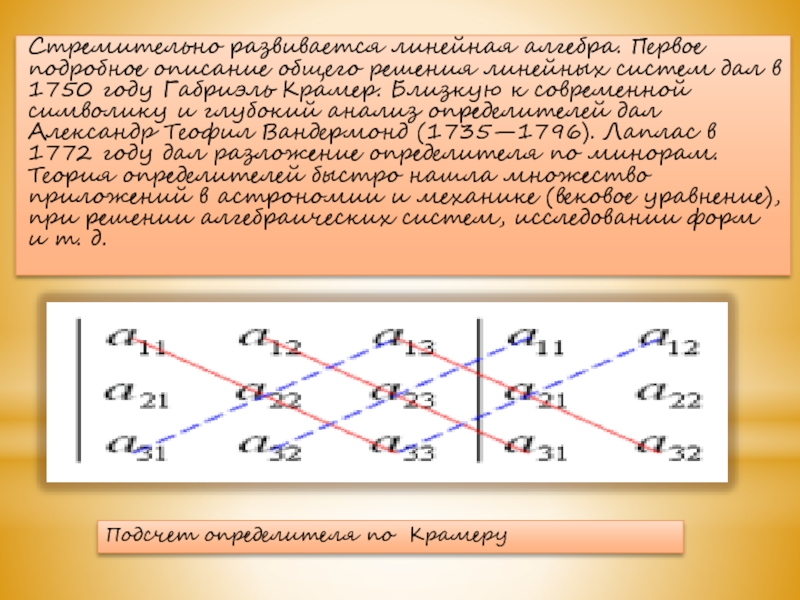
Слайд 44Стремительно развивается линейная алгебра. Первое подробное описание общего решения линейных
систем дал в 1750 году Габриэль Крамер. Близкую к современной
символику и глубокий анализ определителей дал Александр Теофил Вандермонд (1735—1796). Лаплас в 1772 году дал разложение определителя по минорам. Теория определителей быстро нашла множество приложений в астрономии и механике (вековое уравнение), при решении алгебраических систем, исследовании форм и т. д.Подсчет определителя по Крамеру
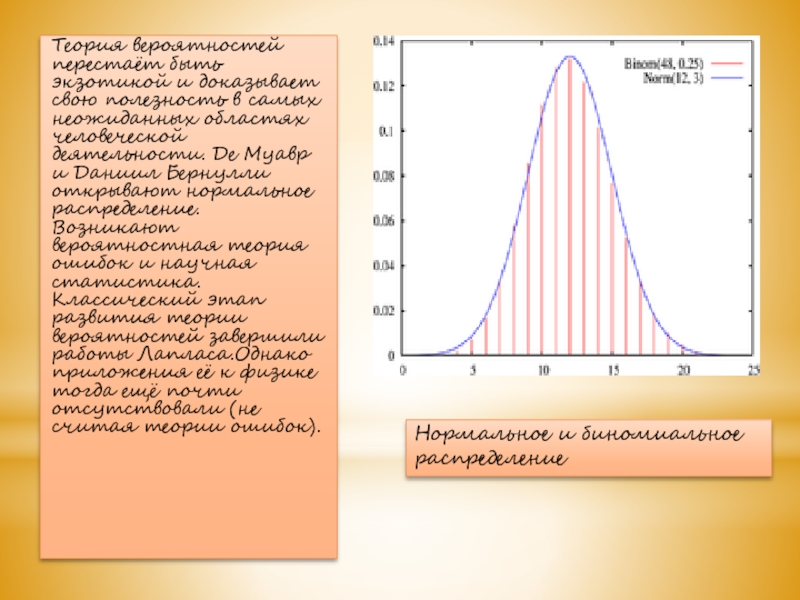
Слайд 45Теория вероятностей перестаёт быть экзотикой и доказывает свою полезность в
самых неожиданных областях человеческой деятельности. Де Муавр и Даниил Бернулли
открывают нормальное распределение. Возникают вероятностная теория ошибок и научная статистика. Классический этап развития теории вероятностей завершили работы Лапласа.Однако приложения её к физике тогда ещё почти отсутствовали (не считая теории ошибок).Нормальное и биномиальное распределение
Слайд 46XIX век
В геометрии, алгебре, анализе появляются многочисленные нестандартные структуры с
необычными свойствами: неевклидовы и многомерные геометрии, кватернионы, конечные поля, некоммутативные
группы и т. п.Объектами математического исследования всё больше становятся нечисловые объекты: события, предикаты, множества, абстрактные структуры, векторы, тензоры, матрицы, функции, многолинейные формы и т. д.
Возникает и получает широкое развитие математическая логика, в связи с чем появилось искушение связать именно с ней коренные основания математики.
Георг Кантор вводит в математику предельно абстрактную теорию множеств, а заодно понятие актуальной бесконечности произвольного масштаба. В конце века при попытке обосновать фундамент математики на основе теории множеств были обнаружены противоречия, которые заставили задуматься над непростыми вопросами: что означает «существование» и «истинность» в математике?
Слайд 48Геометрия
Если XVIII век был веком анализа, то XIX век по
преимуществу стал веком геометрии. Быстро развиваются созданные в конце XVIII
века начертательная геометрия (Монж, Ламберт) и возрождённая проективная геометрия (Монж, Понселе, Лазар Карно). Появляются новые разделы: векторное исчисление и векторный анализ, геометрия Лобачевского, многомерная риманова геометрия, теория групп преобразований. Происходит интенсивная алгебраизация геометрии — в неё проникают методы теории групп, в конце века — топологии, возникает алгебраическая геометрия.Слайд 49Дифференциальная геометрия получила мощный толчок после выхода чрезвычайно содержательного труда
Гаусса «Общие исследования о кривых поверхностях» Крупнейшим достижением стало введение
понятия вектора и векторного поля. Первоначально векторы ввёл У. Гамильтон в связи со своими кватернионами (как их трёхмерную мнимую часть) Компактность и инвариантность векторной символики, использованной в первых трудах Максвелла, заинтересовали физиков; вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному исчислению современный вид.Соприкасающаяся для кривой и три вектора Френе
Слайд 50Во второй половине XIX века наконец привлекает общее внимание геометрия
Тот факт, что даже у классической геометрии существует альтернатива, произвёл
огромное впечатление на весь научный мир. Он также стимулировал переоценку многих устоявшихся стереотипов в математике и физике.Н.К Лобачевский
Слайд 51Математический анализ
Анализ в XIX веке развивался путём быстрой, но мирной
эволюции. Широчайшее развитие получила теория аналитических функций комплексного переменного, Многочисленные
прикладные задачи деятельно стимулировали теорию дифференциальных уравнений, выросшую в обширную и плодотворную математическую дисциплину.Слайд 52Алгебра и теория чисел
У. Гамильтон открыл удивительный некоммутативный мир кватернионов.
Возникла
геометрическая теория чисел
Эварист Галуа, опередивший своё время, представляет глубокий анализ
решения уравнений произвольных степеней. Ключевыми понятиями исследования оказываются алгебраические свойства связанных с уравнением группы подстановок и полей расширения. Галуа завершил работы Абеля, доказавшего, что уравнения степени выше 4-й неразрешимы в радикалах.Слайд 53Формируется понятие линейного пространства (Грассман и, 1843—1844). В 1858 году
Кэли публикует общую теорию матриц, определяет операции над ними, вводит
характеристический многочлен. К 1870 году доказаны все базовые теоремы линейной алгебры, включая приведение к жордановой нормальной форме.В 1871 году Дедекинд вводит понятия кольца, модуля и идеала. Он и Кронекер создают общую теорию делимости.
Кэли
Слайд 54Теория вероятностей
На первое место выходят теория ошибок, статистика и физические
приложения. Этим занимались Гаусс, Пуассон, Коши. Была выявлена важность нормального
распределения как предельного во многих реальных ситуациях.Во всех развитых странах возникают статистические департаменты/общества. Благодаря работам Карла Пирсона возникает математическая статистика с проверкой гипотез и оценкой параметров.
Всё же математические основы теории вероятностей в XIX веке ещё не были созданы, и Гильберт в начале XX века отнёс эту дисциплину к прикладной физике.
Карл Пирсон
Слайд 55Математическая логика
В работе «Формальная логика» (1847) де Морган описал понятие
универсума и символы для логических операторов, записал известные «законы де
Моргана». Позже он ввёл общее понятие математического отношения и операций над отношениями.Слайд 56XX век: основные достижения
Престиж профессии математика стал в XX столетии
заметно выше. Математика развивалась экспоненциально, и невозможно сколько-нибудь полно перечислить
сделанные открытия, но некоторые наиболее серьёзные достижения упомянуты ниже.Слайд 57Новые направления
В 1900 году Давид Гильберт на Международном конгрессе математиков
представил список из 23 нерешённых математических проблем. Эти проблемы охватили
множество областей математики и сформировали центр приложения усилий математиков XX столетия. Сегодня десять проблем из списка решены, семь частично решены, и две проблемы всё ещё открыты. Оставшиеся четыре сформулированы слишком обобщённо, чтобы имело смысл говорить об их решении.Особенное развитие в XX веке получили новые области математики; кроме компьютерных потребностей, это во многом связано с запросами теории управления, квантовой физики и других прикладных дисциплин.
Гильберт
Слайд 58Различные разделы дискретной математики.
Информатика и кибернетика.
Методы математической статистики.
Теория алгоритмов.
Теория графов.
Теория
групп Ли и других абстрактных структур.
Теория игр.
Теория информации.
Теория компьютерного моделирования.
Теория
оптимизации, в том числе глобальной.Теория случайных процессов.
Топология.
Функциональный анализ.
Слайд 59Бурно развивались и многие «старые» области математики.
Абстрактная алгебра
Алгебраическая геометрия
Комплексный анализ,
особенно для функций многих переменных
Математическая физика
Риманова геометрия
Теория вероятностей
Слайд 60Среди наиболее выдающихся математиков XX века можно назвать (помимо отдельно
упомянутых в данном разделе) такие имена:
Жак Адамар — теория чисел.
Павел Сергеевич
Александров— топология.Стефан Банах — функциональный анализ, теория множеств.
Лёйтзен Эгберт Ян Брауэр — анализ, топология, теория множеств, философия математики.
Герман Вейль — алгебра, анализ, теория чисел, математическая логика, математическая физика и др.
Норберт Винер — создатель кибернетики.
Израиль Моисеевич Гельфанд — функциональный анализ, топология, алгебра, группы Ли, математическая физика и др.
Жан Дьёдонне — функциональный анализ, группы Ли, топология, алгебраическая геометрия.
Анри Картан — анализ, топология.
Джон фон Нейман — математическая логика и теория компьютеров, математическая физика, теория множеств, информатика, экономика, теория игр и др.
Альфред Тарский — математическая логика.
Альфред Норт Уайтхед — математическая логика.
Феликс Хаусдорф — топология, теория множеств, функциональный анализ, теория чисел.
Александр Яковлевич Хинчин — теория вероятностей.
Алонзо Чёрч — информатика, математическая логика.
Клод Элвуд Шеннон — информатика, кибернетика.
Эрнст Цермело — математическая логика, теория множеств.
Слайд 61Список использованной литературы:
Глейзер Г. И. История математики в школе — М.:
Просвещение, 1964. — 376 с.
Ван дер Варден. Пробуждающаяся наука. Математика древнего
Египта, Вавилона и Греции — М.: Наука, 1959. — 456 с.http://dic.academic.ru
http://www.wikiznanie.ru