Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Измерение концентрации вещества в растворе 1. методом стандартов В методе
Содержание
- 1. Измерение концентрации вещества в растворе 1. методом стандартов В методе
- 2. Наиболее надежные результаты получают, когда в качестве
- 3. 2. Измерение концентрации вещества в растворе методом
- 4. При определении содержания компонента графическим методом берут
- 5. Слайд 5
- 6. Измерение концентрации вещества в растворе методом градуировочного
- 7. Выбор длины волныДля достижения наименьшей погрешности в
- 8. Спектр поглощения раствора синего фосфорномолибденового комплексаНа рис.
- 9. Спектры поглощения растворов сульфосалицилатных комплексов железа в
- 10. 45О 500 520, нм Калибровочный
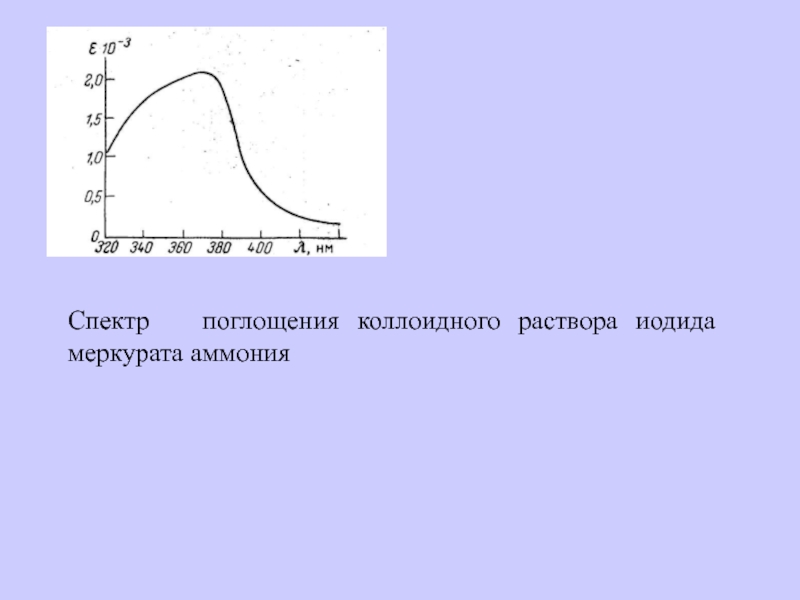
- 11. Спектр поглощения коллоидного раствора иодида меркурата аммония
- 12. Выбор кюветыПри определении концентрации вещества в растворе
- 13. В случае слабо окрашенных растворов работайте с
- 14. Построение градуировочного графика (линейный, или приводимый к
- 15. Подготовка градуировки – стр.8 ИСО 8466-1Сначала изучают
- 16. После установления предварительного рабочего диапазона определяются измеряемые
- 17. Далее определяют f-критерий расчетный, как отношение максимальной
- 18. Вычисление метрологических характеристик линейного графикаНаиболее объективным и
- 19. Если имеется п взаимосвязанных пар значений (уi
- 20. В левой части системы уравнении находятся измеренные
- 21. Следовательно, задача линейного регрессионного анализа (метода наименьших
- 22. Вычисление метрологических характеристик результатов анализаПосле того как
- 23. Для градуировочной зависимости вычисляют величину коэффициента корреляции
- 24. Для оценки погрешности в регрессионном анализе вводится
- 25. Остаточная дисперсия позволяет оценить адекватность градуировочной модели.
- 26. 2) означает, что модель "слишком хорошая", перепараметризация.
- 27. Далее необходимо оценить погрешность коэффициентов модели. Поскольку
- 28. В данном случае это условие выполняется (это
- 29. Рассчитывают дисперсию, характеризующую рассеяние по хSxx =
- 30. Следующий шаг:Необходимо проверить полученную градуировочную зависимость на
- 31. Если полученное по этому соотношению значение критерия
- 32. Нарушение линейности обусловливается различными причинами. Так, при
- 33. Следующий этап:Расчет стандартного отклонения результата анализа(стр. 316
- 34. 2. Чем больше число точек в градуировочном
- 35. Проверка однородности дисперсий по критерию Кохрена (G).наибольшая
- 36. 2. Предел обнаружения CminПредел обнаружения Cmin -
- 37. Предел обнаруженияРанее указывалось, что предел обнаружения определяется
- 38. Фоновый сигнал не подчиняется нормальному распределению. Он
- 39. Слайд 39
- 40. Слайд 40
- 41. 3. Нижняя граница определяемых содержаний СнНижняя граница
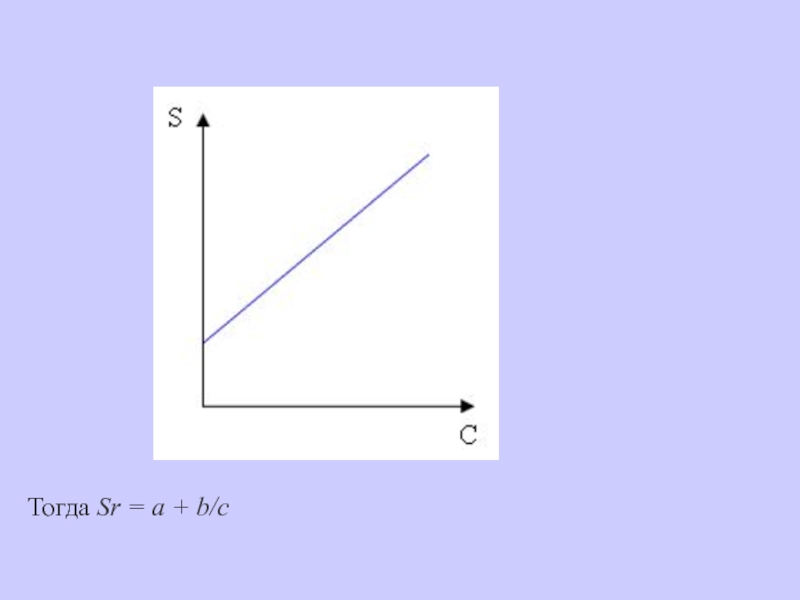
- 42. Тогда Sr = a + b/c
- 43. Чтобы определить Сн, готовят ряд образцов с
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Доверительный интервал результата анализа Δхан = S
- 49. Уравнение параболической зависимости:Булатов, Калинкин, стр. 323
- 50. Виды преобразований для получения линейной зависимостиI – измеряемый сигнал, А – концентрация СО
- 51. Контроль стабильности градуировочных характеристик заключается в определении
- 52. Градуировочную характеристику считают стабильной при выполнении для
- 53. Если градуировочная характеристика нестабильна, делают вывод о
- 54. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Наиболее надежные результаты получают, когда в качестве образцов сравнения используют
стандартные образцы — специально приготовленные материалы, состав и свойства которых достоверно установлены
и официально аттестованы специальными государственными метрологическими учреждениями.В способе ограничивающих растворов линейный (в выбранном концентрационном диапазоне) характер градуировочной функции постулируют заранее (и, при возможности, экспериментально проверяют), а стандартный раствор выбирают так, чтобы С1<Сx
Слайд 32. Измерение концентрации вещества в растворе методом добавок
Если нужно
учесть влияние матрицы образца, часто используют метод добавок — расчетный и графический.
При
определении содержания расчетным методом берут две аликвоты раствора анализируемой пробы. В одну из них вводят добавку определяемого компонента известного содержания. В обеих пробах измеряют аналитический сигнал — ух и ух+доб. Неизвестную концентрацию определяемого компонента рассчитывают по формуле:где Vдоб и Сдоб — объем и концентрация добавленного раствора определяемого компонента; V — аликвота анализируемой пробы.
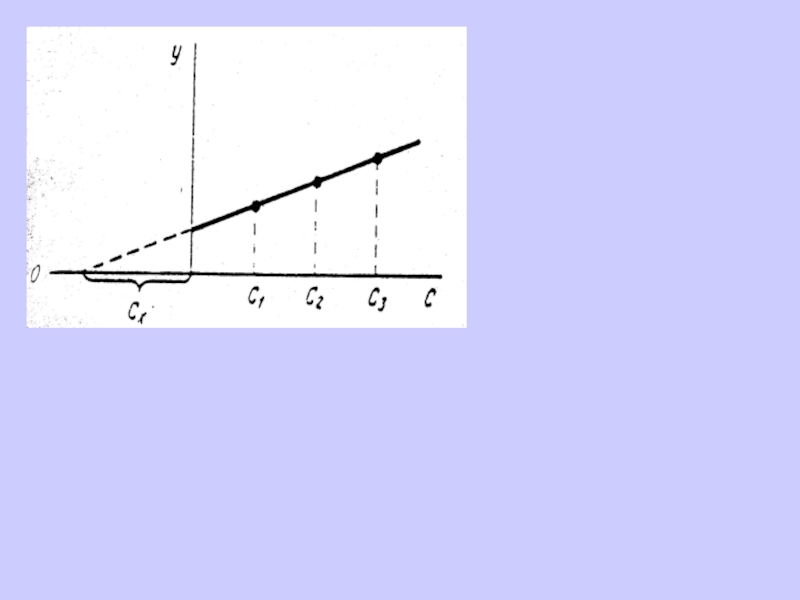
Слайд 4При определении содержания компонента графическим методом берут n аликвот анализируемой
пробы: 1, 2, 3, , n. В аликвоты 2, 3,,
n вводят известные, возрастающие количества определяемого компонента. Во всех аликвотах измеряют аналитический сигнал и строят график в координатах аналитический сигнал — содержание определяемого компонента, приняв за условный ноль содержание определяемого компонента в аликвоте без добавки (аликвота 1). Экстраполяция полученной прямой до пересечения с осью абсцисс дает отрезок, расположенный слева от условного нуля координат, величина которого в выбранном масштабе и единицах измерения соответствует искомому содержанию (Cх) определяемого компонентаСлайд 6Измерение концентрации вещества в растворе методом градуировочного графика
Для измерения
концентрации вещества в растворе необходимо предварительно выполнить ряд подготовительных операций
в следующей последовательности:выбор длины волны;
выбор кюветы;
построение градуировочного графика для данного вещества;
измерение концентрация вещества.
Слайд 7Выбор длины волны
Для достижения наименьшей погрешности в определении концентрации следует
правильно выбрать длину волны, на которой будет выполняться измерение. Для
этого по спектральной кривой раствора, выбрать такой участок, на котором выполняются следующие условия:- оптическая плотность имеет максимальную величину;
- ход кривой примерно параллелен горизонтальной оси
т. е. оптическая плотность мало зависит от длины волны.
Длина волны, соответствующая этому участку, выбирается для измерения. Если для некоторых растворов второе условие не выполняется, то рабочая длина волны выбирается по первому условию
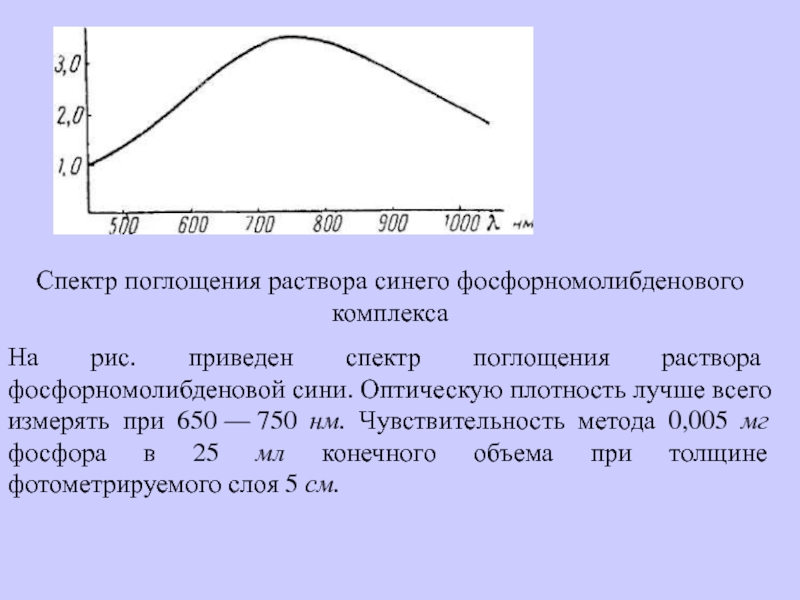
Слайд 8Спектр поглощения раствора синего фосфорномолибденового комплекса
На рис. приведен спектр поглощения
раствора фосфорномолибденовой сини. Оптическую плотность лучше всего измерять при 650 — 750
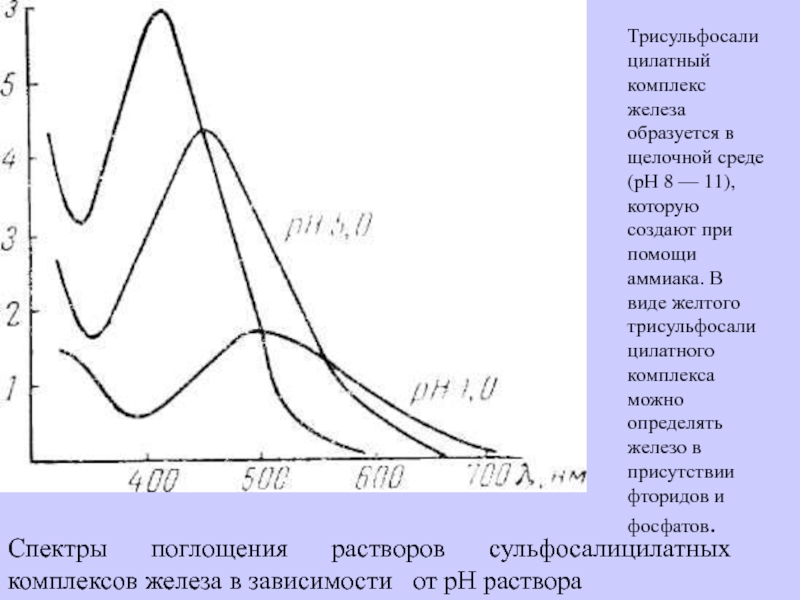
нм. Чувствительность метода 0,005 мг фосфора в 25 мл конечного объема при толщине фотометрируемого слоя 5 см.Слайд 9Спектры поглощения растворов сульфосалицилатных комплексов железа в зависимости от
рН раствора
Трисульфосалицилатный комплекс железа образуется в щелочной среде (рН 8 — 11),
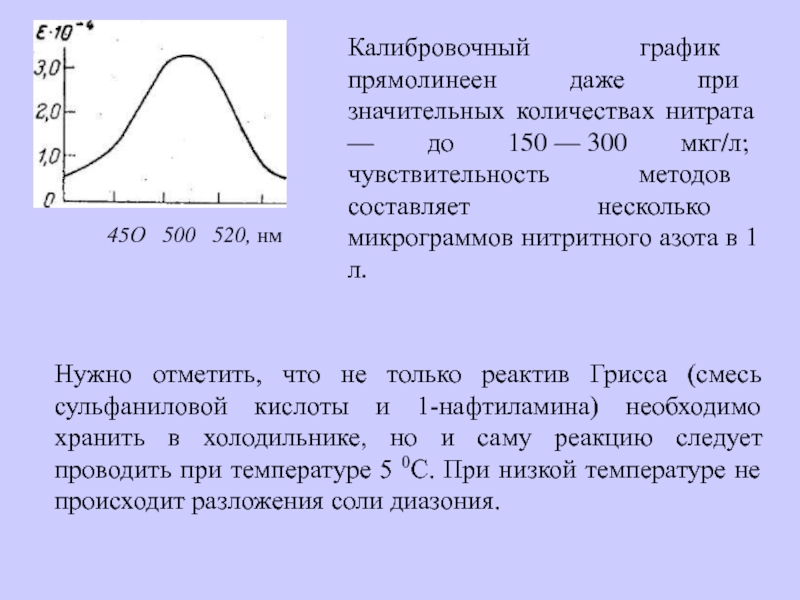
которую создают при помощи аммиака. В виде желтого трисульфосалицилатного комплекса можно определять железо в присутствии фторидов и фосфатов. Слайд 1045О 500 520, нм
Калибровочный график прямолинеен даже
при значительных количествах нитрата — до 150 — 300 мкг/л; чувствительность методов
составляет несколько микрограммов нитритного азота в 1 л.Нужно отметить, что не только реактив Грисса (смесь сульфаниловой кислоты и 1-нафтиламина) необходимо хранить в холодильнике, но и саму реакцию следует проводить при температуре 5 0С. При низкой температуре не происходит разложения соли диазония.
Слайд 12Выбор кюветы
При определении концентрации вещества в растворе необходимо сделать правильный
выбор кюветы. Абсолютная погрешность измерения коэффициента пропускания не превышает 0,5%.
Относительная погрешность измерения оптической плотности раствора будет различной и достигает минимума при значении оптической плотности 0,4.Поэтому при работе на фотометре рекомендуется путем соответствующего выбора длины кювет работать вблизи указанного значения оптической плотности, например, в пределах от 0,2 до 0,8. При работе на приборе работайте вблизи указанного значения оптической плотности.
Если раствор интенсивно окрашен (темный), пользуйтесь кюветами с малой рабочей длиной (10 мм).
Слайд 13В случае слабо окрашенных растворов работайте с кюветами с большей
рабочей длиной (50 мм).
В предварительно подобранную кювету налейте раствор
и измерьте его оптическую плотность, введя в ход лучей соответствующий для данного раствора светофильтр. При измерении ряда растворов кювету заполните раствором средней концентрации.Если полученное значение оптической плотности составляет примерно 0,2—0,8, то данную кювету выбирайте для работы с этим раствором. В том случае, когда это не выполняется, испробуйте кювету другой рабочей длины.
Слайд 14Построение градуировочного графика (линейный, или приводимый к линейному)
Построение градуировочного графика
проводить следующим образом. Приготовить ряд растворов данного вещества с известными
концентрациями, охватывающими область возможных изменений концентраций этого вещества в исследуемом растворе.Измерить оптические плотности всех растворов и построить градуировочный график, откладывая по горизонтальной оси известные концентрации, а по вертикальной — соответствующие им значения оптической плотности, рассчитанные по методу наименьших квадратов.
Слайд 15Подготовка градуировки – стр.8 ИСО 8466-1
Сначала изучают объект исследования, определяют
диапазон содержания определяемого компонента
Cmax и Сmin
После этого определяют диапазон градуировки,
так, чтобы Сmax гр. = 1,1 Cmax
Cmin гр. = 0,5 Сmin
Слайд 16После установления предварительного рабочего диапазона определяются измеряемые значения для не
менее 5 (рекомендуемое значение 10) стандартных образцов.
Концентрация хi данных
стандартных образцов равномерно распределяется по рабочему диапазону. Для того, чтобы определить равномерность рассеяния, нужно рассчитать десять повторов (5) Сmax гр и Cmin гр рабочего диапазона. Получают соответственное количество данных аналитического сигнала.Рассчитывают
Si 2 = Σ(yi,j – yi ср.)2/(n – 1)
Слайд 17Далее определяют f-критерий расчетный, как отношение максимальной дисперсии к ми
нимальной из двух рассчитанных:
Fрасч = Smax 2 / Smin 2
если Fрасч < Fтабл, то разница между дисперсиями несущественна
если Fрасч > Fтабл., то разница между дисперсиями значительна. В этом случае рабочий диапазон должен быть уменьшен.
Слайд 18Вычисление метрологических характеристик линейного графика
Наиболее объективным и правильным является установление
математической зависимости А = f (С), которую находят методом регрессионного
анализа. В фотометрических методах она выражается обычно линейной и, значительно реже, параболической зависимостью.Вычисление параметров а и b. В общем случае линейная зависимость выражается уравнением:
у = а + bх
Значения параметров а и b вычисляют методом регрессионного анализа. Величина a, представляющая собой значение аналитического сигнала при нулевой концентрации определяемого компонента, называется фоновым значением сигнала. Она играет важную роль при оценке чувствительности методик
Слайд 19Если имеется п взаимосвязанных пар значений (уi хi), то можно
записать:
Здесь n — число измерений;
хi, — известное содержание
(концентрация) определяемого компонента в i-м стандартном растворе; уi — результат измерении аналитического сигнала (оптической плотности) i-го стандартного раствора.
Слайд 20В левой части системы уравнении находятся измеренные значения уi, а
в правой — вычисленные значения Yi = а + bхi.
Разность между обеими величинами дает погрешность. Аналитически задача метода наименьших квадратов может быть выражена в следующей форме:SQ = (yi – Yi)2 = ( yi – (a + bxi)2мин
Если yi – (a + bxi) = δi, тогда
SQ = δi2, i = 1, …, n
Слайд 21Следовательно, задача линейного регрессионного анализа (метода наименьших квадратов) состоит в
том, чтобы сумма квадратов отклонений SQ экспериментальных точек (уi хi)
вдоль ординаты от проведенной прямой была минимальной.Для того, чтобы найти параметры а и b, удовлетворяющие минимуму SQ, берут частные производные относительно а, затем относительно b, полученные выражения приравнивают нулю и, решая уравнения, находят;
а= (yi - b xi)/n
Слайд 22Вычисление метрологических характеристик результатов анализа
После того как определена функциональная зависимость
у = а + bх и рассчитаны значения а, b,
Δа, Δb, по данным измерений аналитического сигнала у (оптическая плотность A) анализируемых проб рассчитывают метрологические характеристики результата анализа.Слайд 23Для градуировочной зависимости вычисляют величину коэффициента корреляции (r)
r = (XY
- X * Y)/( s x * s y ).
s x и s y – среднеквадратические отклонения
Слайд 24Для оценки погрешности в регрессионном анализе вводится понятие дисперсии адекватности
(или остаточной дисперсии). Это дисперсия относительно регрессионной модели:
где y -
экспериментальное значение аналитического сигнала, Y - рассчитаное по уравнению градуировки значение аналитического сигнала, n - число измерений, k - число параметров модели (для линейной градуировки k=2)Нетрудно заметить, что при построении градуировки методом МНК дисперсия адекватности будет минимальной
Слайд 25Остаточная дисперсия позволяет оценить адекватность градуировочной модели. Для этого необходимо
сравнить дисперсию адекватности и дисперсию воспроизводимости (дисперсию аналитического сигнала для
одного образца при серии параллельных измерений) по критерию Фишера:Возможны три случая:
1)
- говорит о том, что выбранная модель плохая. Нужно больше параметров.
Слайд 262)
означает, что модель "слишком хорошая", перепараметризация. Нужно уменьшить число
параметров, т.к. модель описывает еще и погрешность
3) Различие незначимо
- хорошая модель. Если существует несколько хороших моделей, выбирают самую простую. При этом можно усреднить дисперсию адекватности и дисперсию воспроизводимости (с учетом числа степеней свободы) и получить общую дисперсию S2(y), которая будет служить оценкой случайной погрешности модели.
Слайд 27Далее необходимо оценить погрешность коэффициентов модели. Поскольку они расчитываются линейным
преобразованием, то они подчиняются нормальному закону распределения. Для расчета соответствующей
дисперсии необходимо воспользоваться законом распространения погрешности:если f = f(x1, x2 ... xn), то - при условии, что аргументы xi не коррелируют между собой
Слайд 28В данном случае это условие выполняется (это одна из предпосылок
МНК), поэтому, применив закон распространения погрешности к формулам для коэффициентов
линейной модели a и b, получим следующие выражения:Слайд 29Рассчитывают дисперсию, характеризующую рассеяние по х
Sxx = Σxi2 – (Σxi)2/n
Далее рассчитывают t-критерий по коэффициенту регрессии а:
tа = Sxx/Sa
Если t-отношение
больше табличного критерия Стьюдента (при Р=0,95 и степенях свободы f=n-1) коэффициент а значим.Если обратное соотношение, то коэффициент а убираем из расчетной зависимости
Слайд 30Следующий шаг:
Необходимо проверить полученную градуировочную зависимость на линенйность по критерию
Фишера.
Для этого рассчитывают дисперсию, характеризующую рассеяние результатов относительно прямой
Syx =
k*(Σ(yi – Yi)2)/(n-2)Sxу = Σ(xi*yi) – (Σxi * ΣYi)/n
Рассчитывают дисперсию, характеризующую рассеяние по у
Sy = (Σ(yср–y i)2)/(n(k-1))
После этого рассчитываю f-критерий: f = Syx/ Sy
F = Дисперсия разброса средних значений/ дисперсия разброса внутри параллельных значений
И сравнивают с табличным значением критерия Фишера при Р = 0,95 и степенях свободы f1 = n-2
f2= = n(k-1)
Слайд 31Если полученное по этому соотношению значение критерия Фишера не превышает
табличной величины (F табл.)при данном числе степеней свободы, уравнение регрессии
является адекватным.Если полученное по этому соотношению значение критерия Фишера не превышает табличной величины (F табл.)при данном числе степеней свободы, уравнение регрессии является адекватным.
Слайд 32Нарушение линейности обусловливается различными причинами. Так, при фотоколориметрических определениях линейная
зависимость между оптической плотностью растворов и концентрацией определяемого компонента в
ряде случаев не выполняется. Эти отклонения бывают обусловлены рядом причин, связанных с состоянием вещества в растворе, а чаще с недостаточной монохроматичностью светового потока при использовании фотоколориметров с относительно широкими полосами пропускания света.Слайд 33Следующий этап:
Расчет стандартного отклонения результата анализа
(стр. 316 – Булатов, Калинкин)
Анализ
этого уравнения показывает, что эта дисперсия тем меньше, чем
1. Круче
градуировочный график, т.е. чем больше коэффициент экстинкции и больше толщина кюветы.Слайд 342. Чем больше число точек в градуировочном графике. В общем
случае оно должно быть не менее 5.
3. Чем меньше
разность между рассчитанным и экспериментально определенным значением у. Эта разница тем меньше, чем менее растянут градуировочный график.Слайд 35Проверка однородности дисперсий по критерию Кохрена (G).
наибольшая из дисперсий, рассчитанных
как
Критерий Кохрена вычисленный должен быть меньше табличного.
d - отклонение от
среднего (м.б х-хср.k – число серий
Число степеней свободы f = k - 1
Слайд 362. Предел обнаружения Cmin
Предел обнаружения Cmin - содержание, которое можно
обнаружить с заданной достоверностью. Необходимо "увидеть" сигнал определяемого вещества на
фоне шумов, т.е. выяснить, значимо ли различие между сигналом фона и сигналом определяемого компонента.Слайд 37Предел обнаружения
Ранее указывалось, что предел обнаружения определяется значением холостого опыта
и его случайными отклонениями. Имея уравнение регрессии, также можно экстраполировать
значение у при х =0, т.е.У мин = а + t* Sa
Х мин = t *(Sa + х ср.*Sb)/(b + t*Sb)
чувствительность
Слайд 38Фоновый сигнал не подчиняется нормальному распределению. Он обычно принимается равным
3S0
где S0 - дисперсия фонового сигнала, k - угловой коэффициент
градуировочной прямойПоскольку мат.ожидание для фонового раствора есть абсолютная неизвестная величина (кроме того, считается для генеральной совокупности) , считаем, что это средняя величина С фона
Слайд 413. Нижняя граница определяемых содержаний Сн
Нижняя граница определяемых содержаний Cн
- содержание, которое можно определить с заданной точностью.
Всегда выполняется Сmin
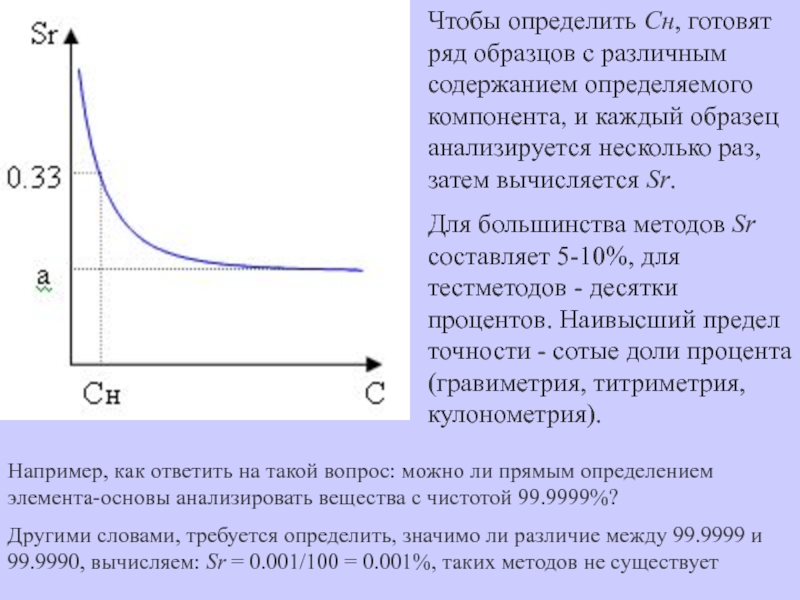
< CнПринимается, что Сн соответствует таким содержаниям, относительное стандартное отклонение определения которых Sr = 0.33
Рассмотрим зависимость стандартного отклонения от определяемой концентрации. В общем виде это линейно возрастающая функция S = ac + b, причем b > 0
Слайд 43Чтобы определить Сн, готовят ряд образцов с различным содержанием определяемого
компонента, и каждый образец анализируется несколько раз, затем вычисляется Sr.
Для
большинства методов Sr составляет 5-10%, для тестметодов - десятки процентов. Наивысший предел точности - сотые доли процента (гравиметрия, титриметрия, кулонометрия).Например, как ответить на такой вопрос: можно ли прямым определением элемента-основы анализировать вещества с чистотой 99.9999%?
Другими словами, требуется определить, значимо ли различие между 99.9999 и 99.9990, вычисляем: Sr = 0.001/100 = 0.001%, таких методов не существует
Слайд 48Доверительный интервал результата анализа
Δхан = S ан *t
При f
= n-2Тогда границы доверительного интервала результата анализа находят как
Хан +
Δхан Слайд 50Виды преобразований для получения линейной зависимости
I – измеряемый сигнал, А
– концентрация СО
Слайд 51Контроль стабильности градуировочных характеристик заключается в определении параметров градуировочного графика
через установленные промежутки времени, сопоставлении их с первоначальными параметрами и
установлении на этой основе возможности продолжения текущих измерений или необходимости коррекции градуировочной характеристики.Контроль стабильности градуировочной характеристики проводят при смене основных реактивов, но не реже одного раза в квартал.
При контроле стабильности градуировочной характеристики проводят измерение не менее трех образцов для градуировки, содержания измеряемого компонента в которых должны охватывать весь диапазон МВИ. Полученные результаты сравнивают с соответствующими точками первоначальной градуировочной характеристики.
Слайд 52Градуировочную характеристику считают стабильной при выполнении для каждого образца одного
из следующих условий (с учетом вида градуировочной характеристики):
Здесь у -
измеряемое содержание определяемого компонента, соответствующее значению выходного сигнала ; х - результат контрольного измерения, соответствующий значению выходного сигнала контр; a, b - постоянные коэффициенты градуировочной характеристики; ( ) - значение показателя воспроизводимости измерений, соответствующее содержанию С измеряемого компонента в образце для градуировки.Слайд 53Если градуировочная характеристика нестабильна, делают вывод о невозможности применения измерительной
установки для дальнейших измерений. В этом случае выясняют и устраняют
причины нестабильности градуировочной характеристики и повторяют контроль ее стабильности с использованием других образцов для градуировки, предусмотренных МВИ. При повторном обнаружении нестабильности градуировочной характеристики строят новый градуировочный график.Дату проведения и результаты контроля стабильности градуировочной характеристики заносят в журнал «Внутренний контроль точности».