Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Измерение скорости полёта пули
Содержание
- 1. Измерение скорости полёта пули
- 2. Актуальность
- 3. Первоначально я предположила, что в нашем мире
- 4. Слайд 4
- 5. Слайд 5
- 6. Параболический методКриволинейное баллистическое движение тела можно рассматривать
- 7. Эксперимент Расстояние от ружья до цели –
- 8. Баллистический маятникБаллистический маятник представляет собой тяжёлое тело
- 9. Баллистический МаятникЗакон сохранения импульса: m1*V=(M+m1)U
- 10. Баллистический МаятникДлина подвеса 200 см от оси
- 11. Баллистический МаятникПо теореме Пифагора: ОА=
- 12. Измерение скорости пули методом ШтернаВ 1920 г.
- 13. Измерение скорости пули методом ШтернаВ качестве конструкции
- 14. Опыт по методу ШтернаРасстояние между дисками
- 15. Опыт по методу ШтернаОтклонение L
- 16. Опыт по методу ШтернаТеперь найдём скорость пули
- 17. Хронограф - прибор для измерения скорости пули.Электронное
- 18. Хронограф1 выстрел=142 м/с2 выстрел=144 м/с3 выстрел=144 м/с142+144+144=430
- 19. Анализ экспериментов.
- 20. ЗаключениеВ начале проекта я выдвинула гипотезу о
- 21. Спасибо за внимание!!!
- 22. Скачать презентанцию
Актуальность
Слайды и текст этой презентации
Слайд 1Министерство общего и профессионального образования
Свердловской области
Муниципальное автономное общеобразовательное учреждение
«Верхнедубровская средняя
общеобразовательная школа»
Слайд 3Первоначально я предположила, что в нашем мире существует какой-нибудь физический
способ для определения скорости полета пули и его можно осуществить
на практике.Слайд 6Параболический метод
Криволинейное баллистическое движение тела можно рассматривать как результат сложения
двух прямолинейных движений: равномерного движения по горизонтали и равнопеременного движения
по вертикали под действием силы тяжести.х
Слайд 7Эксперимент
Расстояние от ружья до цели – S=386 cм.
Смещение по вертикали
Х от места попадания пули до выбранной цели оказалось 3мм
или 0,003м.Тогда время падения пули t =√(2x/g) = √((2*0,003)/9,8)=0,025c.
Тогда скорость пули можно определить:
V= S/t=(3,86 м )/(0,025 с ) = 154,4 м/с
Слайд 8Баллистический маятник
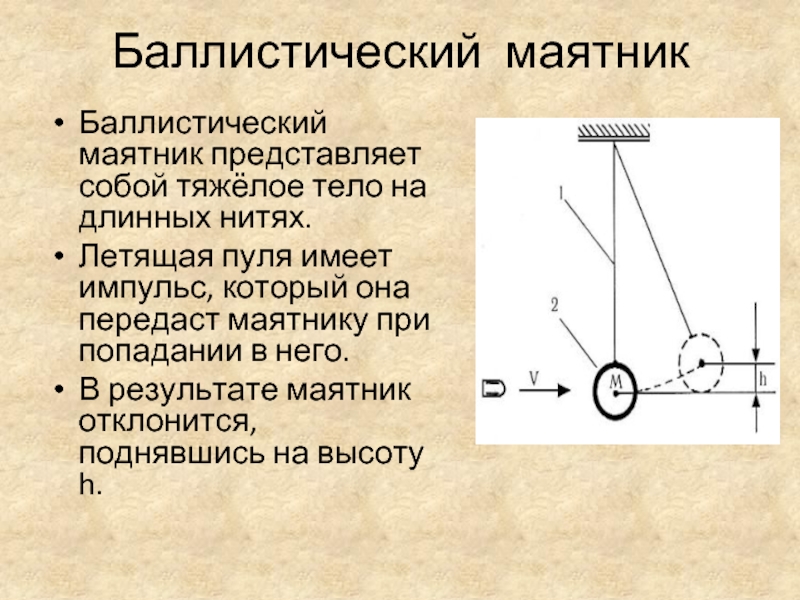
Баллистический маятник представляет собой тяжёлое тело на длинных нитях.
Летящая
пуля имеет импульс, который она передаст маятнику при попадании в
него.В результате маятник отклонится, поднявшись на высоту h.
Слайд 9Баллистический Маятник
Закон сохранения импульса:
m1*V=(M+m1)U ,
где m1V- импульс пули,
(M+m1)U- импульс
маятника после выстрела.Закон сохранения энергии
Ек=Ер
((M+m1 )*U^2)/2 = (M+m1)hg
U2/2=hg
Слайд 10Баллистический Маятник
Длина подвеса 200 см от оси подвеса до середины
бруска
m10 пуль=6,88 г
m1 пули=0,688 г
Расстояние до маятника=1,5 м
Отклонение маятника 14
смMмаятника=200,38 г
M в эксперименте=Mмаятника+m1пули =201,068г
Слайд 11Баллистический Маятник
По теореме Пифагора:
ОА= √(22-x2 )=√(4-0,142)=√3,98 =1,99
м
Тогда высота подъема маятника:
h=2м-ОА=2-1,99 =0,01м=1см
Скорость
маятника: U=√2gh=√(2*9,8*0,01)=√0,0298 = 17 м/сСкорость пули:
V=((M+m1)*U)/m1 = ((201,068+0,688)*0,17)/0,688 = 49,9 м/с
А
О
В
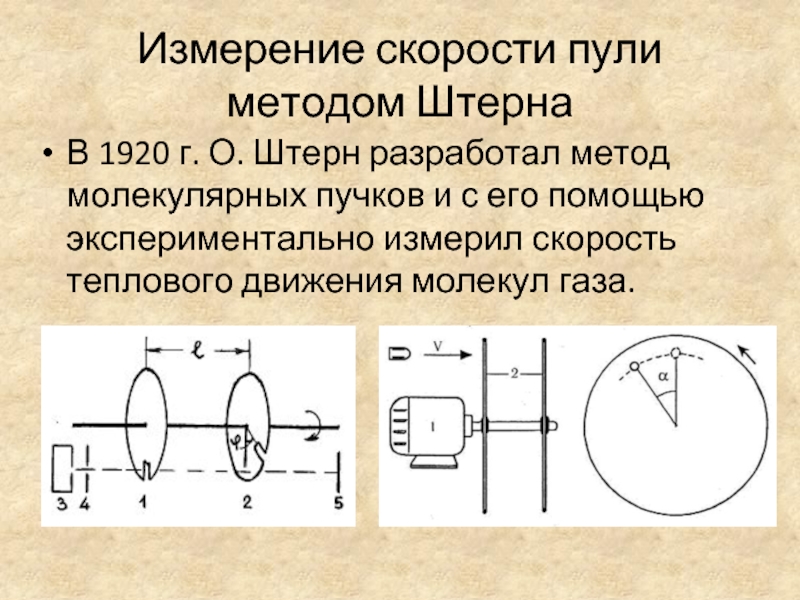
Слайд 12Измерение скорости пули методом Штерна
В 1920 г. О. Штерн разработал
метод молекулярных пучков и с его помощью экспериментально измерил скорость
теплового движения молекул газа.Слайд 13Измерение скорости пули методом Штерна
В качестве конструкции механической установки Штерна
используем два диска, закрепленных на одной вращающейся оси проигрывателя пластинок.
Слайд 14Опыт по методу Штерна
Расстояние между дисками
h=10,5 см=0,105 м.
Радиус картонных дисков составил:
R=10 см=0,1 м.Проигрыватель произвел 5 оборотов за 8,27 с
Отсюда время одного оборота Т=1,654 с.
Слайд 15Опыт по методу Штерна
Отклонение
L = 3
мм =0,003 м
Применяем формулу длины окружности –
2πR = 2*3,14*0,1.Для определения времени Х пролета пули воспользуемся пропорцией:
Т /х = 2πR/L
1,654/х = ( 2*3,14*0,1)/0,003,
Отсюда время полета пули между двумя дисками
х=(1,654*0,003)/(2*3,14*0,1)=0,008 с.
Слайд 16Опыт по методу Штерна
Теперь найдём скорость пули :
V=S/t
V=(0,105 м)/(0,008 с)=13,125 м/с
Погрешность этого эксперимента составляет:
V/(Vст.)*100= 13,125/144*100=9%Слайд 17Хронограф - прибор для измерения скорости пули.
Электронное устройство, которое имеет
максимально малую погрешность.
Любой способ непосредственного измерения величины имеет малую
погрешность.Кроме того прибор позволяет определить непосредственно скорость пули при выстреле – начальную скорость пули.
Слайд 18Хронограф
1 выстрел=142 м/с
2 выстрел=144 м/с
3 выстрел=144 м/с
142+144+144=430 м/с – сумма
значений скорости пули трех выстрелов
(430 м/с)/3 =143.3м/с – среднее значение.
Слайд 20Заключение
В начале проекта я выдвинула гипотезу о том, что существует
физический способ определения скорости полета пули.
Моя гипотеза подтвердилась. Действительно,
есть такие способы и при том не один.Школьная физика далека от реальности!
Теги