Слайд 1Качественные и количественные методы психологических и педагогических исследований
Слайд 2Введение в раздел
«Качественные и количественные методы психолого-педагогических исследований»
Учебная дисциплина направлена
на систематизацию знаний о процедурных особенностях качественных и количественных методах,
а также практическом применении конкретных методов и техник в практике исследовательской деятельности.
Качественные и количественные методы – это инструменты работы с массивами данных, их фиксации и анализа разного уровня.
Слайд 3Введение в предмет курса
«Качественные и количественные методы психолого-педагогических исследований»
Качественные
методы
(сбор качественных данных с последующем применением техник и приёмов
извлечение смысла)
Количественные методы
(сбор числовых данных с последующим статистическим анализом данных)
Методы фиксации:
Запись интервью.
Рисуночные методики.
Дневниковые записи.
Фиксация аудио- и видеоматериалов
Методы анализа:
Качественный контент-анализ.
Феноменологический анализ.
Дискурс-анализ.
Нарративный анализ.
Методы фиксации:
Методы измерения психологических переменных.
Приёмы квантификация качественного материала.
Методы анализа:
Методы описательной статистики.
Методы статистического вывода.
.
Слайд 4Введение в предмет курса
«Качественные и количественные методы психолого-педагогических исследований»
Количественный
анализ предполагает прирост научной информации за счёт вдумчивого и всестороннего
анализа количественной информации (основа - прочная методологическая позиция исследователя, сформированная на основе теоретического анализа проблемы исследования).
Количественные данные выражаются числами.
Качественный анализ позволяет выяснить причины явления; установить взаимосвязи между объектом и предметом исследования; вскрыть сущность явления: сделать обобщающие выводы.
Качественные данные соотносятся с языковыми единицами (словами, фразами, текстом, рисунками.) и не предполагает использование статистических процедур.
Слайд 5
Описание данных – этап анализа данных, в ходе реализации которого
данные приводятся к виду доступному для различных теоретических процедур, позволяющих
раскрыть сущность явлений или выявленных взаимосвязей.
Описывая эмпирические данные, исследователь придаёт им экономную, строгую (стандартную) форму и наглядность (построение рядов распределения (диаграмм, гистограмм), расчёт среднего арифметического значения и дисперсий и т.п.
Слайд 6Объяснение (интерпретация) данных – позволяет раскрыть сущность объекта на основе
анализа эмпирических данных и теоретических положений.
Объяснение предполагает выдвижение, обоснование
и проверку гипотез с использованием статистических методов (статистических критериев) установления взаимосвязей, различий, динамики и т. п.
Слайд 7Признаками или переменными - измеряемые в ходе эксперимента психологические явления.
Данные – это информация, относящаяся к предмету исследования,
направленная на решение его задач. На этапах исследования данные проходят обработку и обобщение разного уровня.
Массив данных - упорядоченная совокупность однородных по структуре и способу получения показателей.
Обработка данных – это преобразование эмпирических данных в тот вид, который необходим для решения поставленных в исследовании задач.
Слайд 8Порядок обработки качественных и количественных данных
Качественные данные
Количественные данные
Качественный анализ
Перевод качественного
материала в числовые категории
Количественный анализ
Интерпретация результатов количественного анализа
Слайд 9Первичный математический анализ связан с применением стандартных методов описания представления
данных (таблично-графических и связанных с вычислением первичных статистических параметров).
Вторичный анализ
предполагает использование критериев, позволяющие с заданной степенью вероятности принять истинную статистическую гипотезу и отклонить ложную.
Например, при необходимости определить взаимосвязь переменных основой реализации такой задачи станет корреляционного анализ данных).
Слайд 10
Количественная информация может быть представлена:
абсолютными величинами как результат подсчёта
общего числа единиц определённой совокупности
относительными величинами (например, частотность или
расчёт процентов).
Параметры распределения – это числовые характеристики, указывающие на то, где в «среднем» располагается значение признака.
Параметр – это оценка или значение, полученное в результате применения различных описательных мер, например, расчет среднего арифметического значения, стандартного отклонения, моды, частоты и др.
Слайд 11Параметры распределения результативного признака
Выделяют две группы мер (способов оценивания значений
параметра):
меры положения (центральных тенденций): мода, медиана, среднее арифметическое значение
(и другие средние величины, например, среднее гармоническое, кубическое и др.).
меры изменчивости признака: вариационный размах, коэффициент вариации, дисперсия, среднее квадратичное отклонение, асимметрия, эксцесс.
Слайд 12Параметры распределения признаков: меры положения
Медиана для нечётного ряда определяется по
формуле:
Медиана – значение признака, находящееся в середине ряда
и делящее его пополам.
В результате половина единиц совокупности лежит ниже, а половина выше медианы.
;
Например; 4, 5, 5, 6, 7, 7, 8. n = 7;
т.е. медиана – 4-е значение упорядоченного ряда. В чётных рядах медиана лежит между двумя значениями упорядоченного ряда.
Например; 5, 5, 8, 9, 11, 11. n = 6;
Медиана лежит между 3-им и 4-ым значение упорядоченного ряда.
Слайд 13Параметры распределения признаков : меры положения.
Мода – наиболее часто встречаемое
значение ряда.
Если все значения встречаются одинаково часто, то выборка не
имеет моды. В этом случае выборка называется унимодальной.
Например; 5, 5, 7, 7, 8, 8, 9, 9. Мо = 0.
Когда два соседних значения имеют одинаковую частоту, и они не больше частоты любого другого значения по выборке, то мода есть среднее этих двух значений.
Например, 1, 1, 2, 2, 2, 3, 3, 3, 4. Мо = 2,5.
Если два несмежных значения имеют одинаковую частоту, то будет две моды. В этом случае выборка называется бимодальной.
Например; 11, 12, 12, 12, 13, 14, 14, 14, 15. Мо = 12 и 14.
Слайд 14Параметры распределения признаков : меры положения.
Определяется по формуле:
Где -
каждое наблюдаемое значение признака;
i – указывает на порядковый номер данного
значения признака;
n – количество наблюдений;
Σ – сумма.
Среднее арифметическое значение (выборочная средняя) – среднее значение признака по группе с учётом её численности.
Слайд 15Параметры распределения признаков: меры изменчивости признака.
Вариационный размах (размах показателей) –
количественная мера, характеризующая разность между максимальным и минимальным значениями признака
по группе. Даёт информацию о совокупности тестовых оценок, но является самой грубой формой анализа.
Определяется по формуле: d = Хмах – Хmin;
Например; 4, 5, 5, 6, 7, 7, 8; d = 8 – 4 = 4;
Слайд 16Параметры распределения признаков: меры изменчивости признака.
Определяется по формуле:
Коэффициент вариации (коэффициент вариативности) – выраженное в процентах отношение стандартного
отклонения к среднему арифметическому значению. Мера, позволяющая сделать выводы об однородности показателей по выборке.
Если CV < 33%, то выборка однородна, то есть не имеет слишком большого разброса показателей относительно среднего значения.
Слайд 17Параметры распределения признаков: меры изменчивости признака.
Среднее квадратичное отклонение (стандартное
отклонение, сигма) – показывает, насколько в среднем отклоняется каждая варианта
от среднего арифметического значения. Чем сильнее разброс вариант, тем больше σ.
σ =
Дисперсия:
Слайд 18Параметры распределения признаков: меры изменчивости признака.
Асимметрия – количественная мера «скошенности»
симметричного распределения. Показывает плавность или крутость боковой части кривой. При
симметричных распределениях А=0 чем больше отклонение от нуля, тем больше показатель асимметрии.
«Скошенные» распределения бывают отрицательными (А<0) и положительными (А>0), правосторонними ( М>Ме>Мо) и левосторонними (М <Ме<Мо, т.е. наименьшим является значение среднего арифметического значения, а наибольшим Мо).
Слайд 19Параметры распределения признаков: меры изменчивости признака.
Слайд 20Параметры распределения признаков: меры изменчивости признака.
Определяется по формуле:
Где - каждое наблюдаемое значение признака;
-
среднее арифметическое;
n – количество наблюдений;
Σ – сумма;
σ – стандартное отклонение.
Слайд 21Параметры распределения признаков: меры изменчивости признака
Эксцесс – показатель островершинности («горбатости»)
распределения. Островершинные (эксцессивные) распределения, более высокие в средней части, характеризуются
положительным эксцессом (Е>0). При уменьшении показателя (Е<0) кривая становится плоской или «седловидной». При нормальном распределении Е=0.
Слайд 22Параметры распределения признаков: меры изменчивости признака.
Определяется по формуле:
Показатель эксцесса лежит в интервале: -3 < Е < +∞.
Слайд 23Выборка неоднородная (CV= 39.6%), распределение унимодальное с размахом показателей –
26 единиц. Распределение положительное, левостороннее (А=0,28), с отрицательным эксцессом (Е=
-1,76), со средним значением = 25,7, стандартным отклонением = 10,18.
Слайд 24Табличные формы представления материала
Процесс составления таблиц называется табулированием и
является следствием группировки данных.
Строки – это объект изучения, числовые данные
или др. значения показателей, которые рассматриваются исследователем. В одной строке располагаются данные, полученные одним испытуемым, например, по всем методикам.
Столбцы (графы) таблицы – это систематические показатели, значения одного признака по всей выборке (всем испытуемым).
Слайд 25Правила составления таблиц
Таблицы (её строки и столбцы) должны обязательно иметь
название (заголовок), если необходимо, то с указанием единиц измерения.
Таблицы
нумеруют. Точка как знак препинания при оформлении таблиц не ставится.
На все таблицы должны быть ссылки в тексте работы. При ссылке на таблицу следует писать слово «таблица» с указанием ее номера. Например, см. табл. 1. Нумеровать таблицы можно в пределах конкретного раздела, например, см. таблицу 1.2. , или иметь сквозную нумерацию.
Слайд 264. Таблица должна быть краткой, обозримой, включать только те показатели,
которые далее будут анализироваться исследователем. Если показателей много, то лучше
составить несколько таблиц.
5. Если таблица занимает более чем одну страницу (имеет большое количество строк), графы таблицы должны быть обязательно пронумерованы, а на следующих страницах печатаются только номера этих граф без заголовков. В этом случае, в правом верхнем углу указывают, продолжением какой таблицы является перенесенная часть строк. Например: «продолжение таблицы 1» или «окончание таблицы 1».
Слайд 276. Строки и столбцы располагаются в логичном порядке и по
необходимости нумеруются. Например, от общих показателей к частным или наоборот;
от числовых данных к качественным; от демографических данных к другим показателям и т.п.
7. Таблица не должна содержать пустых клеток. В случаях если данных нет, ставят «…», если изучаемое явление отсутствует – «-», если расчёт параметра не имеет смысла ставят «х», нулевое значение показателя «0».
Слайд 28Таблица 1.2 - Мотивы учебной деятельности студентов заочного отделения на
констатирующем этапе эксперимента
Слайд 29Виды таблиц. Сводные таблицы (таблицы исходных данных)
С них начинается
процесс представления данных. В них можно вносить не только числовые,
но и качественные данные, а также простые способы обработки информации (средние значения по выборке, суммы, частоты и т.п.).
Таблица 1.3 - Сводная таблица данных по экспериментальной выборке
Примечание:
1. Методика 1 - «Какой я есть и буду?» (модифицированный вариант) Р.С. Немов.
2. Методика 2 - «Фотозагадки». Н.Л. Белопольская.
3. Методика 3 - «Автопортрет». Р. Бернс (адаптирован Е.С. Романовой и С.Ф. Потемкиной).
4. Методика 4 - «Методика половозрастной идентификации». Н.Л. Белопольская.
Слайд 30Таблицы сопряжённости данных. Таблица, которая содержит сводную числовую характеристику по
двум и более качественным признакам или сочетанию количественного и качественного
признаков по выборке.
Таблица 4 - Таблица (2х2) сопряжённости данных по показателям роста сыновей и отцов
Слайд 31Составляются исследователем для того, чтобы изучить и наглядно представить, как
часто встречается то или иное значение признака, которое интересует исследователя.
Выделяют таблицы абсолютных частот (указывается, сколько раз встречается каждое значение признака), относительных частот (в них фиксируется доля наблюдений, которая приходится на то или иное значение признака), накопительных частот. Показывают, как накапливается частота по мере возрастания значения признака.
Таблицы распределения частот.
Таблица 1.6 - Распределение обращений на телефон доверия в течение недели
Слайд 32Графические формы представления данных исследования
График всегда строится на основе числовых
данных, которые содержатся в таблицах, он наглядно отображает показатели и
зависимости, представленные в ней.
Основными формами графического представления данных выступают гистограмма, полигон, кумулята, диаграмма.
Слайд 33Понятие о выборочных совокупностей
Выборка (выборочная совокупность) – совокупность отобранных единиц,
объединённых каким–либо общим признаком, который интересует исследователя.
Это часть генеральной
совокупности. Множество значений (n), извлечённых случайным способом из генеральной совокупности.
Слайд 34 Характеристика выборочных совокупностей
Выборки бывают:
малые (до 30 единиц);
средние (от 31 до 200 ед.);
большие (201 до ∞).
простые (однородные),
сложные (неоднородные).
Основной характеристикой выборки является её репрезентативность.
Слайд 35Характеристика выборочных совокупностей
Репрезентативность выборки
(от фр. representatif - представительный) –
представительность выборки.
Репрезентативность определяется:
А) количеством единиц (Репрезентативна та выборка, объём которой
составляет 10% и более от объёма генеральной совокупности)
Б) равной вероятностью отбора каждой единицы совокупности в выборку (применение процедуры рандомизации, связанной с использованием методов лотереи, случайных чисел и т.п, что обеспечивает случайность попадания в выборку каждой её единицы ).
Чем ближе объём выборки к генеральной совокупности, тем точнее результат, но тем больше вероятность ошибок.
Слайд 36Понятие об измерении
Измерение – это приписывание числовых форм (чисел) объектам
или событиям в соответствии с определёнными правилами.
Основой теории измерения выступает
психометрия.
Основными понятиями теории измерения являются: измерительная шкала, ряд распределения, показатель.
Слайд 37Понятие об измерении
Измерительная шкала (от лат. scala – лестница) –
основной инструмент психологического измерения, который в качестве эталона служит средством
фиксации определённой совокупности значений, которая интересует исследователя.
Стивенс С. выделил четыре способа измерения (4 вида измерительных шкал): номинальную (наименований); порядковую; интервальную; шкалу отношений.
Слайд 38Номинальная шкала (от лат. nomen – имя) – классифицирует объекты
по названию.
Название не измеряет количественно, но позволяет отличать один
объект от другого или одного субъекта от других. К видам номинальных шкал относятся дихотомические (альтернативных признаков) шкалы, шкалы трёх и более ячеек.
Измерение по своей сути сводится к группировке объектов по ячейкам, классам, группам при условии, что объекты, отнесённые к одной группе, идентичны, а отнесённые к разным группам различны.
Слайд 39Наиболее типичным применением номинальной шкалы является обработка социальных анкет, которые
содержат множество признаков, таких как пол, профессия, состав семьи, хобби,
удовлетворённость услугами, предоставляемыми супермаркетом или дошкольной образовательной организацией, которое посещает ребёнок респондента.
К результатам измерения в номинальной шкале можно применить лишь небольшое число методов математической обработки.
Слайд 40Порядковая (ранговая, ординальная) шкала – измерительная шкала, предназначенная для сравнения
интенсивности проявления признака по возрастанию или убыванию.
Измерение в этой
шкале предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства.
Классификация осуществляется по принципу «больше – меньше», «сильнее – слабее», тем самым образуется последовательность ячеек (классов) от самого малого значения признака к классу с самым большим значением (или наоборот).
Слайд 41Порядковая шкала
Расстояние между классами значения не имеет, важна лишь последовательность
значений, которую они образуют.
Чем больше мы имеем классов, тем
легче в последующем перейти к математической обработке и проверке статистических гипотез.
К данным может применяется процедура ранжирования.
Слайд 42Правила ранжирования переменных
Меньшему значению начисляется меньший ранг – ранг 1,
наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений.
В случае если
несколько значений равны, им начисляется ранг средний из тех, который они получили, если бы не были равны.
Общая сумма рангов должна совпасть с расчётной суммой, которая определяется по формуле:
Несовпадение реальной и расчётной суммой (полученной по формуле) будет свидетельствовать об ошибке при ранжировании переменных!
Слайд 44Интервальная шкала – метрическая шкала, позволяет сказать, насколько больше или
меньше выражен признак.
Измерение в данной шкале предполагает наличие единицы
измерения (метрики), а основным понятием является интервал (доля или часть измеряемого признака).
Размер интервала - величина фиксированная, а при равноинтервальном измерении постоянная на всех участках шкалы.
Особенностью шкалы является отсутствие естественной точки отсчёта.
Слайд 45Шкала интервалов
Принцип построения большинства интервальных шкал связан с правилом «трёх
сигм», согласно которому при нормальном распределении признака все значения укладываются
в диапазон М ± 3σ.
Примерами интервальных шкалах являются шкала Цельсия, стеновая шкала, IQ шкала Векслера и др.
Слайд 46Шкала отношений
Шкала отношений (абсолютная, равных отношений) – классифицирует объекты пропорционально
степени выраженности измеряемого свойства.
Данная шкала очень близка к интервальной
шкале, но позволяет сказать, во сколько раз признак более выражен.
Шкала является наиболее информативной и позволяет применять любые математические операции, однако в психологических исследованиях применяется редко.
Слайд 47Измерительные шкалы
Неметрические
(«слабые», нестрогие)
Метрические
(«сильные», строгие, количественные)
шкалы
наименований и порядка
шкалы
интервалов и отношений
Повышение мощности шкалы
Понижение мощности шкалы
Слайд 50Стандартизация и нормирование тестовых показателей
Стандартизация – это перевод первичных тестовых
показателей («сырых» баллов) в стандартные показатели.
Главная проблема стандартизации теста
заключается в разработке такой шкалы, в которой распределение тестовых показателей соответствовало бы закону нормального распределения.
Слайд 51Стандартизация и нормирование тестовых показателей
Стандарт – это единичное нормальное распределение
значений признака (Хi), данное в терминах отклонений от среднего (М)
в единицах стандартного отклонения (σ).
Норма - это таблица данных в вид процентилей, стенов или других стандартных оценок, полученных на определённой выборке.
!Нормирование тестовых показателей проводится только на больших (более 200 наблюдений) репрезентативных выборках. Выборка обязательно проверяется на её соответствие закону нормального распределения с помощью специальных статистических критериев
Слайд 52Стандартизация и нормирование тестовых показателей
Стеновая шкала (от англ. st… сокращение
от standart + ten – десять = стандартная десятка) принимает
значения от 1 до 10.
Шкала предложена Р. Кеттеллом со средним М = 5,5 и стандартным отклонением (σ) = 2. Среднее арифметическое значение в «сырых» баллах принимается за точку отсчёта. В правую и в левую стороны от среднего значения откладываются по 5 интервалов с шагом h = σ.
Слайд 53Таблица - Таблица нормирования первичных («сырых») баллов по факторам А,
В, N методики Р. Кеттела. Женщины 19 – 28 лет
!
Слайд 54Стенайновая шкала разработана во время Второй мировой войны в ВВС
США. Стенайн (от англ. st… сокращение от standart + nine
– девять = стандартная девятка) принимает значение от 1 до 9 .
Это шкала одноразрядных оценок со средним М = 5 и стандартным отклонением σ = 2.
Слайд 55Таблица перевода первичных баллов в стенайны
Слайд 56IQ шкала Векслера. Первые тесты, показатели которых выражались в единицах
стандартного IQ, были шкалы интеллекта Векслера со средним М =
100 и стандартным отклонением σ = 15.
Следовательно, значение IQ выше 100, полученное по тесту Векслера, рассматривается как показатель выше среднего.
Слайд 57Шкала процентилей.
Процентильные показатели в равной мере подходят к любому
типу теста.
Процентили выражаются в единицах процента лиц, составляющих выборку
стандартизации, результат которых ниже установленной первичной оценки.
Например, если 28% людей решают правильно меньше 15 задач теста, то первичная «сырая» оценка 15 соответствует 28–му процентилю (Р28). Таким образом, процентили показывают относительное положение индивида в выборке стандартизации. 50–й процентиль (Р50) соответствует медиане, а процентили выше 50–го представляют результаты выше среднего.
Слайд 58Пример процедуры стандартизации
Принцип построения большинства интервальных шкал построен на основе
правила «трёх сигм», согласно которому 97,8% всех значений признака при
нормальном распределении укладываются в диапазон М ± 3σ.
В шкале стенов справа от среднего значения располагаются интервалы, равные 6, 7, 8, 9, 10 стенам, при этом последний интервал остаётся открытым. Слева от среднего значения располагаются интервалы, равные 5, 4, 3, 2 и 1 стенам, при этом крайний интервал также остается открытым
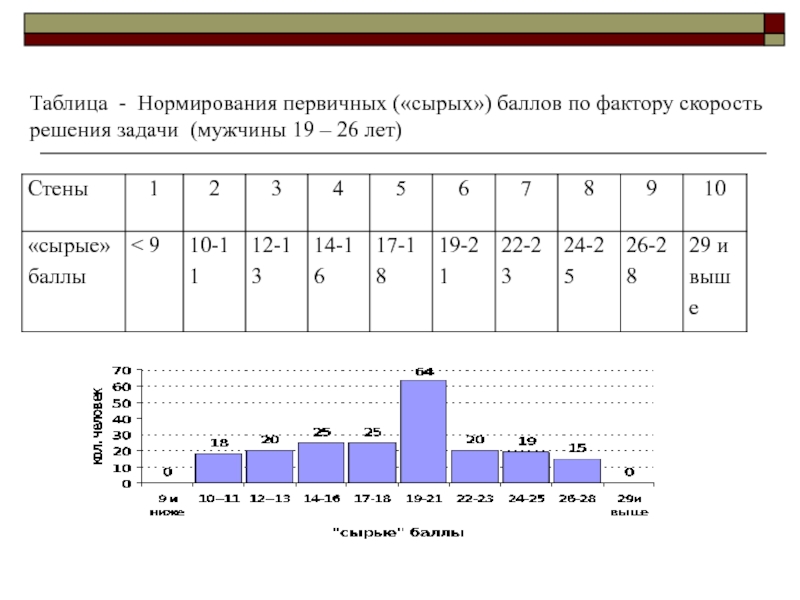
Слайд 59Пример: Проведено измерение скорости решения тестового задания на репрезентативной выборке
мужчин (n=206) возраста 19 – 26 лет. Результаты измерения представлены
в таблице
N = 206; σ = 4,8; М = 18,6; h = ½σ = ??.
Слайд 60Таблица - Нормирования первичных («сырых») баллов по фактору скорость решения
задачи (мужчины 19 – 26 лет)
Слайд 61Простой способ стандартизации
На основании начисленных баллов определяем границы низких и
высоких баллов.
Граница низких баллов = m - ⅔σ,
граница
высоких баллов = m + ⅔σ.
Слайд 62Задача.
Результаты измерения уровня социальных эмоций детей среднего дошкольного возраста
N
= ?; σ = 2,9; М = ?;
h =??.
Слайд 63Вычисление среднего арифметического, среднего квадратичного отклонения
http://studlab.com/news/vychislenie_srednego_znacheni..
Показатели вариации (средняя, мода
(в т.ч. и графическим способом), медиана, размах вариации, квартили, децили,
квартильный коэффициент дифференциации, коэффициент вариации)
http://math.semestr.ru/group/group.php
χ2 - критерий Пирсона (реализация, как в программе SPSS - необходимо вставлять имеющиеся ряды чисел) http://www.psychol-ok.ru/statistics/pearson/
Коэффициент вариации http://planetcalc.ru/688/
Коэффициент корреляции Спирмена http://www.spearman.ru/ru/correlation_analysis/spearm..
Коэффициент корреляции Пирсона http://planetcalc.ru/527/
Т-критерий Стьюдента для независимых и зависимых выборок
http://www.psychol-ok.ru/statistics/student/
Т -критерий Вилкоксона http://www.psychol-ok.ru/statistics/wilcoxon/
G критерий знаков
http://www.infamed.com/stat/s03.html
U-критерий Манна-Уитни
http://www.psychol-ok.ru/statistics/mann-whitney/