Слайд 1Тема.
Арифметико-логические устройства, микропроцессоры
Слайд 2Сумматоры
По числу выводов различают: полусумматоры, одноразрядные сумматоры, многоразрядные сумматоры.
Полусумматор -
устройство для сложения двух одноразрядных кодов, имеет два входа и
два выхода и формирующее из сигналов входных слагаемых сигналы суммы и переноса в старший разряд.
Однозарядный сумматор – устройство для сложения двух одноразрядных кодов, имеющее три входа и два выхода, и формирующее из сигналов входных слагаемых и сигнала переноса из младших разрядов сигналы суммы и переноса в старший разряд.
Многоразрядный сумматор – устройство для сложения двух многоразрядных кодов, формирующее на выходе код суммы и сигнал переноса в случае, если результат сложения не может быть представлен кодом, разрядность которого совпадает с разрядностью кодов слагаемых.
Многоразрядные сумматоры подразделяются на последовательные и параллельные. В последовательных сумматорах операция сложения выполняется последовательно разряд за разрядом, начиная с младшего. В параллельных все разряды входных кодов суммируются одновременно.
Слайд 3Различают комбинационные сумматоры — устройства, не имеющие собственной памяти, и
накапливающие сумматоры, снабжённые собственной внутренней памятью, в которой аккумулируются результаты
выполненной операции. При этом каждое очередное слагаемое прибавляется к уже имевшемуся в устройстве значению.
По способу тактирования различают синхронные и асинхронные сумматоры. В синхронных сумматорах время выполнения операции арифметического суммирования двух кодов не зависит от вида самих кодов и всегда остается постоянным. В асинхронных сумматорах время выполнения операции зависит от вида слагаемых. Поэтому по завершении выполнения суммирования необходимо вырабатывать специальный сигнал завершения операции.
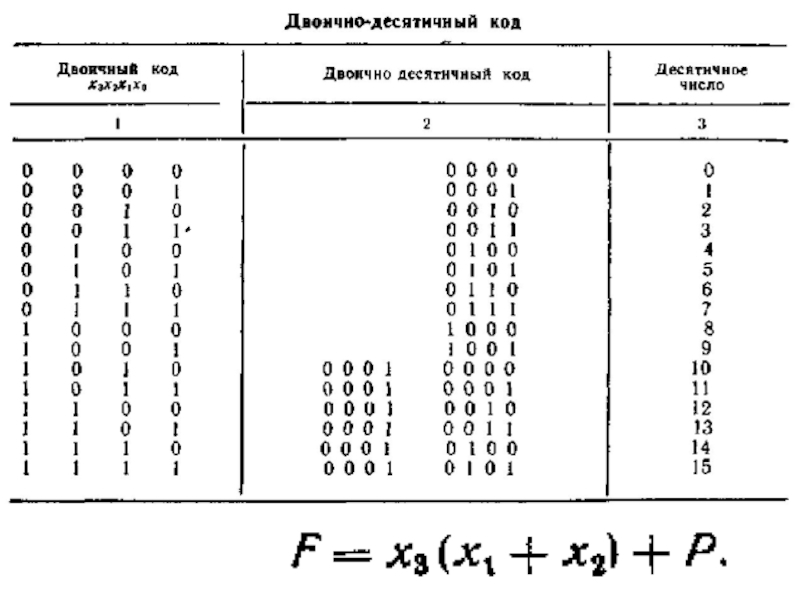
В зависимости от используемой системы счисления различают двоичные, двоично-десятичные и другие типы сумматоров.
Слайд 4Сложение одноразрядных двоичных кодов - операция "Исключающее ИЛИ" над исходным
слагаемыми х1 и x0.
Сумматор - один из основных узлов арифметико-логического
устройства. Термин сумматор охватывает широкий спектр устройств от простейших логических схем, до сложнейших цифровых узлов. Общим для этих устройств является арифметическое сложение двоичных чисел
Слайд 5Сложение многоразрядных двоичных кодов.
Для получения суммы двух старших разрядов необходимо
сначала выполнить операцию Исключающее ИЛИ над исходным слагаемыми х1 и
x0 и затем еще одну операцию Исключающее ИЛИ над результатом первой операции Исключающее ИЛИ и сигналом переноса из предыдущего разряда. Для получения сигнала переноса также необходимо воспользоваться результатом операции Исключающее ИЛИ над слагаемыми х1 и x0.
Слайд 6Структурная схема реализации двоичного полусумматора
х0
ДВОИЧНЫИ ПОЛУСУММАТОР - устройство сложения двух
одноразрядных кодов, имеет два входа и два выхода, формирует из
сигналов входных слагаемых сигналы суммы и переноса в старший разряд.
Структурная схема реализации операции «Исключающее ИЛИ»
Время операции
Слайд 7ОДНОРАЗРЯДНЫЙ СУММАТОР - устройство, предназначенное для сложения двух одноразрядных кодов,
имеющее три входа и два выхода, и формирующее из сигналов
входных слагаемых и сигнала переноса из младших разрядов сигналы суммы и переноса в старший разряд.
Время суммирования и приведённой схеме также определяется временем выполнения операции Исключающее ИЛИ
Формирование сигнала переноса в старший разряд выполняется быстрее
Время операции
Слайд 8МНОГОРАЗРЯДНЫЙ СУММАТОР - устройство сложения двух многоразрядных кодов, формирующее на
выходе код суммы и сигнал переноса в случае, если результат
сложения не может быть представлен кодом, разрядность которого совпадает с разрядностью кодов слагаемых.
Многоразрядные сумматоры подразделяются на последовательные и параллельные.
Слайд 12АЛГОРИТМ ВЫЧИТАНИЯ ДВОИЧНЫХ ЧИСЕЛ
Известно, что операцию вычитания двух чисел можно
заменить операцией сложения, если в качестве вычитаемого взять число, противоположное
по знаку исходному. Поэтому для выполнения операции вычитания можно использовать схемы сумматоров.
Для представления отрицательных чисел наибольшее распространение получил метод, в котором для обозначения знака используется старший разряд его двоичного кода. Так, если используется 8-разрядный двоичный код, то семь его разрядов содержат информацию о величине (модуле) числа, а восьмой (старший)— о его знаке: присутствие в этом разряде нуля означает положительное число , присутствие единицы —отрицательное. Используя 8-разрядный код, можно записать числа с десятичными эквивалентами от —127 до +127.
Присутствие знакового разряда непосредственно не позволяет использовать рассмотренные схемы сумматоров для выполнения операции вычитания чисел, представленных в прямом двоичном коде. Наиболее часто для записи отрицательного числа используется дополнительный код.
Алгоритм получения дополнительного кода двоичного числа :
- записывают обратный код исходного числа (все его разряды инвертируют -заменяют дополнениями);
- к полученному после инвертирования коду добавляют единицу.
Далее, при сложении полученного таким образом кода вычитаемого с кодом уменьшаемого будет реализована операция вычитания. Знак результата определяет старший разряд полученного кода. Если старший разряд равен нулю, получено положительное число, представленное в прямом коде. Если старший разряд равен единице, получено отрицательное число, представленное в дополнительном коде.

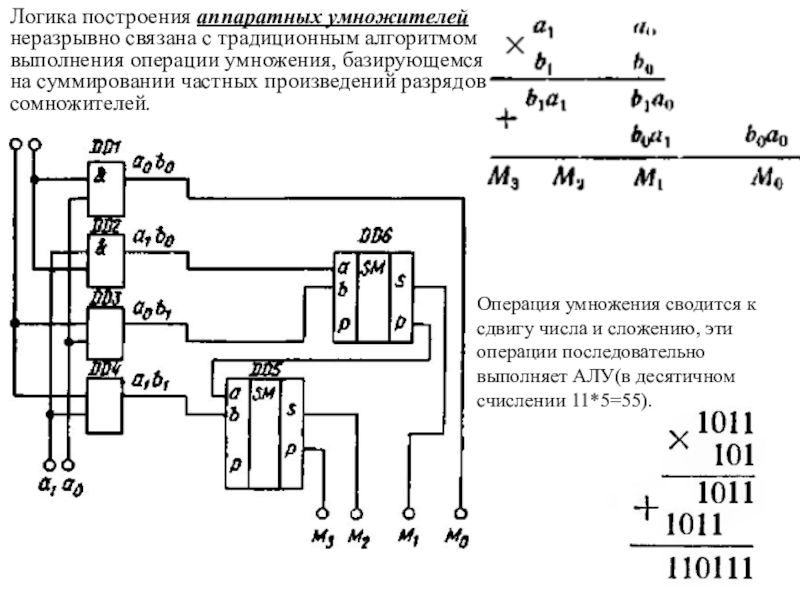
Слайд 17Логика построения аппаратных умножителей неразрывно связана с традиционным алгоритмом выполнения
операции умножения, базирующемся на суммировании частных произведений разрядов сомножителей.
Операция
умножения сводится к сдвигу числа и сложению, эти операции последовательно выполняет АЛУ(в десятичном счислении 11*5=55).
Слайд 21Арифметико-логическое устройство (АЛУ) — часть центрального процессора, формирующая функции двух
входных переменных и порождающая одну выходную переменную. Эти функции состоят
из простых арифметических и (или) логических операций, операций сдвига.
Вне зависимости от того, насколько широк круг операций, реализуемых современными АЛУ, главными среди них остаются операции арифметического сложения и умножения, продолжительность выполнения которых указывается в качестве основных характеристик вычислительного устройства.
Простейшие операции: арифметичес-кое сложение (вычитание), логическое умножение, логическое сложение, сумма по модулю два, инверсия, сдвиг влево, сдвиг вправо, инкремент (положитель-ное приращение), декремент (отрица-тельное приращение) выполняются в АЛУ с помощью аппаратных средств (схем на логических элементах).
Операция умножения (деления), как правило, выполняется программным способом (с применением последовательного исполнения нескольких операций сложения и сдвига), выполненных аппаратным способом.
Слайд 22По способу действия над операндами АЛУ подразделяют на параллельного и
последовательного действия.
По способу представления чисел различают АЛУ для чисел с
фиксированной и плавающей запятой (точкой), для десятичных чисел.
По способу организации работы АЛУ делят на синхронные и асинхронные
По характеру используемых элементов и узлов: универсальные, в которых операции для всех форм представления чисел выполняются одними и теми же схемами, и функциональные, в которых операции над операндами с фиксированной и плавающей запятой, с десятичными переменными и логическими переменными осуществляются в отдельных операционных блоках.
По связи с оперативной памятью (ОЗУ) вычислительного устройства различают АЛУ с непосредственной и магистральной связями.
В АЛУ с непосредственной связью схемы управления передачей информации соединены непосредственно с выходами регистров, а в АЛУ с магистральной связью схемы для преобразования информации выделены в отдельные блоки с двумя шинами (входной и выходной), а регистры служат лишь для хранения операндов во время их обработки. АЛУ с магистральной связью используется в процессорах с микропрограммным управлением.

Слайд 23Современная технология изготовления ИМС позволяет выполнить весьма сложные электронные устройства
в виде одной или нескольких ИМС. Такое техническое решение будет
экономически выгодным, если данное устройство будет производиться массовыми сериями, но, как правило, сложные специализированные устройства не требуется производить в большом числе экземпляров. Это противоречие между возможностями технологии и узкой специализированностью сложных электронных устройств снимается при создании программируемых цифровых и логических устройств.
Подобные устройства основаны на работе арифметико-логического устройства (АЛУ), которое выполняется как самостоятельная БИС либо входит в состав других более сложных ИМС. АЛУ позволяет производить арифметические и логические операции над «n-разрядными входными кодами (4, 8 или 16); входные коды обозначены А (А1А2А3А4) и В (B1B2B3B4). Сигналы, подаваемые на управляющие входы М, S0, Si, S2, S3, определяют, какая именно операция может быть выполнена над входными величинами. Как и в многоразрядном сумматоре, при выполнении арифметических операций на АЛУ может быть подан сигнал переноса из внешней цепи (Р0=1), который добавляется в младший разряд АЛУ, на выходе АЛУ формируется сигнал И4, переноса из старшего разряда (сигнал переполнения). Сигнал переноса Ро—l увеличивает результат (число F) на единицу. АЛУ представляет собой логическую схему, имеющую определённое количество входов (Лг, Bi, М, S,- и Ро) и выходов (Fi, Рп), где Fi — результаты операций в каждом разряде, Рп — сигнал переноса из старшего разряда. Сово-купность сигналов на всех входах однозначно определяет совокупность выходных сигналов, поэтому АЛУ является комбинационным устройством.

Слайд 24При управляющем сигнале М=0 АЛУ выполняет арифметические операции над входными
n-разрядными двоичными числами А к В: сложение А и В,
сложение А и В с добавлением единицы в младший разряд из внешней цепи (сигнал Р0= 1), вычитание В из А, вычитание В из А с учётом знаема единицы из младшего разряда, увеличение или уменьшение числа А на единицу, пересылка чисел А и В с входа АЛУ на выход, сдвиг чисел на один разряд влево (эквивалентно умножению на два) или вправо (эквивалентно делению на два) и др. Комбинация сигналов SC...S3 определяет, какая именно математическая операция производится АЛУ.
При М=1 АЛУ выполняет логические операции над функциями А и В (во всех разрядах выполняется одна и та же логическая операция).
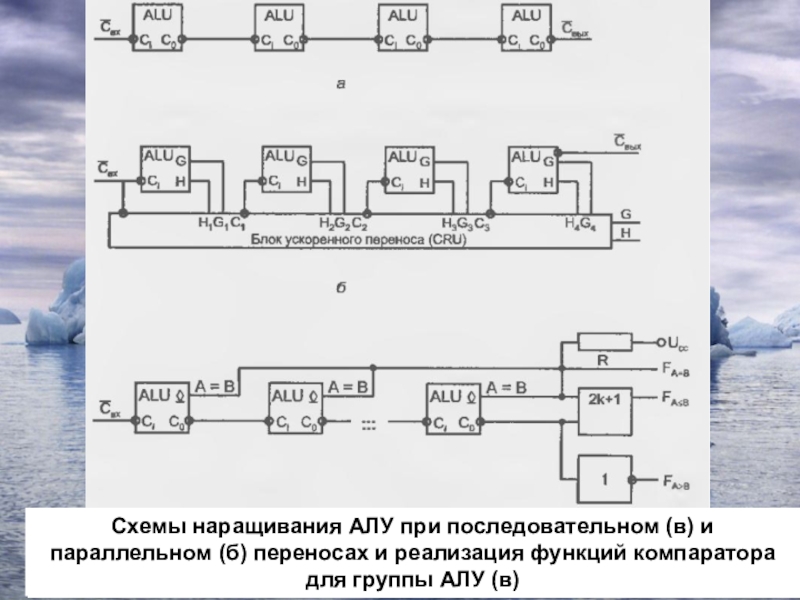
Слайд 26Схемы наращивания АЛУ при последовательном (в) и параллельном (б) переносах
и реализация функций компаратора для группы АЛУ (в)
Слайд 27Несмотря на разнообразие операций, выполняемых АЛУ, его функциональность ограниченна: устройство
выполняет только операции над двумя переменными, отсутствуют арифметические операции умножения
и деления и т. п. Преодоление этой ограниченности достигнуто в микропроцессорах,
Микропроцессор - программно-управляемое устройство для обработки цифровой информации и управления этим процессом.
Характеристики:
Разрядность.
Производительность.
Система команд.
Объем адресуемой памяти.
Группы микропроцессоров:
CISC - полный набор команд.
RISC - сокращённый набор команд.
MISC - минимальный набор команд, очень высокое быстродействие
МП состоит из двух частей:
Операционная: устройства управления, арифметико-логическую и микропроцессорную память.
Интерфейсная: адресные регистры, схемы управления портами и шиной, а также блок команд.
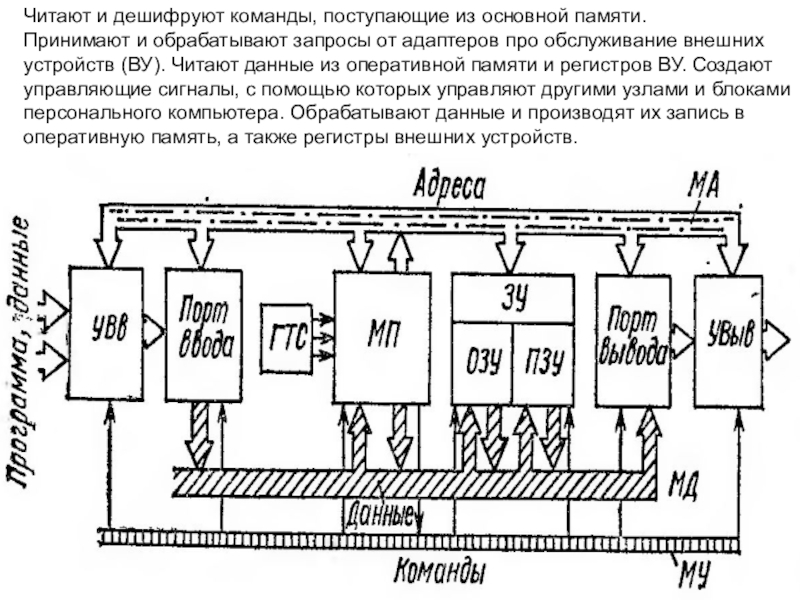
Слайд 28Читают и дешифруют команды, поступающие из основной памяти.
Принимают и обрабатывают
запросы от адаптеров про обслуживание внешних устройств (ВУ). Читают данные
из оперативной памяти и регистров ВУ. Создают управляющие сигналы, с помощью которых управляют другими узлами и блоками персонального компьютера. Обрабатывают данные и производят их запись в оперативную память, а также регистры внешних устройств.
Слайд 31Микросхемы множительных устройств появились в 1980-х годах, когда достигнутый уровень
интеграции позволил разместить на одном кристалле достаточно большое количество логических
элементов.
Структура матричных умножителей тесно связана со структурой математических выражений, описывающих операцию умножения.
Пусть имеются два целых двоичных числа без знаков Аm = аm-1...ао и Вn = bn-1...bо, Их перемножение выполняется по известной схеме "умножения столбиком". Если числа четырехразрядные, т. е. m = n = 4, то
Слайд 32Произведение выражается числом Рm+n = Рm+n-1 Pm+n-2 … Ро.
Члены вида
аibj, где i = 0... (m-1) и j = 0...
(n-1) вырабатываются параллельно во времени конъюнкторами. Их сложение в столбцах, которое можно выполнять разными способами, составляет основную операцию для умножителя и определяет почти целиком время перемножения.
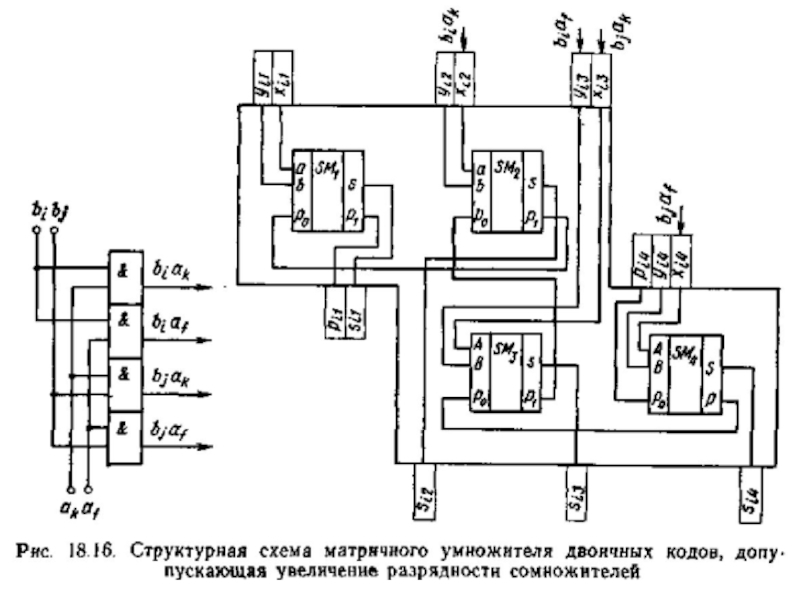
Матричные перемножители могут быть просто множительными блоками (МБ) или множительно-суммирующими (МСБ), последние обеспечивают удобство наращивания размерности умножителя.
МСБ реализует операцию Р = Аm х Вn + Сm + Dn, т. е. добавляет к произведению два слагаемых: одно разрядности m, совпадающей с разрядностью множимого, другое разрядности n, совпадающей с разрядностью множителя.
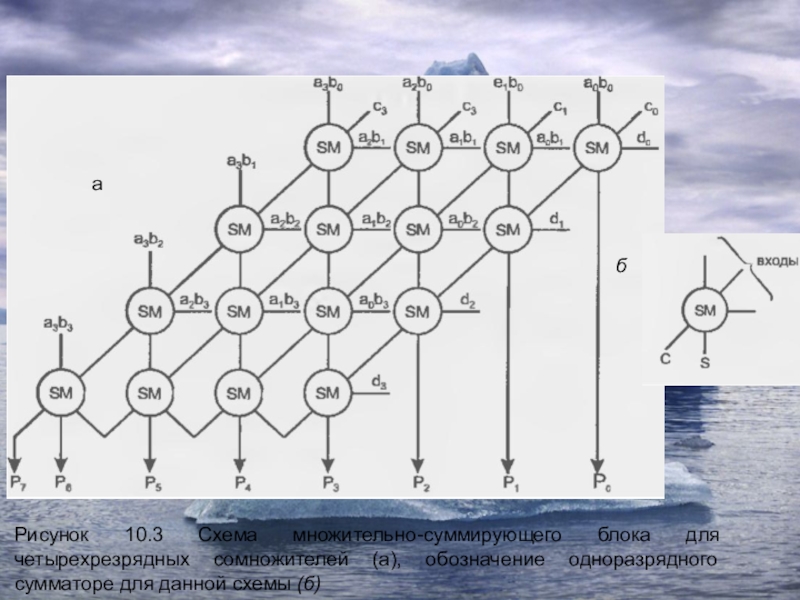
Слайд 33Множительно-суммирующие блоки
Множительно-суммирующий блок для четырехразрядных операндов без набора конъюнкторов, вырабатывающих
члены вида аibj, показан на рис. 2.37, а, где для
одноразрядного сумматора принято обозначение (рис. 2.37, б).
Для построения МСБ чисел равной разрядности потребовалось n2 конъюнкторов и n2 одноразрядных сумматоров.
Слайд 34Рисунок 10.3 Схема множительно-суммирующего блока для четырехрезрядных сомножителей (а), обозначение
одноразрядного сумматоре для данной схемы (б)
а
б
Слайд 35Рисунок 10.4 К пояснению принципа наращивания размерности множительных устройств (в),
условное обозначение множительно-суммирующего блока
Слайд 36Рисунок 10.5 схема умножителя 4x4", построенная на множительно-суммирующих блоках "4
х 2" (в)
Слайд 37Максимальная длительность умножения — сумма задержек сигналов в конъюнкторах для
выработки членов аibj и задержки в наиболее длинной цепочке передачи
сигнала в матрице одноразрядных сумматоров, равной 2n - 1 (m + n - 1 в общем случае). Таким образом, tМРL = tк + (2n - 1)tsм,
Схема множительного блока отличается от схемы МСБ тем, что в ней отсутствуют сумматоры правой диагонали, т. к. при Сm = 0 и Dn = 0 они не требуются.
Построение умножителей большей размерности из умножителей меньшей размерности на основе МБ требует введения дополнительных схем, называемых "деревьями Уоллеса", которые имеются в некоторых зарубежных сериях. При использовании МСБ дополнительные схемы не требуются. Принцип наращивания размерности умножителя иллюстрируется на рис. 2.38, а на примере построения МРЬ "4 х 4" из МСБ "4 х 2". На поле частичных произведений выделены зоны, воспроизведение которых возможно на блоках размерности 4x2 (это две первые строки и две последние).
Перемножение в пределах зон дает частичные произведения р1 = Р51Р41РЗ1Р21Р11Р01 и Р2 = Р52Р42Р32Р22Р12Р02. Для получения конечного значения произведения эти частичные произведения нужно сложить с учетом их взаимного положения (сдвига одного относительно другого).
Схема, реализующая указанный принцип, изображена на рис. 2.38, в. В ней использовано условное обозначение МСБ (рис. 2.38, б). Для общности оба блока размерности 4x2 показаны как МСБ, хотя первый может быть просто множительным блоком, т. к. для него слагаемые С и D имеют нулевое значение.

Слайд 38Схемы ускоренного умножения
Для ускорения умножения разработан ряд алгоритмов, большой вклад
в эти разработки внес Э. Бут (Е. Вооt). Рассмотрим процесс
умножения по гак называемому модифицированному алгоритму Бута (умножение сразу на два разряда).
Из изложенного выше видно, что основную задержку в процесс выработки произведения вносит суммирование частичных произведений. Уменьшение их числа сократило бы время суммирования. К этому приводит алгоритм, основанный на следующих рассуждениях.
Пусть требуется вычислить произведение
(a)
Слайд 39Непосредственное воспроизведение соотношения (а) связано с выработкой частичных произведений вида
Abj2i (i = 0...n - 1). Число таких произведений равно
разрядности множителя n.
Выражение (а) можно видоизменить с помощью соотношения
(б)
справедливость которого очевидна.
Это соотношение позволяет разреживать последовательность (спектр) степеней в сумме частичных произведений. Можно, например, исключить четные степени, как показано на рис. 2.39, а. Исключение четных (или нечетных) степеней не только изменяет значения оставшихся частичных произведений, но и сокращает их число примерно вдвое, что, в конечном счете, ускоряет выработку произведения. Для того чтобы "разнести по соседям" член со степенью 2°, расширим разрядную сетку, введя слагаемое
b-12-1 (нулевой разряд с номером -1).
Оставшиеся частичные произведения имеют вид
Так как число частичных произведений уменьшилось примерно вдвое, при применении этого алгоритма говорят об умножении сразу на два разряда.
Слайд 40Рисунок 10.6 К пояснению принципа быстрого умножения "срезу на два
разряда" (в) и схема быстрого умножения (б)
Слайд 41 Для всех возможных сочетаний bi+1, bi, bi-1 можно
составить таблицу (табл. 2.14) частичных произведений.
Слайд 42Пример
Пусть требуется умножить 10102 на 01112, т. е. 10 х
7. При разреживании частичных произведений оставим только нечетные, как показано
на рис. 2.39, а Расширив разрядную сетку множителя, имеем В = b4b3b2b1b0b-1b-2 = 0011100.
Первому частичному произведению соответствует тройка b0b-1b-2 = 100. Из табл. 2.14 получаем, что этой тройке соответствует частичное произведение — -2А 2-1 = - А. для получения которого требуется перевести А в дополнительный код. Сама величина А в пределах разрядной сетки произведения должна быть записана как 00001010, ее обратный код 11110101 и дополнительный код 11110110.
Второму частичному произведению соответствует тройка b2b1b0 =111. следовательно, второе частичное произведение равно нулю (табл. 2.14).
Третьему частичному произведению соответствует тройка b4b3b2 = 001, следовательно, оно имеет вид А 23 = 01010000
Для получения результата заданного умножения требуется сложить частичные произведения:
Слайд 43Схема, реализующая алгоритм быстрого умножения сразу на два разряда, показана
на рис. 2.39, б.
Множимое А поступает в этой схеме на
ряд преобразователей, заготавливающих все возможные варианты частичных произведений (-2А, -А, 2А), кроме самого А и нуля, которые не требуют схемной реализации. Множитель В поступает на логический преобразователь ЛП, который анализирует тройки разрядов, декодирует их и дает мультиплексорам сигналы выбора того или иного варианта частичных произведений. Окончательный результат получается суммированием частичных произведений с учетом их взаимного сдвига в разрядной сетке. Размерность умножителя "4 х 4".
Приведенные выше примеры множительных устройств касались операций с прямыми кодами. В этом случае умножение знакопеременных чисел сведется только к выработке знакового разряда как суммы по модулю 2 знаковых разрядов сомножителей. Если же числа представлены не прямыми колами с знаковыми разрядами, а, например, дополнительными кодами, то, имея рассмотренные выше умножители, можно дополнить их преобразователями дополнительного кода в прямые на входах и преобразователем прямого кода в дополнительный на выходе или использовать схемы, непосредственно реализующие алгоритмы умножения дополнительных кодов (см., например, [37]).
Разработке матричных умножителей уделяют внимание многие фирмы. В отечественных сериях МИС/СИС имеются умножители малой размерности (2 х 2, 4 х 4, 4 х 2 и др.). В сериях БИС размерности умножителей знвчительно больше. В серии 1802, например, имеются умножители 8x8, 12x12, 16x16 (ВРЗ, ВР4 и ВР5 соответственно). В схемотехнике ЭСЛ выполнен умножитель 1800ВР1 (8 х 8 за 17 нc). Зарубежные фирмы разработали умножители (фирмы BIT, Нitachi и др.) размерностями 16 х 16 и более с временами умножения 3...5 нc. Несколько лет назад предприятие "Интеграл" (г. Минск) выпустило умножитель КА1843ВР1 размерностью 32 х 32 со временем умножения 250 нс в корпусе с 172 выводами.

Слайд 44Блок СКГ вырабатывает также функции генерации и прозрачности для всей
группы обслуживаемых им АЛУ, что при необходимости позволяет организовать параллельный
перенос на следующем уровне (между несколькими группами из четырех АЛУ).
На рис. 2.36, в показаны способы выработки сигналов сравнения слов для группы АЛУ. Выход сравнения на равенство выполняется по схеме монтажной логики для выходов типа ОК. Комбинируя сигнал равенства слов с сигналом переноса на выходе группы при работе АЛУ в режиме вычитания, легко получить функции FA≥B и FA≤B. Если А < В, то при вычитании возникает заем из старшего разряда и FA≤B = 1. Если заем отсутствует (А>В), то подучим FA≥B = 1.
Слайд 45блок регистров БРег, предназначенный для приёма и размещения операндов и
результата операции;
блок арифметико-логических операций БАЛО, в котором осуществляется преобразование операндов
согласно коду операции (КОП) в реализуемой команде;
блок контроля БКонтр, обеспечивающий непрерывный оперативный контроль и диагностику ошибок;
блок управления БУ, в котором формируются импульсы синхронизации ИС, координирующие взаимодействие всех блоков АЛУ между собой и с другими блоками процессора.
Слайд 46Устройство работает в соответствии с сообщаемыми ему кодами операций, которые
нужно выполнить над переменными, помещаемыми в регистры. На разных этапах
выполнения команды операции производится анализ преобразований информации, и на основании сигналов признаков ПР блок БУ формирует и выдаёт осведомительный сигнал ОС, характеризующий некоторое состояние процессора. В асинхронных АЛУ выполнение операции производится по сигналу НО (начало операции), а переход к выполнению очередной команды — по сигналу КО (конец операции).
В основе построения схем АЛУ положены одноразрядные комбинационные сумматоры, образующие при определённой коммутации 4разрядный сумматор с параллельным переносом.
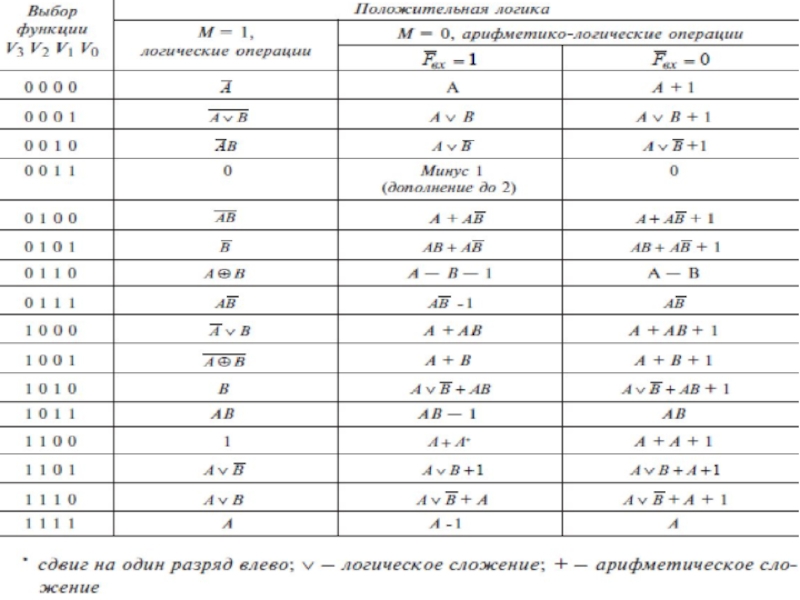
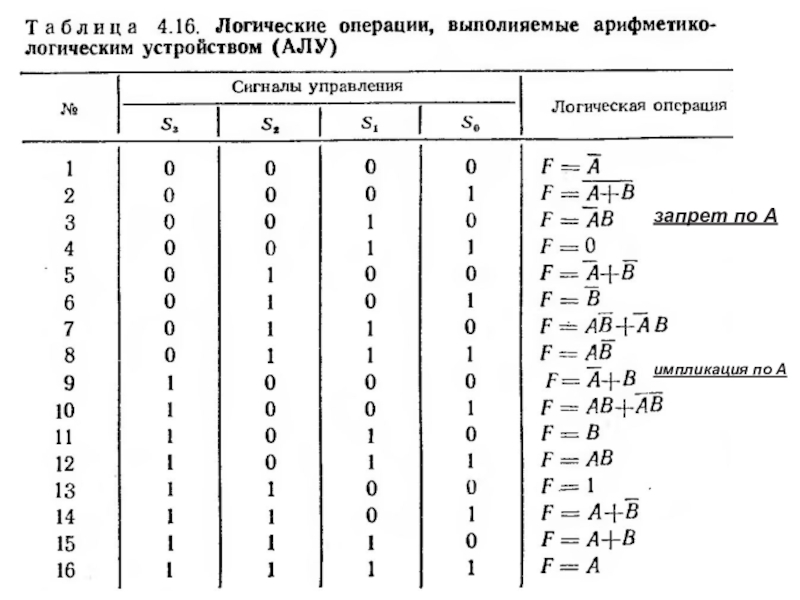
Каждая схема АЛУ обеспечивает выполнение над 4-разрядными
словами А и В шестнадцати поразрядных логических и
арифметико-логических операций (таблица 6.7).
Коммутация АЛУ на выполнение
той или иной из 16 операций в заданном режиме
производится управляющими сигналами V3V2V1V0
и сигналом М.
При М = 0 АЛУ выполняет арифметические операции, а
при М = 1 — логические. Комбинация входных
сигналов V3V2V1V0 определяет одну из
16 выполняемых функций.

Слайд 49Арифметико-логические устройства АЛУ (ALU, Arithmetic-Logic Unit) выполняют над словами ряд
действий. Основой АЛУ служит сумматор, схема которого дополнена логикой, расширяющей
функциональные возможности АЛУ и обеспечивающей его перестройку с одной операции на другую
Обычно АЛУ четырехразрядны и для наращивания разрядности объединяются с формированием последовательных или параллельных переносов. Логические возможности АЛУ разных технологий (ТТЛШ, КМОП, ЭСЛ) сходны. В силу самодвойственности выполняемых операций условное обозначение и таблица истинности АЛУ встречаются в двух вариантах, отличающихся взаимно инверсными значениями переменных
АЛУ (рис. 2.35) имеет входы операндов А и В, входы выбора операций S, вход переноса Ci и вход М (Моdе), сигнал которого задает тип выполняемых операций: логические (М = 1) или арифметико-логические (М = 0). Результат операции вырабатывается на выходах F, выходы G и Н дают функции генерации и прозрачности, используемые для организаций параллельных переносов при наращивании размерности АЛУ. Сигнал Со — выходной перенос, а выход А = В есть выход сравнения на равенство с открытым коллектором.
Рисунок 10.1 Условнее обозначение АЛУ

Слайд 50Шестнадцать логических операций позволяют воспроизводить все функции двух переменных. В
логико-арифметических операциях встречаются и логические и арифметические операции одновременно.
Запись типа
А\/В + АВ следует понимать так: вначале поразрядно выполняются операции инвертирования (В), логического сложения (А\/В) и умножения (АВ), а затем полученные указанным образом два четырехразрядных числа складываются арифметически.
При операциях над словами большой размерности АЛУ соединяются друг с другом с организацией последовательных (рис. 2.36, а) или параллельных (рис. 2.36, б) переносов. В последнем случае совместно с АЛУ применяют микросхемы — блоки ускоренного переноса (СRU, Саrrу Unit), получающие от отдельных АЛУ функции генерации и прозрачности, а также входной перенос и вырабатывающие сигналы переноса
Слайд 52Перечень выполняемых АЛУ операций дан в табл. 2.13. Для краткости
двоичные числа s3s2s1s0 представлены их десятичными эквивалентами. Под утолщенными обозначениями
1 и 0 следует понимать наборы 1111 и 0000, входной перенос поступает в младший разряд слова, т. е. равен 000Сi. Логические операции поразрядные, т. е. операция над словами А * В означает, что а; * Ь; при отсутствии взаимовлияния разрядов. При арифметических операциях учитываются межразрядные переносы.