Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кафедра Инженерной и машинной геометрии и графики (О3)
Содержание
- 1. Кафедра Инженерной и машинной геометрии и графики (О3)
- 2. Кафедра Инженерной и
- 3. Литература (основная):1. Фролов С.А. Начертательная геометрия. Учебник
- 4. Литература (дополнительная):Бубенников А.В. Начертательная геометрия. – М.:
- 5. Основатель «Начертательной геометрии» Г. Монж (1746-1818)
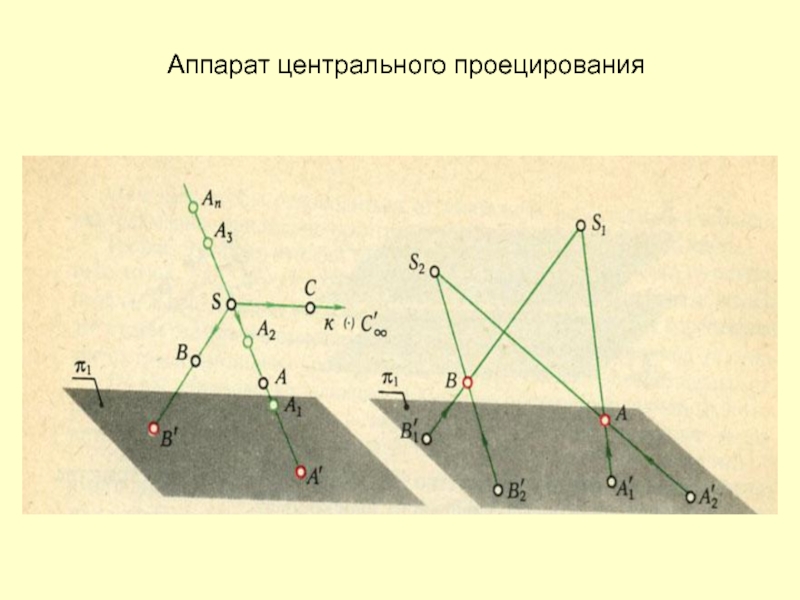
- 6. Аппарат центрального проецирования
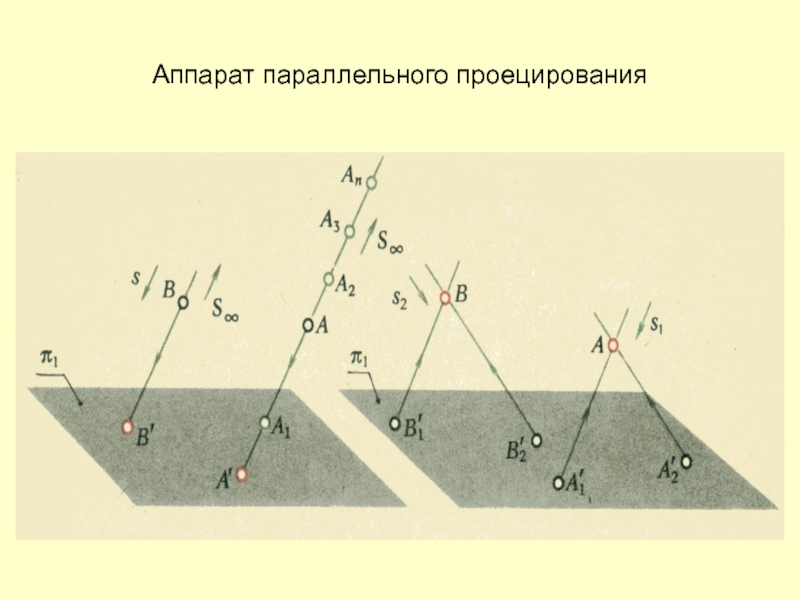
- 7. Аппарат параллельного проецирования
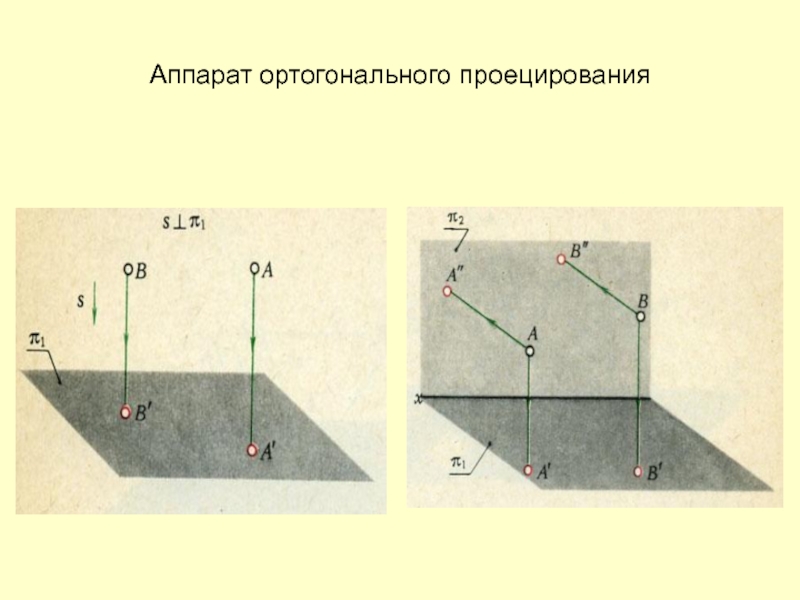
- 8. Аппарат ортогонального проецирования
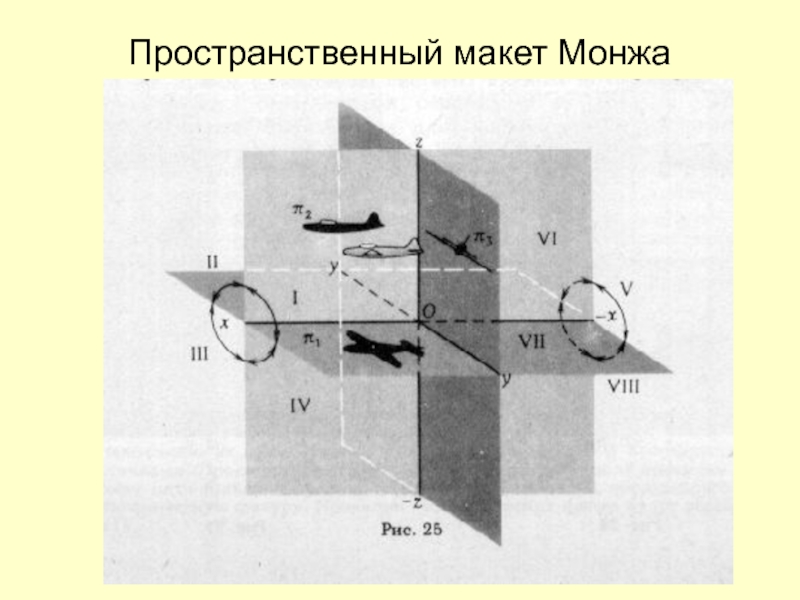
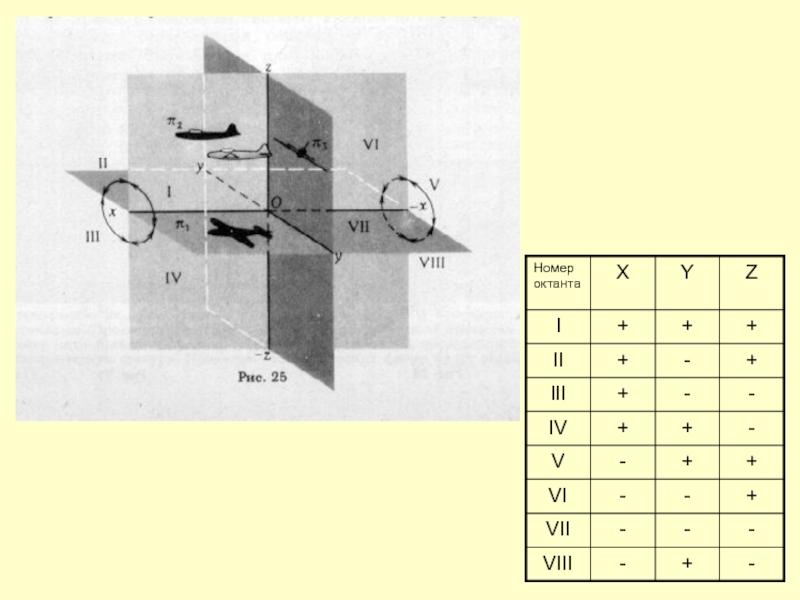
- 9. Пространственный макет Монжа
- 10. Слайд 10
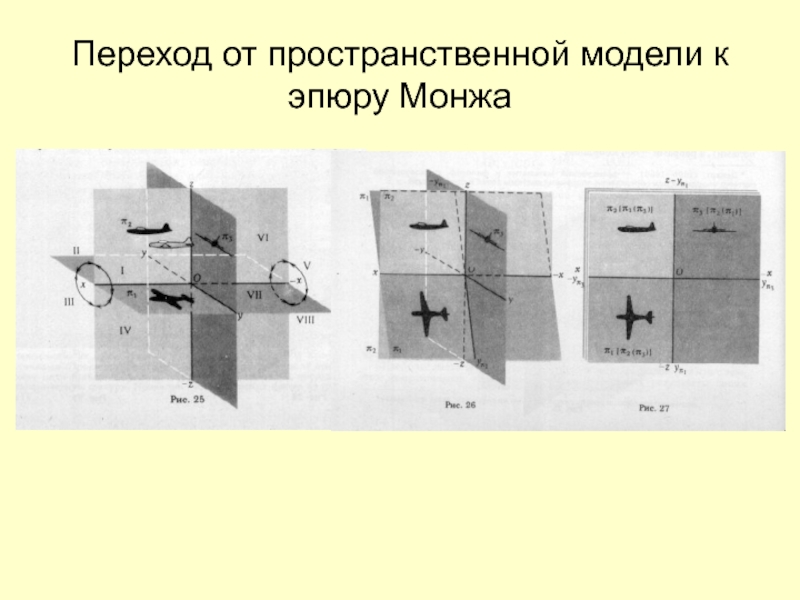
- 11. Переход от пространственной модели к эпюру Монжа
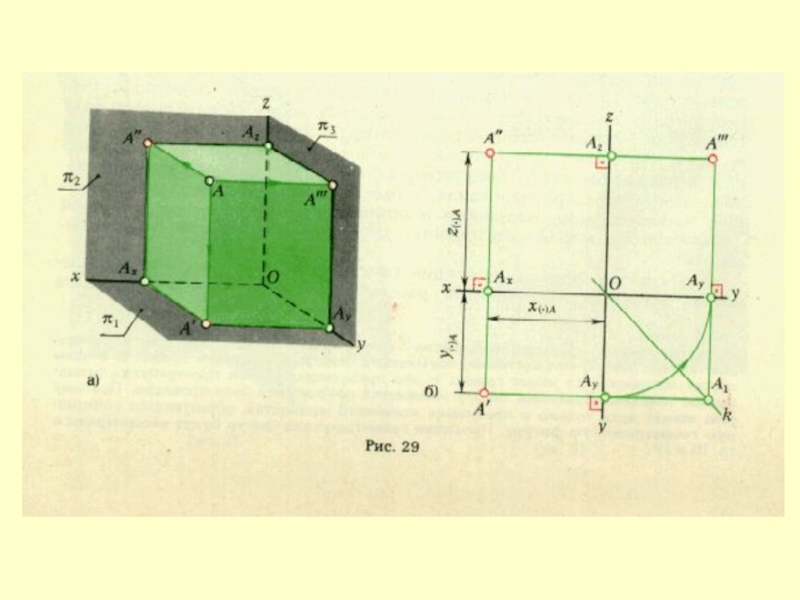
- 12. Слайд 12
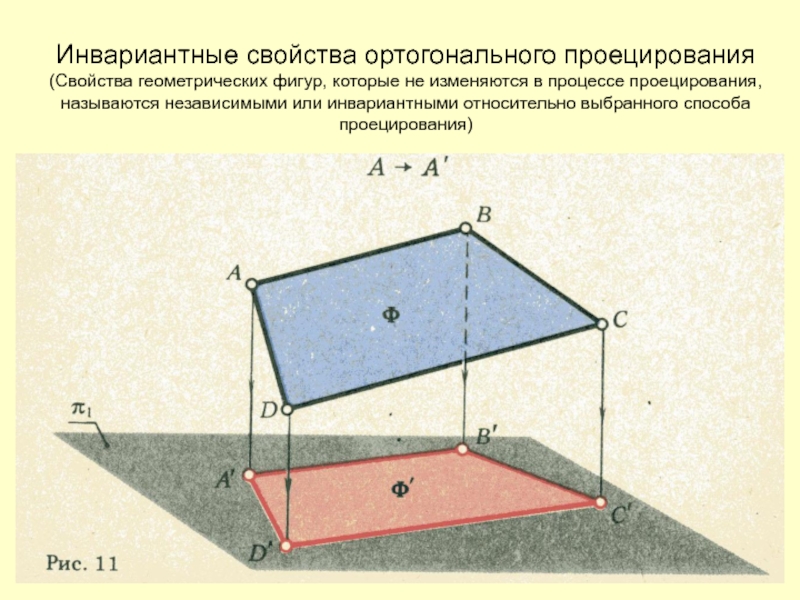
- 13. Инвариантные свойства ортогонального проецирования (Свойства геометрических фигур,
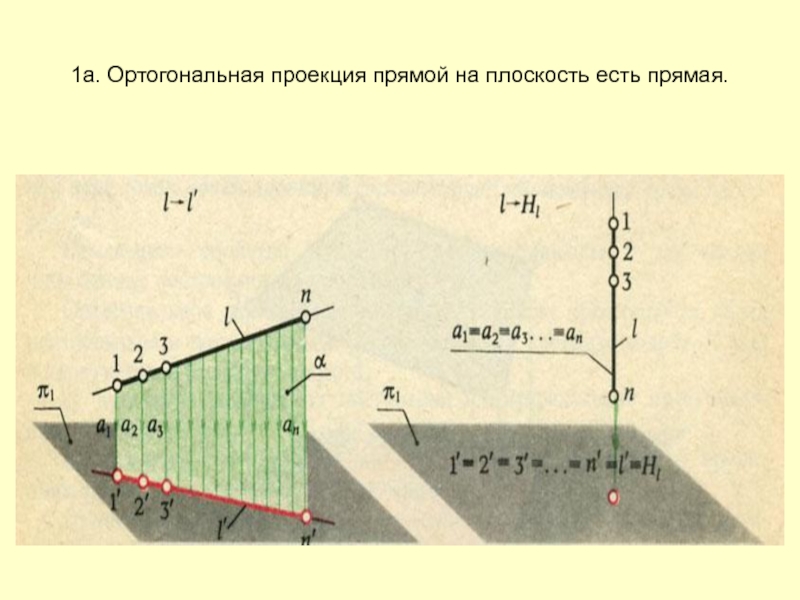
- 14. 1а. Ортогональная проекция прямой на плоскость есть прямая.
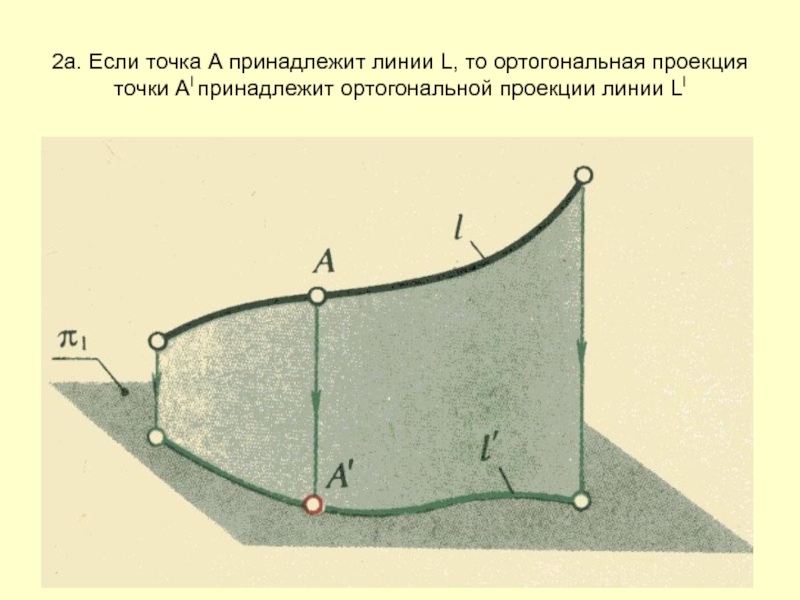
- 15. 2а. Если точка А принадлежит линии L,
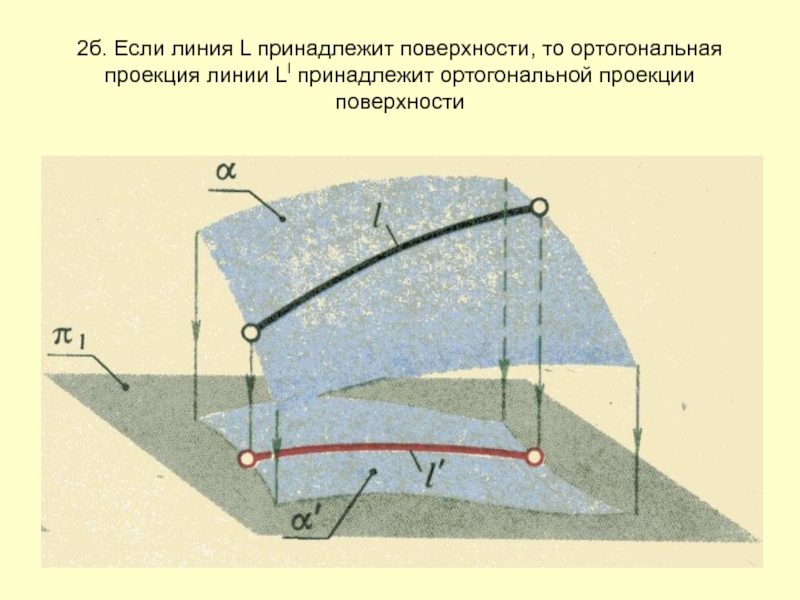
- 16. 2б. Если линия L принадлежит поверхности, то ортогональная проекция линии Ll принадлежит ортогональной проекции поверхности
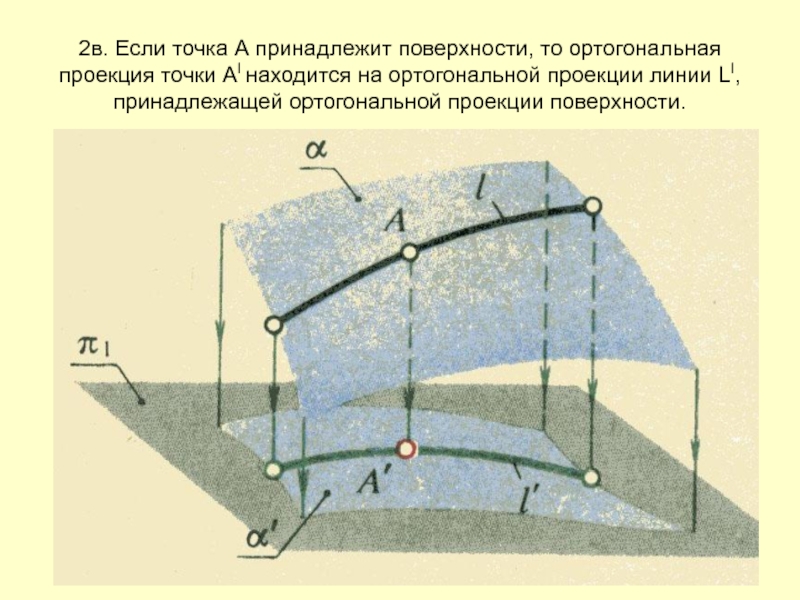
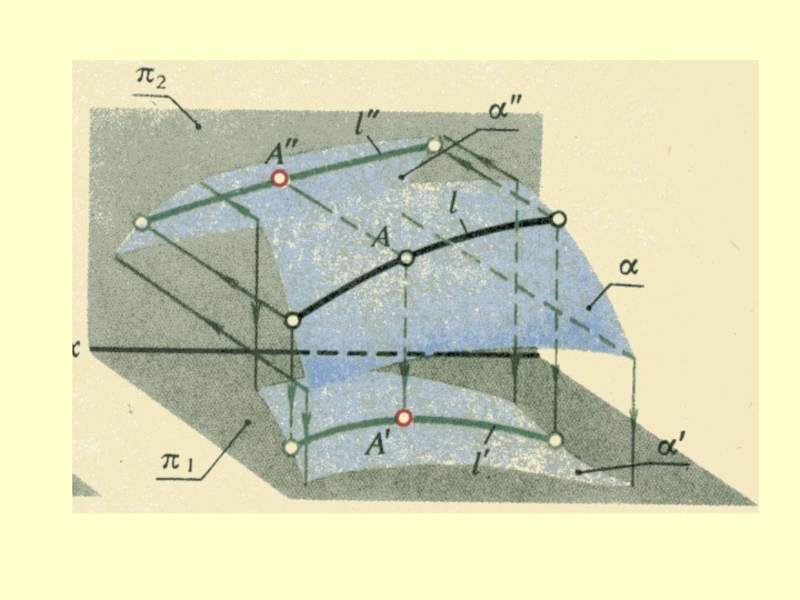
- 17. 2в. Если точка А принадлежит поверхности, то
- 18. Слайд 18
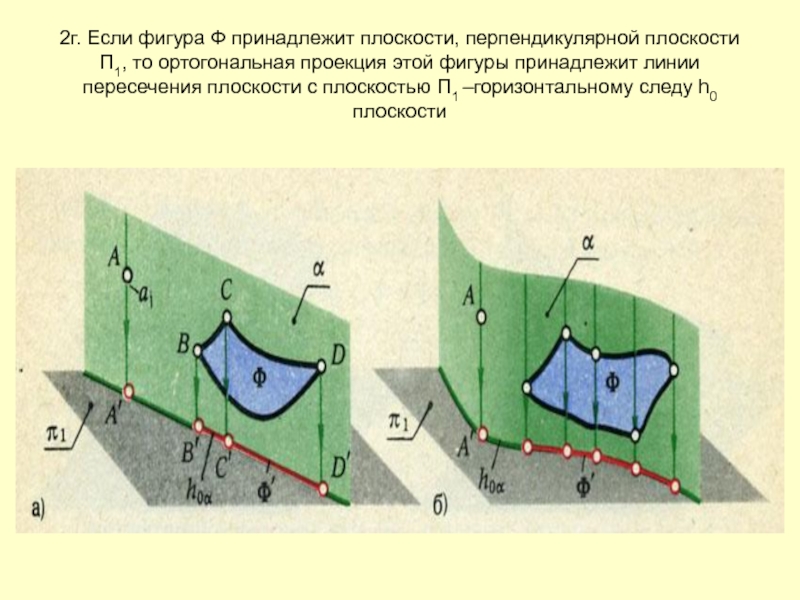
- 19. 2г. Если фигура Ф принадлежит плоскости, перпендикулярной
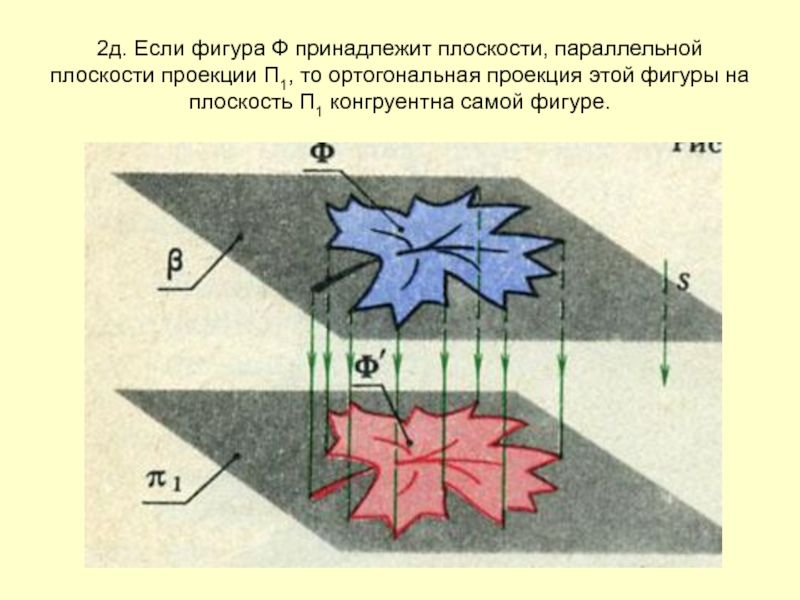
- 20. 2д. Если фигура Ф принадлежит плоскости, параллельной
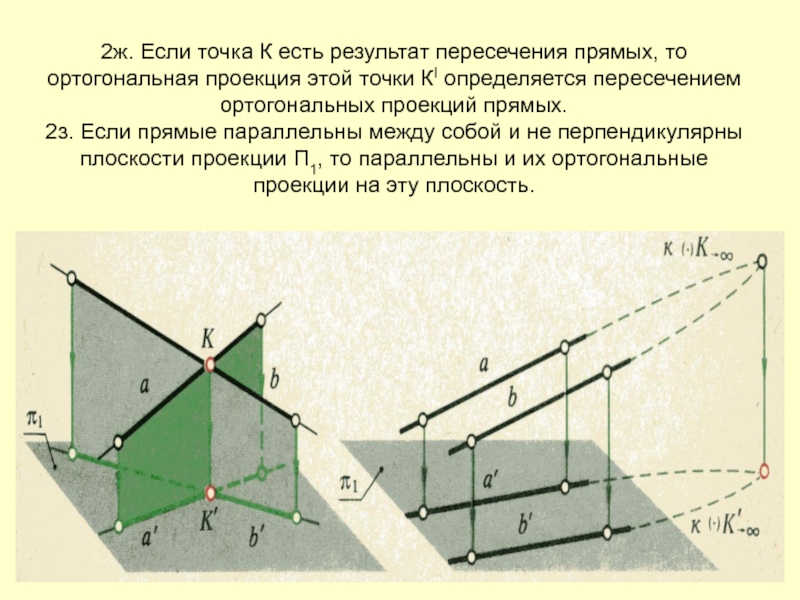
- 21. 2ж. Если точка К есть результат пересечения
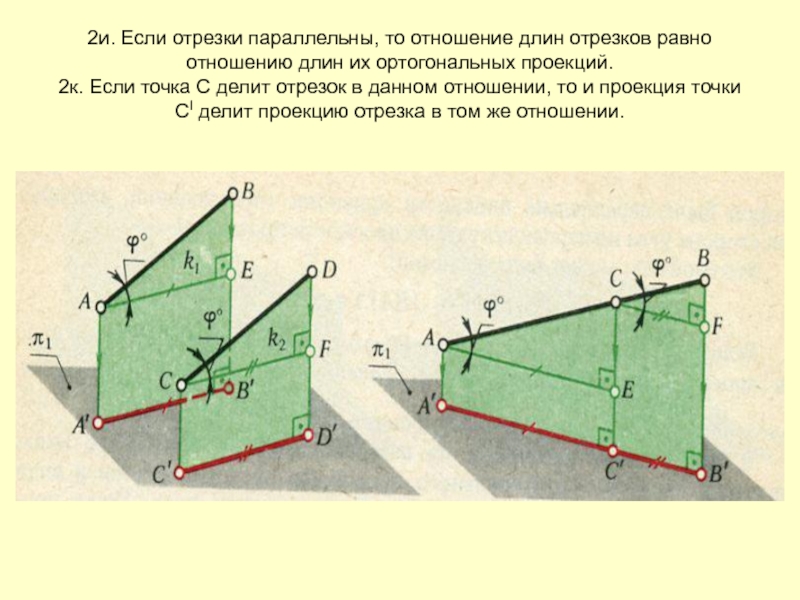
- 22. 2и. Если отрезки параллельны, то отношение длин
- 23. Скачать презентанцию
Кафедра Инженерной и машинной геометрии и графики (О3)Зав. кафедрой: проф. Тихонов-Бугров Д. Е.Дисциплины:«Инженерная графика»«Компьютерная (машинная) графика»«Основы автоматизированного проектирования»Разделы «Инженерной графики»:«Начертательная геометрия»Лектор курса: проф. Абросимов С.Н.«Черчение или стандарты
Слайды и текст этой презентации
Слайд 2Кафедра Инженерной и машинной геометрии и графики
(О3)
Зав. кафедрой: проф. Тихонов-Бугров Д. Е.
Дисциплины:
«Инженерная графика»
«Компьютерная (машинная) графика»
«Основы автоматизированного
проектирования»Разделы «Инженерной графики»:
«Начертательная геометрия»
Лектор курса: проф. Абросимов С.Н.
«Черчение или стандарты ЕСКД»
«Компьютерная графика или компьютерная поддержка инженерной деятельности»
Слайд 3Литература (основная):
1. Фролов С.А. Начертательная геометрия. Учебник для вузов. М.
:Машиностроение.1983.
2. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. Учебное пособие/Под
ред. Ю.Б. Иванова, М. :Наука. Гл. ред. Физ.-мат. Лит. 1988.
3. Арустамов Х.А. Сборник задач по начертательной геометрии. – М. :Машгиз, 1965.
4. Фролов С.А. Сборник задач по начертательной геометрии. Учебное пособие для студентов втузов – М. :Машиностроение, 1980.
Слайд 4Литература (дополнительная):
Бубенников А.В. Начертательная геометрия. – М.: Высшая школа. 1985.
Кузнецов
Н.С. Начертательная геометрия. – М.: Высшая школа. 1981.
Локтев О.В. Краткий
курс начертательной геометрии. – М.: Высшая школа. 1985.Бубенников А.В. Начертательная геометрия – задачи для упражнений. – М.: Высшая школа. 1981.
Локтев О.В., Числов П.А. Задачник по начертательной геометрии. – М.: Высшая школа. 1984.
Слайд 13Инвариантные свойства ортогонального проецирования (Свойства геометрических фигур, которые не изменяются в
процессе проецирования, называются независимыми или инвариантными относительно выбранного способа проецирования)
Слайд 152а. Если точка А принадлежит линии L, то ортогональная проекция
точки Аl принадлежит ортогональной проекции линии Ll
Слайд 162б. Если линия L принадлежит поверхности, то ортогональная проекция линии
Ll принадлежит ортогональной проекции поверхности
Слайд 172в. Если точка А принадлежит поверхности, то ортогональная
проекция точки АI находится на ортогональной проекции линии LI,
принадлежащей ортогональной проекции поверхности.
Слайд 192г. Если фигура Ф принадлежит плоскости, перпендикулярной плоскости П1, то
ортогональная проекция этой фигуры принадлежит линии пересечения плоскости с плоскостью
П1 –горизонтальному следу h0 плоскости
Слайд 202д. Если фигура Ф принадлежит плоскости, параллельной плоскости проекции П1,
то ортогональная проекция этой фигуры на плоскость П1 конгруентна самой
фигуре.
Слайд 212ж. Если точка К есть результат пересечения прямых, то ортогональная
проекция этой точки КI определяется пересечением ортогональных проекций прямых. 2з. Если
прямые параллельны между собой и не перпендикулярны плоскости проекции П1, то параллельны и их ортогональные проекции на эту плоскость.
Слайд 222и. Если отрезки параллельны, то отношение длин отрезков равно отношению
длин их ортогональных проекций. 2к. Если точка С делит отрезок в
данном отношении, то и проекция точки СI делит проекцию отрезка в том же отношении.
