Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Как вычислить определенный интеграл по формуле прямоугольников, трапеций и
Содержание
- 1. Как вычислить определенный интеграл по формуле прямоугольников, трапеций и
- 2. Численные методы – достаточно большой раздел высшей
- 3. Вычисление определенных интегралов по формуле Ньютона-Лейбница не
- 4. Пример: f(x) – непрерывна. Это достаточное условие
- 5. Суть метода прямоугольников Пусть функция y =
- 6. Метод прямоугольниковГде Rn - остаток
- 7. Приведем графическую иллюстрацию метода прямоугольников.Из чертежа видно, что подынтегральная функция y=f(x) приближается кусочной ступенчатой
- 8. С геометрической точки зрения для неотрицательной функции
- 9. Пример решения нестандартным, но достаточно эффективным способом
- 10. Замечание Во многих случаях нахождение наибольшего значения
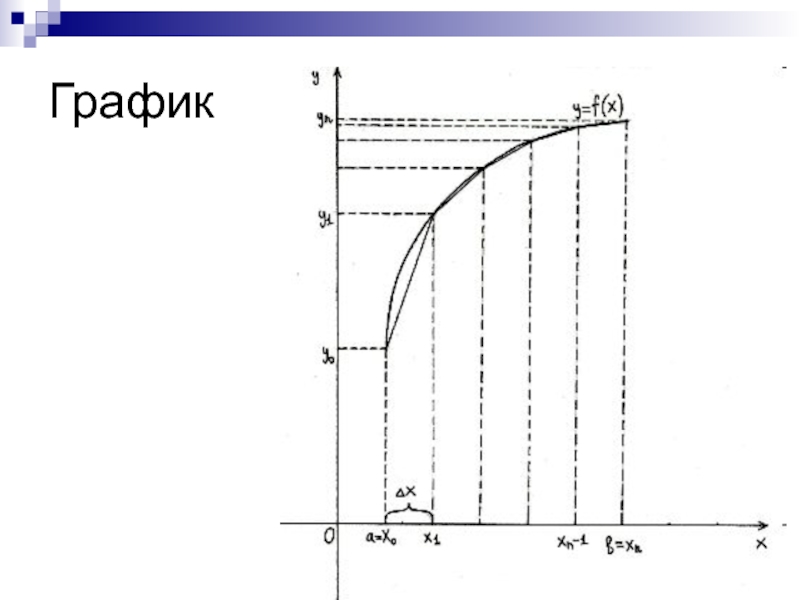
- 11. Метод трапецииМетод трапеций обычно даёт более точное
- 12. График
- 13. Рабочие формулы:Где М2 – максимальное значение из двух производных второго порядка
- 14. Пример решения с помощью Exell решение методом
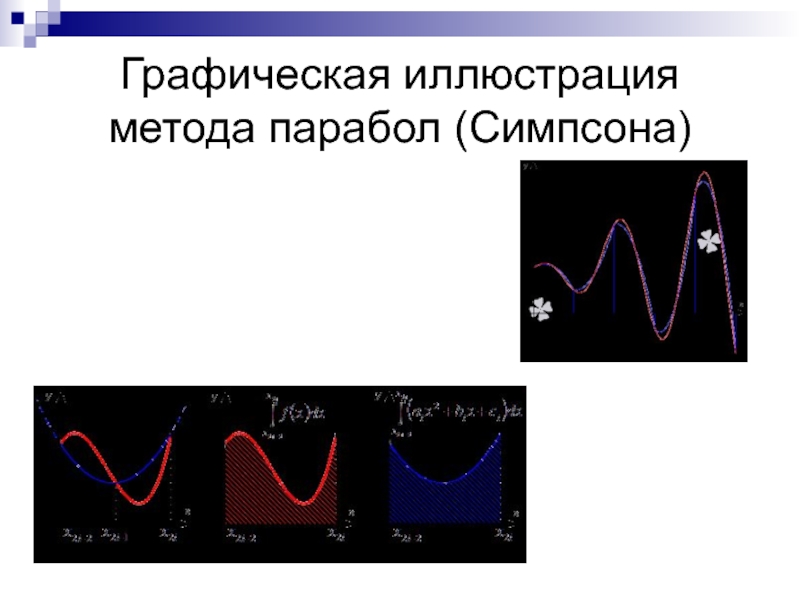
- 15. Метод Симпсона (метод парабол)Это более совершенный
- 16. Расчетные формулыВсе расчеты происходят по одному и тому же алгоритму
- 17. Графическая иллюстрация метода парабол (Симпсона)
- 18. Пример решения с помощью Exell решение методом
- 19. Все производные брались в «ручную» и только
- 20. Спасибо за внимание!
- 21. Скачать презентанцию
Численные методы – достаточно большой раздел высшей математики и серьезные учебники по данной теме насчитывают сотни страниц. На практике, в контрольных работах традиционно предлагаются для решения некоторые задачи по численным методам,
Слайды и текст этой презентации
Слайд 2Численные методы – достаточно большой раздел высшей математики и серьезные
учебники по данной теме насчитывают сотни страниц. На практике, в
контрольных работах традиционно предлагаются для решения некоторые задачи по численным методам, и одной из распространенных задач является – приближенное вычисление определенных интегралов. В этой презентации я рассмотрю три метода приближенного вычисления определенного интеграла – метод прямоугольников, трапеций и метод Симпсона.Что нужно знать, чтобы освоить данные методы? Прозвучит забавно, но можно вообще не уметь брать интегралы. И даже вообще не понимать, что такое интегралы. Из технических средств потребуется микрокалькулятор
Слайд 3Вычисление определенных интегралов по формуле Ньютона-Лейбница не всегда возможно. Многие
подынтегральные функции не имеют первообразных в виде элементарных функций, поэтому
мы во многих случаях не можем найти точное значение определенного интеграла по формуле Ньютона-Лейбница. С другой стороны, точное значение не всегда и нужно. На практике нам часто достаточно знать приближенное значение определенного интеграла с некоторой заданной степенью точности (например, с точностью до одной тысячной). В этих случаях нам на помощь приходят методы численного интегрирования, такие как метод прямоугольников, метод трапеций, метод Симпсона (парабол) и т.п.Слайд 4
Пример: f(x) – непрерывна. Это достаточное условие для дифференцирования функции
на отрезке [a;b].
h= (b-a)/n – шаг, где n – количество
начальных условий.Xk=X0+k*h.
Вычислим интеграл с помощью 3-х следующих методов.
Слайд 5Суть метода прямоугольников
Пусть функция y = f(x) непрерывна на
отрезке [a; b]. Нам требуется вычислить определенный интеграл .
Обратимся к понятию определенного интеграла. Разобьем отрезок [a;b] на n частей точками . Внутри каждого отрезка выберем точку . Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения , то любая из интегральных сумм является приближенным значением интеграла . Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму
Слайд 7Приведем графическую иллюстрацию метода прямоугольников.
Из чертежа видно, что подынтегральная функция
y=f(x) приближается кусочной ступенчатой
Слайд 8С геометрической точки зрения для неотрицательной функции y=f(x) на отрезке
[a;b] точное значение определенного интеграла представляет собой площадь криволинейной трапеции,
а приближенное значение по методу прямоугольников – площадь ступенчатой фигуры.Слайд 9Пример решения нестандартным, но достаточно эффективным способом (с помощью Exell) решение
методом прямоугольников.xls f(x)=п*х/(x+0,2)^2 – проинтегрировать функцию на отрезке от 1 до
2 с шагом в 0,2Слайд 10Замечание
Во многих случаях нахождение наибольшего значения модуля первой производной
(или второй производной для метода средних прямоугольников) подынтегральной функции на
отрезке интегрирования является очень трудоемкой процедурой.Поэтому можно действовать без использования неравенства для оценки абсолютной погрешности методов численного интегрирования.



![Как вычислить определенный интеграл по формуле прямоугольников, трапеций и Пример: f(x) – непрерывна. Это достаточное условие для дифференцирования функции на Пример: f(x) – непрерывна. Это достаточное условие для дифференцирования функции на отрезке [a;b].h= (b-a)/n – шаг, где](/img/thumbs/11fc478bb254ecb351988f191106fee9-800x.jpg)
![Как вычислить определенный интеграл по формуле прямоугольников, трапеций и Суть метода прямоугольников Пусть функция y = f(x) непрерывна на отрезке Суть метода прямоугольников Пусть функция y = f(x) непрерывна на отрезке [a; b]. Нам требуется вычислить определенный](/img/thumbs/58a05fa0be11d87ed63e433cea05664f-800x.jpg)


![Как вычислить определенный интеграл по формуле прямоугольников, трапеций и С геометрической точки зрения для неотрицательной функции y=f(x) на отрезке [a;b] С геометрической точки зрения для неотрицательной функции y=f(x) на отрезке [a;b] точное значение определенного интеграла представляет собой](/img/thumbs/1c31ec39e61f275d7c024823878c5efa-800x.jpg)