Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Коррекция ошибок
Содержание
- 1. Коррекция ошибок
- 2. Категории ошибокНеустранимые {hard failure) Корректируемые (soft errors)
- 3. Неустранимые ошибкивызываются дефектами производственного характера, старением или
- 4. Корректируемые ошибкиносят случайный характер и не являются
- 5. Коррекция ошибокДля нормального функционирования компьютера оба типа
- 6. Организация выявления и исправления ошибок с помощью корректирующего кода
- 7. Слайд 7
- 8. Организация выявления и исправления ошибок с помощью
- 9. Организация выявления и исправления ошибок с помощью
- 10. Организация выявления и исправления ошибок с помощью
- 11. Результат сравненияКоды совпадают, что означает отсутствие ошибок
- 12. Результат сравненияСчитанный информационный и оба дополняющих кода
- 13. Результат сравненияКоды не совпадают, но характер отличия
- 14. Корректирующие коды Дополняющие коды, которые позволяют организовать
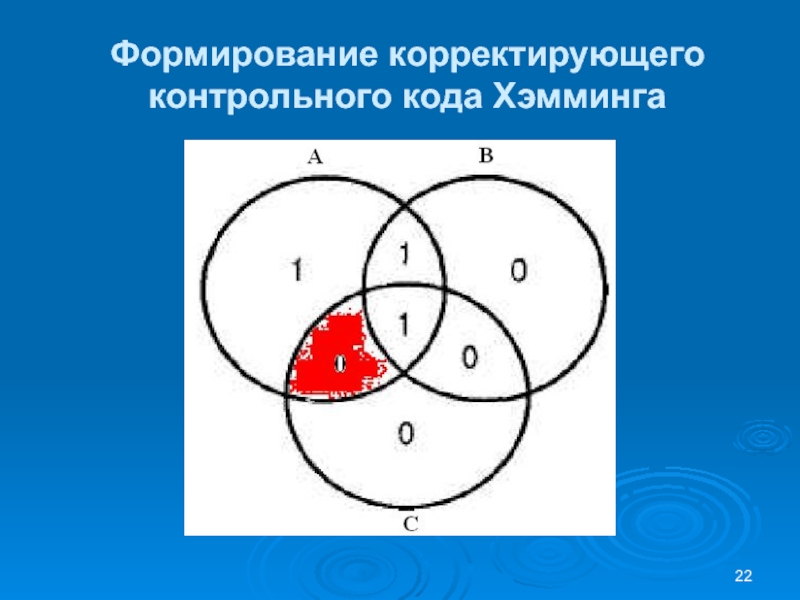
- 15. Формирование корректирующего контрольного кода Хэмминга
- 16. Формирование корректирующего контрольного кода ХэммингаПри пересечении трех
- 17. Формирование корректирующего контрольного кода ХэммингаКаждую из оставшихся
- 18. Формирование корректирующего контрольного кода Хэмминга
- 19. Формирование корректирующего контрольного кода ХэммингаНапример, поскольку круговая
- 20. Формирование корректирующего контрольного кода Хэмминга
- 21. Формирование корректирующего контрольного кода ХэммингаКоличество единиц в
- 22. Формирование корректирующего контрольного кода Хэмминга
- 23. Концепция формирования корректирующего кода ХэммингаНа логическую схему
- 24. Концепция формирования корректирующего кода Хэмминга На выходе
- 25. Концепция формирования корректирующего кода ХэммингаПоскольку ошибка с
- 26. Разрядность корректирующего контрольного кода Хэмминга
- 27. Свойства 4-битового кода признакаВсе биты кода признака
- 28. Свойства 4-битового кода признакаЕсли ошибка содержится в
- 29. Свойства 4-битового кода признакаИнформационные и корректирующие биты
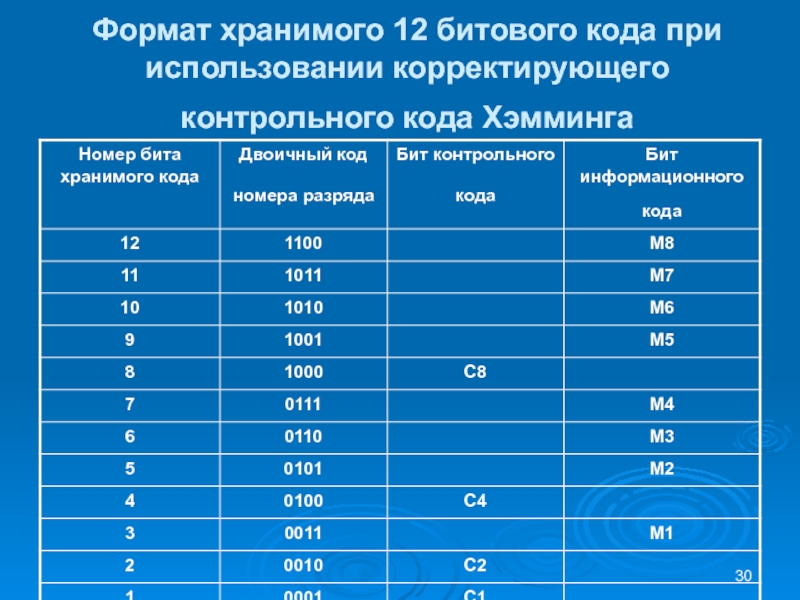
- 30. Формат хранимого 12 битового кода при использовании корректирующего контрольного кода Хэмминга
- 31. Формат хранимого 12 битового кода при использовании
- 32. Контрольный код формируется C1 = M1 ⊕
- 33. Контрольный код формируетсяКаждый бит контрольного кода зависит
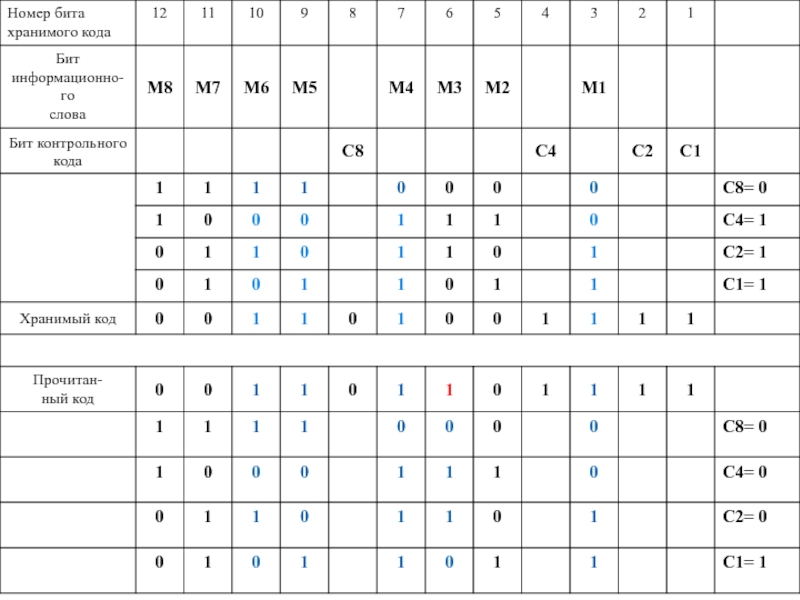
- 34. Пример На входные линии ЗУ подан
- 35. Пример (продолжение) Предположим, что при считывании
- 36. Пример (продолжение) При формировании кода признака на выходе узла сравнения появится код:
- 37. Пример (продолжение)Код 0110 указывает на то, что
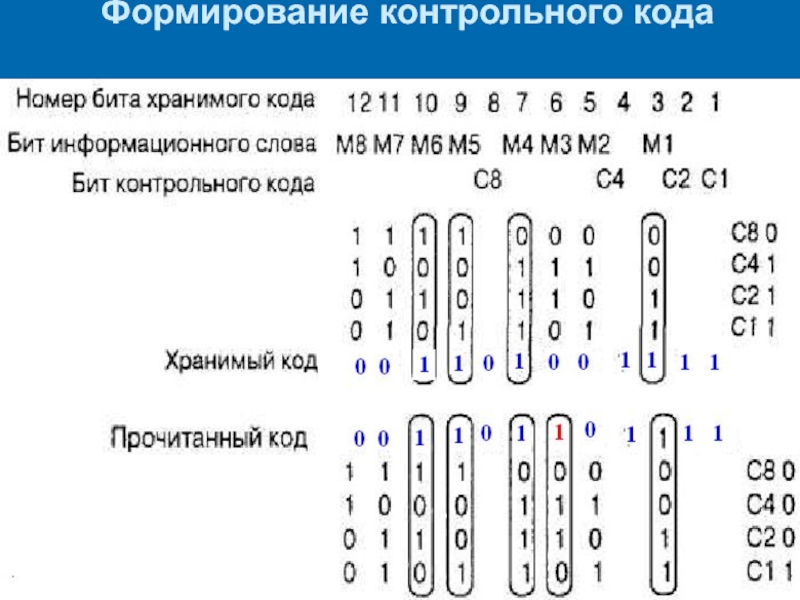
- 38. Формирование контрольного кода
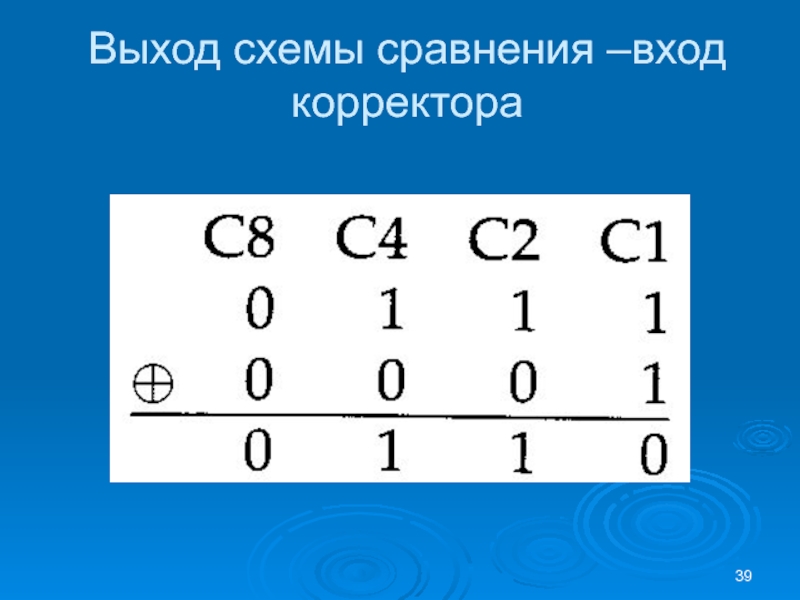
- 39. Выход схемы сравнения –вход корректора
- 40. Слайд 40
- 41. Описанный метод получил название метода коррекции одиночных
- 42. ПрименениеВ современных полупроводниковых ЗУ распространена модификация метода
- 43. ПрименениеИспользование корректирующих кодов повышает надежность работы ЗУ
- 44. ПрименениеНапример, в компьютерах семейства IBM используется 8-битовый
- 45. Скачать презентанцию
Категории ошибокНеустранимые {hard failure) Корректируемые (soft errors)
Слайды и текст этой презентации
Слайд 3Неустранимые ошибки
вызываются дефектами производственного характера, старением или условиями эксплуатации
выражаются
Слайд 4Корректируемые ошибки
носят случайный характер и не являются результатом неисправности модуля
Они могут быть вызваны самыми разными случайными причинами, начиная от
воздействия помех по цепям питания, внешней радиации и кончая температурной нестабильностью работы микросхем 
Слайд 5Коррекция ошибок
Для нормального функционирования компьютера оба типа ошибок представляют серьезную
угрозу и совершенно нежелательны
Поэтому в системе на всех уровнях
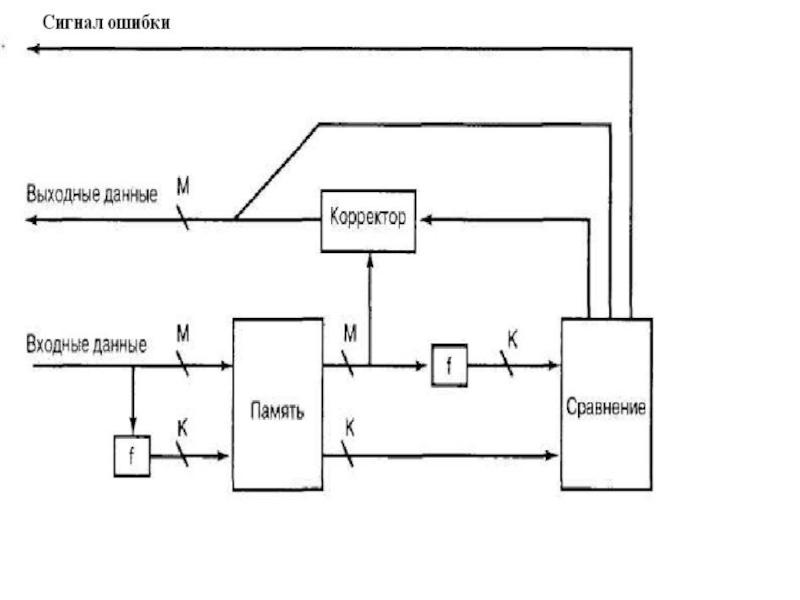
включаются схемы выявления и, если это возможно, коррекции ошибок 
Слайд 8Организация выявления и исправления ошибок с помощью корректирующего кода
Когда поступают
данные, которые требуется сохранить в памяти, они обрабатываются по специальному
алгоритму, обозначенному на схеме как f, и в результате формируется код, дополняющий полученные данныеВ память записывается как "оригинальный" код данных (информационный код), так и сформированный алгоритмом f
Слайд 9Организация выявления и исправления ошибок с помощью корректирующего кода
Если информационный
код состоит из М бит, а дополняющий код — из
К бит, то в ЗУ фактически записывается (М+K) -битовый кодПри чтении данных считывается как информационный код, так и дополняющий
Дополняющий код служит для выявления несоответствия записанного информационного кода и считанного
Слайд 10Организация выявления и исправления ошибок с помощью корректирующего кода
Для этого
информационный код вновь обрабатывается алгоритмом f и формируется дополняющий код
соответственно прочитанному информационномуОба дополняющих кода — прочитанный из памяти (сформированный на этапе записи) и только что сформированный — сравниваются
Слайд 11Результат сравнения
Коды совпадают, что означает отсутствие ошибок в прочитанном информационном
коде. Данные передаются по назначению
Коды не совпадают — значит
прочитанный информационный код отличается от того, который был передан устройству при записиХарактер отличия таков, что ошибка может быть исправлена
Слайд 12Результат сравнения
Считанный информационный и оба дополняющих кода передаются в корректор,
который вносит необходимые исправления в информационный код
После этого исправленный код
данных передается по назначению
Слайд 13Результат сравнения
Коды не совпадают, но характер отличия таков, что ошибка
исправлена быть не может
В этом случае формируется сигнал неустранимой ошибки
Слайд 14Корректирующие коды
Дополняющие коды, которые позволяют организовать коррекцию ошибок описанным
способом называются кодами с исправлением ошибок (error-correcting codes) или корректирующими
кодамиПростейшим корректирующим кодом является код Хэмминга, предложенный Ричардом Хэммингом (Richard Hamming), сотрудником Bell Laboratories
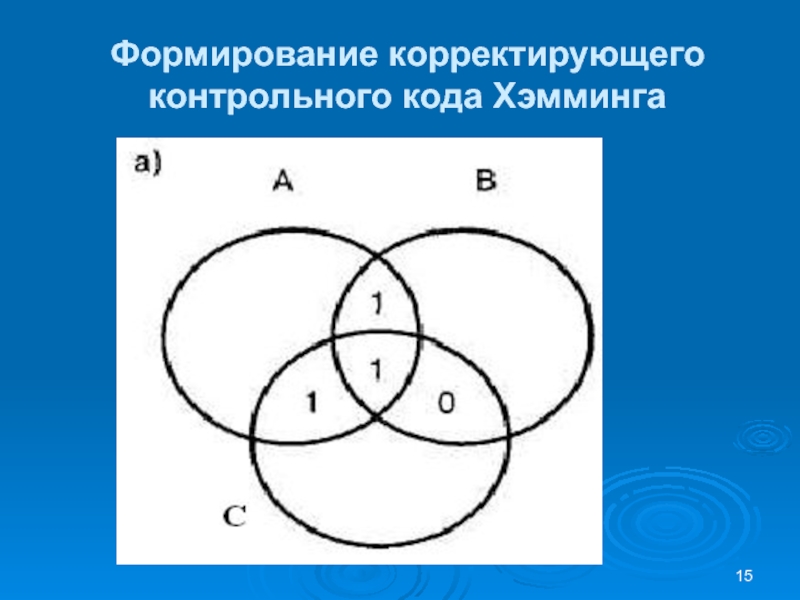
Слайд 16Формирование корректирующего контрольного кода Хэмминга
При пересечении трех круговых областей образуется
семь подобластей, что соответствует семи битам совмещенного (информационный плюс корректирующий)
кодаВнутренним подобластям назначим значения четырех информационных битов
Слайд 17Формирование корректирующего контрольного кода Хэмминга
Каждую из оставшихся подобластей (внешних на
диаграмме) заполним однобитовым кодом контроля четности (parity bit) трехбитового кода
в соседних с ней внутренних подобластяхЗначение кода контроля четности формируется таким образом, чтобы суммарное количество единиц в общем коде было четным
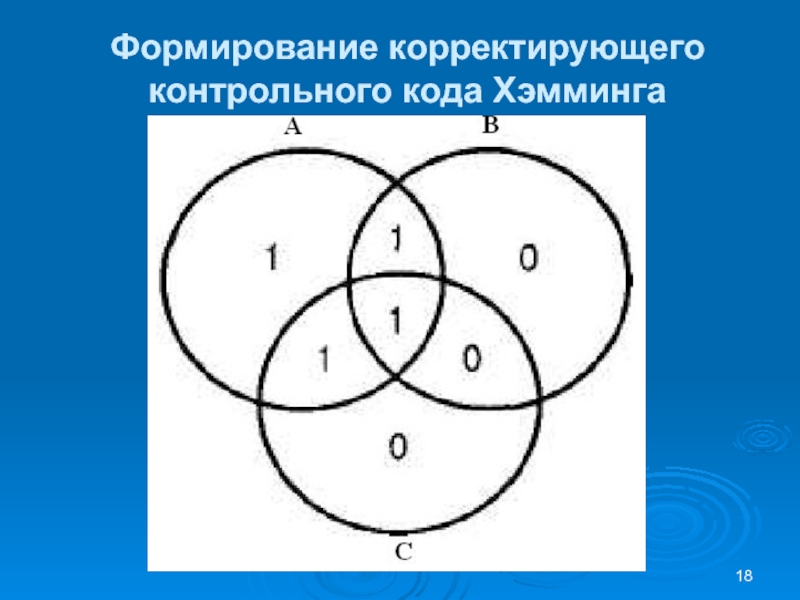
Слайд 19Формирование корректирующего контрольного кода Хэмминга
Например, поскольку круговая область А уже
включает три единицы, то код четности в этой области будет
равен 1 (общее количество единиц тогда будет четным, равным 4)Пусть при считывании один из информационных битов будет искажен
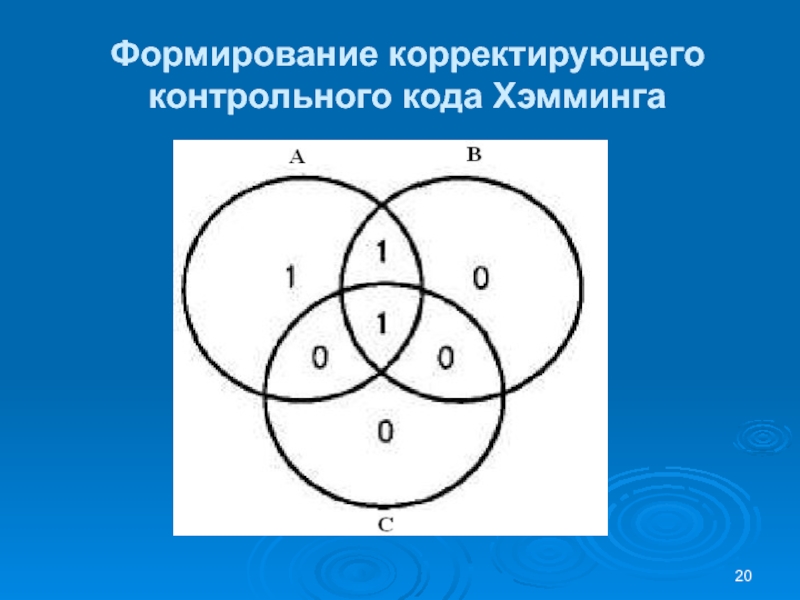
Слайд 21Формирование корректирующего контрольного кода Хэмминга
Количество единиц в круговых областях А
и С нечетно, а в области В — четно
Только
одна из семи подобластей принадлежит областям А и С, но не принадлежит В Следовательно, ошибочным является информационный бит, соответствующий этой подобласти, и его значение следует изменить на противоположное — в данном случае вместо 0 установить 1
Слайд 23Концепция формирования корректирующего кода Хэмминга
На логическую схему сравнения поступают два
K-битовых корректирующих кода
Побитовое сравнение кодов выполняется с помощью логической операции
"исключительное ИЛИ", результат которой равен 0, если сравниваемые коды совпадают 
Слайд 24Концепция формирования корректирующего кода Хэмминга
На выходе узла сравнения образуется
K-битовый код признака, значение которого может быть
в диапазоне от 0 до 2к-1Значение 0 означает, что сравниваемые коды совпадают
Отличные от нуля значения сообщают:
обнаружена ошибка;
какой именно бит считан с ошибкой.
Слайд 25Концепция формирования корректирующего кода Хэмминга
Поскольку ошибка с равной вероятностью может
возникнуть в любом из М информационных и К контрольных битов,
то между параметрами М и K должно соблюдаться соотношение:(2K – 1) > (М + К)
Слайд 27Свойства 4-битового кода признака
Все биты кода признака равны 0, если
ошибка не обнаружена
Если ошибка содержится в одном из четырех контрольных
битов, код признака содержит 1 в одном и только одном битеВ этом случае нет необходимости корректировать информационные биты
Слайд 28Свойства 4-битового кода признака
Если ошибка содержится в информационных битах, числовое
значение кода признака (т.е. значение кода, интерпретируемое как целое число
в двоичной системе счисления) должно указывать номер ошибочного битаКорректор инвертирует двоичный код в этом информационном бите и тем самым исправляет ошибку
Слайд 29Свойства 4-битового кода признака
Информационные и корректирующие биты объединяются в 12-битовый
хранимый код, причем биты каждого типа держатся не компактной группой,
а перемешаны
Слайд 30Формат хранимого 12 битового кода при использовании корректирующего контрольного кода
Хэмминга
Слайд 31Формат хранимого 12 битового кода при использовании корректирующего контрольного кода
Хэмминга
Биты хранимого кода пронумерованы от 1-го до 12-го
Биты, номера
которых представляют собой целую степень числа 2, отводятся для хранения контрольного кода 
Слайд 32Контрольный код формируется
C1 = M1 ⊕ M2 ⊕ M4
⊕ M5 ⊕ M7
C2 = M1 ⊕ M3 ⊕
M4 ⊕ М6 ⊕ M7 C4 = M2 ⊕ МЗ ⊕ M4 ⊕ М8
C8 = M5 ⊕ M6 ⊕ M7 ⊕ М8
Слайд 33Контрольный код формируется
Каждый бит контрольного кода зависит от всех информационных
битов, двоичные номера которых в хранимом коде содержат 1 в
разряде, вес которого совпадает с номером разряда контрольного кода
Слайд 34Пример
На входные линии ЗУ подан 8-битовый код 00111001
(отсчет разрядов в этом коде идет справа налево, т.е. разрядом
Ml считается крайний правый)Биты контрольного кода формируются следующим образом:
С1=1⊕ 0 ⊕ 1⊕ 1⊕ 0=1
С2=1⊕ 0 ⊕ 1⊕ 1⊕ 0=1
С4=0 ⊕ 0 ⊕ 1⊕ 0=1
С8=1⊕ 1 ⊕ 0 ⊕ 0=0
Слайд 35Пример (продолжение)
Предположим, что при считывании в информационном бите
МЗ будет ошибочно прочитан код 1 вместо 0 (00111101)
При повторном формировании контрольного кода по считанным информационным битам будет получено:С1=1⊕0⊕1⊕1⊕0=1
С2=1⊕1⊕1⊕1⊕0=0
С4=0⊕1⊕1⊕0=0
C8=1 ⊕1⊕0⊕0=0
Слайд 37Пример (продолжение)
Код 0110 указывает на то, что в 6-м разряде
считанного хранимого кода (0110=6) обнаружена ошибка и его необходимо инвертировать
Именно в этом разряде хранимого кода содержится информационный бит МЗ
Слайд 41Описанный метод получил название метода коррекции одиночных ошибок, а соответствующий
код — корректирующего кода с исправлением одиночных ошибок (SEC-код —
single-error-correcting code).
Слайд 42Применение
В современных полупроводниковых ЗУ распространена модификация метода формирования контрольного кода,
которая позволяет исправлять одиночные ошибки и выявлять двойные
Такой контрольный код
обозначается аббревиатурой SEC-DED (single-error correction/double-error detection)
Слайд 43Применение
Использование корректирующих кодов повышает надежность работы ЗУ за счет их
усложнения
Если ЗУ состоит из модулей с однобитовой организацией, применение корректирующих
кодов типа SEC-DED рассматривается как вполне адекватная мера обеспечения необходимой надежности
Слайд 44Применение
Например, в компьютерах семейства IBM используется 8-битовый корректирующий код типа
SEC-DED при длине информационного слова оперативной памяти 64 бит
В результате
избыточность ОП по объему составляет примерно 12%
