Курс лекций по теоретической механике

2007
Электронный учебный курс написан на основе лекций, читавшихся автором для

студентов, обучавшихся по специальностям СЖД, ПГС и СДМ в НИИЖТе и МИИТе (1974-2006 гг.). Учебный материал соответствует календарным планам в объеме трех семестров.
Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional.
Замечания и предложения можно послать по e-mail: bond@miit.ru .

Московский государственный университет путей сообщения (МИИТ)
Кафедра теоретической механики
Научно-технический центр транспортных технологий

точки. Основное уравнение динамики. Дифференциальные и естественные уравнения движения. Две

основные задачи динамики. Примеры решения прямой задачи динамики
Лекция 2. Решение обратной задачи динамики. Общие указания к решению обратной задачи динамики. Примеры решения обратной задачи динамики. Движение тела, брошенного под углом к горизонту, без учета сопротивления воздуха.
Лекция 3. Прямолинейные колебания материальной точки. Условие возникновения колебаний. Классификация колебаний. Свободные колебания без учета сил сопротивления. Затухающие колебания. Декремент колебаний.
Лекция 4. Вынужденные колебания материальной точки. Резонанс. Влияние сопротивления движению при вынужденных колебаниях.
Лекция 5. Относительное движение материальной точки. Силы инерции. Частные случаи движения для различных видов переносного движения. Влияние вращения Земли на равновесие и движение тел.
Лекция 6. Динамика механической системы. Механическая система. Внешние и внутренние силы. Центр масс системы. Теорема о движении центра масс. Законы сохранения. Пример решения задачи на использование теоремы о движении центра масс.
Лекция 7. Импульс силы. Количество движения. Теорема об изменении количества движения. Законы сохранения. Теорема Эйлера. Пример решения задачи на использование теоремы об изменении количества движения. Момент количества движения. Теорема об изменении момента количества движения..
Лекция 8. Законы сохранения. Элементы теории моментов инерции. Кинетический момент твердого тела. Дифференциальное уравнение вращения твердого тела. Пример решения задачи на использование теоремы об изменении момента количества движения системы. Элементарная теория гироскопа.

Рекомендуемая литература
1. Яблонский А.А. Курс теоретической механики. Ч.2. М.: Высшая школа. 1977 г. 368 с.
2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с.
3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с.
4. Бондаренко А.Н. “Теоретическая механика в примерах и задачах. Динамика” (электронное пособие www.miit.ru/institut/ipss/faculties/trm/main.htm ), 2004 г.

общей точки
зрения. Движение рассматривается в связи с действующими
на объект силами.

Раздел состоит из трех отделов:

Динамика
материальной точки

Динамика

Динамика
механической системы

Аналитическая механика

■ Динамика точки – изучает движение материальной точки
с учетом сил, вызывающих это движение.
Основной объект - материальная точка – материальное тело, обладающей массой, размерами которого можно пренебречь.

Основные допущения:
– существует абсолютное пространство (обладает чисто геометрическими свойствами, не зависящими от материи и ее движения .
– существует абсолютное время (не зависит от материи и ее движения).
Отсюда вытекает:
– существует абсолютно неподвижная система отсчета.
– время не зависит от движения системы отсчета.
– массы движущихся точек не зависят от движения системы отсчета.
Эти допущения используются в классической механике, созданной Галилеем и Ньютоном. Она имеет до сих пор достаточно широкую область
применения, поскольку рассматриваемые в прикладных науках механические системы не обладают такими большими массами и скоростями
движения, для которых необходим учет их влияния на геометрию пространства, время, движение, как это делается в релятивистской механике
(теории относительности).

■ Основные законы динамики – впервые открытые Галилеем и сформулированные Ньютоном составляют основу всех методов описания и анализа движения механических систем и их динамического взаимодействия под действием различных сил.
■ Закон инерции (закон Галилея-Ньютона) – Изолированная материальная точка тело сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, приложенные силы не заставят ее изменить это состояние. Отсюда следует эквивалентность состояния покоя и движения по инерции (закон относительности Галилея). Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной. Свойство материальной точки стремиться сохранить неизменной скорость своего движения (свое кинематическое состояние) называется инертностью.

■ Закон пропорциональности силы и ускорения (Основное уравнение динамики - II закон Ньютона) – Ускорение, сообщаемое материальной точке силой, прямо пропорционально силе и обратно пропорционально массе этой точки: или

Здесь m – масса точки (мера инертности), измеряется в кг,
численно равна весу, деленному на ускорение свободного падения:

F – действующая сила, измеряется в Н (1 Н сообщает точке массой 1 кг ускорение 1 м/c2, 1 Н = 1/9.81 кг-с).

■ Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами
взаимодействия, с учетом сил, вызывающих это движение.

■ Аналитическая механика – изучает движение несвободных механических систем с использованием общих аналитических методов.

1

уравнение движения точки в векторном виде.
- дифференциальные
уравнения движения
точки в

координатном
виде.

Этот результат может быть получен формальным проецированием векторного дифференциального уравнения (1).

После группировки
векторное соотношение
распадается
на три скалярных
уравнения:

В координатном виде: Используем связь радиуса-вектора с координатами
и вектора силы с проекциями:

или:

Подставим ускорение точки при векторном задании движения в основное уравнение динамики:

Естественные уравнения движения материальной точки – получаются
проецированием векторного дифференциального
уравнения движения на естественные (подвижные)
оси координат: или:

- естественные
уравнения движения
точки.

■ Основное уравнение динамики :

- соответствует векторному способу задания движения точки.

■ Закон независимости действия сил – Ускорение материальной точки под действием нескольких сил равно геометрической сумме ускорений точки от действия каждой из сил в отдельности: или

Закон справедлив для любого кинематического состояния тел. Силы взаимодействия, будучи приложенные к разным точкам (телам)
не уравновешиваются.

■ Закон равенства действия и противодействия (III закон Ньютона) – Всякому действию соответствует равное по величине и противоположно направленное противодействие:

2

траектория). Требуется определить силы, под действием которых происходит заданное движение.
2.

Обратная задача: Заданы силы, под действием которых происходит движение. Требуется найти параметры движения (уравнения движения, траекторию движения).
Обе задачи решаются с помощью основного уравнения динамики и проекции его на координатные оси. Если рассматривается движение несвободной точки, то как и в статике, используется принцип освобождаемости от связей. В результате реакции связей включаются в состав сил, действующих на материальную точку. Решение первой задачи связано с операциями дифференцирования. Решение обратной задачи требует интегрирования соответствующих дифференциальных уравнений и это значительно сложнее, чем дифференцирование. Обратная задача сложнее прямой задачи.

Решение прямой задачи динамики - рассмотрим на примерах:
Пример 1. Кабина весом G лифта поднимается тросом с ускорением a . Определить натяжение троса.

1. Выбираем объект (кабина лифта движется поступательно и ее можно рассматривать как материальную точку).

2. Отбрасываем связь (трос) и заменяем реакцией R.

3. Составляем основное уравнение динамики:

Определяем реакцию троса:

Определяем натяжение троса:

При равномерном движении кабины ay = 0 и натяжение троса равно весу: T = G.
При обрыве троса T = 0 и ускорение кабины равно ускорению свободного падения: ay = -g.

3

4. Проецируем основное уравнение динамики на ось y:

y

Пример 2. Точка массой m движется по горизонтальной поверхности (плоскости Oxy) согласно уравнениям: x = acoskt, y = bcoskt. Определить силу, действующую на точку.

1. Выбираем объект (материальную точку).

2. Отбрасываем связь (плоскость) и заменяем реакцией N.

3. Добавляем к системе сил неизвестную силу F.

4. Составляем основное уравнение динамики:

5. Проецируем основное уравнение динамики на оси x,y :

Определяем проекции силы:

Модуль
силы:

Направляющие косинусы:

Таким образом, величина силы пропорциональна расстоянию точки до центра координат и
направлена к центру по линии, соединяющей точку с центром.
Траектория движения точки представляет собой эллипс с центром в начале координат:

O

r

Лекция 1 (продолжение – 1.3)

тросе длиной l и движется по круговой траектории в горизонтальной

плоскости с некоторой скоростью. Угол отклонения троса от вертикали равен . Определить натяжение троса и скорость груза.

1. Выбираем объект (груз).

2. Отбрасываем связь (трос) и заменяем реакцией R.

3. Составляем основное уравнение динамики:

Из третьего уравнения определяем
реакцию троса:

Определяем натяжение троса:

Подставляем значение реакции
троса, нормального ускорения
во второе уравнение и
определяем скорость груза:

4. Проецируем основное уравнение динамики на оси ,n, b:

Пример 4: Автомашина весом G движется по выпуклому мосту (радиус кривизны равен R) со скоростью V. Определить давление автомашины на мост.

1. Выбираем объект (автомашина, размерами пренебрегаем и рассматриваем как точку).

2. Отбрасываем связь (шероховатую поверхность) и заменяем реакциями N и силой трения Fтр.

3. Составляем основное уравнение динамики:

4. Проецируем основное уравнение динамики на ось n:

Отсюда определяем нормальную реакцию:

Определяем давление автомашины на мост:

Отсюда можно определить скорость, соответствующую нулевому
давлению на мост (Q = 0):

4

одной и той же системы сил
материальная точка может совершать целый

класс движений,
определяемых начальными условиями.
Начальные координаты учитывают исходное положение точки. Начальная скорость, задаваемая проекциями, учитывает влияние на ее движение по рассматриваемому участку траектории сил, действовавших на точку до прихода на этот участок, т.е. начальное кинематическое состояние.

Решение обратной задачи динамики – В общем случае движения точки силы, действующие на точку, являются переменными, зависящими
от времени, координат и скорости. Движение точки описывается системой трех дифференциальных уравнений второго порядка:

После интегрирования
каждого из них будет
шесть постоянных
C1, C2,…., C6:

Значения постоянных C1, C2,…., C6
находятся из шести начальных
условий при t = 0:

Пример 1 решения обратной задачи: Свободная материальная точка массы m движется по действием силы F, постоянной по модулю и величине. . В начальный момент скорость точки составляла v0 и совпадала по направлению с силой. Определить уравнение движение точки.

1. Составляем основное уравнение динамики:

3. Понижаем порядок производной:

2. Выберем декартову систему отсчета, направляя ось x вдоль направления силы
и спроецируем основное уравнение динамики на эту ось: или

x

y

z

4. Разделяем переменные:

5. Вычисляем интегралы от обоих частей уравнения:

6. Представим проекцию скорости
как производную координаты по времени:

8. Вычисляем интегралы от обоих частей уравнения:

7. Разделяем переменные:

9. Для определения значений постоянных C1 и C2 используем начальные условия t = 0, vx = v0 , x = x0 :

В итоге получаем уравнение равнопеременного движения (по оси x):

5

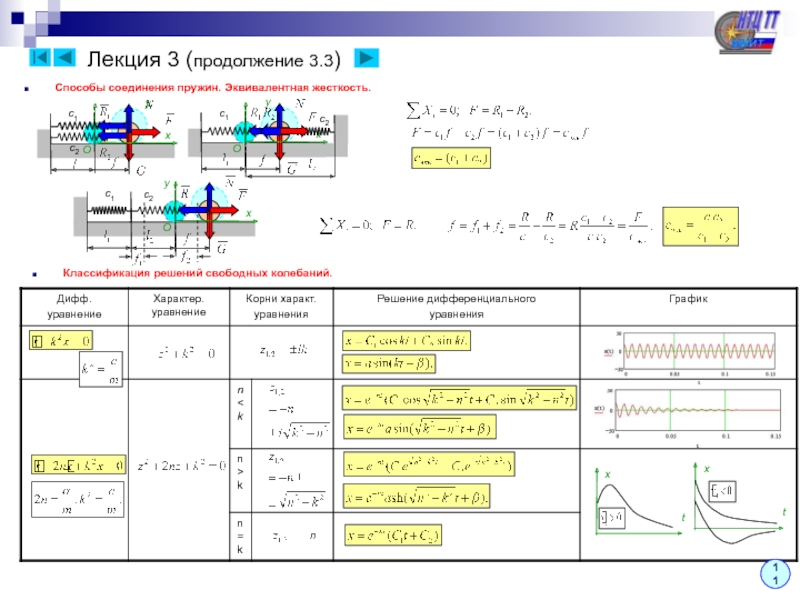
Составление дифференциального уравнения движения:
1.1. Выбрать систему координат – прямоугольную

(неподвижную) при неизвестной траектории движения, естественную (подвижную) при известной траектории, например, окружность или прямая линия. В последнем случае можно использовать одну прямолинейную координату. Начало отсчета совместить с начальным положением точки (при t = 0) или с равновесным положением точки, если оно существует, например, при колебаниях точки.

6

1.2. Изобразить точку в положении, соответствующем произвольному моменту времени (при t > 0) так, чтобы координаты были положительными
(s > 0, x > 0). При этом считаем также, что проекция скорости в этом положении также положительна. В случае колебаний проекция
скорости меняет знак, например, при возвращении к положению равновесия. Здесь следует принять, что в рассматриваемый момент
времени точка удаляется от положения равновесия. Выполнение этой рекомендации важно в дальнейшем при работе с силами
сопротивления, зависящими от скорости.

1.3. Освободить материальную точку от связей, заменить их действие реакциями, добавить активные силы.

1.4. Записать основной закон динамики в векторном виде, спроецировать на выбранные оси, выразить задаваемые или реактивные силы
через переменные время, координаты или скорости, если они от них зависят.

2. Решение дифференциальных уравнений:
2.1. Понизить производную, если уравнение не приводится к каноническому (стандартному) виду. например: или

2.2. Разделить переменные, например: или

2.4. Вычислить неопределенные интегралы в левой и правой частях уравнения, например:

2.3. Если в уравнении три переменных,
то сделать замену переменных, например: и затем разделить переменные.

Замечание. Вместо вычисления неопределенных интегралов можно вычислить определенные интегралы с переменным верхним пределом.
Нижние пределы представляют начальные значения переменных (начальные условия) .Тогда не требуется отдельного нахождения постоянной,
которая автоматически включается в решение, например:

Используя начальные условия, например, t = 0, vx = vx0, определить постоянную интегрирования:

2.5. Выразить скорость через производную координаты по времени, например, и повторить пункты 2.2 -2.4

Замечание. Если уравнение приводится к каноническому виду, имеющему стандартное решение, то это готовое решение и используется.
Постоянные интегрирования по прежнему находятся из начальных условий. См., например, колебания (лекция 4, стр.8).

Лекция 2 (продолжение 2.2)

от времени. Груз весом P начинает двигаться по гладкой горизонтальной

поверхности
под действием силы F, величина которой пропорциональна времени (F = kt). Определить пройденное расстояние грузом за время t.

3. Составляем основное уравнение динамики:

5. Понижаем порядок производной:

4. Проецируем основное уравнение динамики на ось x : или

7

6. Разделяем переменные:

7. Вычисляем интегралы от обоих частей уравнения:

9. Представим проекцию скорости
как производную координаты по времени:

10. Вычисляем интегралы от обоих частей уравнения:

9. Разделяем переменные:

8. Определим значение постоянной C1
из начального условия t = 0, vx = v0=0:

В итоге получаем уравнение движения
(по оси x), которое дает значение
пройденного пути за время t:

1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату:

2. Принимаем объект движения за материальную точку (тело движется поступательно), освобождаем от связи
(опорной плоскости) и заменяем реакцией (нормальной реакцией гладкой поверхности):

11. Определим значение постоянной C2
из начального условия t = 0, x = x0=0:

Пример 3 решения обратной задачи: Сила зависит от координаты. Материальная точка массой m брошена вверх с поверхности Земли со скоростью v0. Сила притяжения Земли обратно пропорциональна квадрату расстояния от точки до центра тяготения (центра Земли). Определить зависимость скорости от расстояния y до центра Земли.

1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату:

2. Составляем основное уравнение динамики:

3. Проецируем основное уравнение динамики на ось y : или

Коэффициент пропорциональности можно найти, используя вес точки на поверхности Земли:

R

Отсюда дифференциальное
уравнение имеет вид: или

4. Понижаем порядок производной:

5. Делаем замену переменной:

6. Разделяем переменные:

7. Вычисляем интегралы
от обоих частей уравнения:

8. Подставляем
пределы:

В итоге получаем выражение
для скорости в функции
от координаты y :

Максимальную высоту
полета можно найти
приравнивая скорость нулю:

Максимальная высота полета 
при обращении знаменателя в нуль:

Отсюда при постановке радиуса Земли и ускорения
свободного падения
получается II космическая
скорость:

от скорости. Судно массы m имело скорость v0. Сопротивление воды

движению судна пропорционально скорости. Определить время, за которое скорость судна упадет вдвое после выключения двигателя, а также пройденное расстояние судном до полной остановки.

8

1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату:

2. Принимаем объект движения за материальную точку (судно движется поступательно), освобождаем от связей
(воды) и заменяем реакцией (выталкивающей силой – силой Архимеда), а также силой сопротивления движению.

3. Добавляем активную силу (силу тяжести).

4. Составляем основное уравнение динамики:

5. Проецируем основное уравнение динамики на ось x : или

6. Понижаем порядок производной:

7. Разделяем переменные:

8. Вычисляем интегралы
от обоих частей уравнения:

9. Подставляем
пределы:

Получено выражение, связывающее скорость и время t, откуда можно определить время движения:

Время движения, за которое
скорость упадет вдвое:

Интересно заметить, что при приближении скорости к нулю время движения стремится к бесконечности, т.е. конечная скорость не может
быть равна нулю. Чем не “вечное движение”? Однако, при этом пройденный путь до остановки является конечной величиной. Для определения пройденного пути обратимся к выражению, полученному после понижения порядка производной, и сделаем замену переменной:

После интегрирования и подстановки пределов получаем:

Пройденный путь
до остановки:

■ Движение точки, брошенной под углом к горизонту, в однородном поле силы тяжести без учета сопротивления воздуха

Исключив время из уравнений движения
получаем уравнение траектории:

Время полета определяем
приравниванием координаты y нулю:

Дальность полета определяем
подстановкой времени полета:

происходит при условии: имеется восстанавливающая сила, стремящая вернуть точку в

положение равновесия при любом отклонении ее из этого положения.

9

Восстанавливающая
сила есть,
положение равновесия
устойчивое

Восстанавливающей
силы нет,
положение равновесия
неустойчивое

Восстанавливающей
силы нет,
положение равновесия
безразличное

Восстанавливающая
сила есть,
положение равновесия
устойчивое

Необходим анализ

Сила упругости пружины – пример линейной восстанавливающей силы.
Направлена всегда к положению равновесия, величина прямо пропорциональна линейному
удлинению (укорочению) пружины, равному отклонению тела от положения равновесия:
с – коэффициент жесткости пружины, численно равный силе, под действием которой пружина изменяет свою длину на единицу, измеряется в Н/м в системе СИ.

x

y

O

Виды колебаний материальной точки:
1. Свободные колебания (без учета сопротивления среды).
2. Свободные колебания с учетом сопротивления среды (затухающие колебания).
3. Вынужденные колебания.
4. Вынужденные колебания с учетом сопротивления среды.

■ Свободные колебания – происходят под действием только восстанавливающей силы.
Запишем основной закон динамики:

Выберем систему координат с центром в положении равновесия (точке O)
и спроецируем уравнение на ось x :

Приведем полученное уравнение
к стандартному (каноническому) виду :

Данное уравнение является однородным линейным дифференциальным
уравнением II порядка, вид решения которого определяется корнями
характеристического уравнения, получаемое с помощью универсальной
подстановки:

Корни характеристического уравнения мнимые и равные:

Общее решение дифференциального
уравнения имеет вид:

Скорость точки:

Начальные условия:

Определим
постоянные:

Итак, уравнение свободных колебаний имеет вид:

Уравнение можно представить
одночленным выражением:

где a – амплитуда,  - начальная фаза.

Новые константы a и  - связаны
с постоянными C1 и C2 соотношениями:

Определим a и  :

Причиной возникновения свободных колебаний является начальное смещение x0 и/или начальная скорость v0.

материальной точки происходит
при наличии восстанавливающей силы и силы сопротивления движению.
Зависимость

силы сопротивления движению от смещения или скорости определяется физической природы
среды или связи, препятствующей движению. Наиболее простой зависимостью является линейная зависимость
от скорости (вязкое сопротивление):

 - коэффициент вязкости

x

y

O

Основное уравнение динамики:

Проекция уравнения динамики на ось:

Приведем уравнение к стандартному виду:

где

Характеристическое уравнение имеет корни:

Общее решение данного дифференциального уравнения имеет различный вид в зависимости от значений корней:

1. n < k – случай малого вязкого сопротивления: - корни комплексные, различные.

или

x = ae-nt

x = -ae-nt

Частота затухающих колебаний:

Период:

T*

Декремент
колебаний:

ai

ai+1

Логарифмический
декремент колебаний:

Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени.

2. n > k – случай большого вязкого сопротивления: - корни действительные, различные.

или

- эти функции апериодические:

3. n = k : - корни действительные, кратные.

эти функции также апериодические:

жесткость.
y
y
11

действует периодически изменяющаяся сила, называемая возмущающей силой.
Возмущающая сила может иметь

различную природу. Например, в частном случае инерционное воздействие неуравновешенной массы m1 вращающегося ротора вызывает гармонически изменяющиеся проекции силы:

Основное уравнение динамики:

Проекция уравнения
динамики на ось:

Приведем уравнение
к стандартному виду:

12

Решение этого неоднородного дифференциального уравнения состоит их двух частей x = x1 + x2 : x1 – общее решение соответствующего
однородного уравнения и x2 – частное решение неоднородного уравнения:

Частное решение подбираем в форме правой части:

Полученное равенство должно удовлетворяться при любом t .

Тогда: или

Таким образом, при одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат сложения (наложения) свободных (x1) и вынужденных (x2) колебаний.
Если p < k (вынужденные колебания малой частоты),
то фаза колебаний совпадает с фазой возмущающей силы:

В итоге полное решение: или

Общее решение:

Постоянные С1 и С2, или a и  определяются из начальных условий с использованием полного решения (!):

Таким образом, частное решение:

Если p > k (вынужденные колебания большой частоты),
то фаза колебаний противоположна фазе возмущающей силы:

статическому отклонению точки под действием постоянной силы H = const:
Амплитуда
вынужденных

колебаний:

Статическое отклонение можно найти из уравнения равновесия:
Здесь:

Отсюда:

Таким образом, при p < k
(малая частота
вынужденных колебаний)
коэффициент динамичности:

При p > k
(большая частота
вынужденных колебаний)
коэффициент динамичности:

Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках.
Дифференциальное уравнение колебаний при равенстве частот:

Частное решение в форме правой части взять нельзя, т.к. получится линейно зависимое решение (см. общее решение).

Общее решение:

Подставим в дифференциальное
уравнение:

Возьмем частное решение в виде и вычислим производные :

Таким образом, получено решение: или

Вынужденные колебания при резонансе имеют амплитуду неограниченно возрастающую пропорционально времени.

Влияние сопротивления движению при вынужденных колебаниях.
Дифференциальное уравнение при наличии вязкого сопротивления имеет вид:

Общее решение выбирается из таблицы (Лекция 3, стр. 11) в зависимости от соотношения n и к (посмотреть).

Частное решение возьмем в виде и вычислим производные :

Подставим в дифференциальное уравнение:

Приравнивая коэффициенты при одинаковых тригонометрических функциях получаем систему уравнений:

Возведением в степень обоих
уравнений и сложением их
получаем амплитуду
вынужденных колебаний:

Делением второго уравнения
на первое получаем сдвиг фазы вынужденных колебаний:

Таким образом, уравнение движения при вынужденных колебаний с учетом сопротивления движению, например при n < k (малое сопротивление):

Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения
возмущающей силы. Коэффициент динамичности при резонансе имеет
конечную величину и зависит от соотношения n и к.

система координат Oxyz движется по некоторому закону относительно неподвижной (инерциальной)

системы координат O1x1y1z1. Движение материальной точки M (x, y, z) относительно подвижной системы Oxyz– относительное, относительно неподвижной системы O1x1y1z1– абсолютное. Движение подвижной системы Oxyz относительно неподвижной системы O1x1y1z1– переносное движение.

14

z

x1

y1

z1

O1

x

y

M

x

y

z

O

Основное уравнение динамики:

Абсолютное ускорение точки:

Подставим абсолютное ускорение точки в основное уравнение динамики:

Перенесем слагаемые с переносным и кориолисовым ускорением в правую часть:

Перенесенные слагаемые имеют
размерность сил и рассматриваются
как соответствующие силы инерции,
равные:

Тогда относительное движение точки можно рассматривать как абсолютное, если к действующим силам добавить переносную и кориолисову силы инерции:

В проекциях на оси подвижной системы
координат имеем:

Частные случаи относительного движения точки для различного вида переносного движения:

1. Вращение вокруг неподвижной оси:

Если вращение
равномерное, то εe = 0:

2. Поступательное криволинейное движение:

Если движение прямолинейное, то  = :

Если движение прямолинейное и равномерное, то подвижная система является инерциальной и относительное движение может рассматриваться как абсолютное: Никакими механическими явлениями нельзя обнаружить прямолинейного равномерного движения (принцип относительности классической механики).

Влияние вращения Земли на равновесие тел – Положим, что тело находится в равновесии на поверхности Земли на произвольной широте φ (параллели). Земля вращается вокруг своей оси с запада на восток с угловой скоростью: Радиус Земли составляет около 6370 км.

S

R – полная реакция негладкой поверхности.

G – сила притяжения Земли к центру.

Ф – центробежная сила инерции.

Условие относительного равновесия:

Равнодействующая сил притяжения и инерции – сила тяжести (вес):

Величина силы тяжести (веса) на поверхности Земли равна P = mg .
Центробежная сила инерции составляет малую долю от силы тяжести:

Отклонение силы тяжести
от направления силы притяжения также мало :

Таким образом, влияние вращения Земли на равновесие тел чрезвычайно мало и в практических расчетах не принимается во внимание.

Максимальная величина силы инерции (при φ = 0 - на экваторе) составляет всего 0.00343 от величины силы тяжести

поле тяготения Земли – Положим тело падает на Землю с

некоторой высоты H над поверхностью Земли на широте φ . Выберем подвижную систему отсчета, жестко связанную с Землей, направляя оси x, y по касательной к параллели и к меридиану:

Уравнение относительного движения:

Здесь учтена малость центробежной силы инерции по сравнению с силой тяжести. Таким образом сила
тяготения отождествляется с силой тяжести. Кроме того, считаем, что сила тяжести направлена перпендикулярно поверхности Земли вследствие малости ее отклонения, как рассмотрено выше.

Ускорение Кориолиса равно и направлено параллельно оси y на запад.

Сила инерции Кориолиса равна направлена в противоположную сторону.

Спроецируем уравнение относительного движения на оси:

Решение первого уравнения дает:

Начальные условия:

Решение третьего уравнения дает:

Начальные условия:

Третье уравнение принимает вид:

Начальные условия:

Его решение дает:

Полученное решение показывает, что тело при падении отклоняется к востоку.
Вычислим величину этого отклонения, например, при падении с высоты 100 м.
Время падения найдем
из решения второго уравнения:

Таким образом, влияние вращения Земли на движение тел
чрезвычайно мало для практических высот и скоростей и
в технических расчетах не учитывается.
Из решения второго уравнения также следует существование
скорости по оси y, которая также должна вызывать и вызывает
соответствующее ускорение и силу инерции Кориолиса.
Влияние этой скорости и силы инерции, связанной с ней,
на изменение движения будет еще меньше, чем
рассмотренная сила инерции Кориолиса, связанная с
вертикальной скоростью.

Совокупность материальных точек или материальных тех, объединяемых общими законами взаимодействия

(положение или движение каждой из точек или тела зависит от положения и движения всех остальных)
Система свободных точек - движение которых не ограничивается никакими связями (например, планетная система, в которой планеты рассматриваются как материальные точки).
Система несвободных точек или несвободная механическая система – движение материальных точек или тел ограничиваются наложенными на систему связями (например, механизм, машина и т.п.).

16

Силы, действующие на систему. В дополнение к ранее существовавшей классификации сил (активные и реактивные силы) вводится новая
классификация сил:
1. Внешние силы (e) – действующие на точки и тела системы со стороны точек или тел, не входящих в состав данной системы.
2. Внутренние силы (i) – силы взаимодействия между материальными точками или телами, входящими в данную систему.
Одна и та же сила может являться как внешней, так и внутренней силой. Все зависит от того, какая механическая система рассматривается.
Например: В системе Солнце, Земля и Луна все силы тяготения между ними являются внутренними. При рассмотрении системы Земля и Луна силы
тяготения, приложенные со стороны Солнца – внешние:

C

З

Л

На основании закона действия и противодействия каждой внутренней силе Fk соответствует другая внутренняя
сила Fk’, равная по модулю и противоположная по направлению.

Из этого следуют два замечательных свойства внутренних сил:
Главный вектор всех внутренних сил системы равен нулю:

Главный момент всех внутренних сил системы относительно
любого центра равен нулю:

Или в проекциях на координатные оси:

Замечание. Хотя эти уравнения похожи на уравнения равновесия, они таковыми не являются, поскольку внутренние силы приложены к различным точкам или телам системы и могут вызывать движение этих точек (тел) относительно друг друга. Из этих уравнений следует,
что внутренние силы не влияют на движение системы, рассматриваемой как одно целое.

Центр масс системы материальных точек. Для описания движения системы в целом вводится
геометрическая точка, называемой центром масс, радиус-вектор которой определяется
выражением , где M – масса всей системы:

Или в проекциях на координатные оси:

Формулы для центра масс аналогичны формулам для центра тяжести. Однако, понятие центра масс более общее, поскольку оно не связано с силами тяготения или силами тяжести.

Рассмотрим систему n материальных точек. Приложенные к каждой точке силы

разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или

Просуммируем эти уравнения
по всем точкам:

В левой части уравнения внесем массы под знак производной
и заменим сумму производных на производную суммы:

Из определения центра масс:

Подставим в полученное уравнение:

После вынесения массы системы
за знак производной получаем или:

Произведение массы системы на ускорение ее центра массе равно главному вектору внешних сил.

В проекциях на координатные оси:

Центр масс системы движется как материальная точка массой, равной массе
всей системы, к которой приложены все внешние силы, действующие на систему.

Следствия из теоремы о движении центра масс системы
(законы сохранения):
1. Если в интервале времени [t1, t2] главный вектор внешних сил системы
равен нулю, Re = 0, то скорость центра масс постоянна, vC = const
(центр масс движется равномерно прямолинейно – закон сохранения
движения центра масс).
2. Если в интервале времени [t1, t2] проекция главного вектора внешних сил
системы на ось x равна нулю, Rxe = 0, то скорость центра масс по оси x
постоянна, vCx = const (центр масс движется по оси равномерно).
Аналогичные утверждения справедливы для осей y и z.

Пример: Два человека массами m1 и m2 находятся в лодке массой m3.
В начальный момент времени лодка с людьми находилась в покое.
Определить перемещение лодки, если человек массой m2 пересел к носу лодки на расстояние а.

3. Если в интервале времени [t1, t2] главный вектор внешних сил системы
равен нулю, Re = 0, и в начальный момент скорость центра масс равна нулю,
vC = 0, то радиус-вектор центра масс остается постоянным, rC = const (центр
масс находится в покое – закон сохранения положения центра масс).
4. Если в интервале времени [t1, t2] проекция главного вектора внешних сил
системы на ось x равна нулю, Rxe = 0, и в начальный момент скорость центра
масс по этой оси равна нулю, vCx = 0, то координата центра масс по оси x
остается постоянной, xC = const (центр масс не движется по этой оси).
Аналогичные утверждения справедливы для осей y и z.

1. Объект движения (лодка с людьми):

2. Отбрасываем связи (воду):

3. Заменяем связь реакцией:

4. Добавляем активные силы:

5. Записываем теорему о центре масс:

Проецируем на ось x :

O

Определим на какое расстояние надо пересесть человеку массы m1, чтобы лодка осталась на месте:

Лодка переместится на расстояние l в противоположную сторону.

движения со стороны действующих на точку сил за данный промежуток

времени:

18

В проекциях
на координатные оси:

В случае постоянной силы:

В проекциях на координатные оси:

Импульс равнодействующей – равен геометрической сумме импульсов приложенных к точке сил за один и тот же промежуток времени:

Умножим на dt:

Проинтегрируем на данном промежутке времени:

Количество движения точки – мера механического движения, определяемая вектором, равным произведению массы точки на вектор ее скорости:

Теорема об изменении количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или

Количество движения системы материальных точек – геометрическая сумма количеств движения материальных точек:

По определению центра масс:

Вектор количества движения системы равен произведению
массы всей системы на вектор скорости центра масс системы.

Тогда:

В проекциях на координатные оси:

Производная вектора количества движения системы по времени равна главному вектору внешних сил системы.

Просуммируем эти уравнения
по всем точкам:

В левой части уравнения внесем массы под знак производной
и заменим сумму производных на производную суммы:

Из определения количества движения системы:

В проекциях
на координатные оси:

к движению сплошной среды (воды) .
1.Выбираем в качестве объекта движения

объем воды, находящийся в криволинейном канале турбины:

2. Отбрасываем связи и заменяем их действие реакциями (Rпов – равнодействующая поверхностных сил)

3. Добавляем активные силы (Rоб – равнодействующая объемных сил):

4. Записываем теорему об изменении количества движения системы:

Количество движения воды в моменты времени t0 и t1
представим как суммы:

Изменение количества движения воды в интервале времени [t0,t1] :

Изменение количества движения воды
за бесконечно малый интервал времени dt: , где

F1

F2

Принимая произведение плотности, площади поперечного сечения и скорости за секундную массу
получаем:

Подставляя дифференциал количества движения системы
в теорему об изменении получаем:

Следствия из теоремы об изменении количества движения системы
(законы сохранения):
1. Если в интервале времени [t1, t2] главный вектор внешних сил системы
равен нулю, Re = 0, то вектор количества движения постоянен, Q = const
– закон сохранения количества движения системы).
2. Если в интервале времени [t1, t2] проекция главного вектора внешних сил
системы на ось x равна нулю, Rxe = 0, то проекция количества движения
системы на ось x постоянна, Qx = const.
Аналогичные утверждения справедливы для осей y и z.

Лекция 7 (продолжение 7.2)

Пример: Граната массы M, летевшая со скоростью v, разорвалась на две части. Скорость одного из осколков массы m1 возросла в направлении движения до величины v1. Определить скорость второго осколка.

1. Объект движения (граната):

2. Объект – свободная система,
связи и их реакции отсутствуют.

3. Добавляем активные силы:

4. Записываем теорему об изменении количества движения:

Проецируем на ось  :



β

Разделяем переменные и интегрируем :

Правый интеграл практически равен нулю, т.к. время взрыва t<<1.

Отсюда закон сохранения :

Геометрическая разность векторов секундных количеств движения жидкости равна
сумме главных векторов объемных и поверхностных сил.

19

В проекциях на оси:

Разность проекций векторов секундных количеств движения жидкости на ось равна
сумме проекций главных векторов объемных и поверхностных сил на ту же ось.

движения относительно некоторого центра – мера механического движения, определяемая вектором,

равным векторному произведению радиуса-вектора материальной точки на вектор ее количества движения:

Кинетический момент системы
материальных точек относительно
некоторого центра – геометрическая
сумма моментов количеств движений
всех материальных точек относительно
этого же центра:

В проекциях на оси:

В проекциях на оси:

Теорема об изменении момента количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или

Просуммируем эти уравнения
по всем точкам:

Заменим сумму производных
на производную суммы:

Выражение в скобках есть момент количества движения системы. Отсюда:

Умножим векторно каждое из равенств на радиус-вектор слева:

Посмотрим, можно ли вынести знак производной
за пределы векторного произведения:

Таким образом, получили:

Производная вектора момента количества движения системы относительно некоторого центра по времени равна главному моменту внешних сил системы относительно этого же центра.

В проекциях
на координатные оси:

Производная момента количества движения системы относительно некоторой оси по времени равна главному моменту внешних сил системы относительно этой же оси.

момента количества движения системы (законы сохранения):
1. Если в интервале времени

[t1, t2] вектор главного момента внешних сил системы относительно некоторого центра равен нулю, MOe = 0, то вектор момента количества движения системы относительно этого же центра постоянен, KO = const – закон сохранения момента количества движения системы).
2. Если в интервале времени [t1, t2] главный момент внешних сил системы относительно оси x равен нулю, Mxe = 0, то момент количества движения системы относительно оси x постоянен, Kx = const.
Аналогичные утверждения справедливы для осей y и z.

2. Момент инерции твердого тела относительно оси:

Момент инерции материальной
точки относительно оси равен
произведению массы точки на
квадрат расстояния точки до оси.

Момент инерции твердого тела относительно оси равен сумме произведений массы каждой точки на квадрат расстояния этой точки до оси.

■ Элементы теории моментов инерции – При вращательном движении твердого тела мерой инерции (сопротивления изменению движения) является момент инерции относительно оси вращения. Рассмотрим основные понятия определения и способы вычисления моментов инерции.
1. Момент инерции материальной точки относительно оси:

При переходе от дискретной малой массы
к бесконечно малой массе точки предел
такой суммы определяется интегралом:

осевой момент инерции
твердого тела.

Кроме осевого момента инерции твердого тела
существуют другие виды моментов инерции:

центробежный момент инерции твердого тела.

полярный момент инерции
твердого тела.

3. Теорема о моментах инерции твердого тела относительно параллельных осей – формула перехода к параллельным осям:

Момент инерции относительно исходной оси

Статические моменты инерции
относительно исходных осей

Масса тела

Расстояние между
осями z1 и z2

Таким образом:

Если ось z1 проходит через центр масс,
то статические моменты равны нулю:

элементарный
объем dV = Adx
на расстоянии x:
x
dx
Элементарная
масса:
Для вычисления момента

инерции относительно центральной
оси (проходящей через центр тяжести) достаточно изменить
расположение оси и задать пределы интегрирования (-L/2, L/2).
Здесь продемонстрируем формулу перехода к параллельным
осям:

zС

5. Момент инерции однородного сплошного цилиндра относительно оси симметрии:

H

dr

r

Выделим элементарный
объем dV = 2πrdrH
(тонкий цилиндр радиуса r) :

Элементарная
масса:

Здесь использована формула объема цилиндра V=πR2H.
Для вычисления момента инерции пустотелого (толстого) цилиндра
достаточно задать пределы интегрирования от R1 до R2 (R2> R1):

6. Момент инерции тонкого цилиндра относительно оси симметрии ( t <

H

C

В силу малости толщины цилиндра
считаем, что все точки находятся
на одинаковом расстоянии R до оси
и интегрирования не требуется.
Объем V = 2πRtH. (тонкий цилиндр
радиуса R с толщиной стенки t).

То же самое можно получить с использованием формулы для толстостенного цилиндра, учитывая малость t:

Поскольку высота цилиндров в результате не входит в формулы моментов инерции, то они остаются справедливыми для тонкого сплошного диска и обода колеса (тонкого кольца).

■ Кинетический момент твердого тела

Выделим дискретный малый объем массы mi :

Или переходя к бесконечно малым:

Кинетический момент вращающегося тела равен произведению угловой скорости на момент инерции относительно оси вращения.

теорему об изменении кинетического момента
твердого тела, вращающегося вокруг неподвижной оси:

Кинетический момент вращающегося твердого тела
равен:

Момент внешних сил относительно оси вращения
равен вращающему моменту (реакции и сила тяжести
моментов не создают):

Подставляем кинетический момент и вращающий момент в теорему

Пример: Два человека одинакового веса G1 = G2 висят на канате, переброшенном через сплошной блок весом G3 = G1/4. В некоторый момент один из них начал подниматься по канату с относительной скоростью u. Определить скорости подъема каждого из людей.

1. Выбираем объект движения (блок с людьми):

2. Отбрасываем связи (опорное устройство блока):

3. Заменяем связь реакциями (подшипника):

4. Добавляем активные силы (силы тяжести):

5. Записываем теорему об изменении кинетического момента системы относительно оси вращения блока:

R

Так как момент внешних сил равен нулю, то кинетический момент должен оставаться постоянным:

В начальный момент времени t = 0 было равновесие и Kz0 = 0.

После начала движения одного человека относительно каната вся система пришла в движение, но кинетический момент системы должен остаться равным нулю: Kz = 0.
Кинетический момент системы складывается из кинетических моментов обоих людей и блока:

Здесь v2 – скорость второго человека, равная скорости троса,

Пример: Определить период малых свободных колебаний однородного стержня массы M и длиной l, подвешенного одним концом к неподвижной оси вращения.

Или:

В случае малых колебаний sinφ  φ:

Период колебаний:

Момент инерции стержня:

Элементарная теория гироскопа:
Гироскоп – твердое тело, вращающееся вокруг оси материальной

симметрии, одна из точек которой неподвижна.
Свободный гироскоп – закреплен так, что его центр масс остается неподвижным, а ось вращения проходит через центр масс и может принимать любое положение в пространстве, т.е. ось вращения изменяет свое положение подобно оси собственного вращения тела при сферическом движении.

Основное допущение приближенной (элементарной) теории гироскопа – вектор момента количества
движения (кинетический момент) ротора считается направленным вдоль собственной оси вращения.
Таким образом, несмотря на то, что в общем случае ротор участвует в трех вращениях, принимается в расчет
только угловая скорость собственного вращения ω = dφ/dt. Основанием для этого является то, что
в современной технике ротор гироскопа вращается с угловой скоростью порядка 5000-8000 рад/c
(около 50000-80000 об/мин), в то время как две другие угловые скорости, связанные с прецессией и нутацией
собственной оси вращения в десятки тысяч раз меньше этой скорости.

Основное свойство свободного гироскопа – ось ротора сохраняет неизменное направление в пространстве по отношению к инерциальной (звездной) системе отсчета (демонстрируется маятником Фуко, сохраняющим неизменной по отношению к звездам плоскость качания, 1852 г.).
Это вытекает из закона сохранения кинетического момента относительно центра масс ротора при условии пренебрежения трением в подшипниках осей подвески ротора, внешней и внутренней рамы:

Действие силы на ось свободного гироскопа.
В случае действия силы, приложенной к оси ротора,
момент внешних сил относительно центра масс не равен нулю:

ω

ω

С

Производная кинетического момента по времени
равна скорости конца этого вектора (теорема Резаля):

Это означает, что ось ротора будет отклоняться не в сторону действия силы, а в сторону вектора момента
этой силы, т.е. будет поворачиваться не относительно оси x (внутренняя подвеска), а относительно оси y
(внешняя подвеска).

При прекращении действия силы ось ротора останется в неизменном положении, соответствующем
последнему моменту времени действия силы, т.к. с этого момента времени момент внешних сил вновь становится
равным нулю. В случае кратковременного действия силы (удара) ось гироскопа практически не меняет своего
положения.

Таким образом, быстрое вращение ротора сообщает гироскопу способность противодействовать случайным воздействиям,
стремящимся изменить положение оси вращения ротора, а при постоянном действии силы сохраняет положение плоскости,
перпендикулярной действующей силе, в которой лежит ось ротора. Эти свойства используются в работе инерциальных систем навигации.