Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КУРС ЛЕКЦИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ В ГЕОЛОГИИ Курамшин Ринат
Содержание
- 1. КУРС ЛЕКЦИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ В ГЕОЛОГИИ Курамшин Ринат
- 2. ОДНОМЕРНАЯ СТАТИСТИЧЕСКАЯМОДЕЛЬ И ЕЕ ПРИМЕНЕНИЕ В ГЕОЛОГИИ
- 3. СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫОдномерная
- 4. СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫВ
- 5. СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫВторая
- 6. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫВ основе большинства вычислений
- 7. СУЩНОСТЬ И ЗНАЧЕНИЕ СРЕДНИХ ПОКАЗАТЕЛЕЙСредняя величина представляет
- 8. В каждом конкретном случае для реализации исходного
- 9. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВАСредняя арифметическая простая
- 10. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВАСредняя арифметическая простая
- 11. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВАВ отдельных случаях
- 12. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА Свойства
- 13. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА3. Сумма квадратов
- 14. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВАНа использовании этого
- 15. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА5. Если все
- 16. ДРУГИЕ ВИДЫ СРЕДНИХСредняя гармоническая взвешенная. Рассмотрим вариант,
- 17. ДРУГИЕ ВИДЫ СРЕДНИХТаким образом, суммарная добыча по
- 18. Средняя гармоническая невзвешенная. Эта форма
- 19. Средняя квадратическая: невзвешенная взвешеннаяНаиболее широко этот вид
- 20. ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯДля вычисления по данным первичного
- 21. ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯМодой распределения (Мо) называется такая
- 22. ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯПРИМЕР: Распределение скважин всего НГДУ
- 23. Модальный интервал (т.е. содержащий моду) в случае
- 24. ПРИМЕР: Расчет моды для вариационного ряда распределения
- 25. Если в вариационном ряду 2m+1 случаев (нечетное
- 26. Если в ряду четное число 2m случаев,
- 27. ПРИМЕР 1: Определение медианы (нечетное число вариантов:
- 28. ПРИМЕР: Добыча нефти по скважинам за месяц.Необходимо
- 29. В интервальном ряду распределения сразу можно указать
- 30. Моду и медиану в интервальном
- 31. Медиана рассчитывается по кумуляте.Из точки на шкале
- 32. Таким образом, в качестве обобщенной характеристики значений
- 33. Соотношение моды, медианы и средней арифметической указывает
- 34. ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТАСредняя величина
- 35. ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТАК абсолютным
- 36. Вариационный размах (R) (амплитуда колебаний) показывает, насколько
- 37. Размах вариации существует, чтобы измерять расстояния между
- 38. Среднее линейное отклонение.Для анализа вариации необходим показатель,
- 39. Средняя применяется в качестве своего рода центра
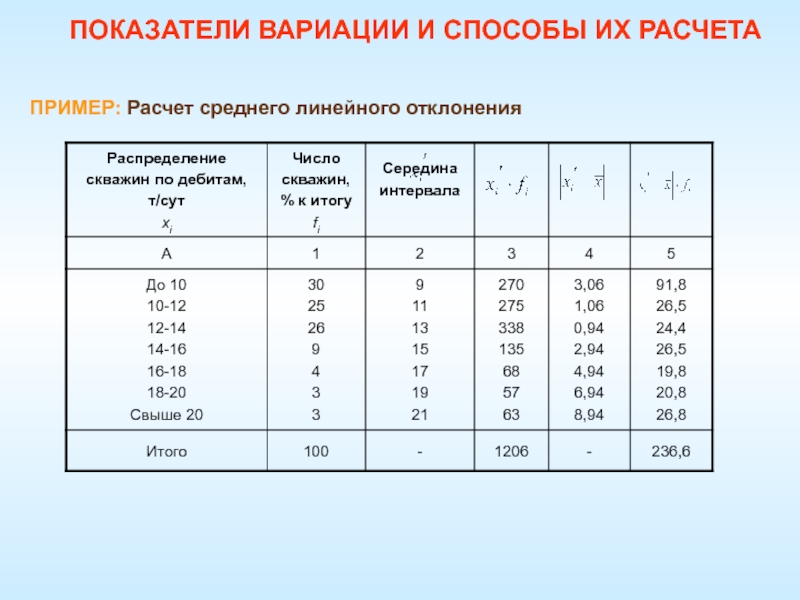
- 40. ПРИМЕР: Расчет среднего линейного отклонения ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
- 41. Алгоритм расчета среднего линейного отклонения:ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
- 42. Таково в среднем отклонение вариантов признака от
- 43. ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
- 44. Дисперсияпредставляет собой средний квадрат отклонений индивидуальных значений
- 45. Математические свойства дисперсии.1. Дисперсия постоянной величины равна
- 46. Математические свойства дисперсии.Средний квадрат отклонений при этом
- 47. На приведенных математических свойствах дисперсии основан метод
- 48. Среднее квадратическое отклонение (σ) равно корню квадратному
- 49. * Все степенные средние различаются между собой
- 50. ПРИМЕР: Вычисление σ2 и σ по несгруппированным
- 51. Для целей сравнения колеблемости различных признаков в
- 52. Коэффициент осцилляции (VR )Коэффициент вариации (Vσ )ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
- 53. Характеристика степени вариации ряда может быть определена
- 54. СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИРассмотренные
- 55. Квартили представляют собой значение признака, делящее ранжированную
- 56. Для расчета квартилей по интервальному вариационному ряду используют формулы:СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
- 57. Квинтили делят распределение на пять равных частей.Децили
- 58. Значения признака, делящие ряд распределения на сто
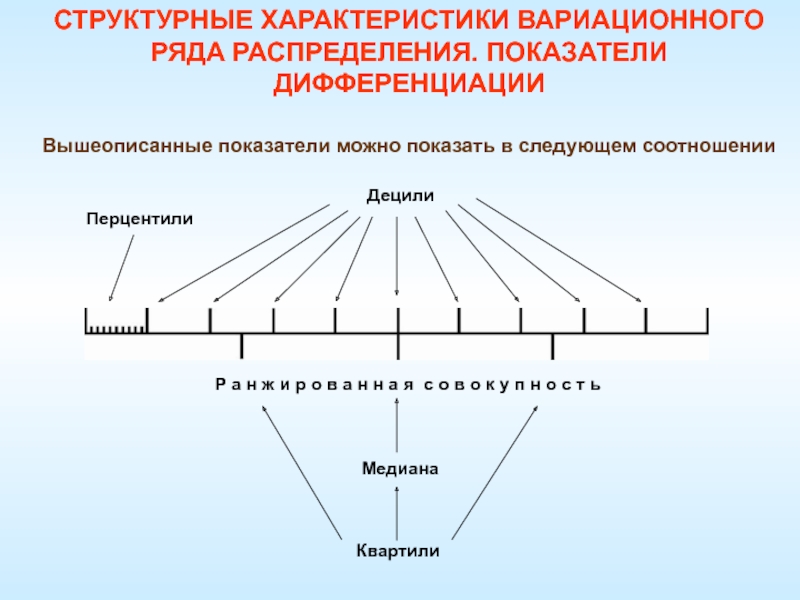
- 59. Вышеописанные показатели можно показать в следующем соотношенииСТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
- 60. Показатели дифференциации. В тех случаях, когда
- 61. 2. Если сопоставляются 9-я (d9)
- 62. МОМЕНТЫ РАСПРЕДЕЛЕНИЯДля подробного описания особенностей распределения используют
- 63. Порядок момента определяется величиной k. Эмпирический момент
- 64. 2. Условные и начальные относительно х0 моменты
- 65. Если отклонения (xi - x0) имеют общий
- 66. В статистической практике пользуются в основном моментами
- 67. Анализируя формулы моментов распределения, можно сделать следующие выводы:МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
- 68. МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
- 69. Методы обработки результатов экспериментальных исследований (выбор числа
- 70. ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙВторой способ
- 71. h – шаг интервалаR – размах вариации;Хmax
- 72. Если шаг интервала, рассчитанный по формуле, представляет
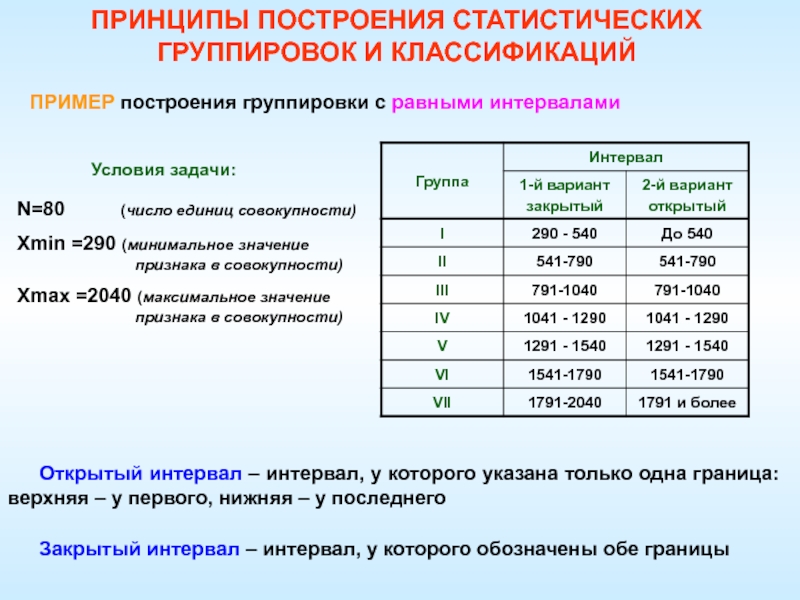
- 73. ПРИМЕР построения группировки с равными интерваламиУсловия задачи:N=80
- 74. Неравные интервалы применяются, когда значения признака варьируют
- 75. ПРИМЕР построения группировки с неравными интервалами изменяющихся
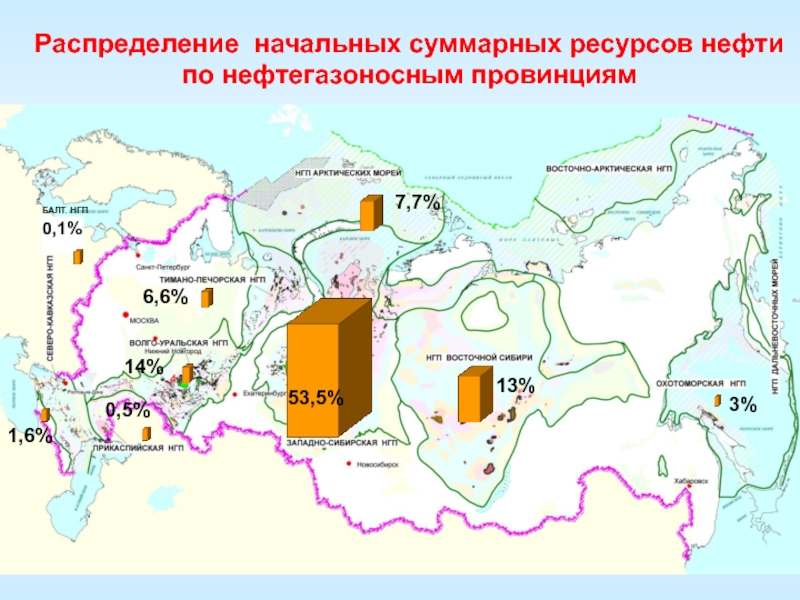
- 76. 53,5%13%3%7,7%6,6%14%0,5%1,6%БАЛТ. НГП 0,1%Распределение начальных суммарных ресурсов нефти по нефтегазоносным провинциям
- 77. в основе классификации лежит качественный признак;классификации стандартны:
- 78. РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИРяд распределения – ряд
- 79. Ряды распределения могут быть образованы:по качественному (атрибутивному)
- 80. В этом ряду группы составлены по признаку,
- 81. Интервальный вариационный ряд распределения В этом ряду
- 82. интервального вариационного ряда распределения с равными интерваламиПримеры
- 83. Плотность распределения используется в рядах распределения с
- 84. Для различных целей бываёт уместным осуществлять еще
- 85. Графическое изображение рядов распределенияДля изображения вариационных рядов
- 86. Графическое изображение рядов распределенияГистограмма (гр. histos –
- 87. Графическое изображение рядов распределенияДля графического изображения вариационных
- 88. Графическое изображение рядов распределенияЕсли в прямоугольной системе
- 89. Графическое изображение рядов распределенияРазновидностью кумулятивной кривой является
- 90. САМОСТОЯТЕЛЬНО к семинару 25.02.13г.:Привести примеры определения медианы и моды в интервальном ряду распределения.Решить задания №1,2,3,4.
- 91. ЗАДАНИЕ 1ИСХОДНЫЕ ДАННЫЕСреднее значение проницаемости ОПРЕДЕЛИТЬ и СДЕЛАТЬ ВЫВОД ПО ПОЛУЧЕННЫМ ДАННЫМ
- 92. ЗАДАНИЕ 2ИСХОДНЫЕ ДАННЫЕРассчитать моду.Определить медиану. Распределение начальной
- 93. ЗАДАНИЕ 3ИСХОДНЫЕ ДАННЫЕРаспределение остаточной нефтенасыщенности по образцам.
- 94. ЗАДАНИЕ 4ИСХОДНЫЕ ДАННЫЕРаспределение пористости по образцам. ОПРЕДЕЛИТЬ
- 95. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1КУРС ЛЕКЦИЙ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ В ГЕОЛОГИИ
Курамшин Ринат Мунирович
кандидат технических наук,
доцент
кафедры,
Слайд 3СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Одномерная статистическая модель применяется
для изучения одного свойства.
Пусть имеется система, состоящая из множества
однородных геологических объектов (параметров). Выборочным методом возьмем из множества n объектов и у каждого из них измерим характеристику свойства х.
Результаты измерений обозначим х1, х2, ..., хn и составим из них матрицу, в которой число строк равно n, а число столбцов k = 1.
Слайд 4СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В основе одномерной статистической
модели лежат три гипотезы:
измеренные значения х1, х2, …, хn носят
случайный характер; они не зависят друг от друга;
значения образуют однородную совокупность.
Измеренные значения принято называть реализациями случайной величины х.
Гипотеза о случайном характере свойств обусловлена тем, что природные геологические системы и объекты являются весьма сложными, на каждое измеренное значение влияет множество разнонаправленных факторов.
Кроме того, каждое измерение сопровождается случайной погрешностью.
Данная гипотеза позволяет применять для математической обработки значений х1, х2, …, хn аппарат (теоремы, формулы, уравнения, законы) теории вероятностей.
Слайд 5СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Вторая гипотеза о независимости
измеренных значений менее очевидна.
Предполагается, что на результат каждого отдельного
измерения не влияют результаты предыдущих или соседних измерений. Из этой гипотезы вытекает важное следствие, что для математической обработки не существенно пространственное размещение пунктов наблюдений, т.е. результаты измерений можно располагать в любом порядке, на выводы это не влияет.
Эта гипотеза не всегда соответствует действительности: соседние измерения нередко зависят друг от друга, что можно проверить с помощью специального математического аппарата.
Статистическая обработка результатов измерений имеет смысл лишь только для однородных совокупностей, что лежит в основе третьей гипотезы.
Если совокупность неоднородная, то ее необходимо разделить на однородные совокупности и каждую из них исследовать отдельно.
Слайд 6СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
В основе большинства вычислений лежит расчет статистических
характеристик случайной величины.
К наиболее распространенным статистическим характеристикам одномерной случайной
величины относятся: размах
медиана,
мода, среднее значение,
дисперсия,
среднеквадратичное отклонение,
коэффициент вариации,
асимметрия,
эксцесс и т.д.
Слайд 7СУЩНОСТЬ И ЗНАЧЕНИЕ СРЕДНИХ ПОКАЗАТЕЛЕЙ
Средняя величина представляет собой обобщенную количественную
характеристику признака в статистической совокупности в конкретных условиях места и
времени.Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Сущность средней величины заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных.
Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС)
Слайд 8В каждом конкретном случае для реализации исходного соотношения потребуется одна
из следующих форм средней величины:
средняя арифметическая;
средняя
гармоническая; средняя геометрическая;
средняя квадратическая, кубическая и т.д.
Перечисленные средние (кроме средней геометрической) объединяются в общей формуле средней степенной (при различной величине k):
Помимо степенных средних также используются средние структурные, среди которых наиболее распространены мода и медиана.
СУЩНОСТЬ И ЗНАЧЕНИЕ СРЕДНИХ ПОКАЗАТЕЛЕЙ
Слайд 9СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
Средняя арифметическая простая (невзвешенная).
Эта форма
средней используется в тех случаях, когда расчет осуществляется по несгруппированным
данным.ПРИМЕР: Добыча скважин за месяц
Слайд 10СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
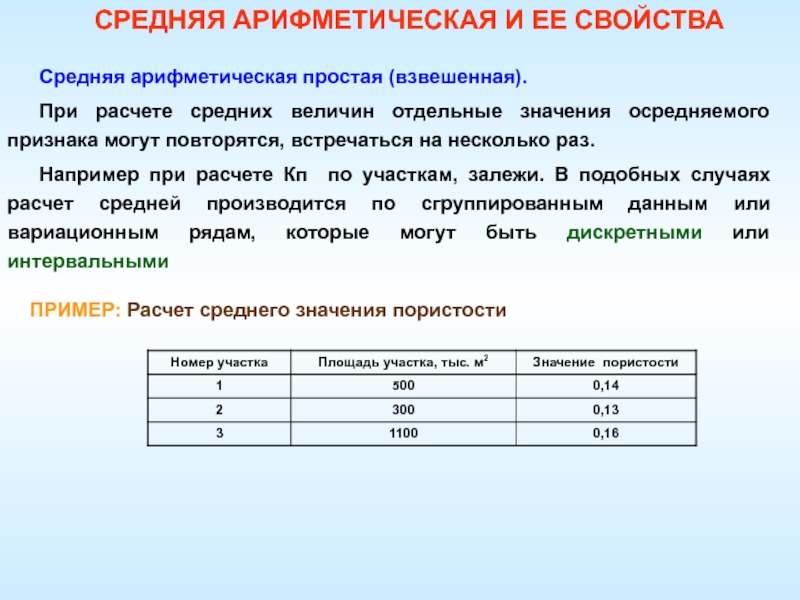
Средняя арифметическая простая (взвешенная).
При расчете
средних величин отдельные значения осредняемого признака могут повторятся, встречаться на
несколько раз.Например при расчете Кп по участкам, залежи. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными
ПРИМЕР: Расчет среднего значения пористости
Слайд 11СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
В отдельных случаях веса могут быть
представлены не абсолютными величинами, а относительными (в процентах или долях
единицы). Так, в приведенном примере площадь каждого участка соответственно составляет 26,3% (0,263), 15,8% (0,158) и 57,9% 90,579) от их общего числа.Следовательно:
Расчет среднего значения пористости выполнен по формуле средней арифметической взвешенной:
или
Использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.
Слайд 12СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
Свойства средней арифметической:
1. Произведение
средней на сумму частот равно сумме произведений отдельных вариантов на
соответствующие им частоты:2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
Слайд 13СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
3. Сумма квадратов отклонений индивидуальных значений
признака от средней арифметической меньше, чем сумма квадратов их отклонений
от любой другой произвольной величины С:Следовательно, сумма квадратов отклонений индивидуальных значений признака от произвольной величины С больше суммы квадратов их отклонений от своей средней на величину:
или
Свойства средней арифметической:
Слайд 14СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
На использовании этого свойства базируется расчет
центральных моментов, представляющих собой характеристики вариационного ряда при
4.
Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшиться или увеличиться на ту же величину: Свойства средней арифметической:
Слайд 15СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
5. Если все варианты значений признака
уменьшить или увеличить в А раз, то средняя арифметическая соответственно
уменьшиться или увеличиться в А раз:6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не измениться:
Свойства средней арифметической:
Слайд 16ДРУГИЕ ВИДЫ СРЕДНИХ
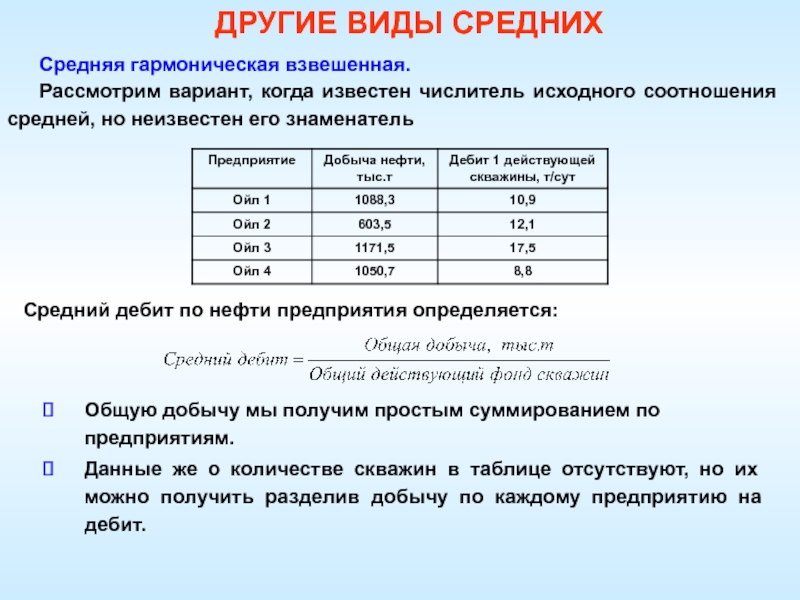
Средняя гармоническая взвешенная.
Рассмотрим вариант, когда известен числитель
исходного соотношения средней, но неизвестен его знаменатель
Средний дебит по нефти
предприятия определяется:Общую добычу мы получим простым суммированием по предприятиям.
Данные же о количестве скважин в таблице отсутствуют, но их можно получить разделив добычу по каждому предприятию на дебит.
Слайд 17ДРУГИЕ ВИДЫ СРЕДНИХ
Таким образом, суммарная добыча по предприятию составила 11,6
тыс.т на скважину.
Расчет был произведен по формуле средней гармонической взвешенной:
Слайд 18Средняя гармоническая невзвешенная.
Эта форма средней, используемая значительно
реже, имеет следующий вид:
Средняя геометрическая:
невзвешенная
взвешенная
Наиболее широкое применение этот
вид средней получил в анализе динамики для определения среднего темпа роста.ДРУГИЕ ВИДЫ СРЕДНИХ
Слайд 19Средняя квадратическая:
невзвешенная
взвешенная
Наиболее широко этот вид используется при расчете
показателей вариации.
В статистической практике также находят применение степенные средние 3-го
и более высоких порядков.ДРУГИЕ ВИДЫ СРЕДНИХ
Слайд 20ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Для вычисления по данным первичного ряда применяется формула
простой средней арифметической.
При вычислении по данным ранжированного вариационного ряда
применяется формула средней взвешенной.В отличие от средней арифметической, рассчитываемой на основе использования всех вариантов значений признака, мода и медиана характеризуют величину варианта, занимающего определенное положение в ранжированном вариационном ряду.
Слайд 21ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Модой распределения (Мо) называется такая величина изучаемого признака,
которая в данной совокупности встречается наиболее часто.
ПРИМЕР: Определение моды по
не сгруппированным даннымДебиты по 11 разведочным скважинам имеют следующие значения: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5. Чаще всего встречаются скважины с дебитом 5 т/сут, то это значение дебита и будет модальным.
Для упорядоченного дискретного ряда распределения мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариантов и соответствует варианту с наибольшей частотой.
Слайд 22ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
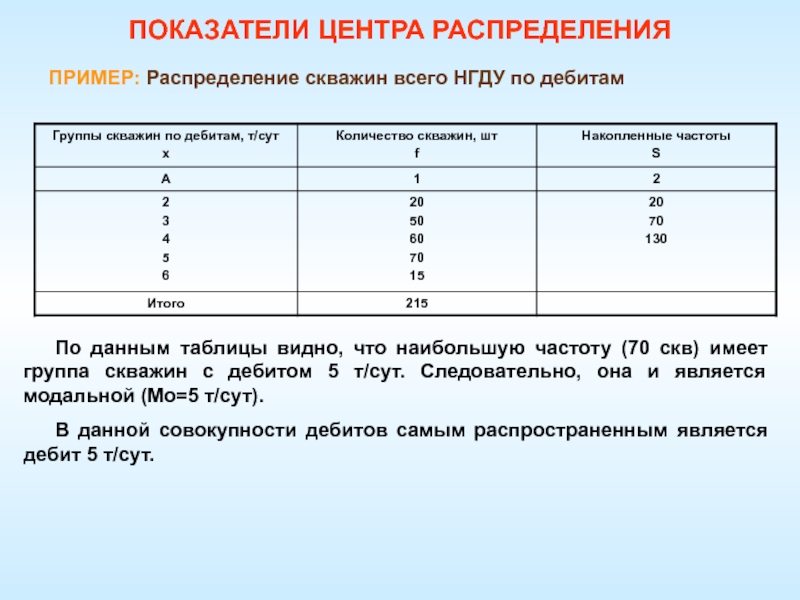
ПРИМЕР: Распределение скважин всего НГДУ по дебитам
По
данным таблицы видно, что наибольшую частоту (70 скв) имеет группа
скважин с дебитом 5 т/сут. Следовательно, она и является модальной (Мо=5 т/сут).В данной совокупности дебитов самым распространенным является дебит 5 т/сут.
Слайд 23Модальный интервал (т.е. содержащий моду) в случае интервального распределения с
равными интервалами определяется по наибольшей частоте; с неравными интервалами –
по наибольшей плотности, а определение моды требует проведение расчетов на основе формул:ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 24ПРИМЕР: Расчет моды для вариационного ряда распределения с равными интервалами
Интервал
с границами 4-5 в данном распределении будет модальным, так как
он имеет наибольшую частоту.Таким образом, в данной совокупности самым распространенным значением дебита является дебит со значением 4,2 т/сут.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 25Если в вариационном ряду 2m+1 случаев (нечетное число вариантов), то
значение признака у случая m+1 будет медианным.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
В
качестве характеристики вариационного ряда также применяется медиана (Ме).Медиана (Ме) – величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда.
Главное свойство медианы – сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Слайд 26Если в ряду четное число 2m случаев, то медиана равна
средней арифметической из двух данных значений.
Положение медианы в ряду распределения
(по сгруппированным данным) определяется ее номером:ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 27ПРИМЕР 1: Определение медианы (нечетное число вариантов: 2m+1)
Рассмотрим определение медианы
по данным вариационного ряда из 11 скважин, имеющих дебиты: 5,
4, 3, 4, 5, 5, 6, 2, 6, 3, 5 т/сут.Проведем ранжирование дебитов: 2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6 т/сут.
Центральным в этом ряду будет дебит 5 т/сут, следовательно, данный разряд и будет медианным
ПРИМЕР 2: Определение медианы (четное число вариантов: 2m)
Ранжированный ряд включает 12 скв.: 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6 т/сут.
В данном случае медиана определяется как средняя арифметическая из двух центральных значений:
Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функцию средней величины для неоднородной совокупности, не подчиняющейся нормальному закону распределения.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
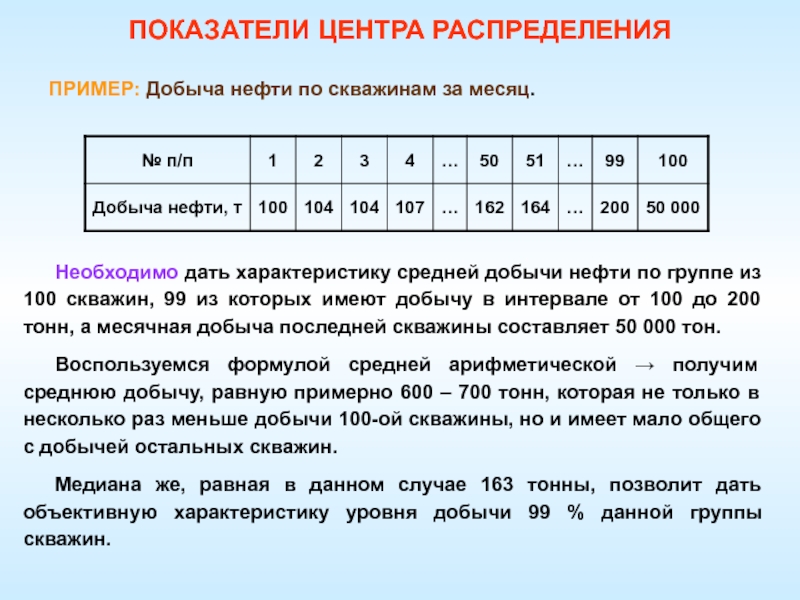
Слайд 28ПРИМЕР: Добыча нефти по скважинам за месяц.
Необходимо дать характеристику средней
добычи нефти по группе из 100 скважин, 99 из которых
имеют добычу в интервале от 100 до 200 тонн, а месячная добыча последней скважины составляет 50 000 тон.Воспользуемся формулой средней арифметической → получим среднюю добычу, равную примерно 600 – 700 тонн, которая не только в несколько раз меньше добычи 100-ой скважины, но и имеет мало общего с добычей остальных скважин.
Медиана же, равная в данном случае 163 тонны, позволит дать объективную характеристику уровня добычи 99 % данной группы скважин.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 29В интервальном ряду распределения сразу можно указать только интервал, в
котором будет находиться медиана.
Для определения ее величины используется специальная формула:
где
x0 – нижняя граница медианного интервала;i – величина медианного интервала;
SMe-1 – накопленная частота интервала, предшествующего медианному;
fМе – частота медианного интервала
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
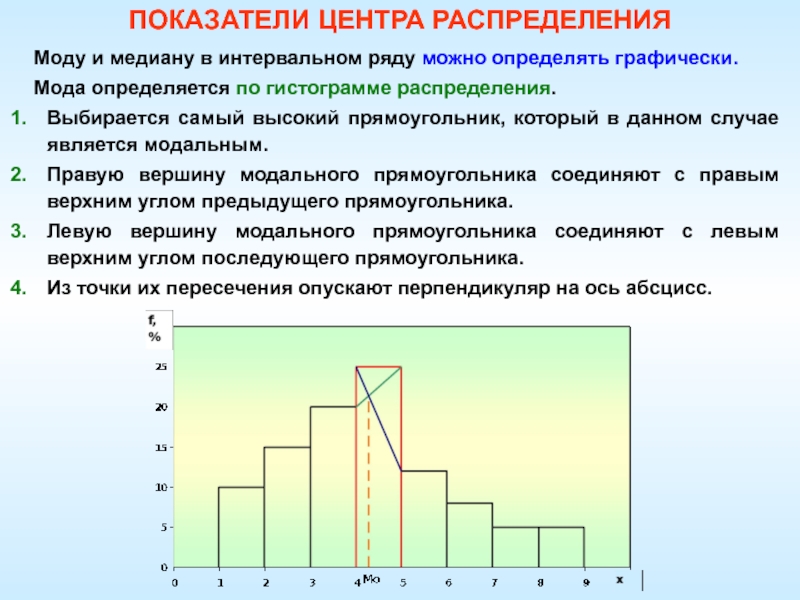
Слайд 30 Моду и медиану в интервальном ряду можно определять
графически.
Мода определяется по гистограмме распределения.
Выбирается самый высокий прямоугольник,
который в данном случае является модальным. Правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника.
Левую вершину модального прямоугольника соединяют с левым верхним углом последующего прямоугольника.
Из точки их пересечения опускают перпендикуляр на ось абсцисс.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
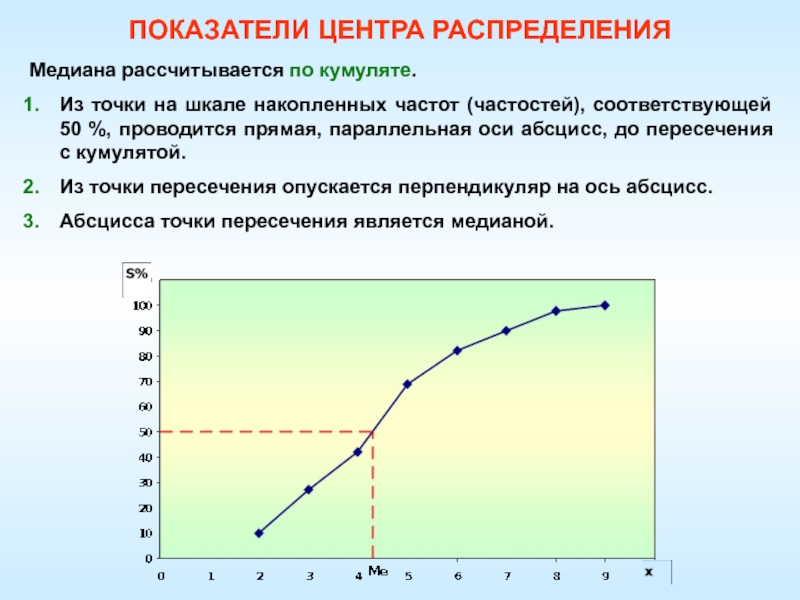
Слайд 31Медиана рассчитывается по кумуляте.
Из точки на шкале накопленных частот (частостей),
соответствующей 50 %, проводится прямая, параллельная оси абсцисс, до пересечения
с кумулятой.Из точки пересечения опускается перпендикуляр на ось абсцисс.
Абсцисса точки пересечения является медианой.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 32Таким образом, в качестве обобщенной характеристики значений определенного признака у
единиц ранжированной совокупности могут быть использованы:
средняя арифметическая
мода
медиана
Каждая их них имеет
свои особенности.Основной характеристикой центра распределения является средняя арифметическая, для которой характерно то, что все отклонения от нее (положительные или отрицательные) в сумме равны нулю.
Для медианы характерно то, что сумма отклонений от нее по модулю является минимальной.
Мода представляет собой значение признака, которое наиболее часто встречается.
В зависимости от цели исследования распределения должна выбираться одна из упомянутых характеристик, либо же для сравнения вычисляются все три.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 33Соотношение моды, медианы и средней арифметической указывает на характер распределения
признака в совокупности, позволяет оценить его асимметрию.
В симметричных распределениях
все три характеристики совпадают.Чем больше расхождение между модой и средней арифметической, тем более асимметричен ряд.
Для умеренно асимметричных рядов разность между модой и средней примерно в три раза превышает разность между медианой и средней.
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
Слайд 34ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Средняя величина дает обобщающую характеристику
всей совокупности изучаемого явления.
Однако, исчислив среднюю арифметическую по данным
вариационного ряда, мы еще ничего не знаем о том, как отдельные значения изучаемого признака группируются вокруг средней. Нельзя ограничиться вычислением одной средней величины, надо изучать не только среднюю, но и отклонение от нее.
Для вариационного ряда важно изучать степень сплоченности всех отдельных значений параметра (признака) вокруг его среднего значения, степень разбросанности этих значений, степень их колеблемости.
Для это в теории статистики используются показатели вариации.
Показатели вариации делятся на две группы:
абсолютные
относительные.
Слайд 35ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
К абсолютным показателям относятся: размах
вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
К
относительным показателям относятся: коэффициенты осцилляции, вариации, относительное линейное отклонение и др.Относительные показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане).
Слайд 36Вариационный размах (R) (амплитуда колебаний) показывает, насколько велико различие между
единицами совокупности, имеющими самое маленькое и самое большое значение признака.
Размах
рассчитывают как разность между наибольшим (хmax) и наименьшим (xmin) значениями варьирующего признака:НАПРИМЕР: пористость, проницаемость, толщина.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 37Размах вариации существует, чтобы измерять расстояния между крайними точками.
Недостатки
размаха вариации:
очень низкое и очень высокое значение параметра (признака) по
сравнению с основной массой его значений в совокупности могут быть обусловлены какими-либо сугубо случайными обстоятельствами, т.е. эти значения являются аномальными в совокупности.В этих случаях размах вариации даст искаженную амплитуду колебания параметра (признака).
Поэтому прежде чем определить величину размаха вариации, следует очистить совокупность от аномальных наблюдений.
Размах вариации – важный показатель изменения параметра (признака), но он не исчерпывает характеристику вариации.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 38Среднее линейное отклонение.
Для анализа вариации необходим показатель, который бы отражал
все колебания варьирующего признака и давал обобщенную его характеристику.
Для
многих варьирующих признаков возможно допущение, что при прочих равных условиях все единицы совокупности в соответствии с основными законами своего распределения имеют одинаковую и при этом вполне определенную величину в данных условиях места и времени.Вполне логично в качестве такой величины условно принять среднюю величину из всех значений признака, поскольку в ней более или менее погашаются случайные отклонения от закономерного развития явления, и средняя тем самым отражает типичный размер признака у данной однородной совокупности единиц.
Но условия существования и развития отдельных единиц совокупности в определенной степени различны, что сказывается на различии значений признака.
Средняя величина отражает эти средние условия.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 39Средняя применяется в качестве своего рода центра тяжести, вокруг которого
происходит колебание, рассеяние значений параметра (признака).
При обобщении этих колебаний необходимо
прибегать к методу средних величин – искать среднюю величину этих отклонений. простая:
взвешенная:
Поскольку сума отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 42Таково в среднем отклонение вариантов признака от их средней величины.
Это отклонение по сравнению со средней величиной признака небольшое.
Оно отличается
от средней на 9,694 т/сут.Это свидетельствует о том, что данная совокупность в отношении нашего признака однородна, а средняя - типична
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 44Дисперсия
представляет собой средний квадрат отклонений индивидуальных значений признака от их
средней величины и в зависимости от исходных данных вычисляется по
формулам:простой дисперсии:
взвешенной дисперсии:
Расчет дисперсии может быть упрощен.
В случае равных интервалов в вариационном ряду распределения используется способ отсчета от условного нуля (способ моментов).
Для его понимания необходимо знать математические свойства дисперсии.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 45Математические свойства дисперсии.
1. Дисперсия постоянной величины равна нулю.
2. Уменьшение всех
значений признака на одну и ту же величину А не
меняет величину дисперсии.3. Уменьшение всех значений признака в k раз уменьшает дисперсию в k2 раз, а среднее квадратическое отклонение – в k раз.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 46Математические свойства дисперсии.
Средний квадрат отклонений при этом будет больше на
вполне определенную величину – на квадрат разности средней и этой
условно взятой величины:или
Дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности
В случае когда А приравнивается к нулю, отклонения не вычисляются, формула принимает вид:
или
Средний квадрат отклонений равен среднему квадрату значений признака минус квадрат среднего значения признака.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 47На приведенных математических свойствах дисперсии основан метод расчета дисперсии по
способу моментов, или способу отсчета от условного нуля, который применяется
при исчислении средней величины.Расчет производится по формуле:
где k – ширина интервала;
A – условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
Дисперсия есть средняя величина квадратов отклонений, а варианты признака выражены в первой степени.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 48Среднее квадратическое отклонение (σ) равно корню квадратному из дисперсии.
простое:
взвешенное:
Среднее
квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько
в среднем отклоняются конкретные варианты признака от среднего значения.Они выражаются в тех же единицах измерения, что и признак (в метрах, тоннах и т.д.).
Среднее квадратическое отклонение часто используется в качестве единицы измерения отклонений от средней арифметической.
В зарубежной литературе этот показатель называется нормированным или стандартизированным отклонением.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 49* Все степенные средние различаются между собой значениями показателя степени.
При этом, чем выше показатель степени, тем больше количественное значение
среднего показателя.Среднее квадратическое отклонение играет важную роль в анализе вариационных рядов распределения.
В условиях нормального распределения существует следующая взаимосвязь между величиной среднего квадратического отклонения и количеством наблюдений:
В действительности на практике почти не встречаются отклонения, которые превышают ±3σ. Отклонение 3σ считается максимально возможным. Это положение называется правилом трех сигм.
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
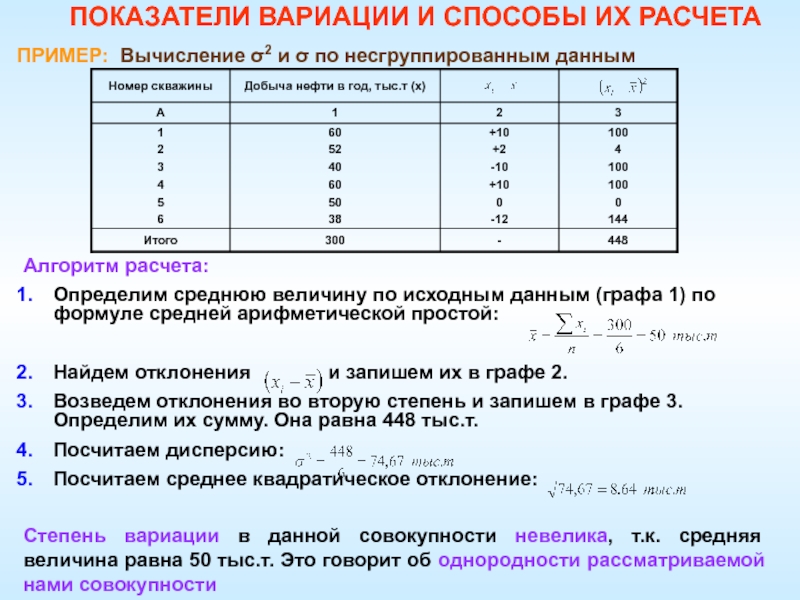
Слайд 50ПРИМЕР: Вычисление σ2 и σ по несгруппированным данным
Степень вариации в
данной совокупности невелика, т.к. средняя величина равна 50 тыс.т. Это
говорит об однородности рассматриваемой нами совокупностиПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 51Для целей сравнения колеблемости различных признаков в одной и той
же совокупности или же при сравнении колеблемости одного и того
же признака в нескольких совокупностях представляют интерес показатели вариации, приведенные в относительных величинах.Базой для сравнения должна служить средняя арифметическая.
Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане.
Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности.
Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Различают следующие относительные показатели вариации (V):
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 52Коэффициент осцилляции (VR )
Коэффициент вариации (Vσ )
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ
ИХ РАСЧЕТА
Слайд 53Характеристика степени вариации ряда может быть определена также по формуле
квартильного отклонения (Q), предложенной английским биологом и антропологом Ф. Гальтоном:
где
Q3 и Q1 – соответственно 1-ая и 3-я квартили распределенияЭта формула дает абсолютный квартильный показатель вариации.
В симметричных или умеренно симметричных распределениях Q=2/3σ/
Так как на квартильное отклонение не влияют отклонения всех значений признака, то его использование следует ограничить случаями, когда определение среднего квадратического отклонения затруднено или невозможно.
В частности, этот показатель может быть рекомендован для рядов распределения с открытыми интервалами.
В целях сравнения вариации в различных рядах вычисляют относительный квартильный показатель вариации по формуле:
где Ме – медиана ряда распределения
ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА
Слайд 54СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Рассмотренные обобщающие показатели центра
распределения и степени вариации не дают понятия о форме распределения,
т.е. не вскрывают характера последовательности изменения частот.Для выражения особенностей формы распределения применяются показатели дифференциации, основанные на структурных (ранговых) показателях распределения.
Структурные показатели.
В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место (каждое четвертое, пятое, десятое, двадцать пятое и т.д.) в ранжированном вариационном ряду.
Такие показатели носят общее название квантилей или градиентов.
Некоторые квантили имеют особые наименования: квартили, квинтили, децили и перцентили.
Слайд 55Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре
равновеликие части.
Различают:
квартиль нижний (Q1), отделяющий ¼ часть совокупности с
наименьшими значениями признака, квартиль верхний (Q3), отсекающий ¼ часть с наибольшими значениями признака.
Вторая квартиль Q2 является медианой.
Вычисление квартилей аналогично вычислению медианы.
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
25% единиц совокупности будут меньше по величине Q1;
25% единиц будут заключены между Q1 и Q2;
25 % единиц будут заключены между Q2 и Q3;
25% единиц превзойдут Q3.
Это означает, что:
Слайд 56Для расчета квартилей по интервальному вариационному ряду используют формулы:
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ
ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Слайд 57Квинтили делят распределение на пять равных частей.
Децили (di) -
это значения вариант, которые делят ранжированный ряд на десять равных
частей:1-й дециль (d1) делит совокупность в соотношении 1/10 к 9/10,
2-й дециль (d2) – в соотношении 2/10 к 8/10 и т.д.
и т.д.
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Вычисляются децили по той же схеме, что и медиана, и квартили:
Слайд 58Значения признака, делящие ряд распределения на сто частей, называются перцентилями.
Слово «перцентиль» относится непосредственно к элементу распределения или к значению,
промежуточному между двумя элементами. Для того чтобы указать местоположение конкретного наблюдения, в распределении указывается так называемый перцентильный ранг, который равен сумме процентов, приходящихся на наблюдения, которые в распределении стоят ниже его, и половине процентов, которые приходятся на него непосредственно.
Метод нахождения перцентилей можно представить с помощью следующей формулы:
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Слайд 59Вышеописанные показатели можно показать в следующем соотношении
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА
РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Слайд 60Показатели дифференциации.
В тех случаях, когда при изучении
вариационного ряда возникает необходимость дать относительную характеристику степени вариации ряда
и имеются уже предварительно вычисленные квартили и децили, то можно вычислить коэффициент дифференциации (К).В зависимости от заданных ранговых показателей коэффициенты дифференциации рассчитываются по-разному
1. Если заданы 3-я (Q3) и 1-я (Q1) квартили, то вместо коэффициента вариации (V), можно вычислить коэффициент дифференциации по формуле:
В большинстве случаев коэффициент вариации (V) составляет примерно 1,5 коэффициента дифференциации (Kv), т.е.
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Слайд 61 2. Если сопоставляются 9-я (d9) и 1-я (d1)
децили, то децильный коэффициент дифференциации (Kd) вычисляется по формуле:
3. Более точно уровень дифференциации можно измерить, сопоставив средние уровни, полученные из 10 % наибольших и наименьших значений признака в совокупности.Такой показатель называется коэффициентом фондовой дифференциации (Кф):
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ
Слайд 62МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Для подробного описания особенностей распределения используют дополнительные характеристики, в
частности определяются моменты распределения.
Способ моментов был разработан русским математиком П.Л.Чебышевым
и успешно применен А.А. Марковым для рассмотрения возможностей использования закона нормального распределения при изучении сумм большого, но конечного числа независимых случайных величин. Моментом k-го порядка называется средняя из k-х степеней отклонений вариантов х от некоторой постоянной величины А:
При исчислении средней в качестве весов могут быть использованы частоты, частости или вероятности. При использовании в качестве весов частот или частостей моменты называются эмпирическими, а при использовании вероятностей – теоретическими.
Слайд 63Порядок момента определяется величиной k.
Эмпирический момент k–го порядка определяется
как соотношение суммы произведений k–х степеней отклонений вариантов от постоянной
величины А на частоты к сумме частот:В зависимости от выбора постоянной величины А различают три вида моментов:
1. Начальные моменты (Мk) получаются, если постоянная величина А равна нулю (А=0):
МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Слайд 642. Условные и начальные относительно х0 моменты (mk) получаются при
А равном не нулю, а некоторой производной величине х0 (начало
отсчета):С помощью условных моментов упрощается расчет основных характеристик ряда распределения. При подстановке различных значений k получаем начальные моменты относительно х0. Так, например, если k=1, то:
МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Слайд 65Если отклонения (xi - x0) имеют общий множитель C, то
на него можно разделить отклонения, а по окончании вычислить полученный
момент, умножив на этот множитель в соответствующей степени, т.е.:МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Слайд 66В статистической практике пользуются в основном моментами 1-го, 2-го, 3-го,
4-го порядков, которые представлены в таблице
МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Слайд 67Анализируя формулы моментов распределения, можно сделать следующие выводы:
МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
Слайд 69Методы обработки результатов экспериментальных исследований (выбор числа групп)
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ
ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Согласно формуле Стерджесса выбор числа групп зависит от
объема совокупности.Недостаток формулы состоит в том, что ее применение дает хорошие результаты, если совокупность состоит из большого числа единиц и распределение единиц по признаку, положенному в основание группировки, близко к нормальному.
Существует несколько способов определения оптимального числа групп
Первый способ (метод) - Формула Стерджесса
n - число групп
N - число единиц совокупности
Слайд 70ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Второй способ (метод) - Применение
показателя среднего квадратического отклонения (σ)
Весь диапазон изменения показателя предполагается равным.
величина интервала равна 0,5σ – совокупность разбивается на 12 групп,
величина интервала равна 2/3σ – совокупность разбивается на 9 групп,
величина интервала равна σ – совокупность разбивается на 6 групп
Однако при определении числа групп данными методами существует большая вероятность получения «пустых» или малочисленных групп.
«Пустыми» считаются группы, в которые не попала ни одна единица совокупности. Поэтому данными формулами нельзя пользоваться механически. Их показания требуют корректировки.
Слайд 71h – шаг интервала
R – размах вариации;
Хmax – максимальное значение
признака в совокупности
Хmin –минимальное значения признака в совокупности;
n – число
группИнтервал группировки - это интервал значений варьирующего признака, лежащих в пределах определенной группы.
Каждый интервал имеет свою ширину, верхнюю и нижнюю границы или хотя бы одну из них.
Нижняя граница интервала – наименьшее значение признака в интервале, а верхняя граница – наибольшее значение признака в нем.
Ширина интервала (ее еще часто называют интервальной разностью) –разность между верхней и нижней границами интервала.
Интервалы группировки бывают равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные.
Если вариация признака проявляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то строят группировку с равными интервалами.
Величина равного интервала определяется по следующей формуле:
R = Хmax – Хmin
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Слайд 72Если шаг интервала, рассчитанный по формуле, представляет собой величину, имеющую
один знак до запятой (например: 0,86; 1,372; 5,8), то в
этом случае полученные значения целесообразно округлить до десятых долей.Когда шаг интервала имеет две значащие цифры до запятой и несколько знаков после запятой, то это значение надо округлить до целого числа.
Когда шаг интервала представляет собой трехзначное, четырехзначное и так далее число, эту величину необходимо округлить до ближайшего числа, кратного 100 или 50.
Правила определения, шага интервала
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Слайд 73ПРИМЕР построения группировки с равными интервалами
Условия задачи:
N=80
(число единиц совокупности)
Хmin =290 (минимальное значение признака в совокупности)
Хmax
=2040 (максимальное значение признака в совокупности)Открытый интервал – интервал, у которого указана только одна граница: верхняя – у первого, нижняя – у последнего
Закрытый интервал – интервал, у которого обозначены обе границы
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Слайд 74Неравные интервалы применяются, когда значения признака варьируют неравномерно и в
значительных размерах, что характерно для толщин пластов, дебитов скважин и
т.д.Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии, специализированные и произвольные.
Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом:
в геометрической прогрессии:
a-константа – число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным при прогрессивно убывающих интервалах;
q-константа –положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих - меньше 1.
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Слайд 75ПРИМЕР построения группировки с неравными интервалами изменяющихся в арифметической прогрессии
Специализированные
интервалы группировок – интервалы, применяющиеся для выделения из совокупности одних
и тех же типов по одному и тому же признаку явлений (параметров), находящихся в различных условиях.Произвольные интервалы группировок – применяются при изучении на макроуровне.
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Слайд 7653,5%
13%
3%
7,7%
6,6%
14%
0,5%
1,6%
БАЛТ. НГП 0,1%
Распределение начальных суммарных ресурсов нефти по нефтегазоносным провинциям
Слайд 77в основе классификации лежит качественный признак;
классификации стандартны: они устанавливаются органами
государственной и международной статистики. Если в каждом конкретном исследовании строится
своя группировка, то классификация едина для любого исследования независимо от того, проводят его органы государственной статистики или другие учреждения и ведомства (например: форма 6ГР министерства МПР РФ, Классификация запасов и т.п.);классификации устойчивы. Они остаются неизменными в течение длительного времени. Однако если появляются новые группы единиц, их классы, разряды, то в классификации вносятся соответствующие изменения и дополнения.
От группировок следует отличать классификацию.
Классификация – систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.
Отличительные черты классификации:
ПРИНЦИПЫ ПОСТРОЕНИЯ СТАТИСТИЧЕСКИХ ГРУППИРОВОК И КЛАССИФИКАЦИЙ
Цель классификации - однозначно идентифицировать единицы совокупности, обеспечить эффективный поиск информации и ее систематизацию, достичь сопоставимости с международными стандартами.
Слайд 78РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Ряд распределения – ряд цифровых показателей, представляющих
распределение единиц совокупности по одному существенному признаку, разновидности которого расположены
в определенной последовательности.По своей конструкции ряд распределения состоит из двух элементов:
вариантов (групп по выделенному признаку)
частот (численности групп).
Частоты, выраженные в виде относительных величин (доли единиц, процентов), называются частостями.
Сумма всех частот называется объемом распределения, или его численностью.
Сумма частостей равна 1, если они выражены в долях единицы, и 100%, если они выражены в процентах. Он оформляется в виде статистической таблицы.
Слайд 79Ряды распределения могут быть образованы:
по качественному (атрибутивному) признаку;
по количественному
(прерывному или непрерывному) признаку.
В первом случае они называются атрибутивными, во
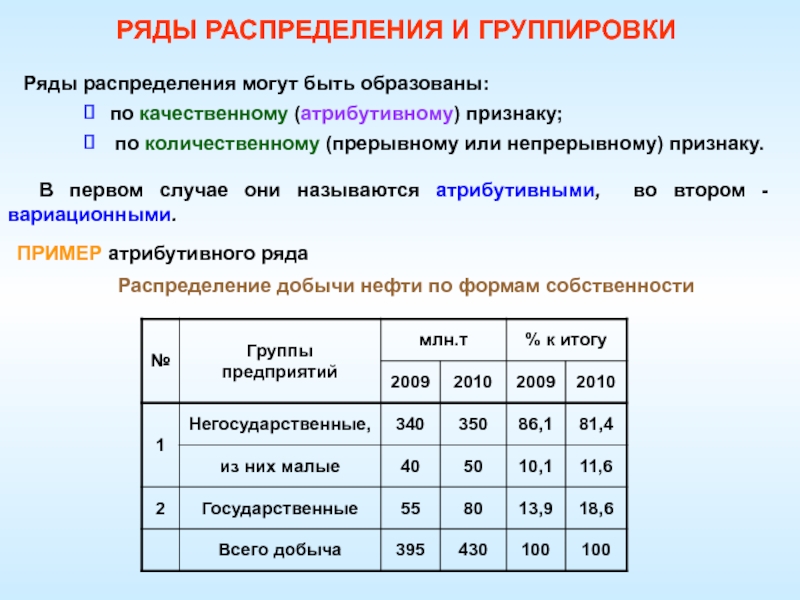
втором - вариационными.ПРИМЕР атрибутивного ряда
Распределение добычи нефти по формам собственности
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
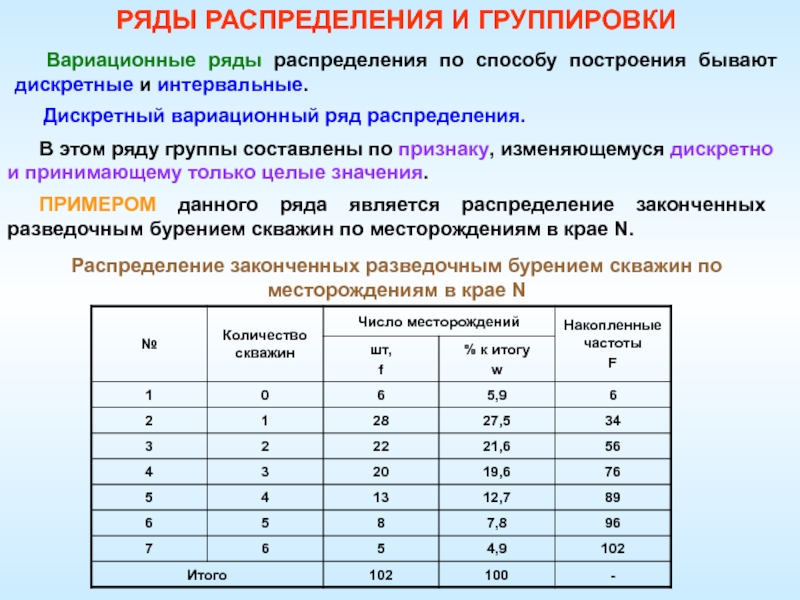
Слайд 80В этом ряду группы составлены по признаку, изменяющемуся дискретно и
принимающему только целые значения.
ПРИМЕРОМ данного ряда является распределение законченных
разведочным бурением скважин по месторождениям в крае N.Вариационные ряды распределения по способу построения бывают дискретные и интервальные.
Дискретный вариационный ряд распределения.
Распределение законченных разведочным бурением скважин по месторождениям в крае N
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 81Интервальный вариационный ряд распределения
В этом ряду в группировочный признак,
составляющий основание группировки, может принимать в определенном интервале любые значения.
Данный ряд распределения целесообразно строить прежде всего при непрерывной вариации признака, а также если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико.
Интервальный вариационный ряд распределения с равными интервалами
В этом случае частоты позволяют судить о степени заполнения интервала единицами совокупности.
Интервальный вариационный ряд распределения с неравными интервалами
В этом случае частоты в отдельных интервалах непосредственно несопоставимы, так как зависят от ширины интервала.
Для того чтобы частоты можно было бы сравнивать, исчисляют плотность распределения. Можно рассчитать как абсолютную, так и относительную плотность распределения
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
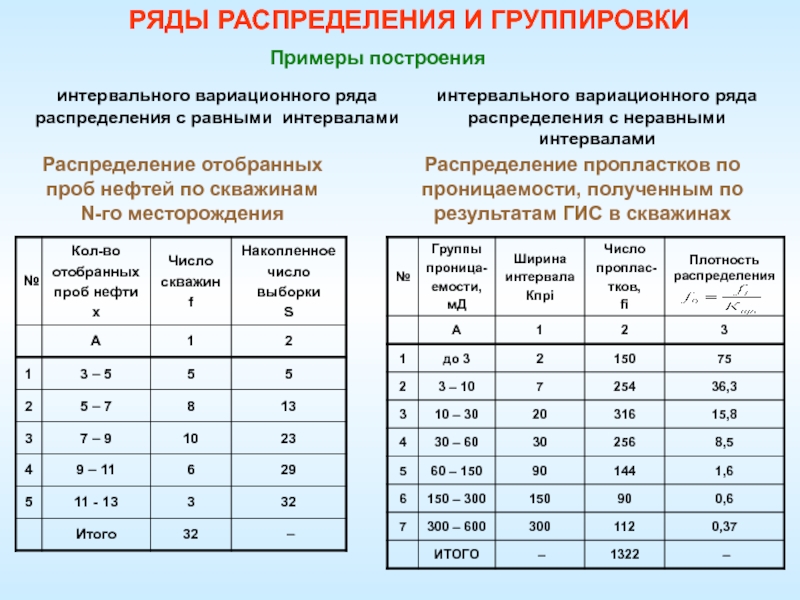
Слайд 82интервального вариационного ряда
распределения с равными интервалами
Примеры построения
интервального вариационного ряда
распределения с неравными интервалами
Распределение отобранных проб нефтей по скважинам
N-го
месторожденияРаспределение пропластков по проницаемости, полученным по результатам ГИС в скважинах
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 83Плотность распределения используется в рядах распределения с неравными интервалами:
для расчета моды (*САМОСТОЯТЕЛЬНО рассмотреть к семинару расчёт моды)
для графического изображения Абсолютная плотность распределения
это частота, приходящаяся на единицу длины интервала
Относительная плотность распределения
это частость, приходящаяся на единицу длины интервала
Плотность распределения
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 84Для различных целей бываёт уместным осуществлять еще одно преобразование ряда
распределения, заключающееся в построении ряда накопленных частот (кумулятивного ряда).
Кумулятивный
рядодин показывает число случаев, менее определенного значения варьирующего признака,
а другой - число случаев, превышающее определенное значение варьирующего признака.
Этот ряд показывает число случаев ниже или выше определенного уровня.
Отсюда и возникают два варианта в построении ряда накопленных частот:
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
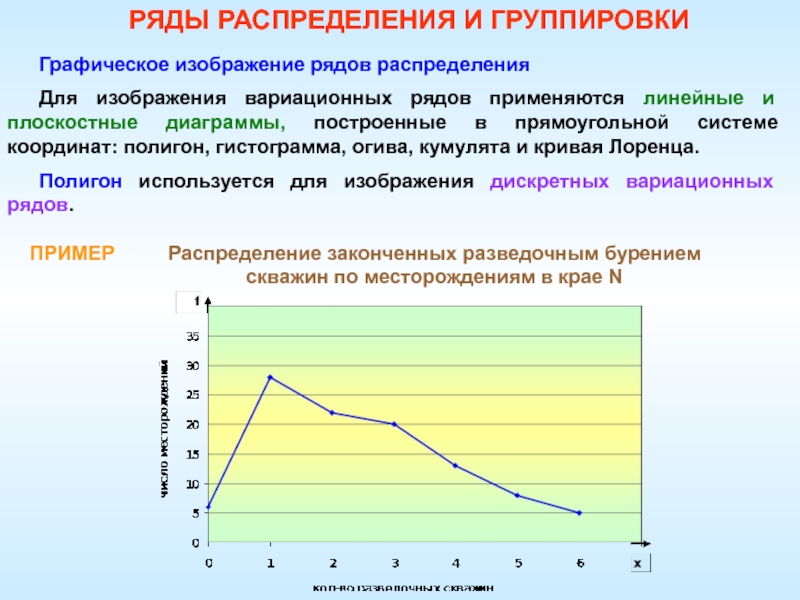
Слайд 85Графическое изображение рядов распределения
Для изображения вариационных рядов применяются линейные и
плоскостные диаграммы, построенные в прямоугольной системе координат: полигон, гистограмма, огива,
кумулята и кривая Лоренца.Полигон используется для изображения дискретных вариационных рядов.
ПРИМЕР
Распределение законченных разведочным бурением скважин по месторождениям в крае N
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
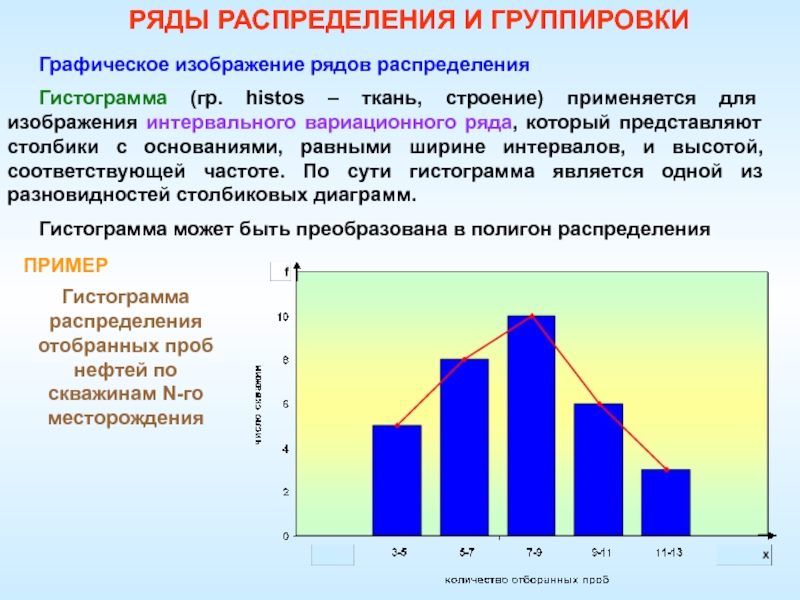
Слайд 86Графическое изображение рядов распределения
Гистограмма (гр. histos – ткань, строение) применяется
для изображения интервального вариационного ряда, который представляют столбики с основаниями,
равными ширине интервалов, и высотой, соответствующей частоте. По сути гистограмма является одной из разновидностей столбиковых диаграмм.Гистограмма может быть преобразована в полигон распределения
ПРИМЕР
Гистограмма распределения отобранных проб нефтей по скважинам N-го месторождения
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 87Графическое изображение рядов распределения
Для графического изображения вариационных рядов может также
использоваться кумулятивная кривая.
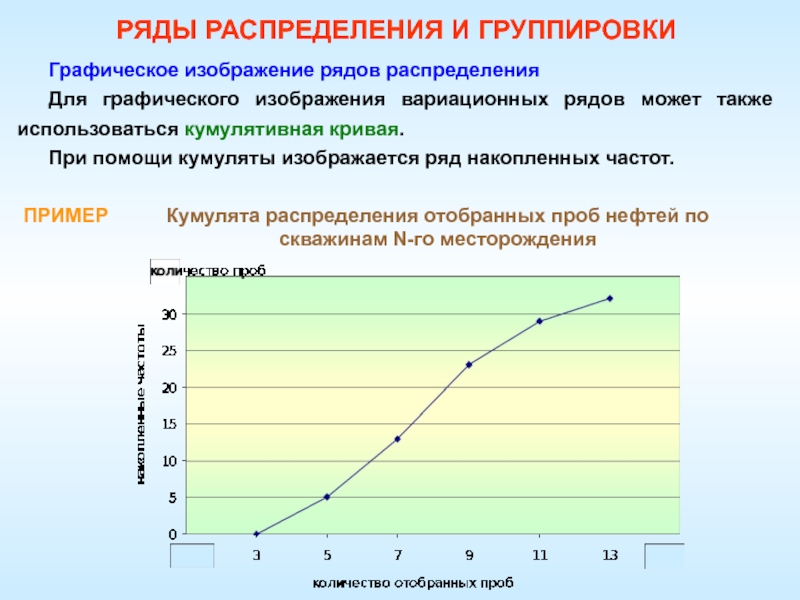
При помощи кумуляты изображается ряд накопленных частот.
ПРИМЕР
Кумулята
распределения отобранных проб нефтей по скважинам N-го месторожденияРЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 88Графическое изображение рядов распределения
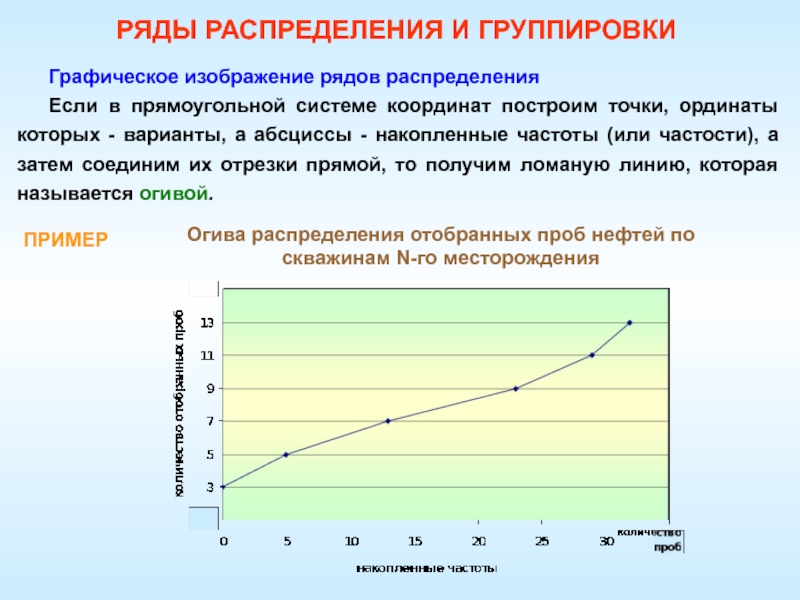
Если в прямоугольной системе координат построим точки,
ординаты которых - варианты, а абсциссы - накопленные частоты (или
частости), а затем соединим их отрезки прямой, то получим ломаную линию, которая называется огивой.ПРИМЕР
Огива распределения отобранных проб нефтей по скважинам N-го месторождения
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 89Графическое изображение рядов распределения
Разновидностью кумулятивной кривой является график-кривая Лоренца. График
используется для характеристики процессов концентрации, дифференциации, специализации и т.д.
В геологии
практически не используется.РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРУППИРОВКИ
Слайд 90САМОСТОЯТЕЛЬНО
к семинару 25.02.13г.:
Привести примеры определения медианы и моды в
интервальном ряду распределения.
Решить задания №1,2,3,4.
Слайд 91ЗАДАНИЕ 1
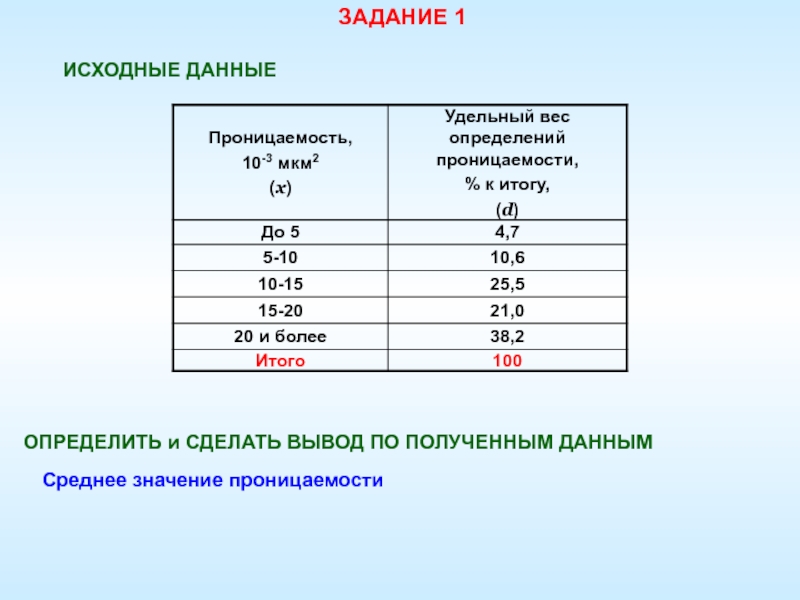
ИСХОДНЫЕ ДАННЫЕ
Среднее значение проницаемости
ОПРЕДЕЛИТЬ и СДЕЛАТЬ ВЫВОД ПО
ПОЛУЧЕННЫМ ДАННЫМ
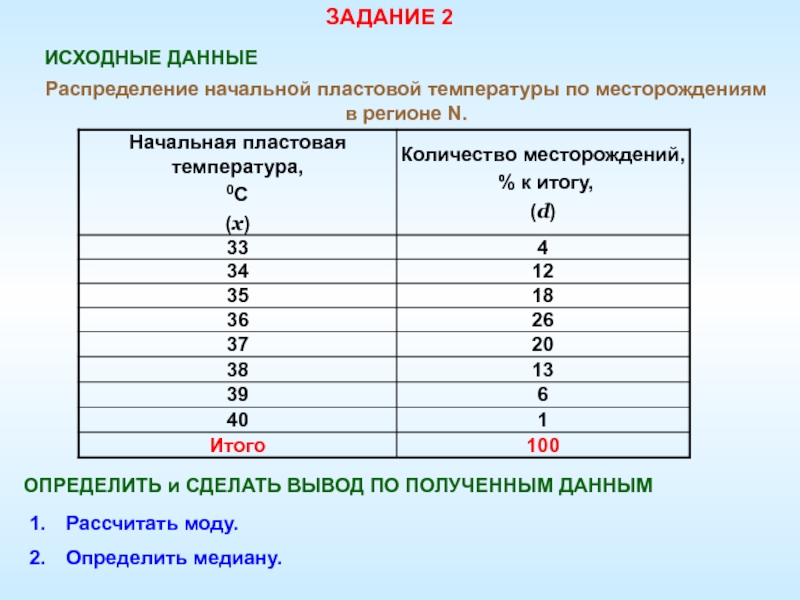
Слайд 92ЗАДАНИЕ 2
ИСХОДНЫЕ ДАННЫЕ
Рассчитать моду.
Определить медиану.
Распределение начальной пластовой температуры по
месторождениям в регионе N.
ОПРЕДЕЛИТЬ и СДЕЛАТЬ ВЫВОД ПО ПОЛУЧЕННЫМ
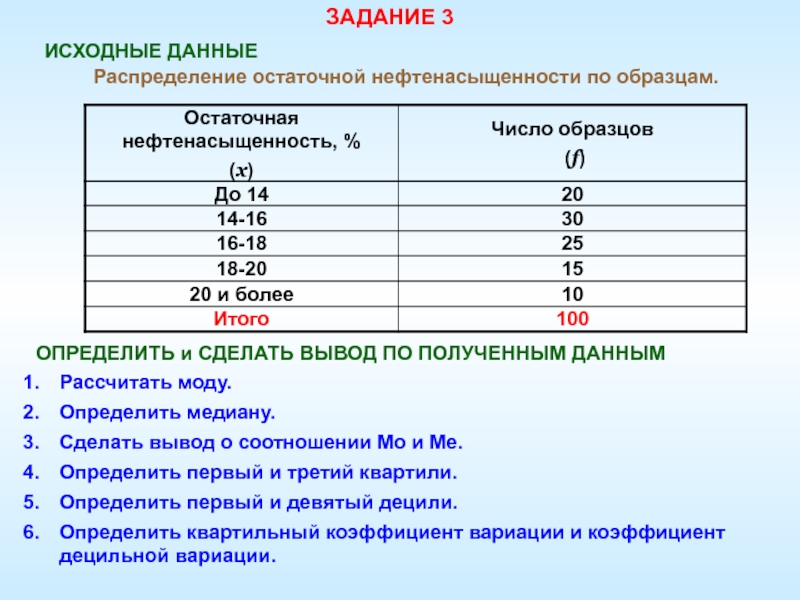
ДАННЫМСлайд 93ЗАДАНИЕ 3
ИСХОДНЫЕ ДАННЫЕ
Распределение остаточной нефтенасыщенности по образцам.
ОПРЕДЕЛИТЬ и СДЕЛАТЬ
ВЫВОД ПО ПОЛУЧЕННЫМ ДАННЫМ
Рассчитать моду.
Определить медиану.
Сделать вывод о соотношении
Мо и Ме.Определить первый и третий квартили.
Определить первый и девятый децили.
Определить квартильный коэффициент вариации и коэффициент децильной вариации.
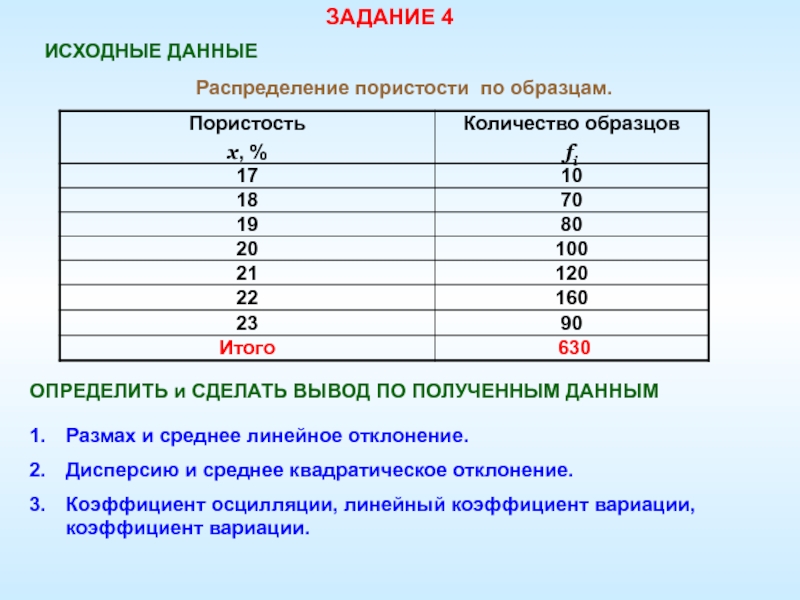
Слайд 94ЗАДАНИЕ 4
ИСХОДНЫЕ ДАННЫЕ
Распределение пористости по образцам.
ОПРЕДЕЛИТЬ и СДЕЛАТЬ ВЫВОД
ПО ПОЛУЧЕННЫМ ДАННЫМ
Размах и среднее линейное отклонение.
Дисперсию и среднее квадратическое
отклонение. Коэффициент осцилляции, линейный коэффициент вариации, коэффициент вариации.