Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция1_Классификация_многомерных и_ одномерные.ppt
Содержание
- 1. Лекция1_Классификация_многомерных и_ одномерные.ppt
- 2. 08/13/2019Тема1. Основные понятия и классификация методов
- 3. 08/13/2019ЗадачиГлавной целью большинства выполняемых на компьютере расчетов
- 4. 08/13/2019Модели задач выбора В каждом случае при
- 5. 08/13/2019Критерии вышеприведенных примеров:
- 6. 08/13/2019Постановка задачи о локальном минимумеПусть в Евклидовом
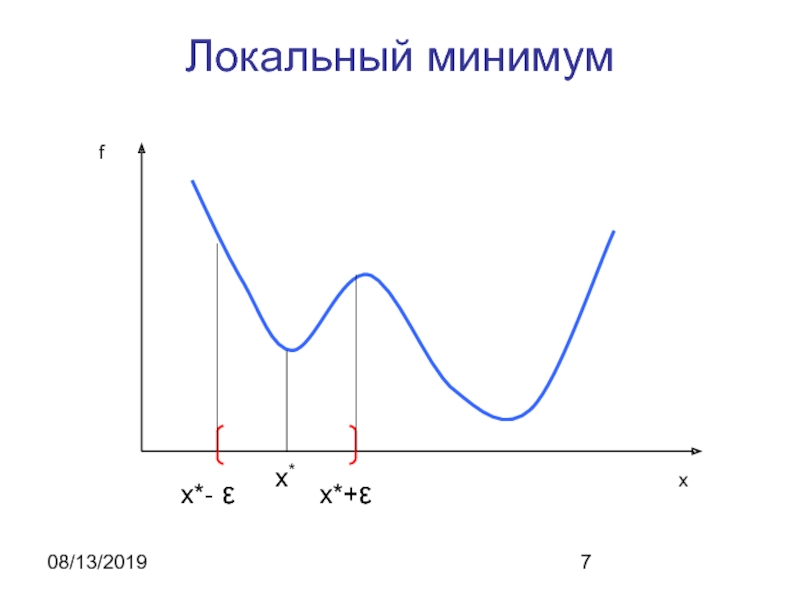
- 7. 08/13/2019Локальный минимумx*x*- εx*+εxf
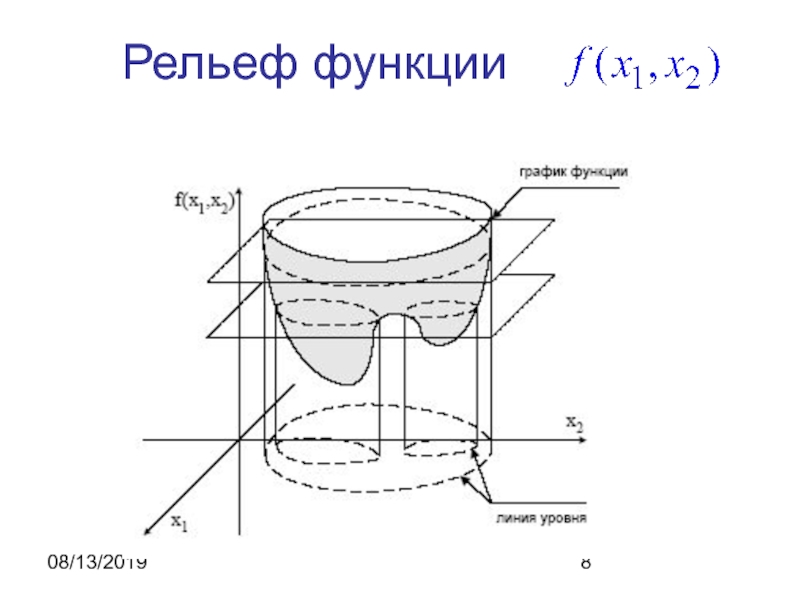
- 8. 08/13/2019Рельеф функции
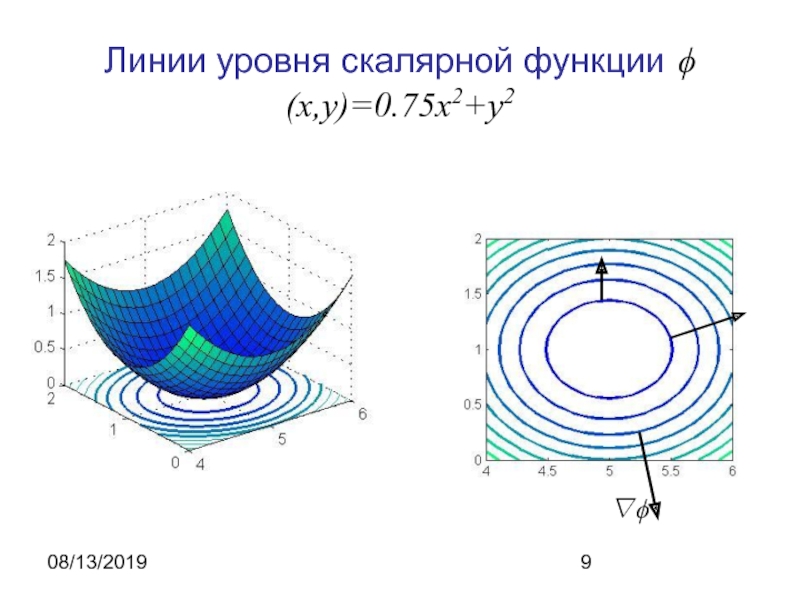
- 9. 08/13/2019Линии уровня скалярной функции ϕ(x,y)=0.75x2+y2∇ϕ
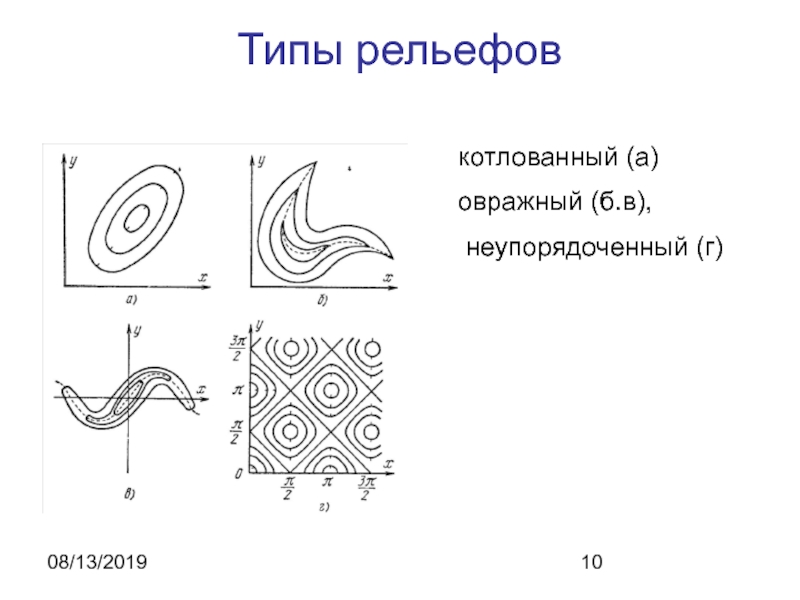
- 10. 08/13/2019Типы рельефовкотлованный (а)овражный (б.в), неупорядоченный (г)
- 11. 08/13/2019Общая характеристика методов многомерной оптимизацииПрактически все методы
- 12. 08/13/2019x1x2dz
- 13. 08/13/2019Спуск по выбранному направлениюЕсли
- 14. 08/13/2019Задача
- 15. 08/13/2019Все многообразие методов минимизации функции n переменных
- 16. 08/13/2019Классификация методов многомерной оптимизацииМЕТОДЫ НУЛЕВОГО ПОРЯДКА -
- 17. 08/13/2019МЕТОДЫ НАХОЖДЕНИЯ МИНИМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙНаиболее часто
- 18. 08/13/2019Метод последовательного перебора (MPP) Идея этого метода
- 19. 08/13/2019Метод последовательного перебора (MPP)x0hxY=ϕ(x)
- 20. 08/13/2019Метод последовательного перебораЗадаются x0, некоторый шаг h
- 21. 08/13/2019Метод последовательного перебора
- 22. 08/13/2019Метод квадратичной параболы (MP2) Для ускорения спуска
- 23. 08/13/2019Вблизи точки x0 выбираются три точки x1,
- 24. 08/13/2019
- 25. 08/13/2019Конец
- 26. Скачать презентанцию
08/13/2019Тема1. Основные понятия и классификация методов многомерной оптимизацииПостановка задачи Рельеф функции Классификация методов многомерной оптимизации Методы нахождения минимума функции одной переменной
Слайды и текст этой презентации
Слайд 208/13/2019
Тема1.
Основные понятия и классификация методов многомерной оптимизации
Постановка задачи
Рельеф
функции
переменнойСлайд 308/13/2019
Задачи
Главной целью большинства выполняемых на компьютере расчетов является принятие оптимального
в конкретной ситуации решения или, что тоже самое, сделать наилучший
выбор из множества допустимых вариантов:сколько и куда вложить денег, чтобы получить наибольшую прибыль
по какой дороге поехать, чтобы сэкономить бензин, время и при этом обеспечить безопасность
как выбрать параметры прибора, что бы при его минимальной стоимости изготовления достигался максимум КПД.
Слайд 408/13/2019
Модели задач выбора
В каждом случае при решении задачи выбора
требуется построить математическую модель, описывающую конкретную ситуацию
Формулировка модели содержит
некоторое количество параметров значение которых определяет конкретный вариант
Ценность каждого варианта определяется числом, которое называется критерием.
Если удается сопоставить каждому варианту определенное значение критерия то получаем целевую функцию
Слайд 508/13/2019
Критерии вышеприведенных примеров:
- величина прибыли при вложениях x1..xn
- длина дороги через пункты x1..xk- величина КПД при значениях x1..xn
В результате, задача принятия оптимального решения приводит к нахождению оптимального (максимального или минимального) значения
Следует отметить, что нахождение максимума
эквивалентно нахождению минимума
поэтому стандартные программы разрабатываются, как правило, для нахождения
Слайд 608/13/2019
Постановка задачи о локальном минимуме
Пусть в Евклидовом пространстве задана функция
Говорят,
что имеет локальный минимум в
точкеесли существует некоторая ε-окрестность точки , в которой выполняется
Будем полагать, что непрерывная дважды дифференцируемая функция.
Слайд 1108/13/2019
Общая характеристика методов многомерной оптимизации
Практически все методы минимизации функции n
переменных основаны на многократном повторении следующих двух действий:
выбор в области
параметров некоторого направления спуска;спуск к минимуму вдоль выбранного направления.
Слайд 1308/13/2019
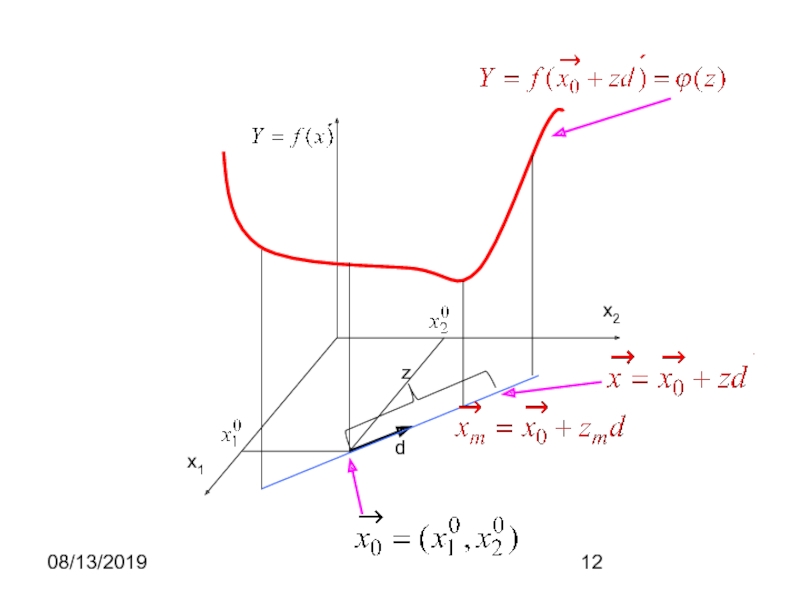
Спуск по выбранному направлению
Если -
единичный вектор выбранного направления в точке ,
то уравнение прямой, проходящей через эту точку в направлении , записывается в видегде параметр z , соответствующий точкам на прямой (модуль z есть расстояние от текущей точки до ).
Значения функции вдоль этой прямой можно описать функцией одной переменной
Изменяя z двигаемся вдоль этой прямой, находим точку , в которой функция имеет меньшее значение, чем в точке
Обычно находим минимум функции одной переменной
Слайд 1408/13/2019
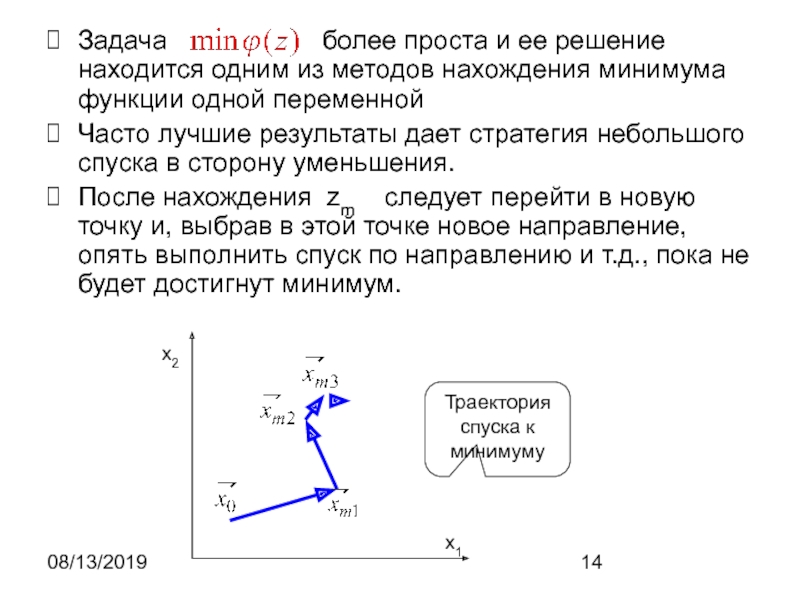
Задача
более проста и ее решение находится одним из методов
нахождения минимума функции одной переменнойЧасто лучшие результаты дает стратегия небольшого спуска в сторону уменьшения.
После нахождения zm следует перейти в новую точку и, выбрав в этой точке новое направление, опять выполнить спуск по направлению и т.д., пока не будет достигнут минимум.
x1
x2
Траектория спуска к минимуму
Слайд 1508/13/2019
Все многообразие методов минимизации функции n переменных определяется множеством способов
выбора направлений и методов спуска в выбранном направлении.
Слайд 1608/13/2019
Классификация методов многомерной оптимизации
МЕТОДЫ НУЛЕВОГО ПОРЯДКА - при выборе направления
спуска требуют вычисления только значений функции (методы: Гаусса-Зейделя, Пауэлла, ДСК,
Розенброка, Хука-Дживса, Нелдера-Мида).МЕТОДЫ ПЕРВОГО ПОРЯДКА - требуют вычисления (точного или приближенного) градиента функции (методы: градиентный, сопряженных градиентов, Давидона-Флетчера-Пауэлла (ДФП), Флетчера-Ривса и др.).
МЕТОДЫ ВТОРОГО ПОРЯДКА - требуют вычисления как градиента, так и матрицы вторых производных (методы: Ньютона, Ньютона-Рафсона).
МЕТОДЫ С ПЕРЕМЕННОЙ МЕТРИКОЙ – занимают промежуточное место между методами 1-го и 2-го порядка.
Слайд 1708/13/2019
МЕТОДЫ НАХОЖДЕНИЯ МИНИМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Наиболее часто используемые методы можно
разбить на два класса:
1) методы уточнения минимума на заданном интервале
[a, b] (метод деления пополам, метод золотого сечения);2) методы спуска к минимуму из некоторой начальной точки x0 (метод последовательного перебора, метод квадратичной параболы, метод кубической параболы).
Ниже рассмотрим только методы спуска
Слайд 1808/13/2019
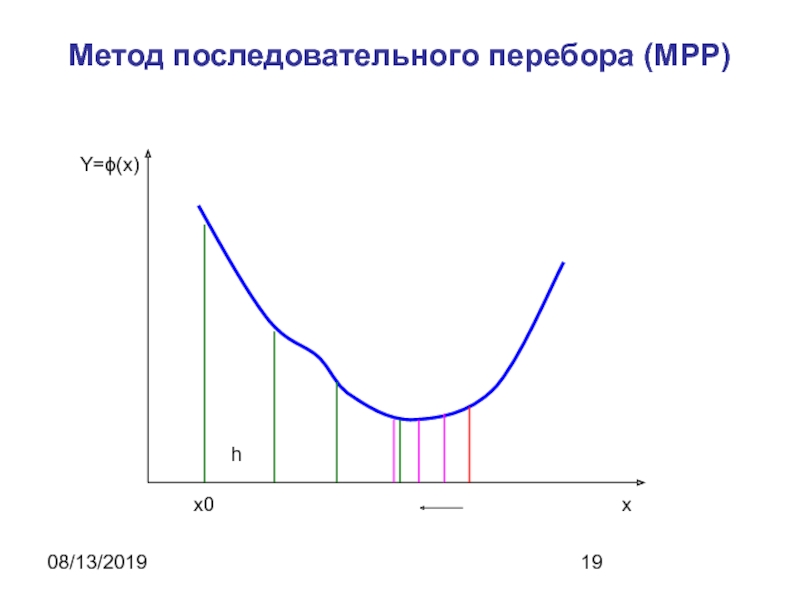
Метод последовательного перебора (MPP)
Идея этого метода состоит в том,
что, спускаясь из точки x0 с заданным шагом h в
направлении уменьшения функции, устанавливают интервал длиной h, на котором находится минимум, и затем его уточняют.Уточнение можно осуществить либо методом золотого сечения, либо повторяя спуск с последней точки, уменьшив шаг и изменив его знак.
Алгоритм последнего варианта приведен ниже
Слайд 2008/13/2019
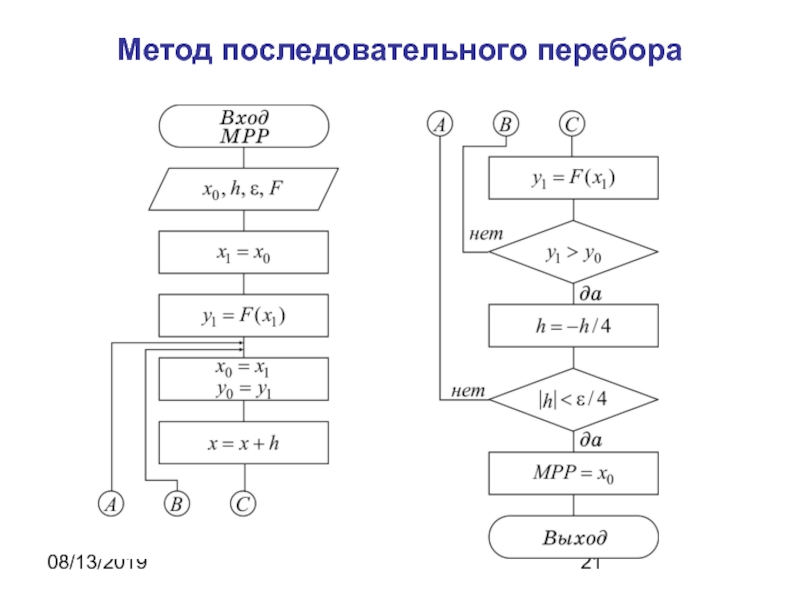
Метод последовательного перебора
Задаются x0, некоторый шаг h и погрешность ε
.
1. В точке x0 вычисляется x1=x0 и y1=f(x1).
2. x0=x1,
y0=y1 - запоминается удачная точка.3. x1=x0+h, y1=f(x1) - делаем следующий шаг в удачном направлении.
4. Если функция убывает, y1
5. h=-h/4. В точке x1 функция оказалась большей, чем в x0, следовательно, мы перешагнули точку минимума и организуем спуск в обратном направлении.
6. Если , тогда повторить с п.2, иначе перейти к п.7.
7. конец.
Слайд 2208/13/2019
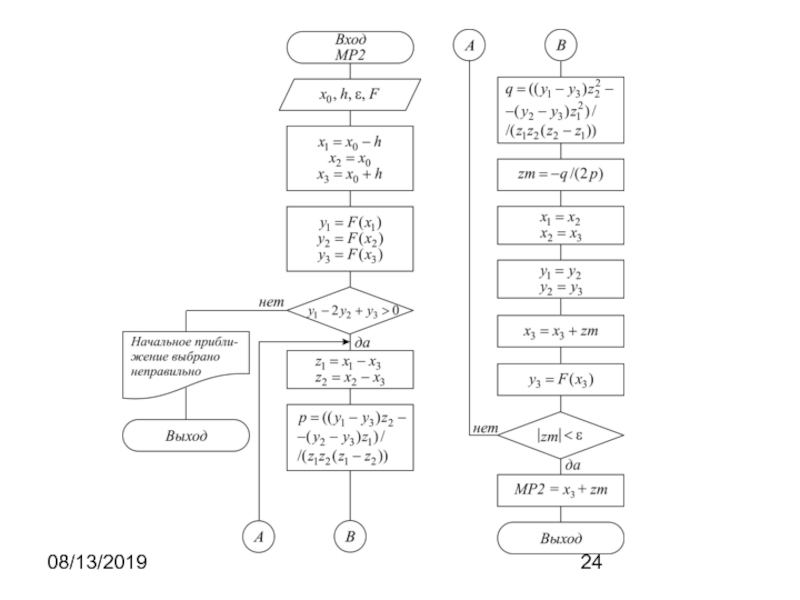
Метод квадратичной параболы (MP2)
Для ускорения спуска к минимуму из
некоторой точки x0 используют локальные свойства функции вблизи этой точки.
Так, скорость и направление убывания можно определить по величине и знаку первой производной.
Вторая производная характеризует направление выпуклости: если f''>0, то функция имеет выпуклость вниз, иначе - вверх.
Вблизи локального безусловного минимума дважды дифференцируемая функция всегда выпукла вниз.
Поэтому, если вблизи точки минимума функцию аппроксимировать квадратичной параболой, то она будет иметь минимум. Это свойство и используется в методе квадратичной параболы
Слайд 2308/13/2019
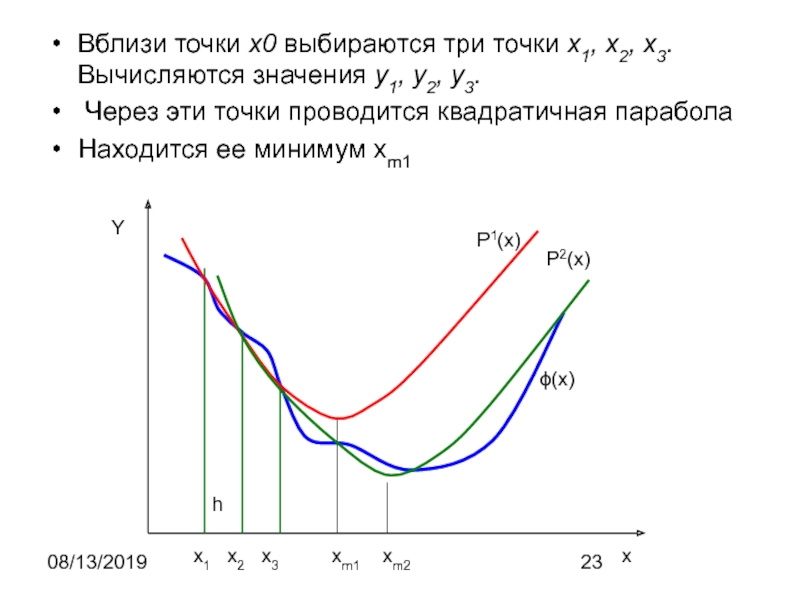
Вблизи точки x0 выбираются три точки x1, x2, x3. Вычисляются
значения y1, y2, y3.
Через эти точки проводится квадратичная парабола
Находится
ее минимум xm1x1 x2 x3
h
x
Y
ϕ(x)
xm1
P1(x)
P2(x)
xm2