и примерами их практического применения.
План лекции
Введение
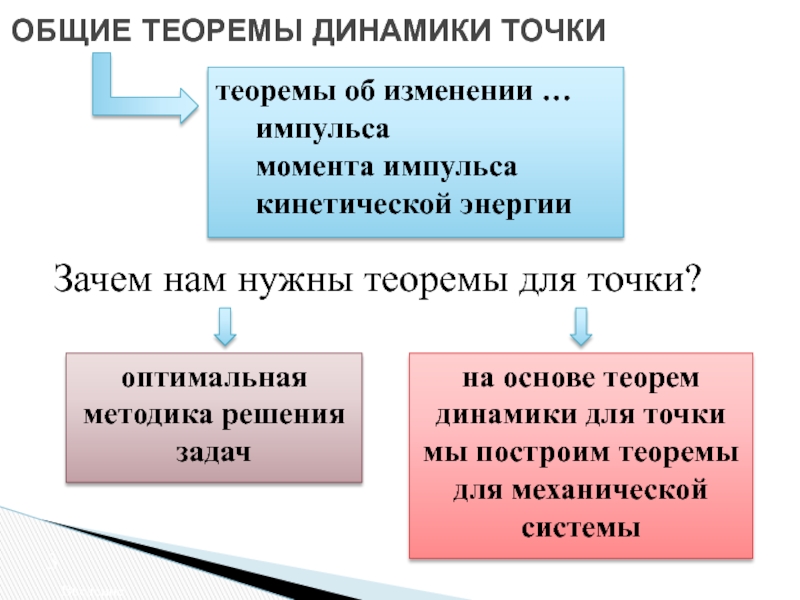
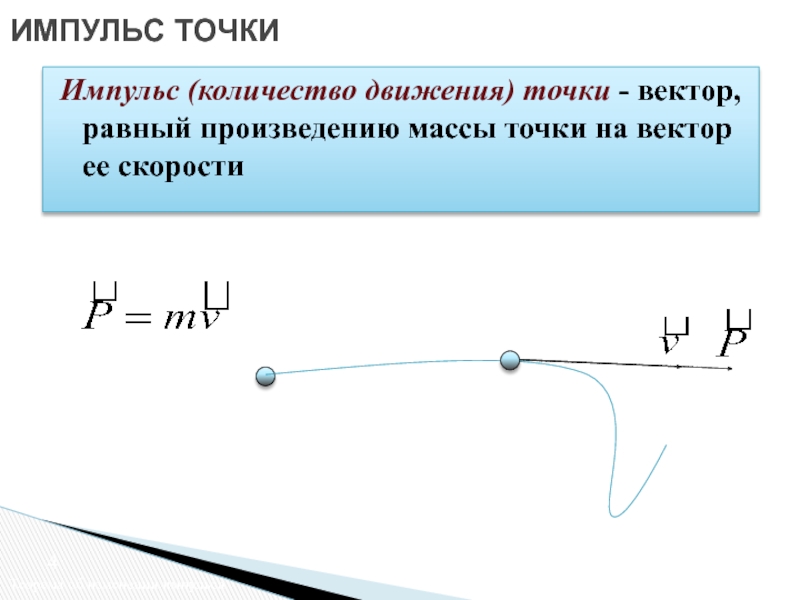
Теорема об изменении импульса
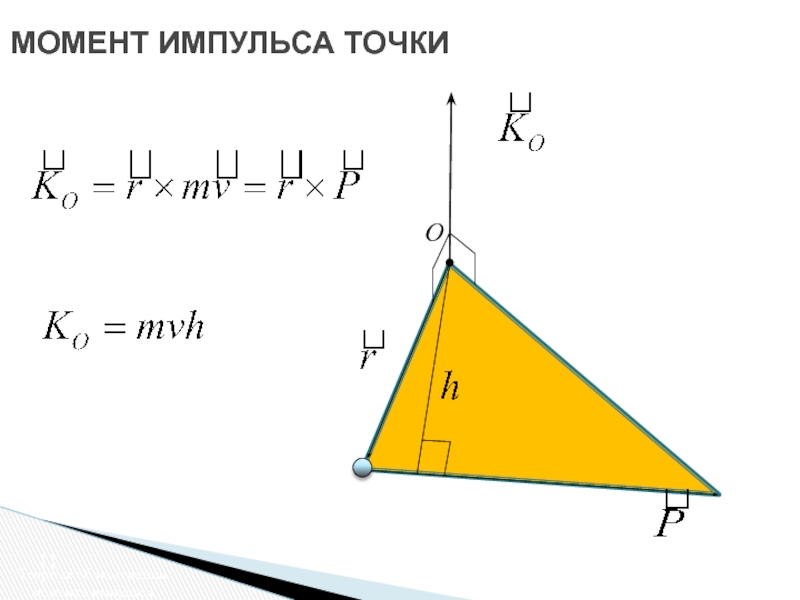
точки Теорема об изменении момента импульса точки
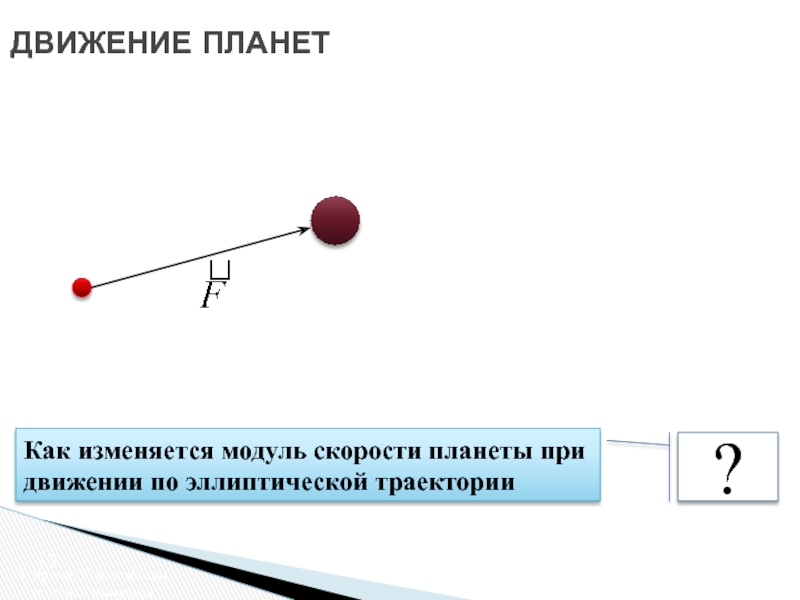
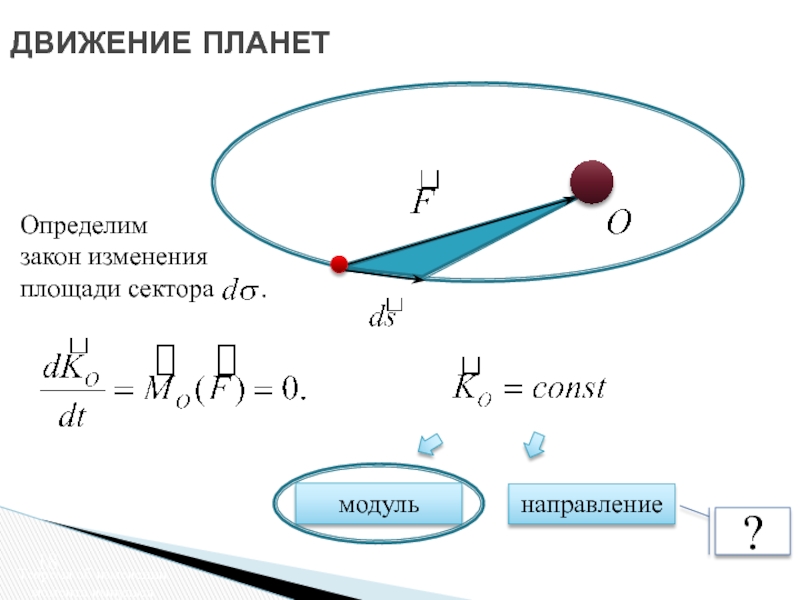
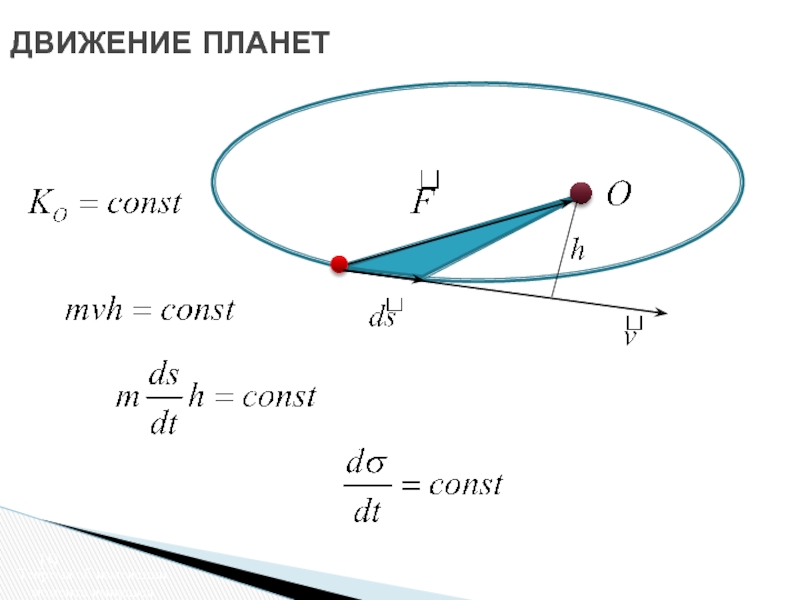
Движение в центральном поле
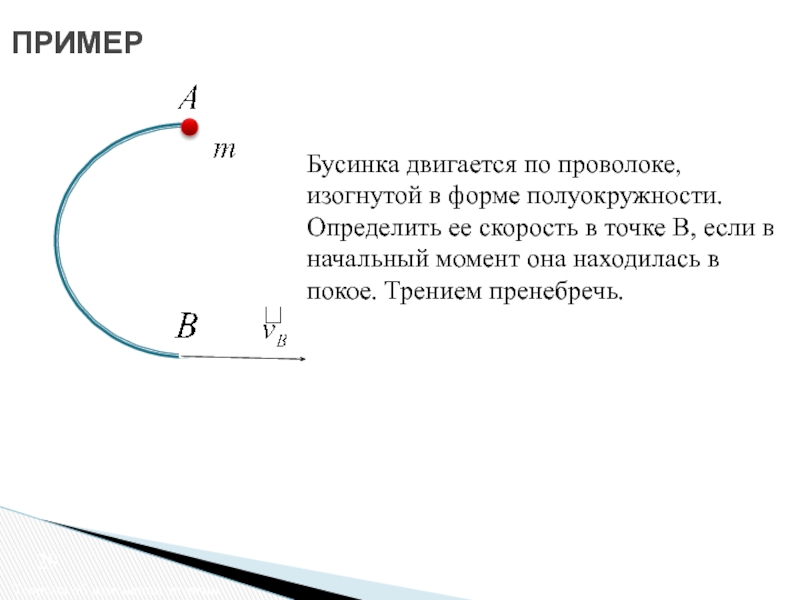
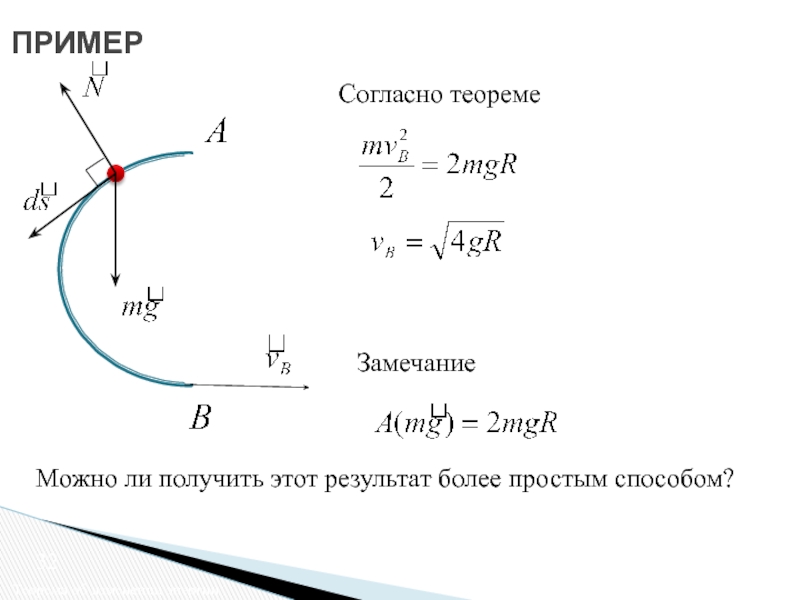
Теорема об изменении кинетической энергии точки
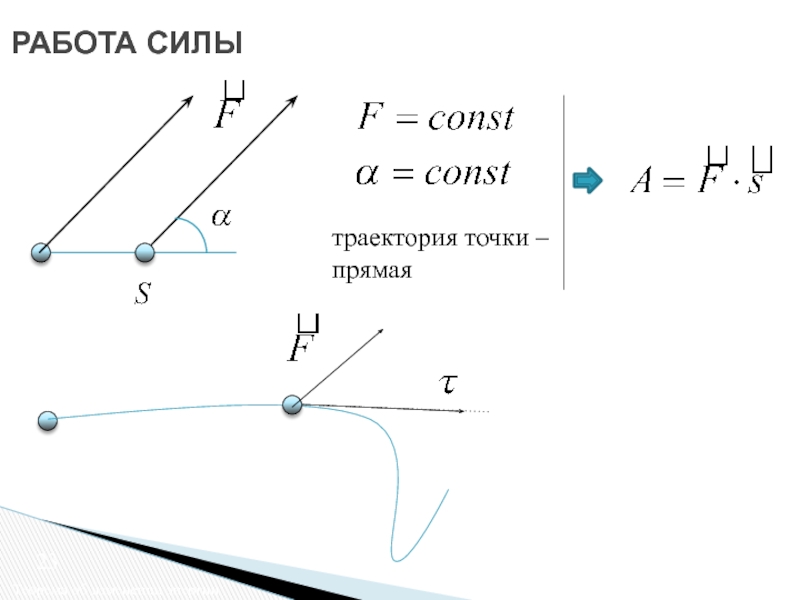
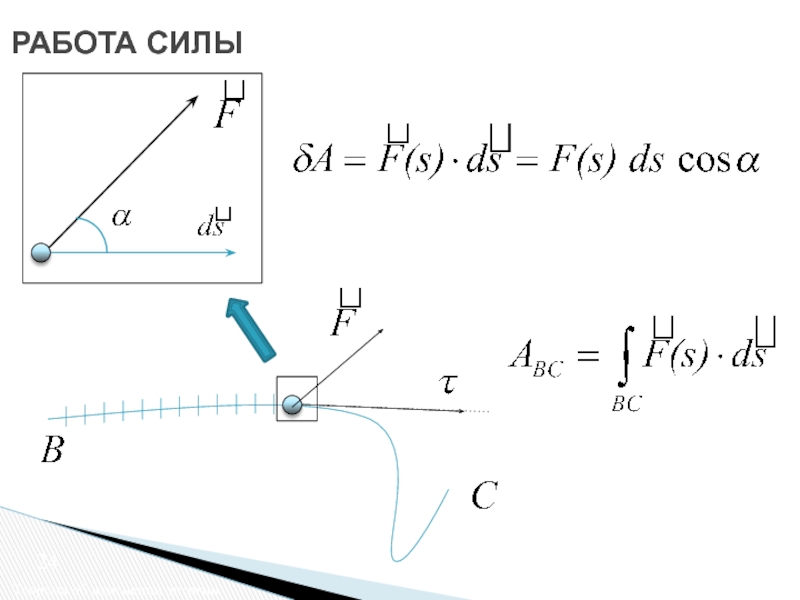
Работа силы. Потенциальные силы
Заключение