Слайд 1Лекция 16
1. Механика жидкостей и газов
2. Специальная теория относительности
Слайд 21. Механика жидкостей и газов
Основным отличием жидкостей от твердых
(упругих) тел является способность легко изменять свою форму. Поэтому жидкость
принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы.
На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил вводится физическая величина – давление.
Давление определяется как отношение модуля силы F, действующей перпендикулярно поверхности, к площади S этой поверхности: p = F/S
В системе СИ давление измеряется в паскалях (Па): 1 Па = 1 Н/м2
Часто используются внесистемные единицы: нормальная атмосфера (атм) и миллиметр ртутного столба (мм Hg): 1 атм = 101325 Па = 760 мм Нg
Французский ученый Б.Паскаль в середине XVII века эмпирически установил закон, названный законом Паскаля: Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.
Слайд 3Для иллюстрации закона Паскаля рассмотрим прямоугольную призму, погруженную в жидкость.
Если предположить, что плотность материала призмы равна плотности жидкости, то
призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т.е. силы, действующие на единицу поверхности каждой грани, одинаковы: p1 = p2 = p3 = p.
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты h и площади основания S равна весу столба жидкости mg, где m = ρghS – масса жидкости в сосуде, ρ – плотность жидкости. Следовательно
Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Давление столба жидкости ρgh называют гидростатическим давлением.
Слайд 4Если жидкость находится в цилиндре под поршнем, то действуя на
поршень некоторой внешней силой F, можно создавать в жидкости дополнительное
давление p0 = F / S, где S – площадь поршня.
Таким образом, полное давление в жидкости на глубине h можно записать в виде: p = p0 + ρgh.
Из-за разности давлений в жидкости на разных уровнях возникает выталкивающая или архимедова сила FA.
Поясним появление архимедовой силы.
В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S. Разность давлений на нижнюю и верхнюю грани есть: Δp = p2 – p1 = ρgh.
Поэтому выталкивающая сила FA будет направлена вверх, и ее модуль равен FA = F2 – F1 = SΔp = ρgSh = ρgV, где V – объем вытесненной телом жидкости, а ρV – ее масса.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.
Слайд 5Из закона Архимеда вытекает, что если средняя плотность тела ρт
больше плотности жидкости (или газа) ρ, тело будет опускаться на
дно. Если же ρт < ρ, тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Из выражения для полного давления в жидкости p = p0 + ρgh вытекает, что в сообщающихся сосудах любой формы, заполненных однородной жидкостью, давления в любой точке на одном и том же уровне одинаковы.
Слайд 6Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то
с помощью внешних сил, приложенных к поршням, в жидкости можно
создать большое давление р, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление р.
Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют разные силы F1 = pS1 и F2 = pS2. Если S2 >> S1, то F2 >> F1. Устройства такого рода называют гидравлическими машинами. Выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным: F1h1 = F2h2.
Это правило выполняется для любых идеальных машин, в которых не действуют силы трения. Оно называется «золотым правилом механики».
Гидравлические машины, используемые для подъема грузов, называются домкратами. Они широко применяются также в качестве гидравлических прессов. В качестве жидкости обычно используются минеральные масла.
Слайд 7Элементы гидро- и аэродинамики
Движение жидкостей или газов представляет собой
сложное явление. Для его описания жидкость (или газ) предполагаются несжимаемыми
и идеальными (т.е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли (1738 г.). Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах.
Слайд 8За промежуток времени Δt жидкость в трубе сечением S1 переместится
на l1 = υ1Δt, а в трубе сечением S2 – на l2 = υ2Δt,
где υ1 и υ2 – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде: ΔV = l1S1 = l2S2 или υ1S1 = υ1S1. Здесь ΔV – объем жидкости, протекшей через сечения S1 и S2.
Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т.е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления - это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.
Так как жидкость предполагается идеальной, она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.

Слайд 9При перемещении жидкости силы давления совершают работу: ΔA = p1S1l1 – p2S2l2 = p1S1υ1Δt – p2S2υ2Δt = (p1 – p2)ΔV.
Работа ΔA сил
давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с
обратным знаком.
Изменения, произошедшие за время Δt в выделенной части жидкости, заключенной между сечениями S1 и S2 в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δm = ρΔV (ρ – плотность жидкости) из одной части трубы сечением S1 в другую часть сечением S2. Закон сохранения механической энергии для этой массы имеет вид: E2 – E1 = ΔA = (p1 – p2)ΔV, где E1 и E2 – полные механические энергии массы Δm в поле тяготения:
Отсюда следует:
Это и есть уравнение Бернулли. Из него следует, что сумма
остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h1 = h2) уравнение Бернулли принимает вид:
Слайд 10Величина p – статическое давление в жидкости. Оно может быть
измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление
в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости. Из уравнения Бернулли следует:
Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.
Слайд 11Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует
применять к линиям тока, т.е. линиям, вдоль которых перемещаются частицы
жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие.
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:
где p0 – атмосферное давление, h – перепад высоты вдоль линии тока. Таким образом,
Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.
Слайд 12Уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.
Одной
из таких задач является изучение сил, действующих на крыло самолета.
Уравнение Бернулли позволяет дать качественное объяснение возникновению подъемной силы крыла.
Из-за специального профиля крыла и наличия угла атаки, т.е. угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила F, действующая на крыло. Вертикальная составляющая Fy этой силы называется подъемной силой. Она позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая Fx представляет собой силу сопротивления среды.
Слайд 13Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося
тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха,
вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
Итак, во многих явлениях аэродинамики существенную роль играют силы вязкого трения. Они приводят к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не учитывает сил трения. Его вывод основан на законе сохранения механической энергии при течении жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения.
Слайд 142. Основы специальной теории относительности
Постулаты специальной теории относительности Эйнштейна
1.
Принцип относительности: Все законы природы одинаковы во всех инерциальных системах
отсчета
2. Принцип постоянства скорости света: Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света c = 2,9979246·108 м/с ≈ 3·108 м/с
Преобразования координат и времени
Слайд 15(1) При t = t' = 0 начала координат обеих
систем совпадают: x0 = x'0 = 0
(2)
x0 = v0·t (2') x'0 = – v0·t'
Чтобы выполнялись (1) и (2), для любой точки должно быть:
(3) x = γ·(x' + v0·t') (3') x' = γ·(x – v0·t)
Пусть при t = t' = 0 в начале координат произойдет вспышка света. После этого будет двигаться «фронт световой волны» - граница светлой и темной зон пространства.
Поскольку системы координат равноправны, а скорость света одинакова в обеих системах координат, то координата «фронта»:
(4) x = c·t; (4') x' = c·t'
(3) x = γ·(x' + v0·t') (3') x' = γ·(x – v0·t)
(4) x = c·t; (4') x' = c·t'
(5) c·t = γ·(c·t' + v0·t') (5') c·t' = γ·(c·t – v0·t)
Вынесем за скобки время и перемножим (5) и (5')
c2 = γ2·(c2 – v02)
γ = 1/(1 – v02/c2)1/2
Слайд 17Относительность одновременности
Два события в нештрихованной системе отсчета происходят одновременно,
но в точках с разными координатами x.
В штрихованной системе
отсчета они произойдут в разное время t'.
Слайд 18Относительность длины
Рассмотрим стержень, неподвижный в нештрихованной системе отсчета. Его
длина Δx = xконца – xначала
Если в штрихованной системе отсчета
(где стержень движется) одновременно (t'=const) замерить x'конца и x'начала, то с учетом, что
Слайд 19Относительность промежутка времени
Слайд 20Интервал
Что не меняется при переходе из одной системы отсчета
в другую?
Из преобразований Лоренца можно получить
c2·t2 - x2 - y2
- z2 = c2·t′2 - x′2 - y′2 - z′2
Эта величина называется интервал s
s2 > 0 s – действительное число интервал времениподобный, может разделять события, имеющие причинно-следственную связь
s2 = 0 s = 0 интервал светоподобный: движение луча света
s2 < 0 s – мнимое число интервал пространственноподобный, не может разделять события, имеющие причинно-следственную связь
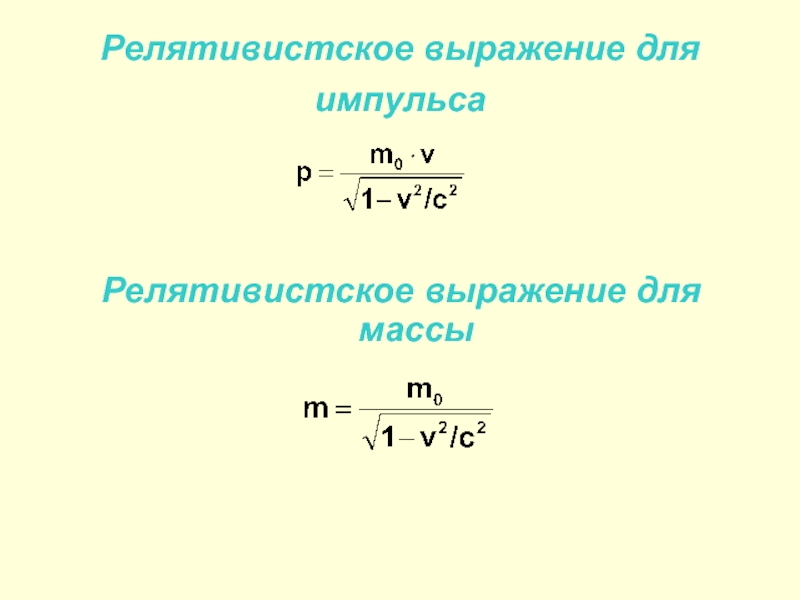
Слайд 22Релятивистское выражение для импульса
Релятивистское выражение для массы
Слайд 23Релятивистское выражение для энергии
Сила
E=mc2 – полная энергия
Слайд 24Взаимосвязь энергии и импульса
E=mc2 ; p=mv
- эта разность не меняется при переходе от одной системы координат к другой – она инвариантна относительно преобразования системы координат.