Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 16
Содержание
- 1. Лекция 16
- 2. 11.1. Основные понятия и определения СП Вещественную
- 3. называть случайным процессом; случайную величину Хt –
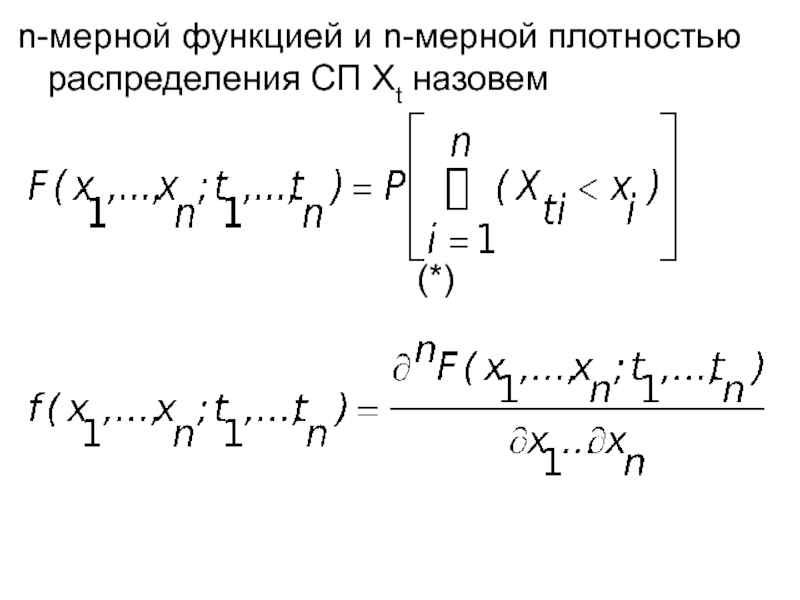
- 4. n-мерной функцией и n-мерной плотностью распределения СП Хt назовем (*)
- 5. Множество всех конечномерных законов распределения (*) будем
- 6. – центрированный СП. Ковариационным и корреляционным моментами СП Хt называются функции (2)
- 7. Нормированной корреляционной функцией сечений Хt, Хt’ СП
- 8. Если X(t) и Y(t) – два СП,
- 9. Теорема: СП X(t) является гильбертовым тогда и
- 10. СП X(t) называется непрерывным: почти наверное (п.н.), если
- 11. Каноническим разложением СП X(t) называют его представление
- 12. 11.2. Основные понятия и определения стационарных СПСП
- 13. m(t)= mx(0)=const, D(t)=K(t, t)=K(0,0)=const, K(t, t’)=K(t-t’,0)=K(0, t’-t).
- 14. 11.3. Спектральное разложение стационарных СП - стационарный СП,
- 15. (k=1, 2,…) (5) координатные функции cos kt, sin
- 16. М(Uk)=М(Vk)=0, D(Uk)=D(Vk)=Dk, М(Ui Uj)=М(Vi Vj)=0, M(Vi Uj)=0
- 17. Множество пар {(k, Dk)} называют спектром дисперсий
- 18. M[U()]=M[V()]=0, KU(,’)=M[U()U(’)]=s()( - ’),
- 19. (11)s() и k() спектральная функция.
- 20. Термин «шум» обозначает нежелательные электрические сигналы, которые
- 21. электромагнитного излучения (искровое зажигание). Естественные шумы исходят
- 22. процесс с нулевым средним. Основной спектральной характеристикой
- 23. но ни один случайный процесс в действительности
- 24. Скачать презентанцию
11.1. Основные понятия и определения СП Вещественную переменную t будем называть временем; вещественную функцию x(t) – процессом; график функции x(t) – траекторией процесса. Множество возможных значений t обозначим Т. Пусть Xt
Слайды и текст этой презентации
Слайд 3называть случайным процессом; случайную величину Хt – сечением случайного процесса
в момент времени t. Реализацию сечения Хt будем обозначать хt
или x(t). В соответствии с определением случайных величин x(t)=X(t, ), где . Функцией распределения сечения Хt называют одномерной функцией распределения случайного процесса (СП) и обозначают F(x; t)=P(ХtСлайд 5Множество всех конечномерных законов распределения (*) будем называть законом распределения
СП Хt. Математическим ожиданием, дисперсией и средним квадратическим отклонением СП
Хt будем называть функции (1)Слайд 7Нормированной корреляционной функцией сечений Хt, Хt’ СП Хt будем называть
функцию
Числовые характеристики получены для СВ Хt и Хt’ - сечений
СП, то операции M, D, R, K, обладают свойствами, установленными в теоремах о числовых характеристиках СВ и векторов Слайд 8Если X(t) и Y(t) – два СП, определенные на {,
F, P} и Т, то их взаимной корреляционной функцией будем
называтьСП X(t) называют гильбертовым, если существует для любого tT
Слайд 9Теорема: СП X(t) является гильбертовым тогда и только тогда, когда
существует R(t, t’) для всех (t, t’)ТТ.
Множество Т может
быть дискретным и континуальным. В первом случае СП Хt называют процессом с дискретным временем, во втором – с непрерывным временем. СП X(t) называется выборочно непрерывным, дифференцируемым и интегрируемым в точке , если его реализация x(t)=x(t, ) соответственно непрерывна, дифференцируема и интегрируема.
Слайд 10СП X(t) называется непрерывным:
почти наверное (п.н.), если Р(А)=1
в среднем
квадратическом (с.к.), если
по вероятности (п.в.), если
Слайд 11Каноническим разложением СП X(t) называют его представление в виде
где
Vi – коэффициенты – СВ с характеристиками M(Vi )=0, D(Vi)=
Di,M(Vi Vj)=0, которые называют элементарными; а i(t) – координатные функции канонического разложения процесса X(t).
Слайд 1211.2. Основные понятия и определения стационарных СП
СП X(t) называют стационарным
в узком смысле, если F(x1,…,xn; t1,…,tn)= F(x1,…,xn; t1 +,…, tn
+) при произвольных n1, x1,…,xn, t1,…,tn, ; t1 , ti+ T. Здесь F(x1,…,xn; t1,…,tn) – n-мерная ФР СП X(t).СП X(t) называют стационарным в широком смысле, если m(t)=m(t+ ), K(t,t’)=K(t+, t’+) , t’+, t+, t, t’ T (3).
Для процесса, стационарного в широком смысле, можно записать
Слайд 13m(t)= mx(0)=const, D(t)=K(t, t)=K(0,0)=const, K(t, t’)=K(t-t’,0)=K(0, t’-t).
K(t,t’)=k()=k(- ),
=t’-t.
k() – четная функция, при этом k(0)=D=2; |k() |
k(0), D – дисперсия СП X(t). Слайд 1411.3. Спектральное разложение стационарных СП
- стационарный СП, определенный на отрезке
времени [0,T] с корреляционной функцией k(), определенной на отрезке
[-T,
T]. Поскольку k() – четная функция, то ее можно разложить в ряд Фурье (4)Слайд 15
(k=1, 2,…)
(5)
координатные функции cos kt, sin kt (k=0, 1,…)
и коэффициенты канонического разложения Uk, Vk (k=0, 1,…) с характеристиками
Слайд 16М(Uk)=М(Vk)=0, D(Uk)=D(Vk)=Dk,
М(Ui Uj)=М(Vi Vj)=0, M(Vi Uj)=0 (6)
(7)
Это выражение
называют дискретным спектральным разложением стационарного СП.
Полагая t’=t и учитывая
формулу K(t, t) =D[X(t)], найдем
Слайд 17Множество пар {(k, Dk)} называют спектром дисперсий спектрального разложения (4).
Если
Т=, то вместо дискретного применяется так называемое непрерывное или интегральное
каноническое разложение стационарного СП.(8)
U(), V() – случайные функции вещественной переменной : 0 с характеристиками
Слайд 18 M[U()]=M[V()]=0, KU(,’)=M[U()U(’)]=s()( - ’), (9)
KV(,’)=M[V()V(’)]=s()(
- ’), KUV(,’)=M[U()V()]=0
s() – некоторая вещественная функция, называемая спектральной
плотностью стационарного СП; () – функция Дирака; U(), V() – так называемые некоррелированные белые шумы с интенсивностью s(). (10)












![Лекция 16 11.3. Спектральное разложение стационарных СП - стационарный СП, определенный на отрезке времени 11.3. Спектральное разложение стационарных СП - стационарный СП, определенный на отрезке времени [0,T] с корреляционной функцией k(), определенной](/img/thumbs/04f85fb1799977bfdf2011f09c5e220a-800x.jpg)



![Лекция 16 M[U()]=M[V()]=0, KU(,’)=M[U()U(’)]=s()( - ’), (9) KV(,’)=M[V()V(’)]=s()( - ’), KUV(,’)=M[U()V()]=0 M[U()]=M[V()]=0, KU(,’)=M[U()U(’)]=s()( - ’), (9) KV(,’)=M[V()V(’)]=s()( - ’), KUV(,’)=M[U()V()]=0 s() – некоторая вещественная](/img/tmb/3/262951/673123bc2dd79b16e29c63849d0d2db9-800x.jpg)























