Лекция 2 Колебания связанных осцилляторов. Колебания молекул New

ряд
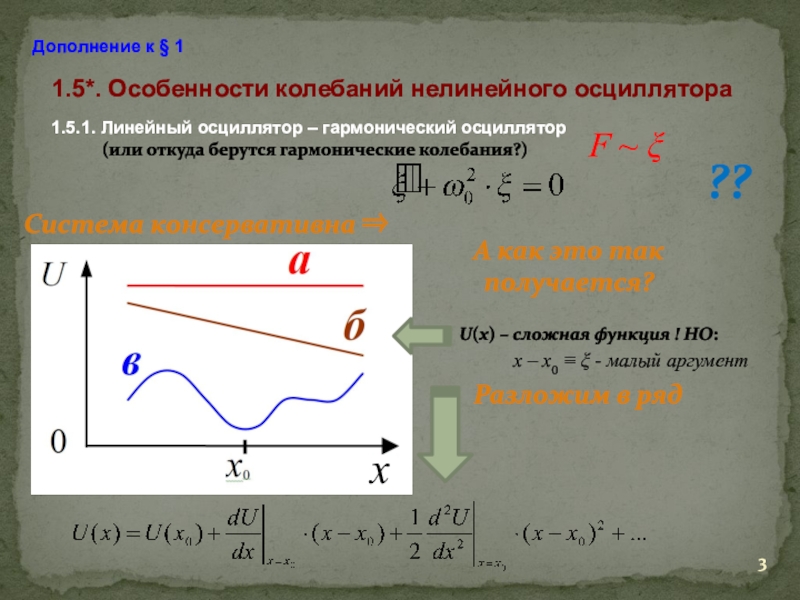
1.5.1. Линейный осциллятор – гармонический осциллятор
(или откуда берутся гармонические

А как это так получается?

U(x) – сложная функция ! НО:

F  

??

Система консервативна 

х

х – х0   - малый аргумент

A3cos(30t + 03) + …
f() = –k +

Неизохронность

Ангармонизм

! ??

 мала ! Тогда:

Но:

и тогда

«Возвращающая сила», линейный, гармонический осциллятор !!!

1.5.2. Нелинейный («ангармонический») осциллятор

Примеры: “Потенциал Морзе”, “Ленннард-Джонса” (6/12), “Бакингема”, …

 растёт  нельзя «аппроксимировать» параболой

колебаний нелинейного осциллятора

“Чаша”, …

Свободные колебания в системе связанных осцилляторов.
(о “модах” …)

m

1 = х1  х10

2 = х2  х20

– трения нет;
Все связи – квазиупругие – взаимодействуют линейные осцилляторы.

“Опр.” Нормальными координатами называются линейные комбинации исходных координат, которые позволяют свести систему уравнений к системе уравнений гармонических осцилляторов

А что же это за «моды» такие,
и как движутся сами атомы

Система уравнений и её решение: …

Частоты нормальных колебаний (мод)

??

“Биения”
2) Моды энергетически независимы !!
3) Несимметричные системы
??

“-/+”:
Синфазно
Противофазно

степени свободы молекул: 3N –

Внутримолекулярные колебания свободной двухатомной молекулы (Модель «гармонический осциллятор» в химии)

Пример 1. Изотопные сдвиги в колебательных спектрах

Пример 2. Свободные и связанные гидроксилы

??

Задачи 2.3 – 2.5 :

 = х2  х1  l0

Одна “колебательная степень свободы”

??

А где её “увидеть”

проверим

1650 см-1

1351 см-1
 3= 2396 см-1
Симметричная мода
Три фундаментальные моды молекулы СО2:

Антисимметричная мода

Деформационная мода