Слайд 1Лекция 25
Проекции с числовыми отметками
Принципы и аппарат проецирования
Проекции точки,
прямой, плоскости
Градуирование прямой
Понятия уклона и интервала прямой
Взаимное расположение прямых
Геометрическая модель
плоскости и способы ее задания. Масштаб уклона плоскости
Взаимное расположение точек , прямых и плоскостей
Проекции поверхностей
Слайд 2Проектирование и строительство жилых, общественных и промышленных зданий не может
осуществляться без инженерной подготовки и благоустройства городских территорий. Такие сооружения,
как магистрали и транспортные развязки, путепроводы и мосты, набережные и подземные переходы являются неотъемлемыми элементами современного города.
В процессе проектирования зданий и сооружений составляют чертежи, на которых изображается спланированная земная поверхность. Проектирование сооружений, чтение и выполнение чертежей требует знания специального способа изображения- метода проекций с числовыми отметками
Слайд 3Аппарат проецирования в проекциях с числовыми отметками
Если размеры проецируемого объекта
в вертикальном направлении малы по сравнению с размерами в горизонтальных
направлениях, целесообразно применять метод с числовыми отметками. Данный метод требует построение только одной проекции- на горизонтальную плоскость П, которую называют «нулевой» (за «абсолютный нуль» в нашей стране принят уровень Балтийского моря у Кронштадта).
С помощью метода с числовыми отметками изображается рельеф местности, нанесенные на нем дороги, а также решаются многие задачи по проектированию земляных сооружений, посадке объектов на рельеф, определению объема земляных работ и другие.
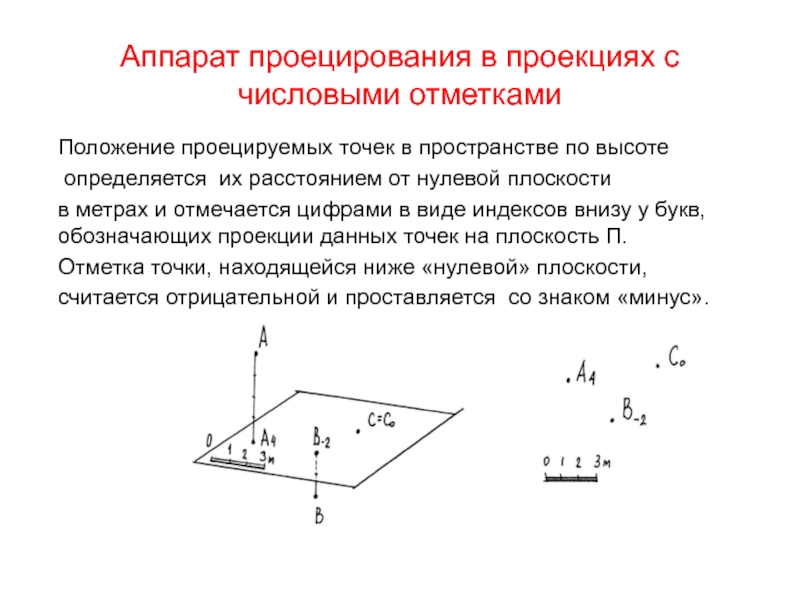
Слайд 4Аппарат проецирования в проекциях с числовыми отметками
Положение проецируемых точек в
пространстве по высоте
определяется их расстоянием от нулевой плоскости
в
метрах и отмечается цифрами в виде индексов внизу у букв, обозначающих проекции данных точек на плоскость П.
Отметка точки, находящейся ниже «нулевой» плоскости,
считается отрицательной и проставляется со знаком «минус».
Слайд 5Геометрическая модель прямой
Прямая может быть задана:
1. проекциями с числовыми отметками
двух ее точек
2. одной точкой с числовой отметкой, направлением горизонтальной
проекции этой прямой и тангенсом угла её наклона к плоскости По.
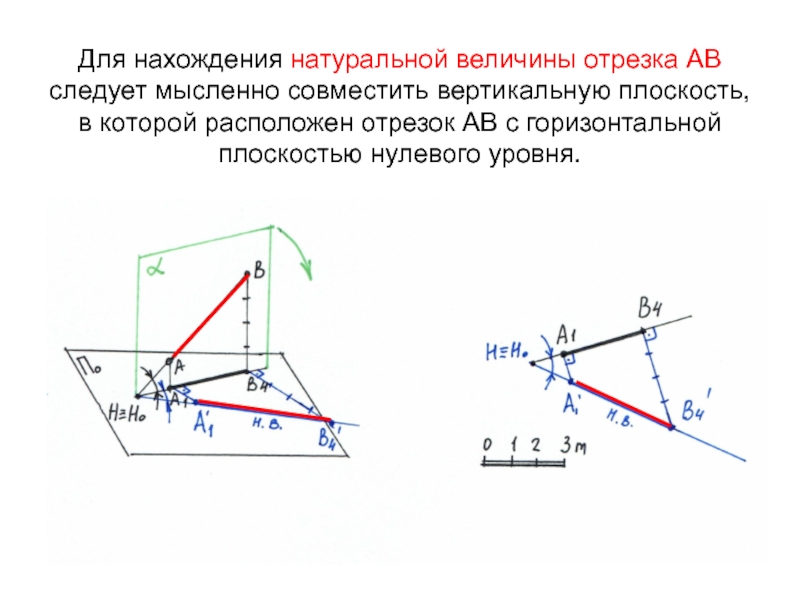
Слайд 6Для нахождения натуральной величины отрезка АВ следует мысленно совместить вертикальную
плоскость, в которой расположен отрезок АВ с горизонтальной плоскостью нулевого
уровня.
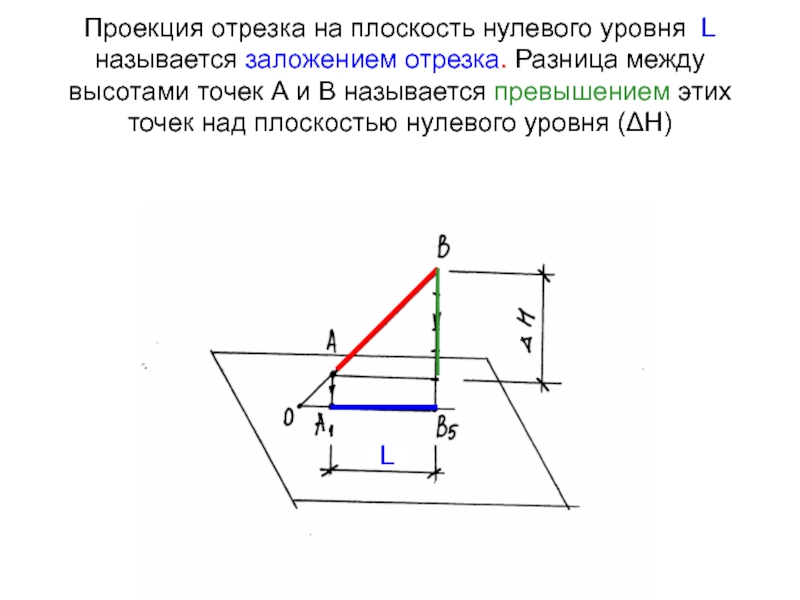
Слайд 7Проекция отрезка на плоскость нулевого уровня L называется заложением отрезка.
Разница между высотами точек А и В называется превышением этих
точек над плоскостью нулевого уровня (ΔΗ)
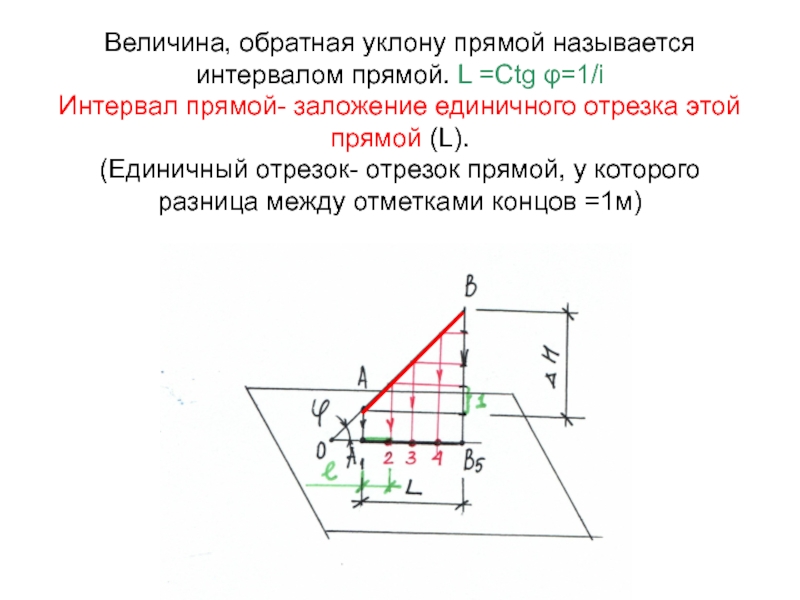
L
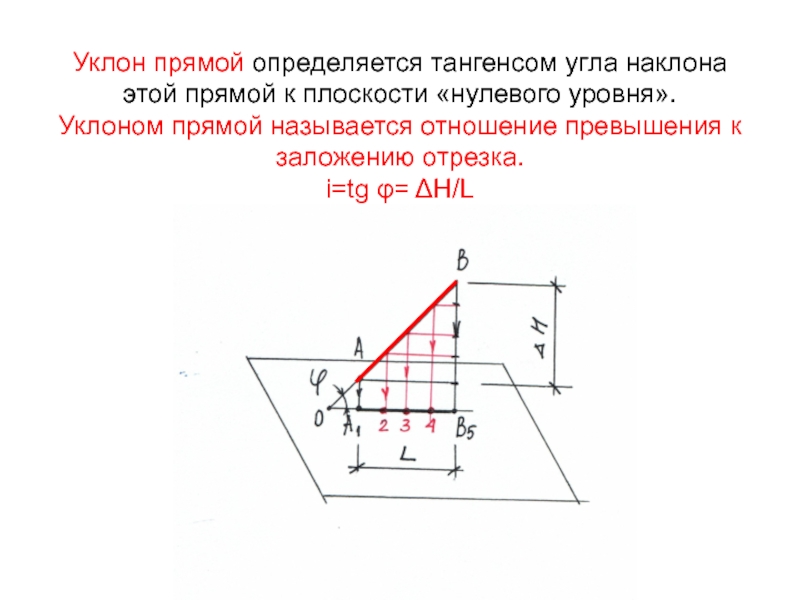
Слайд 8Уклон прямой определяется тангенсом угла наклона этой прямой к плоскости
«нулевого уровня».
Уклоном прямой называется отношение превышения к заложению отрезка.
i=tg φ=
ΔH/L
Слайд 9Величина, обратная уклону прямой называется интервалом прямой. L =Ctg φ=1/i
Интервал прямой- заложение единичного отрезка этой прямой (L).
(Единичный отрезок-
отрезок прямой, у которого разница между отметками концов =1м)
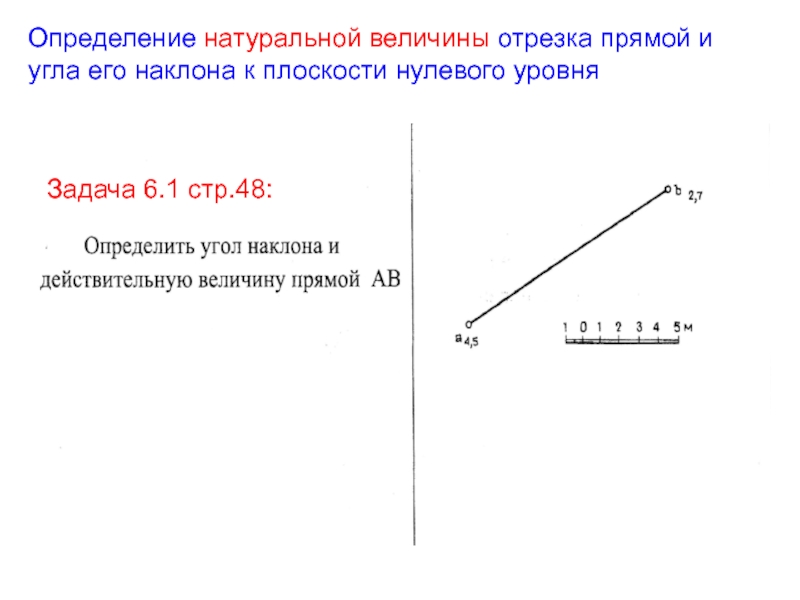
Слайд 10Задача 6.1 стр.48:
Определение натуральной величины отрезка прямой и
угла его наклона
к плоскости нулевого уровня
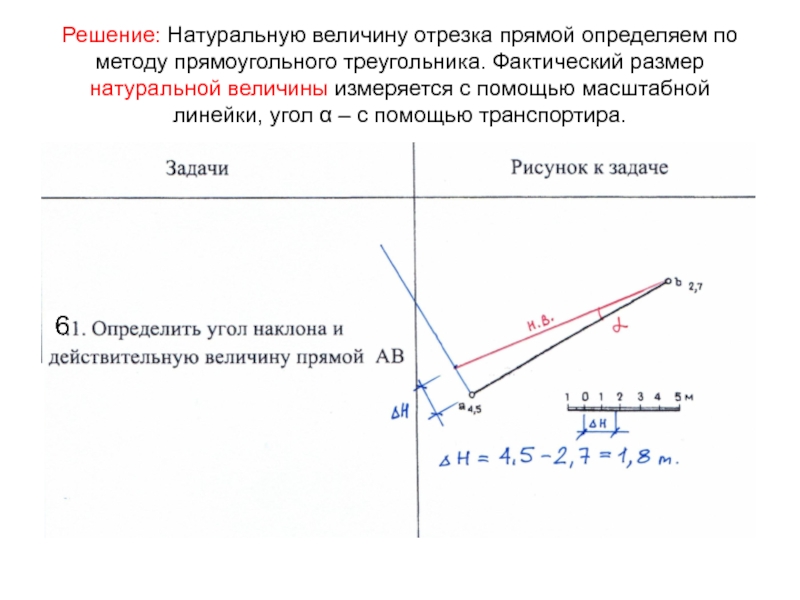
Слайд 11Решение: Натуральную величину отрезка прямой определяем по методу прямоугольного треугольника.
Фактический размер натуральной величины измеряется с помощью масштабной линейки, угол
α – с помощью транспортира.
6
Слайд 12Градуирование прямой
Прямая может быть задана точками, имеющими дробные числовые отметки,
а для решения целого ряда задач удобно иметь отметки точек
прямой, выраженные целыми числами.
Отыскание на проекции заданного отрезка точек, отметки которых равны целым числам и отличаются на единицу от отметок рассматриваемых соседних точек, называется градуированием прямой.
Слайд 13Градуирование прямой
задача: градуировать отрезок прямой А(25) В(20,3).
0 1
2м
Слайд 14
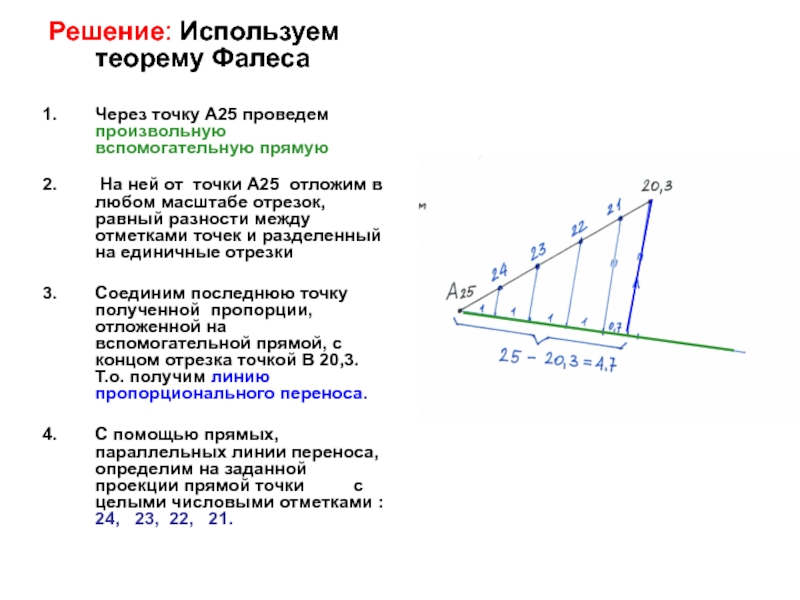
Решение: Используем теорему Фалеса
Через точку А25 проведем произвольную вспомогательную
прямую
На ней от точки А25 отложим в любом масштабе
отрезок, равный разности между отметками точек и разделенный на единичные отрезки
Соединим последнюю точку полученной пропорции, отложенной на вспомогательной прямой, с концом отрезка точкой В 20,3. Т.о. получим линию пропорционального переноса.
С помощью прямых, параллельных линии переноса, определим на заданной проекции прямой точки с целыми числовыми отметками : 24, 23, 22, 21.
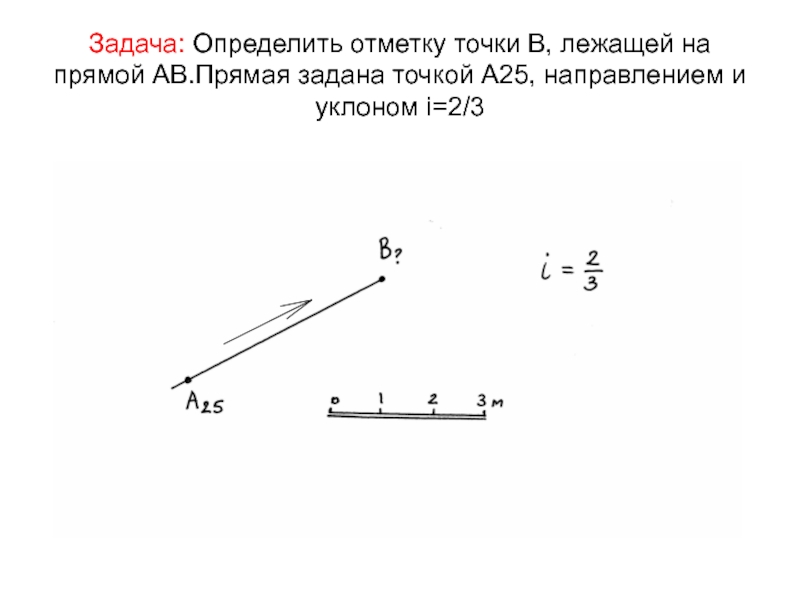
Слайд 15Задача: Определить отметку точки В, лежащей на прямой АВ.Прямая задана
точкой А25, направлением и уклоном i=2/3
Слайд 16Решение:
1.Определяем величину интервала прямой
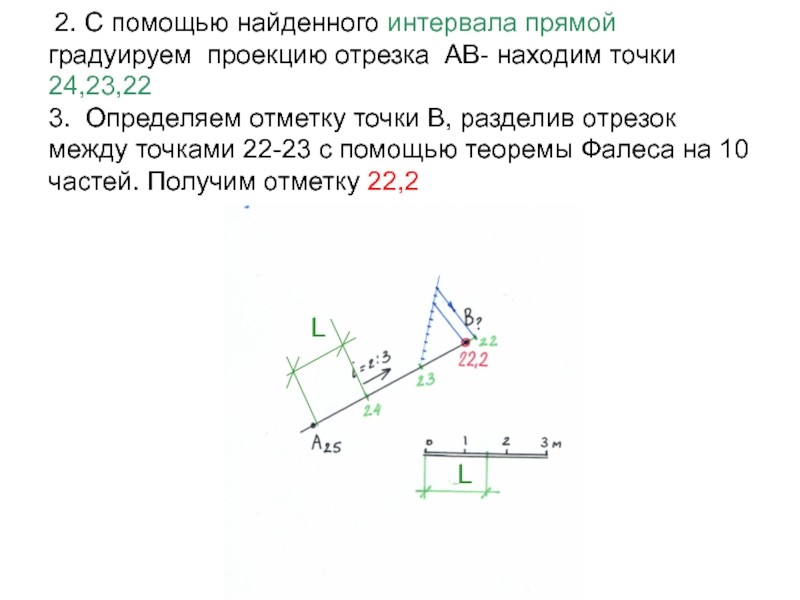
Слайд 17 2. С помощью найденного интервала прямой градуируем проекцию отрезка
АВ- находим точки 24,23,22
3. Определяем отметку точки В, разделив отрезок
между точками 22-23 с помощью теоремы Фалеса на 10 частей. Получим отметку 22,2
L
L
Слайд 18Взаимное положение прямых
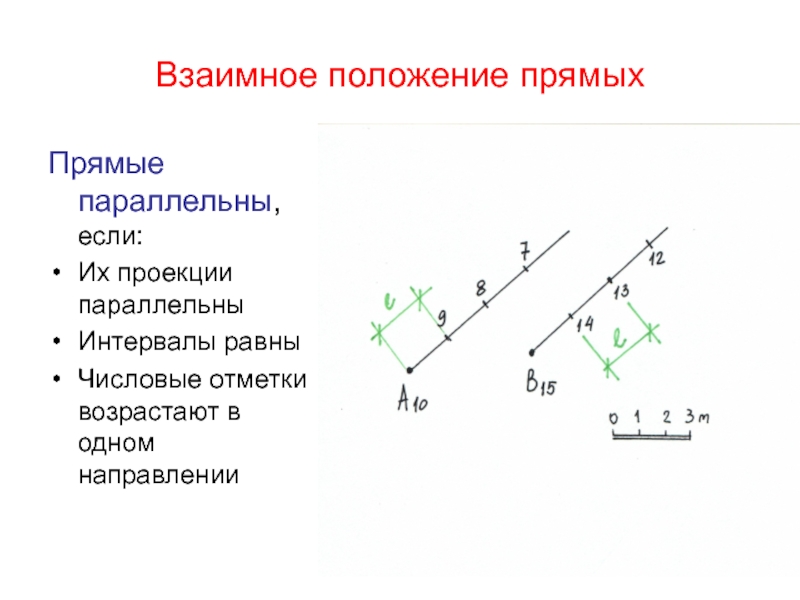
Прямые параллельны, если:
Их проекции параллельны
Интервалы равны
Числовые отметки возрастают
в одном направлении
Слайд 19Взаимное положение прямых
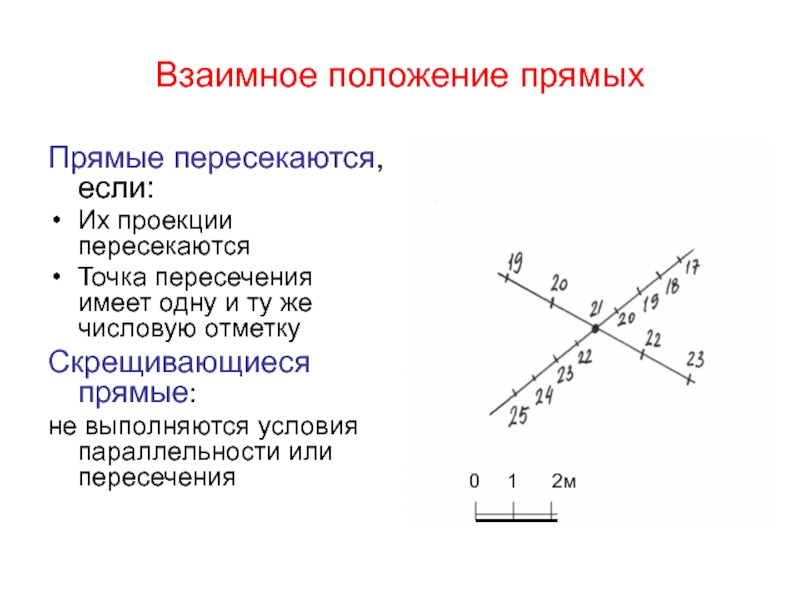
Прямые пересекаются, если:
Их проекции пересекаются
Точка пересечения имеет одну
и ту же числовую отметку
Скрещивающиеся прямые:
не выполняются условия параллельности
или пересечения
0 1 2м
Слайд 20Рассмотрим пример:
Через точку С провести прямую, параллельную данной АВ
0
1 2м
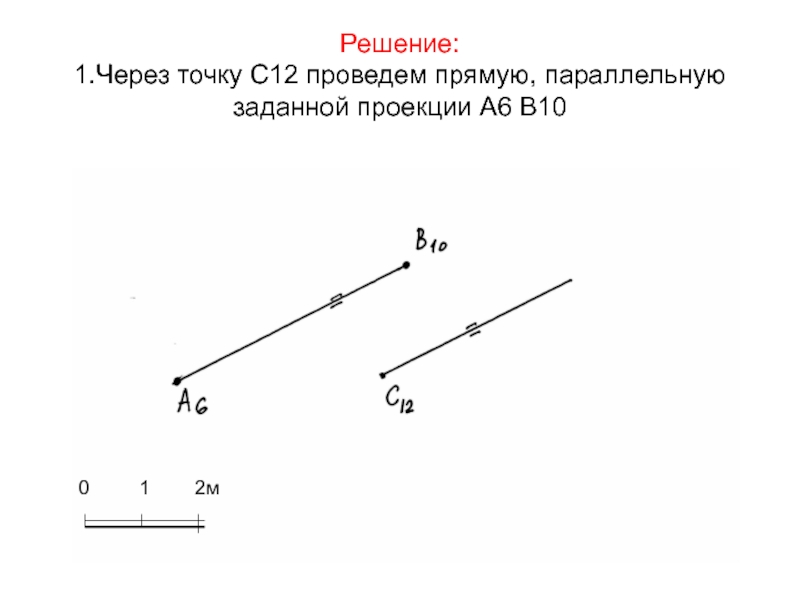
Слайд 21Решение:
1.Через точку С12 проведем прямую, параллельную заданной проекции А6
В10
0 1 2м
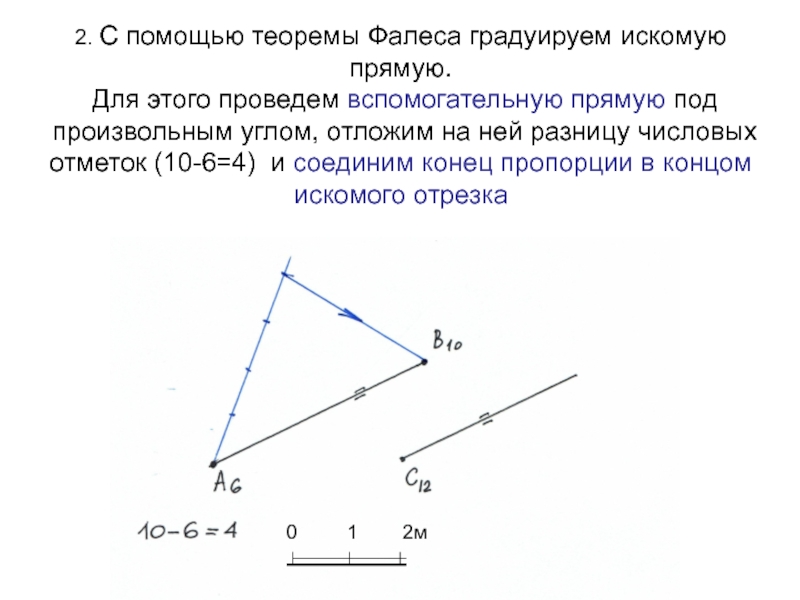
Слайд 222. С помощью теоремы Фалеса градуируем искомую прямую.
Для
этого проведем вспомогательную прямую под произвольным углом, отложим на ней
разницу числовых отметок (10-6=4) и соединим конец пропорции в концом искомого отрезка
0 1 2м
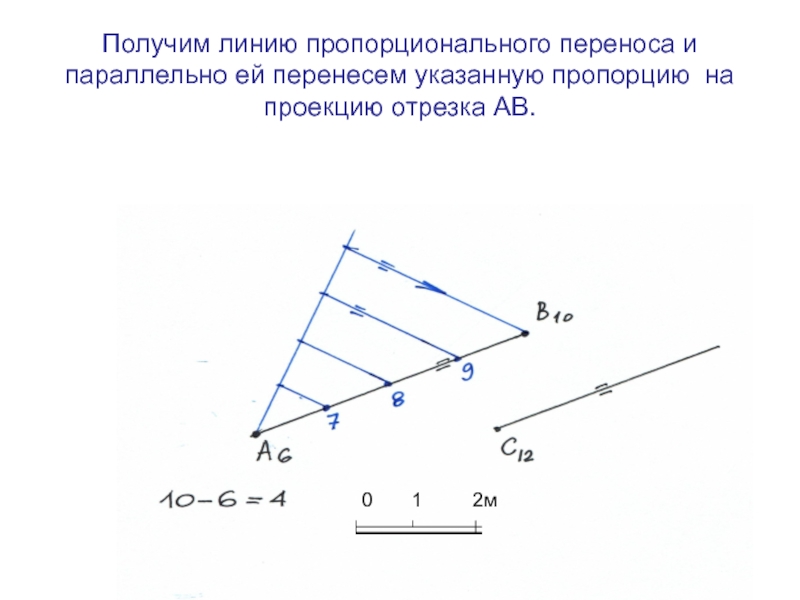
Слайд 23Получим линию пропорционального переноса и параллельно ей перенесем указанную пропорцию
на проекцию отрезка АВ.
0 1
2м
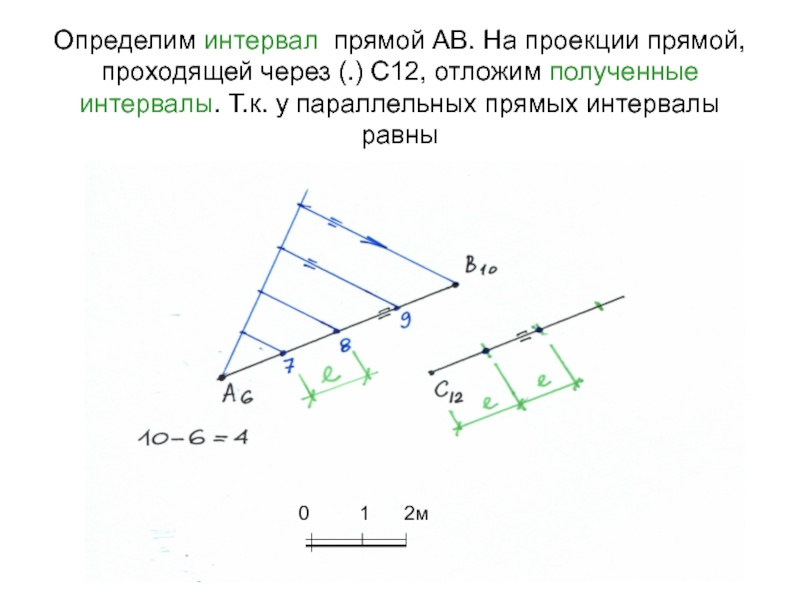
Слайд 24Определим интервал прямой АВ. На проекции прямой, проходящей через (.)
С12, отложим полученные интервалы. Т.к. у параллельных прямых интервалы равны
0
1 2м
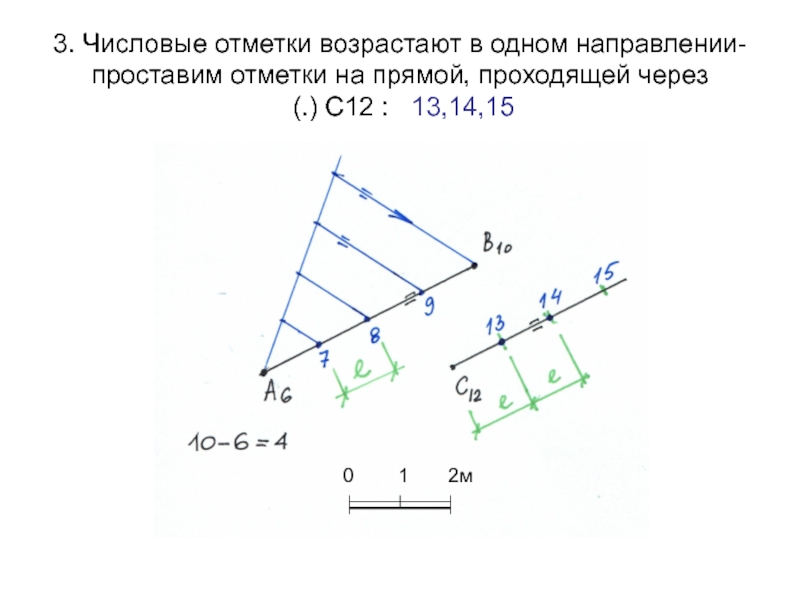
Слайд 253. Числовые отметки возрастают в одном направлении- проставим отметки на
прямой, проходящей через
(.) С12 : 13,14,15
0
1 2м
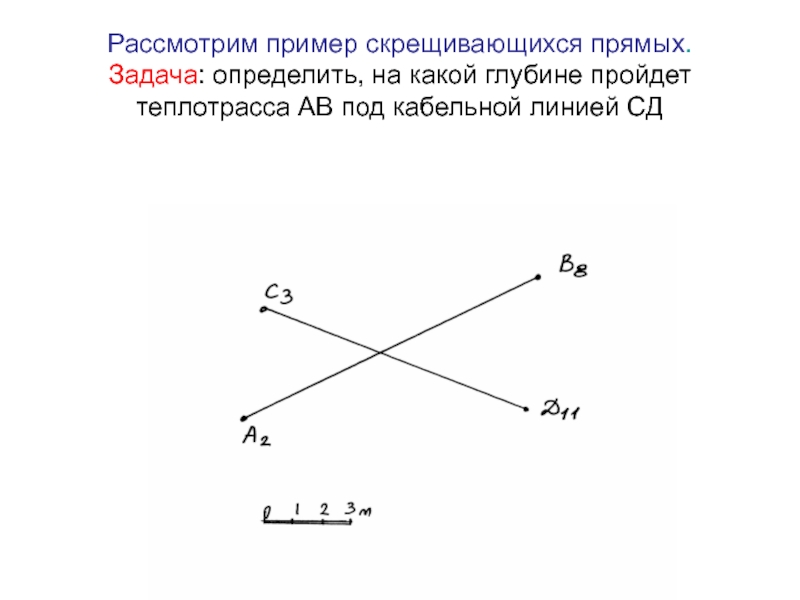
Слайд 26Рассмотрим пример скрещивающихся прямых.
Задача: определить, на какой глубине пройдет
теплотрасса АВ под кабельной линией СД
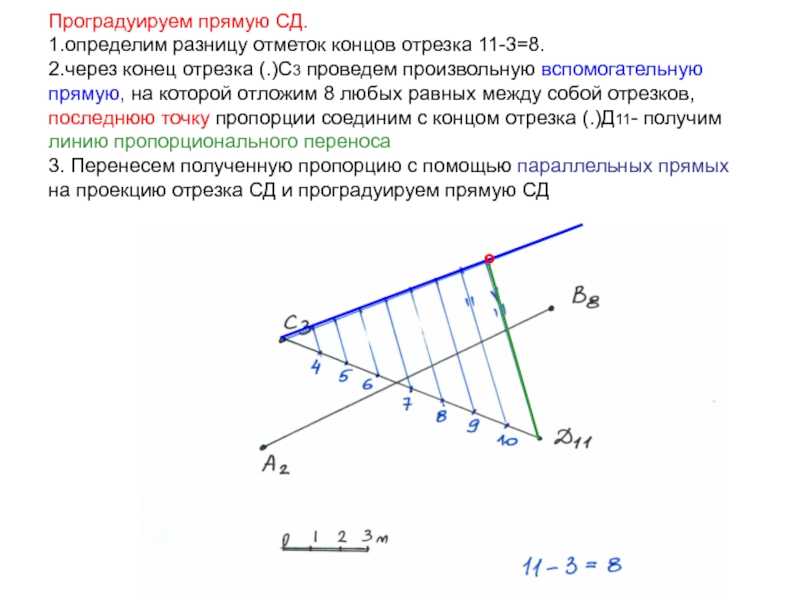
Слайд 27Проградуируем прямую СД.
1.определим разницу отметок концов отрезка 11-3=8.
2.через конец отрезка
(.)С3 проведем произвольную вспомогательную прямую, на которой отложим 8 любых
равных между собой отрезков, последнюю точку пропорции соединим с концом отрезка (.)Д11- получим линию пропорционального переноса
3. Перенесем полученную пропорцию с помощью параллельных прямых на проекцию отрезка СД и проградуируем прямую СД
°
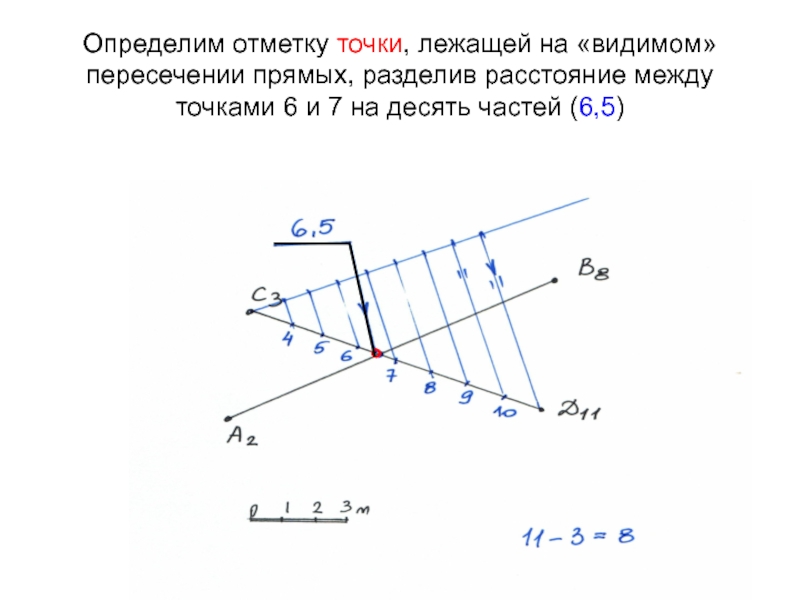
Слайд 28Определим отметку точки, лежащей на «видимом» пересечении прямых, разделив расстояние
между точками 6 и 7 на десять частей (6,5)
°
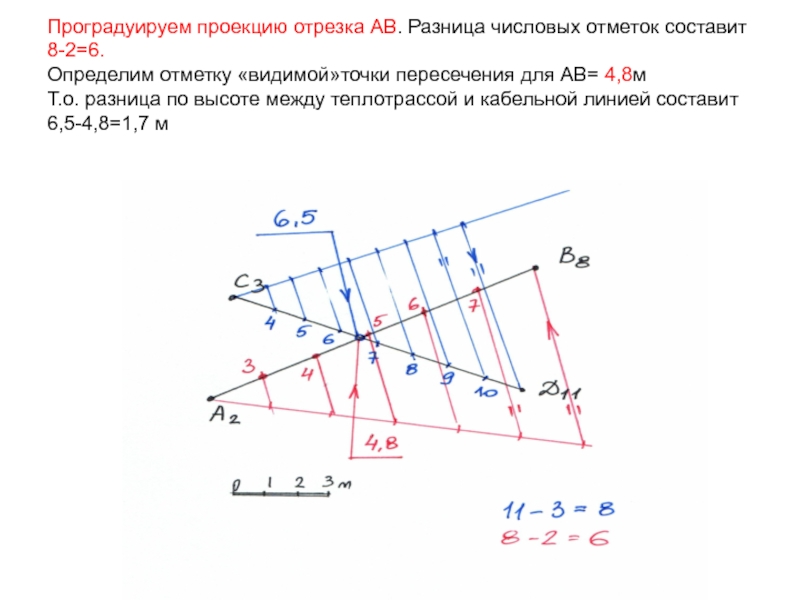
Слайд 29Проградуируем проекцию отрезка АВ. Разница числовых отметок составит 8-2=6.
Определим отметку
«видимой»точки пересечения для АВ= 4,8м
Т.о. разница по высоте между теплотрассой
и кабельной линией составит 6,5-4,8=1,7 м
Слайд 30Проекции плоскостей
Плоскость в проекциях с числовыми отметками может быть задана:
Тремя
точками с числовыми отметками
Точкой и прямой
Двумя параллельными прямыми
Двумя пересекающимися прямыми
Отсеком
(фрагмент плоскости)
Масштабом уклона плоскости
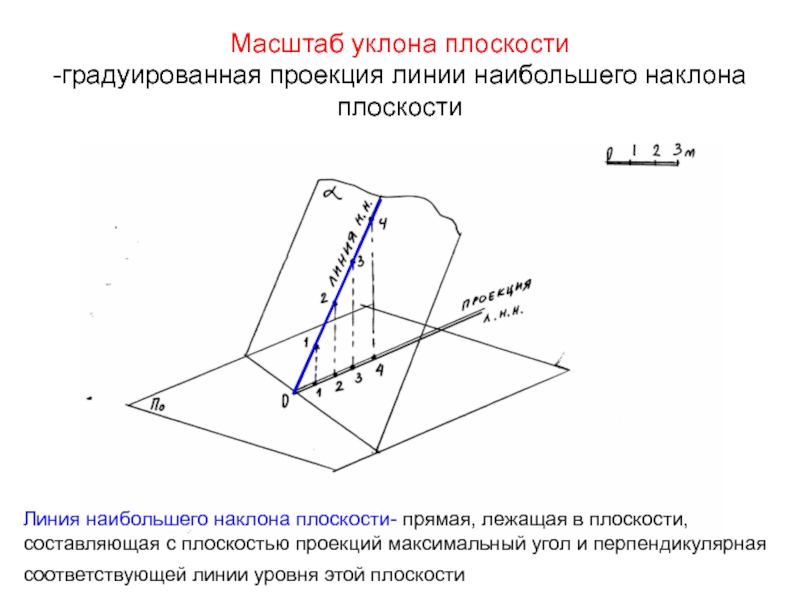
Слайд 31Масштаб уклона плоскости
-градуированная проекция линии наибольшего наклона плоскости
Линия наибольшего наклона
плоскости- прямая, лежащая в плоскости,
составляющая с плоскостью проекций максимальный
угол и перпендикулярная соответствующей линии уровня этой плоскости
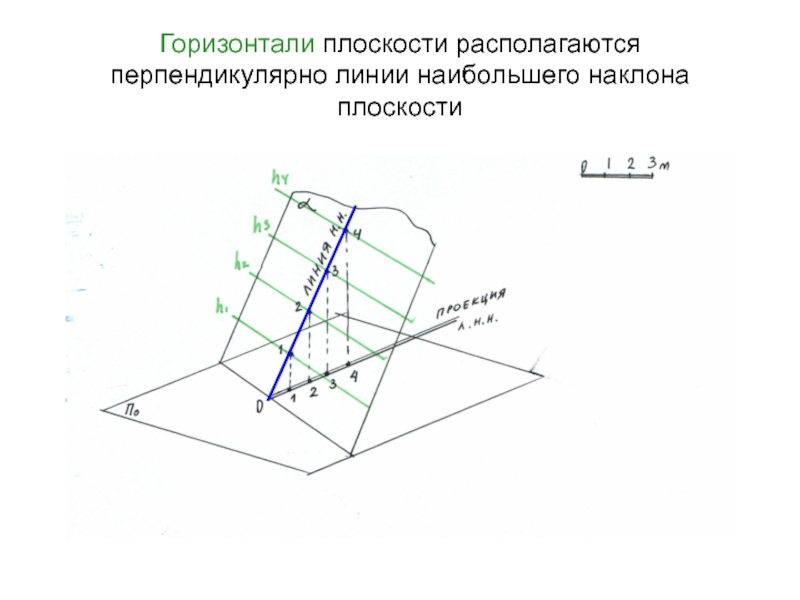
Слайд 32Горизонтали плоскости располагаются перпендикулярно линии наибольшего наклона плоскости
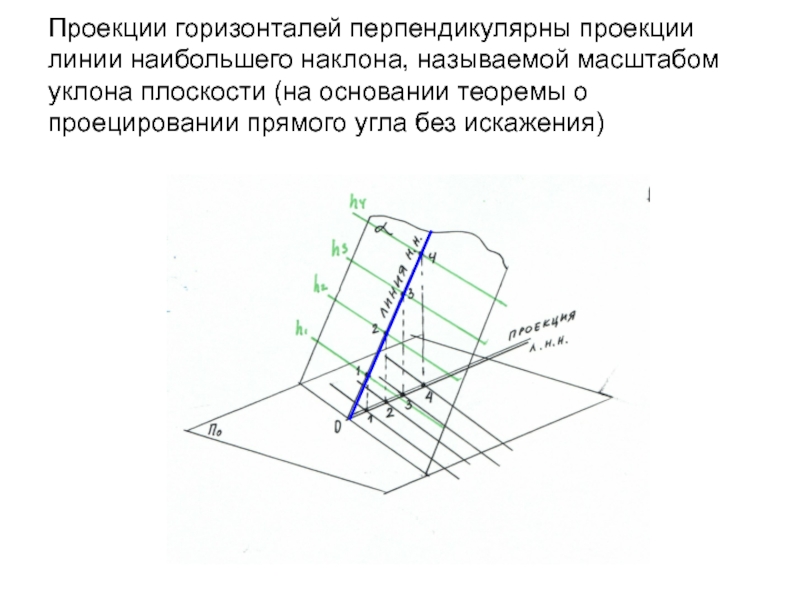
Слайд 33Проекции горизонталей перпендикулярны проекции линии наибольшего наклона, называемой масштабом уклона
плоскости (на основании теоремы о проецировании прямого угла без искажения)
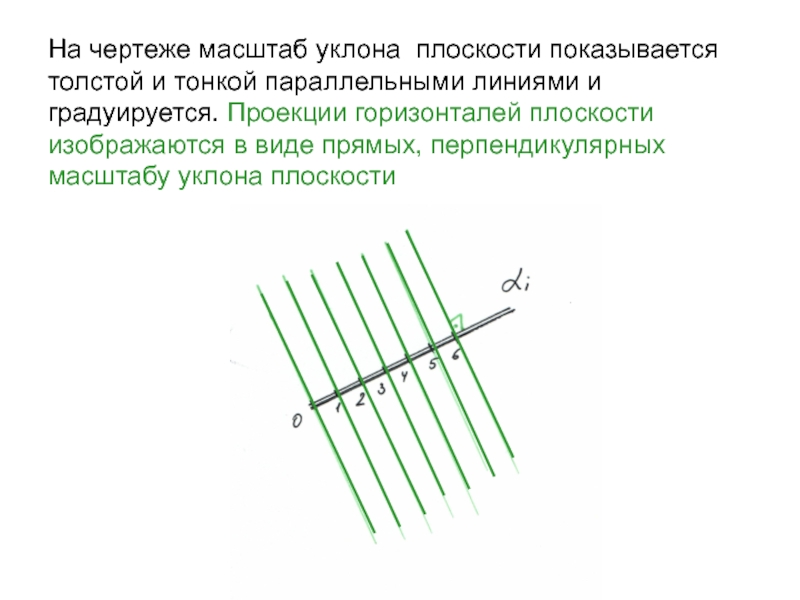
Слайд 34На чертеже масштаб уклона плоскости показывается толстой и тонкой параллельными
линиями и градуируется. Проекции горизонталей плоскости изображаются в виде прямых,
перпендикулярных масштабу уклона плоскости
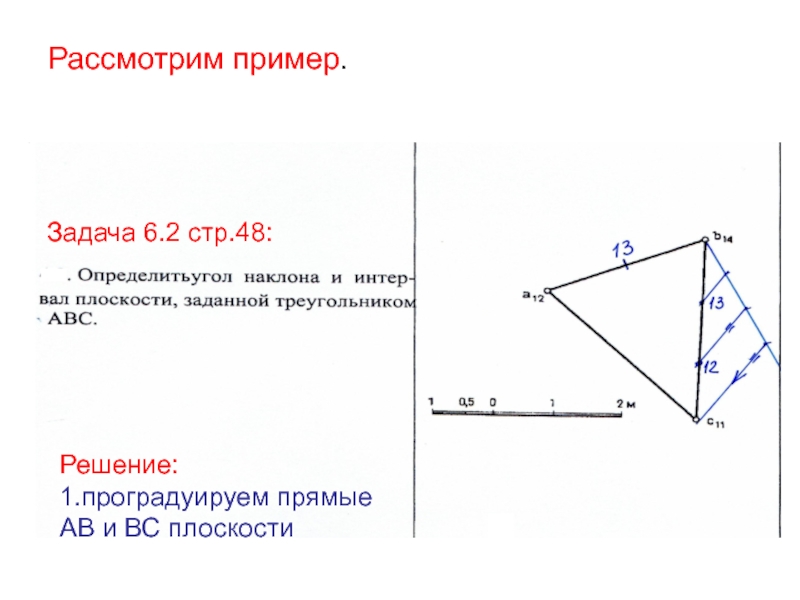
Слайд 35Рассмотрим пример.
Задача 6.2 стр.48:
Решение:
1.проградуируем прямые АВ и ВС плоскости
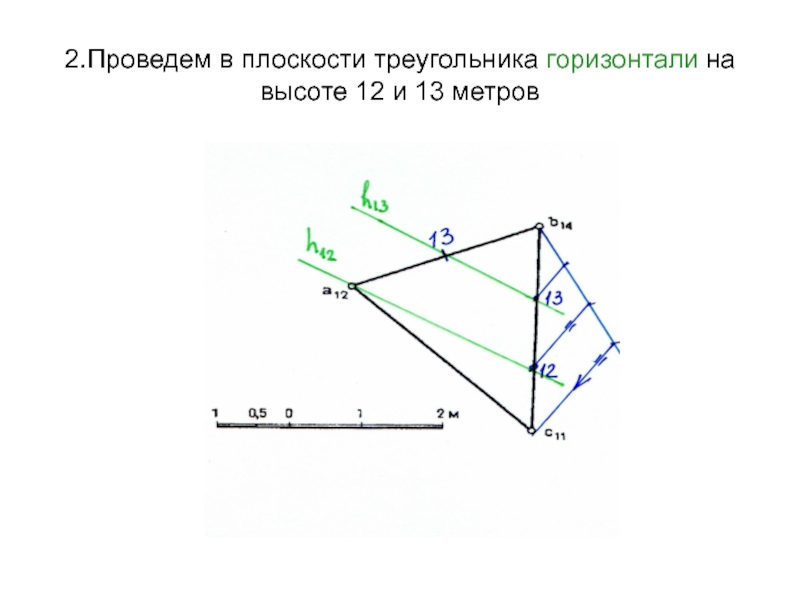
Слайд 362.Проведем в плоскости треугольника горизонтали на высоте 12 и 13
метров
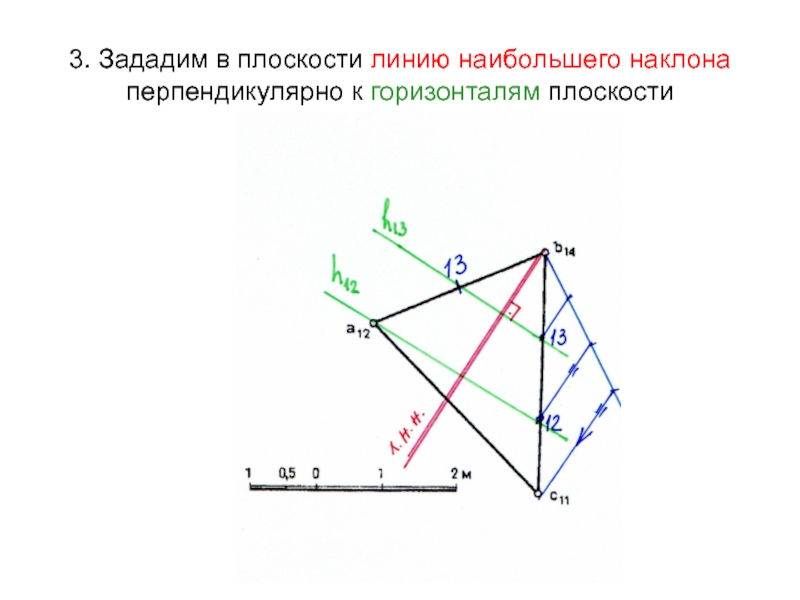
Слайд 373. Зададим в плоскости линию наибольшего наклона перпендикулярно к горизонталям
плоскости
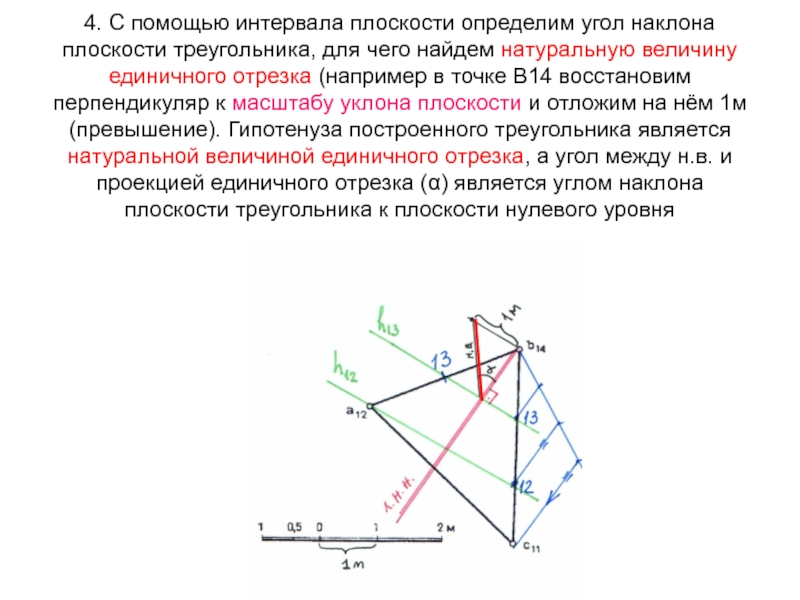
Слайд 384. С помощью интервала плоскости определим угол наклона плоскости треугольника,
для чего найдем натуральную величину единичного отрезка (например в точке
В14 восстановим перпендикуляр к масштабу уклона плоскости и отложим на нём 1м (превышение). Гипотенуза построенного треугольника является натуральной величиной единичного отрезка, а угол между н.в. и проекцией единичного отрезка (α) является углом наклона плоскости треугольника к плоскости нулевого уровня
Слайд 39Взаимное расположение точки , прямой и плоскости
Точка принадлежит плоскости, если
она принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если
она:
проходит через две точки плоскости
проходит через точку плоскости, параллельно прямой, лежащей в этой плоскости
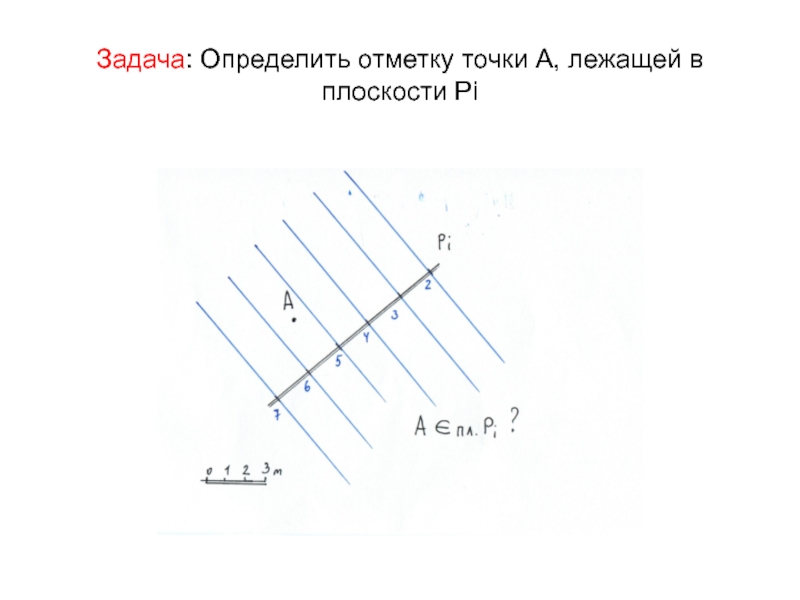
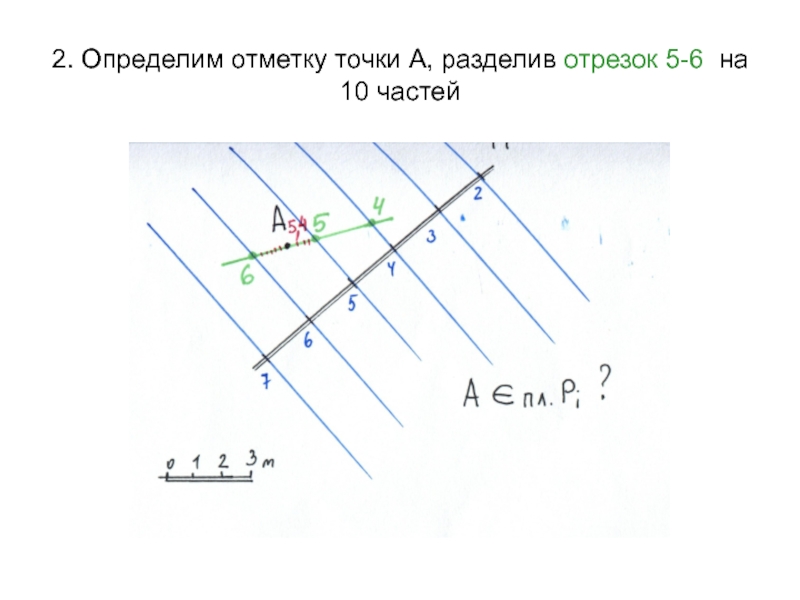
Слайд 40Задача: Определить отметку точки А, лежащей в плоскости Рi
Слайд 41Решение:
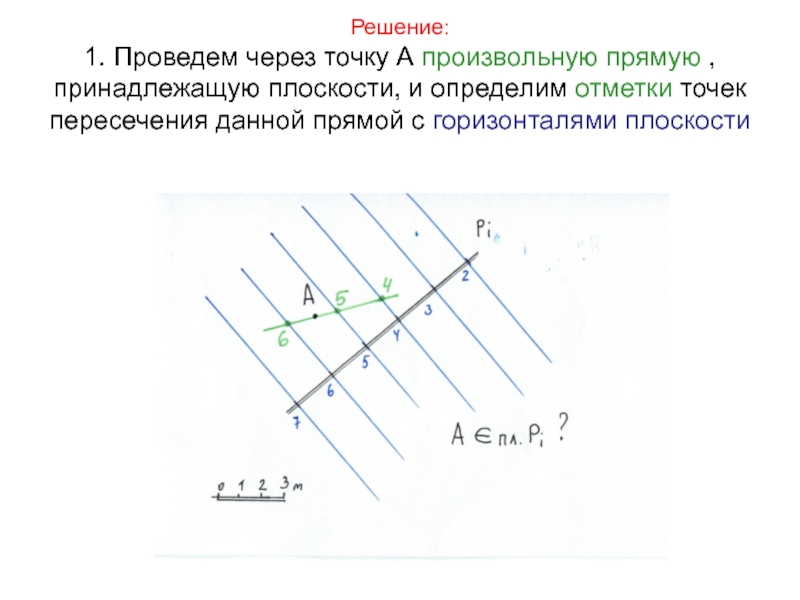
1. Проведем через точку А произвольную прямую , принадлежащую плоскости,
и определим отметки точек пересечения данной прямой с горизонталями плоскости
Слайд 422. Определим отметку точки А, разделив отрезок 5-6 на 10
частей
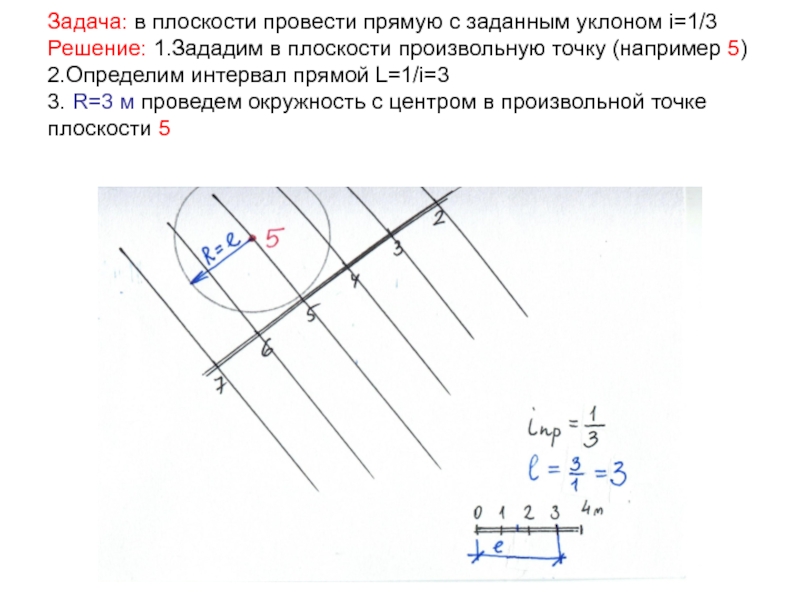
Слайд 43Задача: в плоскости провести прямую с заданным уклоном i=1/3
Решение: 1.Зададим
в плоскости произвольную точку (например 5)
2.Определим интервал прямой L=1/i=3
3. R=3
м проведем окружность с центром в произвольной точке плоскости 5
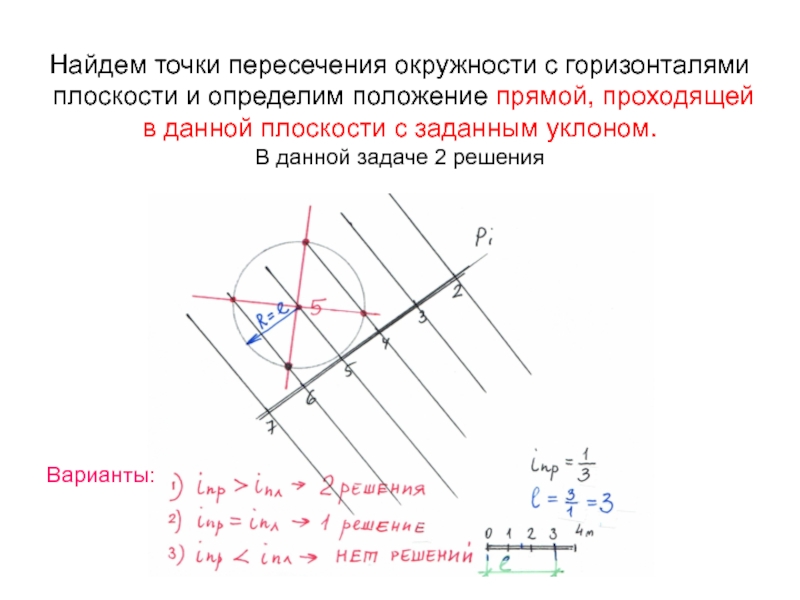
Слайд 44Найдем точки пересечения окружности с горизонталями плоскости и определим положение
прямой, проходящей в данной плоскости с заданным уклоном.
В данной задаче
2 решения
Варианты:
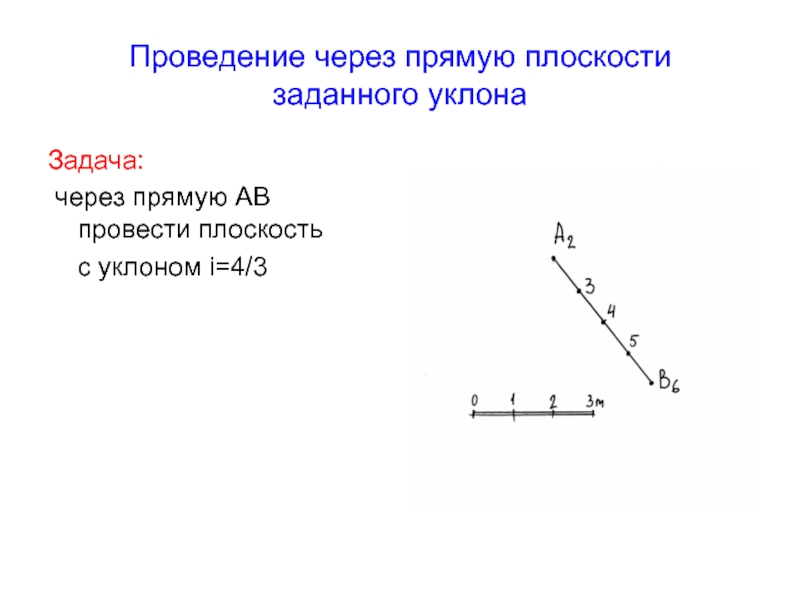
Слайд 45Проведение через прямую плоскости
заданного уклона
Задача:
через
прямую АВ провести плоскость
с уклоном i=4/3
Слайд 46Проведение через прямую плоскости
заданного уклона
Решение:
1. Определим интервал плоскости
L=1/i=3/4.
Для нахождения графической величины интервала зададим сетку
с шагом 1 м. Построим прямую с уклоном 4:3 и определим заложение единичного отрезка (превышение которого составляет 1 м)
Слайд 47Проведение через прямую плоскости
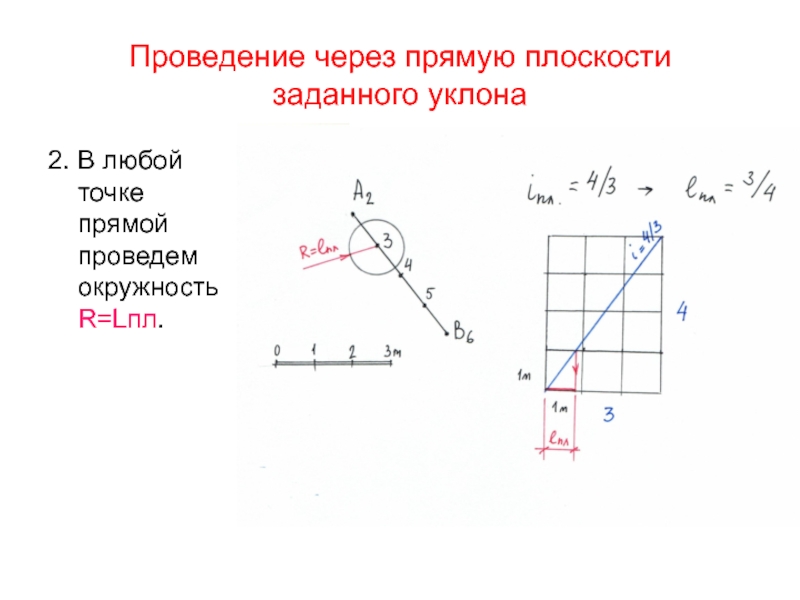
заданного уклона
2. В любой точке прямой
проведем окружность R=Lпл.
Слайд 48Проведение через прямую плоскости
заданного уклона
3.Проведем касательные к полученной окружности
- горизонтали проектной плоскости.
Возможны варианты:
Интервал плоскости меньше интервала прямой =
2 решения
Интервал плоскости равен интервалу прямой = 1 решение
Интервал плоскости больше интервала прямой = нет решений
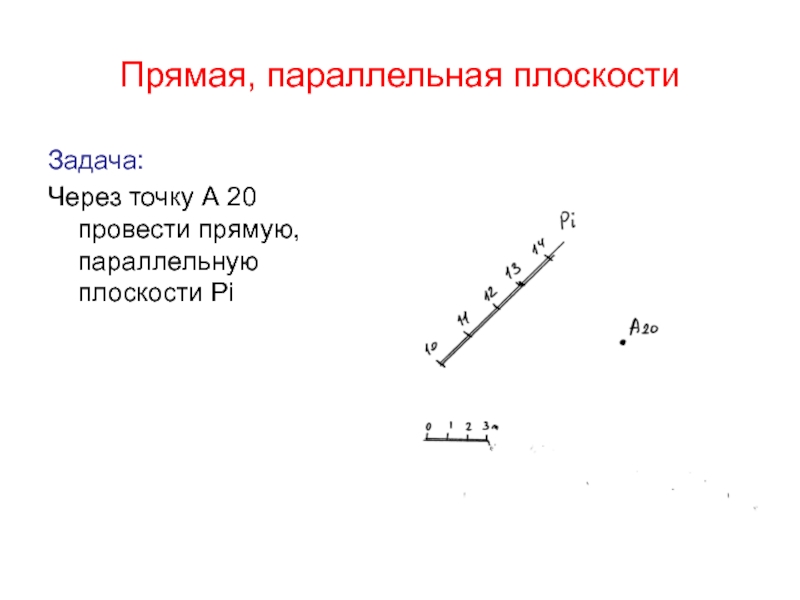
Слайд 49Прямая, параллельная плоскости
Задача:
Через точку А 20 провести прямую, параллельную плоскости
Рi
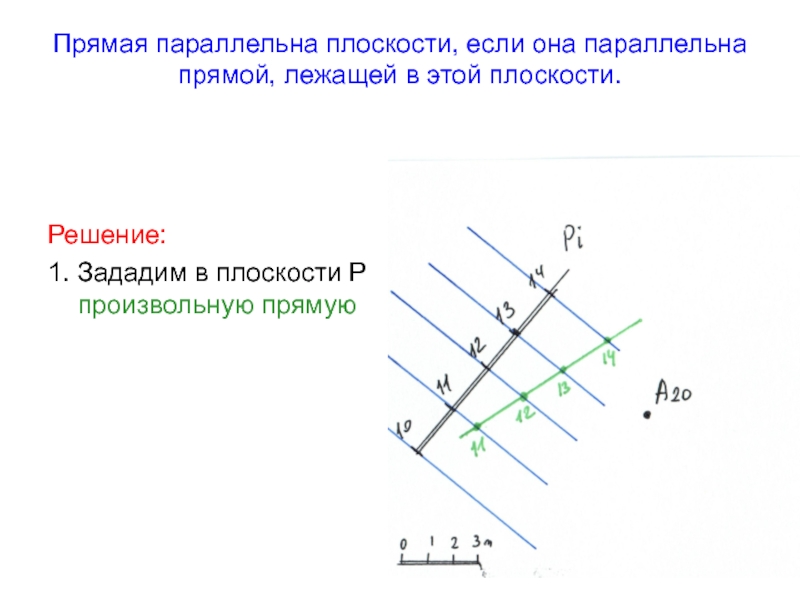
Слайд 50Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой
плоскости.
Решение:
1. Зададим в плоскости Р произвольную прямую
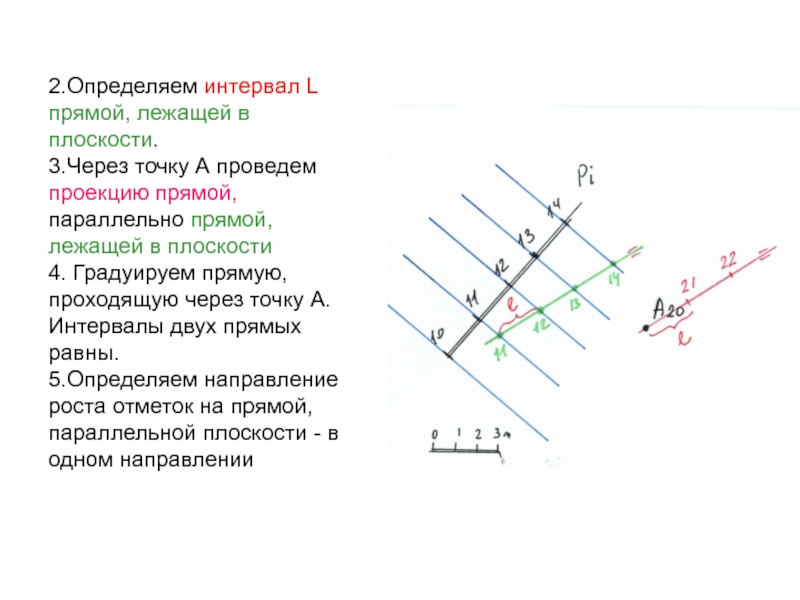
Слайд 512.Определяем интервал L прямой, лежащей в плоскости.
3.Через точку А проведем
проекцию прямой, параллельно прямой, лежащей в плоскости
4. Градуируем прямую, проходящую
через точку А. Интервалы двух прямых равны.
5.Определяем направление роста отметок на прямой, параллельной плоскости - в одном направлении
Слайд 52Пересечение прямой с плоскостью
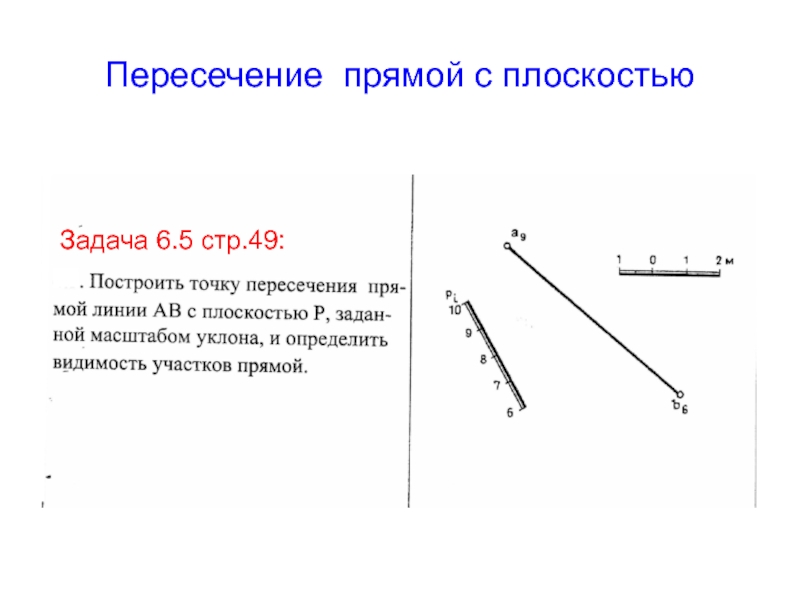
Задача 6.5 стр.49:
Слайд 53Решение:
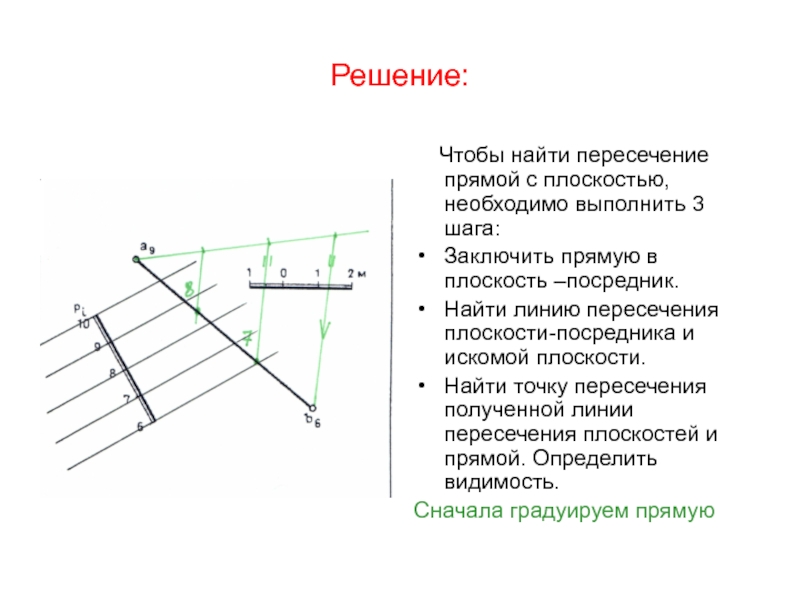
Чтобы найти пересечение прямой с плоскостью, необходимо выполнить
3 шага:
Заключить прямую в плоскость –посредник.
Найти линию пересечения плоскости-посредника и
искомой плоскости.
Найти точку пересечения полученной линии пересечения плоскостей и прямой. Определить видимость.
Сначала градуируем прямую
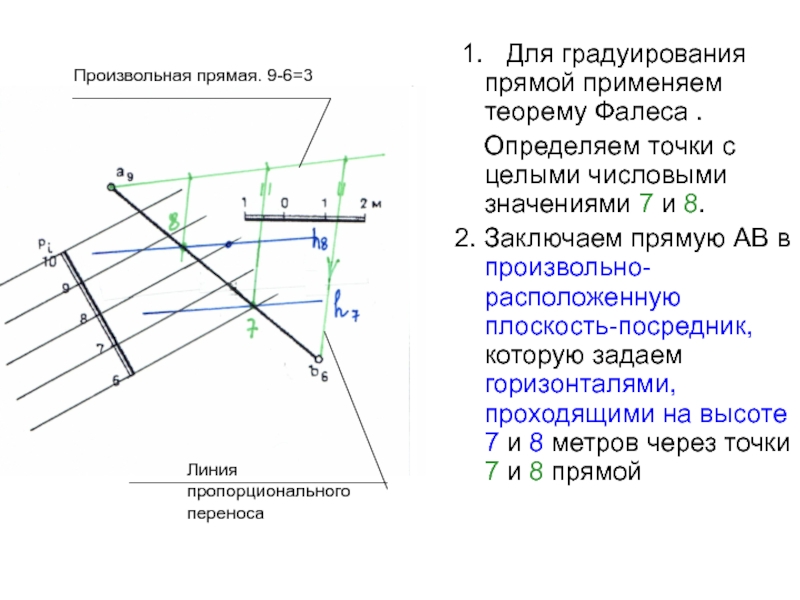
Слайд 54 1. Для градуирования прямой применяем теорему Фалеса .
Определяем точки с целыми числовыми значениями 7 и 8.
2.
Заключаем прямую АВ в произвольно-расположенную плоскость-посредник, которую задаем горизонталями, проходящими на высоте 7 и 8 метров через точки 7 и 8 прямой
Произвольная прямая. 9-6=3
Линия пропорционального
переноса
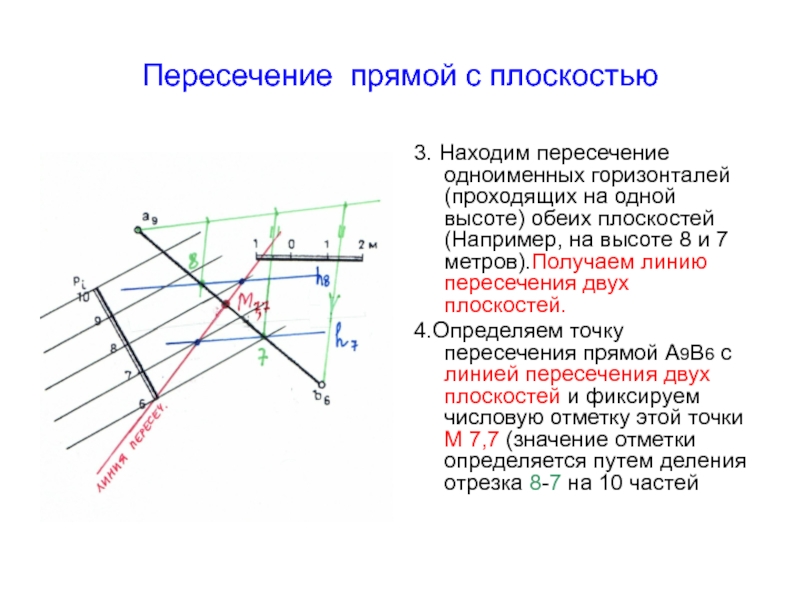
Слайд 55Пересечение прямой с плоскостью
3. Находим пересечение одноименных горизонталей (проходящих на
одной высоте) обеих плоскостей (Например, на высоте 8 и 7
метров).Получаем линию пересечения двух плоскостей.
4.Определяем точку пересечения прямой А9В6 с линией пересечения двух плоскостей и фиксируем числовую отметку этой точки М 7,7 (значение отметки определяется путем деления отрезка 8-7 на 10 частей
Слайд 56Взаимное расположение плоскостей
Две плоскости в пространстве могут быть взаимно параллельными
или пересекающимися.
Параллельные между собой плоскости имеют взаимно параллельные масштабы уклона,
с равными интервалами и возрастанием (или убыванием) отметок в одном направлении.
Если масштабы уклона заданных плоскостей не удовлетворяют хотя бы одному условию взаимной параллельности , то такие плоскости пересекаются
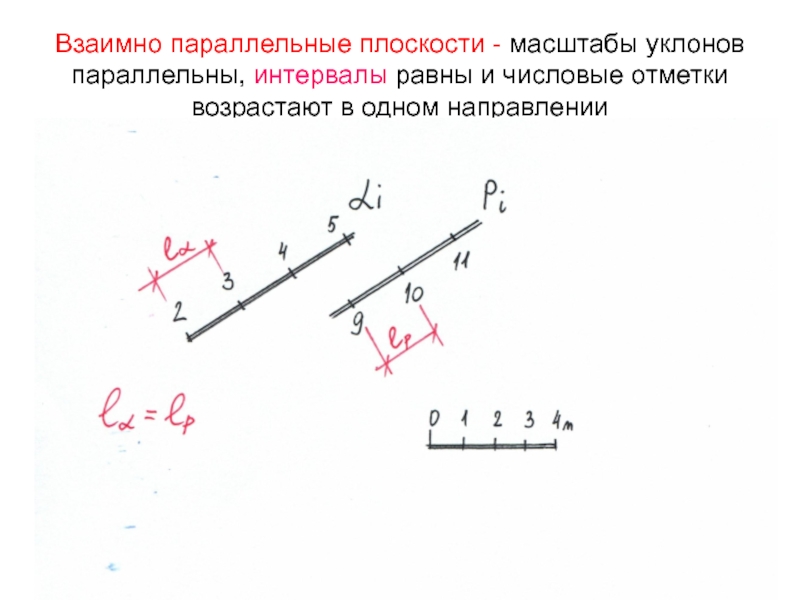
Слайд 57Взаимно параллельные плоскости - масштабы уклонов параллельны, интервалы равны и
числовые отметки возрастают в одном направлении
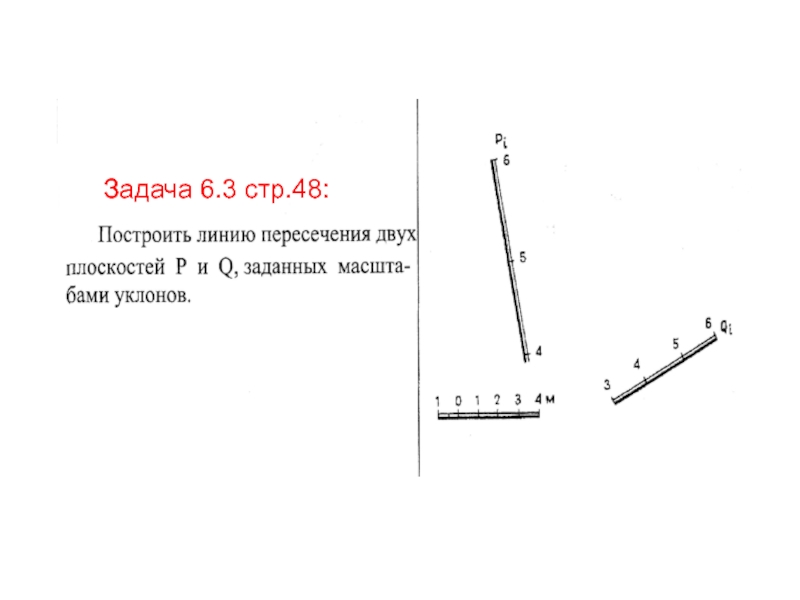
Слайд 59Пересекающиеся плоскости
. Для нахождения линии пересечения 2-х плоскостей надо найти
точки пересечения одноименных горизонталей
Задача 6.3 стр.48:
Слайд 60Поверхности
В проекциях с числовыми отметками поверхности задаются своими горизонталями, получаемыми
от мысленного пересечения их горизонтальными плоскостями, проводимыми на расстоянии единицы
масштаба (обычно 1 м) друг от друга.
Если поверхность закономерная, ее горизонтали имеют известную форму и расположены в определенном порядке.
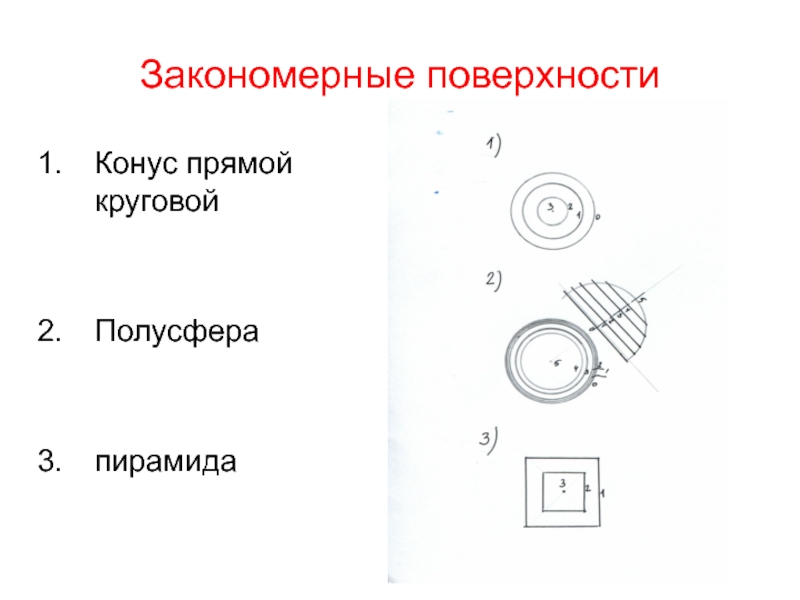
Слайд 61Закономерные поверхности
Конус прямой круговой
Полусфера
пирамида
Слайд 62Графические поверхности
Незакономерные поверхности называют графическими.
Земная поверхность является графической и называется
топографическая поверхность.
По горизонталям такой поверхности можно судить о рельефе
местности. Расстояния между горизонталями определяют уклон топографической поверхности в том или ином направлении. Если расстояние между горизонталями уменьшается, значит уклон данной поверхности становится круче(больше) и наоборот.
Например: а) холм, б) овраг
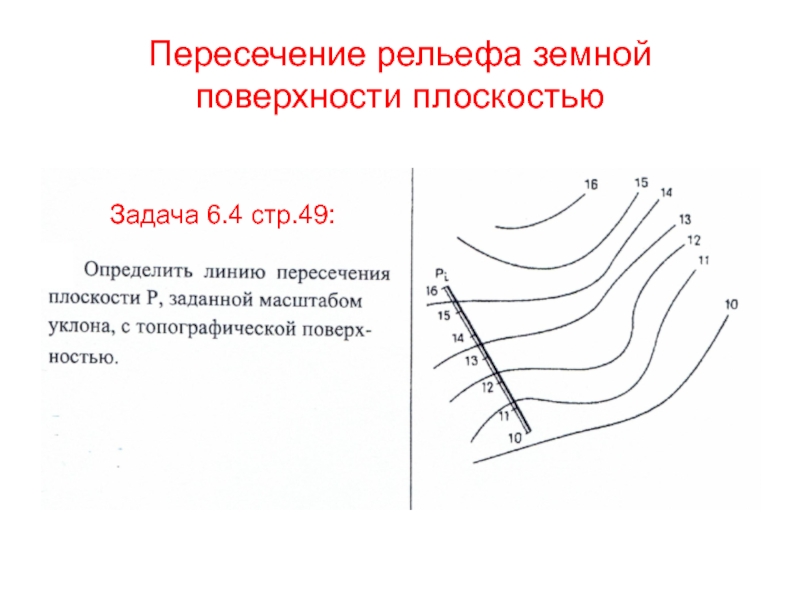
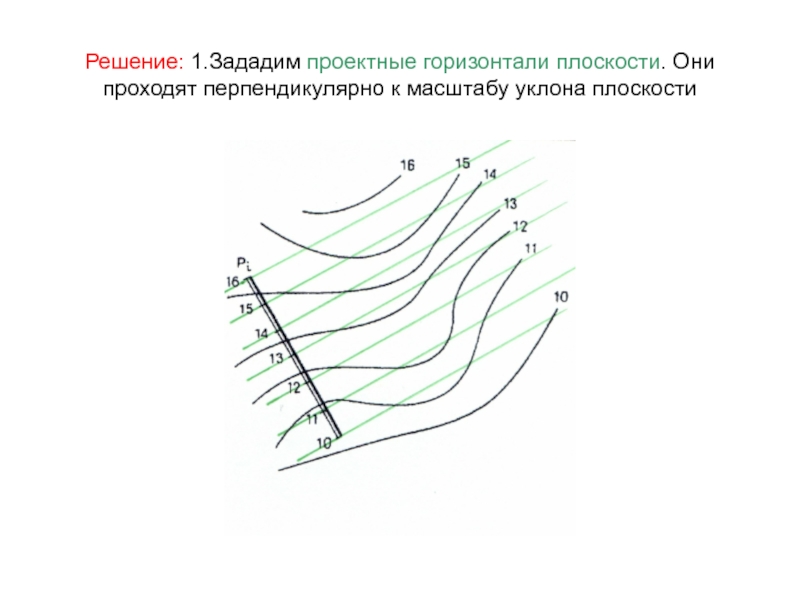
Слайд 63Пересечение рельефа земной поверхности плоскостью
Задача 6.4 стр.49:
Слайд 64Решение: 1.Зададим проектные горизонтали плоскости. Они проходят перпендикулярно к масштабу
уклона плоскости
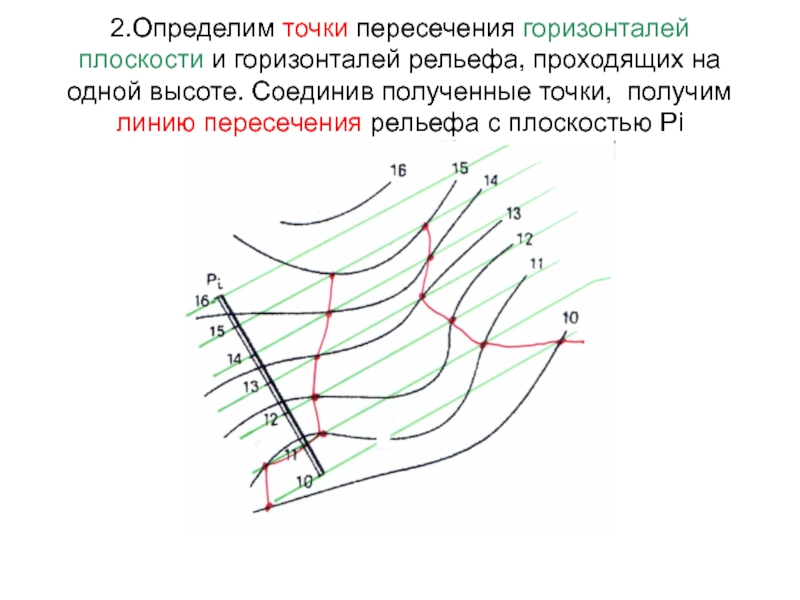
Слайд 652.Определим точки пересечения горизонталей плоскости и горизонталей рельефа, проходящих на
одной высоте. Соединив полученные точки, получим линию пересечения рельефа с
плоскостью Рi
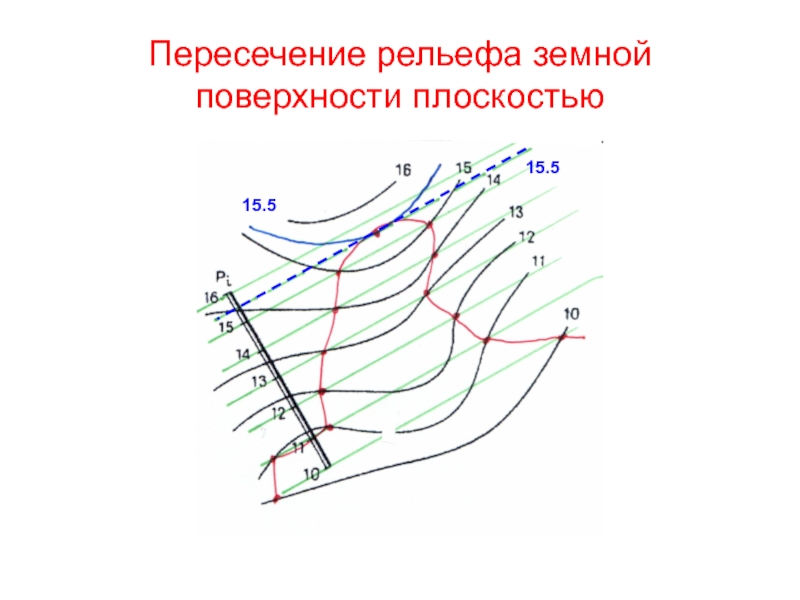
Слайд 66Т.к. горизонтали на высоте 16 м не пересеклись, задаем промежуточные
проектные и рельефные горизонтали через 0,5 м (0,25м) и определяем
пиковую точку на пересечении
горизонталей , расположенных на высоте 15,5 м
15.5
15.5
Слайд 67Пересечение рельефа земной поверхности плоскостью
15.5
15.5