Лекция 3. Нечеткая логика. Нечеткие множества. Нечеткие алгоритмы принятия

на теории нечетких множеств, предназначенное для формализации неточных или приближенных

рассуждений, характерных для человека. /=«Математика здравого смысла»/.
1965 – понятие нечеткого множества (Fuzzy Set) – Лотфи Заде (США) = «Отец Нечеткой Логики»;
1974 – система нечеткого управления (Fuzzy Control) парогенератором – Э. Мамдани (Великобритания);
1990-е гг. – Fuzzy boom (Япония) – автомобили, фотоаппараты, видеокамеры, стиральные машины и т.д.

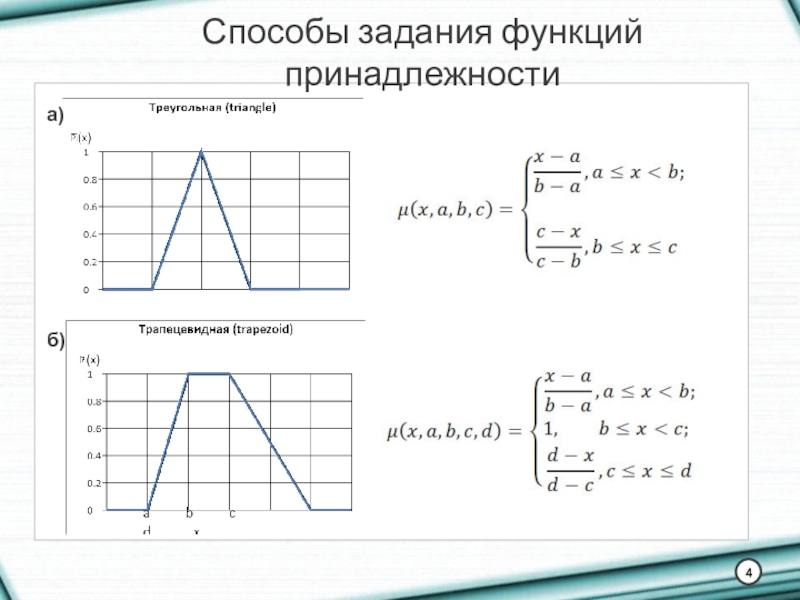
Нечеткая логика

Очень_высокая}

min {0,25; μB1 (ϕ)};
μB2 (ϕ)IT*=23°C = min {0,75;

μB2 (ϕ)};
μ (ϕ)IT*=23°C = max { μB1 (ϕ)IT*=23°C , μB2 (ϕ)IT*=23°C };
Метод дефаззификации = метод центра тяжести:


где μi и ϕi – некоторые фиксированные отсчеты функции μ(ϕ) и ϕ.

0,25* μB1 (ϕ); μB2 (ϕ)IT*=23°C = 0,75* μB2 (ϕ);
μ

(ϕ)IT*=23°C = max { μB1 (ϕ)IT*=23°C , μB2 (ϕ)IT*=23°C };
Метод дефаззификации = метод центра тяжести:


где μi и ϕi – некоторые фиксированные отсчеты функции μ(ϕ) и ϕ.

2, …, m));
Механизм логического вывода – метод MAX/MIN (или MAX/ПРОИЗВЕДЕНИЕ)

– построение функции принадлежности:
μ(y) x1=x1*
…
xm=xm*
Дефаззификация – метод центра тяжести (вычисление «четкого» значения y*)

Общая схема нечеткого алгоритма