Лекция 5

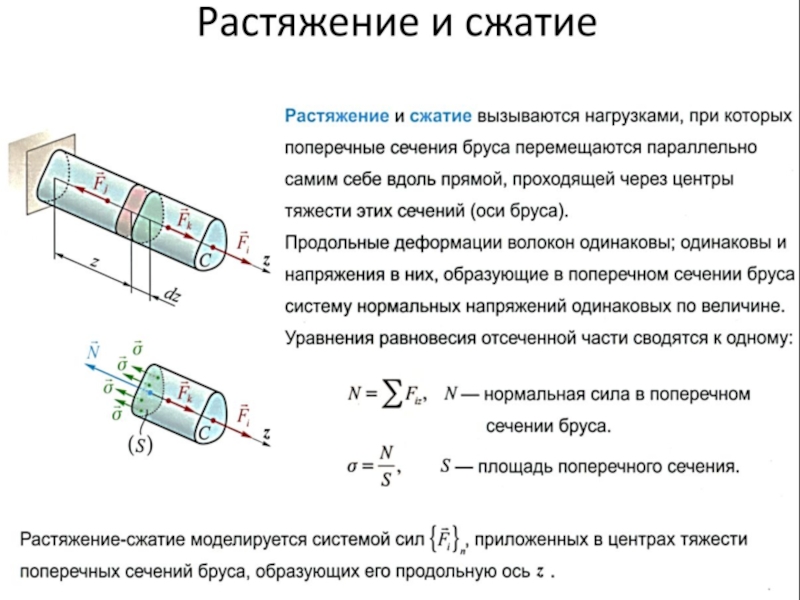
силой F. Выделим на расстоянии z участок длиной dz. Удлинение

этого участка dz равно перемещению второй его границы относительно первой dw.
Деформация на этом участке определяется выражением,
представляющим собой дифференциальное уравнение:

Разделим переменные и сведем решение этого уравнения
к интегрированию левой и правой частей:

Подставим пределы и выражение для деформации,
следующего из закона Гука:

Здесь w0 – перемещение левой границы рассматриваемого участка на расстоянии z0, EA – жесткость стержня при растяжении-сжатии,
N – продольное усилие.

В случае постоянства продольного усилия и площади поперечного сечения имеем:

Отсюда, как частный случай, получается выражение для абсолютного удлинения стержня (w0 = 0, z0 = 0, z = l):

Общая формула вычисления перемещений показывает, что перемещения исчисляются нарастающим итогом, т.е. к перемещению, вычисляемому
на рассматриваемом участке [z0 ,z] (второе слагаемое), добавляется перемещение сечения, соответствующего левой границе, и представляющего
перемещение всего участка, как жесткого целого (твердого тела). Если на каждом из участков продольное усилие и площадь поперечного сечения постоянны, то определение перемещения любого сечения или конца стержня сводится к простому суммированию удлинений каждого
из участков от неподвижного сечения до рассматриваемого.

Учет собственного веса – Рассмотрим стержень, нагруженный собственным весом (длина стержня l, объемный вес материала стержня ).

Продольное усилие от собственного веса в произвольном сечении на расстоянии z равно весу нижерасположенной части стержня
и линейно зависит от координаты. Эпюры продольной силы и нормальных напряжений имеют вид треугольников:

Перемещение произвольного сечения на расстоянии z имеет квадратичную зависимость от координаты:

Определим перемещения конца стержня и сечения на расстоянии половины длины:

Здесь G – вес стержня.

Таким образом, учет равномерно распределенной продольной нагрузки (собственный веса) может быть
выполнен непосредственным интегрированием по рассматриваемому участку или использованием
выражения, подобного абсолютному удлинению стержня при постоянной продольной силе,
в котором сила уменьшена вдвое! (см. результат определения перемещения конца стержня).

Например, второй результат (перемещение сечения посредине длины стержня) может быть получен,
как сумма перемещений рассматриваемого сечения стержня от действия собственного веса верхней
части, учитываемого как распределенная нагрузка, и перемещения его от веса нижней части,
действующего на верхнюю часть как внешняя сила:

В статически неопределимых системах число наложенных связей больше числа независимых

уравнений равновесия. Как указывалось выше, такие задачи решаются последовательным рассмотрением статической, геометрической и физической сторон, в результате чего получается полная система уравнений, позволяющая найти искомые усилия. Общий порядок решения определяется вышесказанным, конкретные шаги и особенности рассмотрим на примерах:
Пример 1. Стержень переменного сечения (2A и A) жестко заделан с двух сторон и нагружен продольной силой. Построить эпюры N и σ.

1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:

RA

RB

2. Статика : Составляем уравнение равновесия:

Это единственное уравнение равновесия, которое можно составить для линейной системы сил.
Следовательно система один раз статически неопределима.

3. Геометрия:
Составляем уравнение совместности деформаций:

Это уравнение устанавливает неизменность общей длины стержня при любых воздействиях, которую обеспечивали связи (жесткие заделки) до их удаления.

4. Физика: Записываем соотношения связи деформаций с усилиями:

Получили полную систему уравнений, решающую данную задачу (5 уравнений и 5 неизвестных – 2 реакции и 3 перемещения) .

Такой же результат можно получить с использованием статически определимой
системы, образованной из заданной статически неопределимой отбрасыванием
“лишней” связи, и принципа независимости действия сил:

RB

Подставим полученное соотношение
в уравнение равновесия:

Это уравнение устанавливает неизменность общей длины стержня, которую обеспечивала “лишняя” связь (правая жесткая заделка) до ее удаления, или равенство перемещений и их противоположное направление при отдельном действии внешней нагрузки и реакции этой связи.

или

Записываем соотношения связи деформаций
(перемещений) с усилиями:

Получили полную систему уравнений, решающую данную задачу
(4 уравнения и 4 неизвестных – 2 реакции и 2 перемещения) .

Подставляем соотношения упругости в уравнения совместности:

Составляем уравнение совместности деформаций:

Подставим полученное соотношение
в уравнение равновесия и получим
величину второй реакции (RB).

Подставляем перемещения в уравнения совместности:

Эпюра нормальных напряжений также строится
вычислением значений напряжений по участкам:
σ1 = N1 / A1= 3F/8A,
σ2 = N2 / A2= F/8A,
σ3 = N3 / A3= F/4A.
В сечении резкого изменения площади получился скачок.

Если имелся первоначальный зазор, например между правым концом
стержня и заделкой, или напротив натяг (первоначальный размер стержня
превышает расстояние между опорами), то это учитывается лишь
в уравнениях совместности деформаций:
или (>0 зазор, <0 натяг)

Если вместо силового нагружения, или дополнительно к нему, действует
температурная нагрузка (нагрев), то это учитывается введением
температурных удлинений в уравнения совместности деформаций.

14

температуры – В статически неопределимых системах нагрев (охлаждение) элементов вызывает

дополнительные внутренние усилия (напряжения), которые могут значительно превышать усилия от действия силового нагружения. Общий порядок решения задачи сохраняется, но уравнения совместности деформаций (удлинений) содержат удлинения от действия разности температур t :  -коэффициент линейного расширения материала, l – длина стержня.
Пример 2. Стержень переменного сечения (2A и A), рассмотренный в примере 1, дополнительно нагревается на t градусов.
t

1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:

RA

RB

2. Статика : Составляем уравнение равновесия:

3. Геометрия:
Составляем уравнение совместности деформаций:

Это уравнение устанавливает неизменность общей длины стержня при любых воздействиях, в том числе от нагрева, которую обеспечивали связи (жесткие заделки) до их удаления.

4. Физика: Записываем соотношения связи деформаций с усилиями и температурным
воздействием:

Подставим полученное соотношение
в уравнение равновесия:

Подставляем соотношения упругости и температурного удлинения в уравнения совместности:

Эпюру продольных сил строим вычислением значений по участкам:
N1 = RA = 4.5 кН, N2 = N3 = RB = -5.5 кН. В сечении, в котором приложена сосредоточенная сила,
получился скачок, равный величине этой силы.

Эпюра нормальных напряжений также строится вычислением значений напряжений по участкам: σ1 = N1 / A1= 22.5 МПа, σ2 = N2 / A2= - 27.5 МПа, σ3 = N3 / A3= - 55 МПа.

Теперь, при температурном воздействии, в выражения для реакций входят абсолютные значения
модуля упругости E и площади A. Вычислим величины реакций для конкретных данных: F = 10 кН,
A = 1 см2, t = 10o, E = 2*105 МПа,  =10-5 (сталь):

При отсутствии нагрева
реакции получаются равными
-2.5 кН и 7.5 кН соответственно.

При отсутствии нагрева значения напряжений получаются равными
37.5 МПа, - 12.5 МПа, и -25 МПа соответственно (вид эпюры напряжений см. в примере 1).
Таким образом, нагрев всего на 10о привел к увеличению сжимающей силы
и максимальных сжимающих напряжений
больше, чем в 2 раза.
Статически неопределимые системы всегда реагируют на изменение температуры изменением внутренних усилий.
Это же происходит при взаимных смещениях опор (неравномерная осадка опор).

15

сборки – В статически неопределимых системах несоответствие длин изготовленных элементов

проектным вызывает дополнительные внутренние усилия, которые могут заметно влиять на результат определения усилий от действия внешних сил. Более того, даже при отсутствии внешних сил, при сборке могут возникать начальные (монтажные) усилия. Общий порядок решения задачи сохраняется, но уравнения совместности деформаций (удлинений) содержат дополнительные удлинения (укорочения) необходимые для осуществления сборки неточно изготовленных элементов.
Пример 2. Абсолютно жесткая балка подвешивается на двух медных и одном стальном (Eм/Eс=1/2) стержнях одинаковой длины. Стальной стержень при изготовлении был сделан длиннее на величину . Определить монтажные усилия после сборки и усилия при нагружении силой F.

1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:

Rм

Rс

2. Статика : Составляем уравнение равновесия:

3. Геометрия: Задаем промежуточное положение балки и составляем
уравнение совместности деформаций:

4. Физика: Записываем соотношения связи деформаций с усилиями:

Подставим полученное соотношение
в уравнение равновесия:

Подставляем соотношения упругости в уравнения совместности:

В выражения для реакций входят абсолютные значения модуля упругости Eм , длины и площади стержней.
Вычислим величины реакций для конкретных данных: l = 2 м, A = 20 см2,  = 0.5 мм, Eм = 105 МПа :

медь

медь

сталь

a

a

l



Rм

Реакции от медных
стержней равны из-за
симметрии системы.

lм

lс

Знак минус присваивается, поскольку стальной
стержень должен укоротиться и внутреннее усилие должно быть отрицательным (сжатие).

Из этого же уравнения равновесия
следует:

При нагружении балки силой F посередине балка получает дополнительное перемещение б:

F

Уравнения равновесия, совместности деформаций и соотношения упругости принимают вид:

Подстановка соотношений
упругости в уравнения
совместности приводит
к ранее полученному
выражению для Rм=Rм(Rс).

Подстановка в уравнение равновесия дает:

Из выражения
Rм=Rм(Rс) :

После подстановки значений силы F =500 кН получаем Rс = 200 кН и Rм= 150 кН.

16

предыдущем примере рассматриваемая система была симметричной. Если система несимметричная по

геометрии, нагружению, материалам стержней, то перемещение жесткой балки при деформации будет не поступательное, а плоское (с поворотом вокруг некоторого центра). Рассмотрим решение такой задачи, подобной предыдущей, но со следующими данными: Левый медный стержень изготовлен короче остальных на величину , сила F приложена на расстоянии c > a от левого стержня. Найти усилия в стержнях.

1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:

R1м

Rс

2. Статика : Составляем уравнение равновесия:

3. Геометрия: Задаем произвольное наклонное положение балки и составляем
уравнения совместности деформаций:

4. Физика: Записываем соотношения связи деформаций с усилиями:

медь

медь

сталь

a

a

l



R1м

l1м

lс

F

17

с

А

φ

б

l2м

Получили полную систему уравнений, решающую данную задачу (8 уравнений и 8 неизвестных – 3 реакции
и 5 перемещений, два из которых поступательное перемещение балки, угловое перемещение - поворот).
Последние неизвестные можно исключить, составляя одно, но более сложное, уравнение совместности из подобия
треугольников в виде:

Поскольку решать вручную 5 уравнений тоже достаточно сложно можно
оставить первоначальную систему из 8 уравнений и решить ее численно, например, в системе
MathCAD, в которой не требуются какие-либо подстановки и преобразования (посмотреть).

Если направления одного или двух стержней отличны от вертикального, то эта задача становится
статически определимой (для плоской произвольной системы сил можно составить 3 независимых
уравнений равновесия) и несоответствие одного или двух размеров проектным не будут вызывать
начальных (монтажных) усилий (балка лишь изменит свое положение при сборке).

Пример 4. Пусть к такой системе добавлен еще один “лишний” стержень).

Система становится статически неопределимой, для которой можно составить 3 уравнения равновесия
и 4 уравнения совместности деформаций (вместе с 4 соотношениями упругости получается система 11
уравнений):

Теперь в соотношениях упругости длины 2-го и 3-го медных стержней:

Удлинения наклонных стержней определяются отрезками,
отсекаемые перпендикулярами, опущенными из нового
положения узла (конца стержня) на старое направление
стержня.

б

φ

l1м

l2м

l3м

lс

(Посмотреть решение этой
задачи в системе MathCAD)

бx

B1

B