Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6 Энергия и Момент Импульса ( Energy and Angular Momentum
Содержание
- 1. Лекция 6 Энергия и Момент Импульса ( Energy and Angular Momentum
- 2. Внешние и внутренние силы. Замкнутая система.
- 3. Замкнутая система = совокупность попарно взаимодействующих материальных
- 4. Элементарная работа силы. Работа силы на участке
- 5. Кинетическая энергия. Элементарную работу суммарной силы, действующей на
- 6. Работа консервативных сил (гравитация, электростатические силы, упругость)
- 7. Работа консервативной силы не зависит от формы
- 8. НЕ консервативные силы. Сила тренияРабота не
- 9. 1. Изолированная частица: T = Const2. Частица
- 10. Связь законов сохранения со свойствами пространства и времени.Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2
- 11. Момент импульса. Закон сохранения момента импульса Момент импульса. Закон сохранения момента импульса
- 12. Моментом импульса частицы относительно точки называется векторное
- 13. 1.Частица массы m движется по прямой со
- 14. 2. Частица движется по окружности радиуса r
- 15. Момент силы. Плечо силы. Моментом силы F
- 16. Пара сил. Пара сил = две равные
- 17. Производная момента импульса по времени Производная по
- 18. Момент импульса системы материальных точекМомент импульса системы
- 19. Закон сохранения момента импульсаЗакон изменения полного момента
- 20. Закон сохранения момента импульсаУравнение моментов: производная по
- 21. Закон сохранения момента импульсаПри отсутствии внешних сил
- 22. Движение в центральном поле силВ центральном поле
- 23. Силы, обратно пропорциональные квадрату расстояния от центра Движение в центральном поле сил.ПРИМЕР
- 24. Силы, обратно пропорциональные квадрату расстояния от центра
- 25. Космические скоростиПервой космической скоростью называется скорость, которую
- 26. Космические скоростиВторой космической скоростью называется минимальная скорость,
- 27. Связь законов сохранения со свойствами пространства и времени.Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2
- 28. Спасибо за внимание!Продолжение следует.Курс общей физики НИЯУ МИФИ
- 29. Закон сохранения момента импульсаУравнение моментов: производная по
- 30. Курс общей физики НИЯУ МИФИ
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Лекция 6
Энергия и Момент Импульса
(Energy and Angular Momentum)
Лектор:
доцент НИЯУ
МИФИ, к.ф.-м.н.,
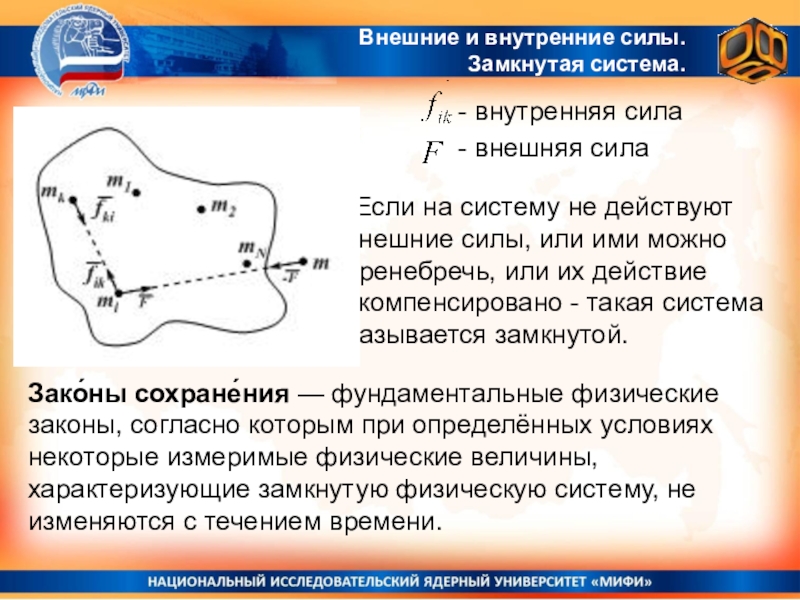
Слайд 2Внешние и внутренние силы.
Замкнутая система.
-
внутренняя сила
- внешняя сила
Если на систему
не действуют внешние силы, или ими можно пренебречь, или их действие скомпенсировано - такая система называется замкнутой.Зако́ны сохране́ния — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени.
Слайд 3Замкнутая система = совокупность попарно взаимодействующих материальных точек. Суммарное изменение
импульса а каждой паре равно нулю => суммарный импульс всей
системы сохраняется:Pсист = P1 + P2 + P3 + … = Σ Pi = Const
Закон сохранения импульса
для замкнутой системы частиц
dPсист / dt = Σ Fi = Fвнеш = Mdvc /dt = Md2rc /dt2
Движение составного объекта допустимо рассматривать, не вникая в его внутреннюю структуру и не учитывая взаимодействие его частей!
rс = Σ miri /M – радиус-вектор центра масс системы
Слайд 4Элементарная работа силы.
Работа силы на участке траектории
от
точки 1 до точки 2
Мгновенная мощность силы
Определение работы по известной
зависимости мощности от времениСредняя мощность силы
Дадим определения: Работа. Мощность.
Слайд 5Кинетическая энергия.
Элементарную работу суммарной силы, действующей на материальную точку, можно
представить в виде:
Величину T = mV2/2 называют кинетической энергией
материальной точки. Элементарная работа суммарной силы, действующей на материальную точку, идет на приращение ее кинетической энергии. И наоборот: за счет потери кинетической энергии тело может совершить механическую работу Энергия = мера способности тела произвести работу..
Слайд 6 Работа консервативных сил (гравитация, электростатические силы, упругость) НЕ зависит от
формы траектории, а только от начального и конечного положений частицы.
Для консервативных сил можно ввести понятие потенциальной энергии, зависящей исключительно от координат точки в поле консервативной силы. Работа консервативной силы равна разности потенциальных энергий объекта в начальной и конечной точках траектории: А12 = U1 - U2
В частности, для 2-х близких точек:
dА12 = U(r) - U (r+dr) = -(dr,dU/dr) =
= -dx(дU/дх)- dy(дU/дy)- dz(дU/дz)
Физический смысл имеет именно разность значений потенциальной энергии между разными точками. Абсолютное значение потенциальной энергии можно отсчитывать от любого уровня, какой удобен
Консервативные и неконсервативные силы.
Слайд 7Работа консервативной силы не зависит от формы траектории
,
….. и может пойти на приращение кинетической энергии точки
dAcons = dT = - dU
=> Сумма потенциальной и кинетической энергии точки, движущейся в консервативном поле сил, остается неизменной U + T = Const
Потенциальная энергия частицы
во внешнем силовом поле.
Слайд 8 НЕ консервативные силы. Сила трения
Работа не консервативных сил зависит
от формы траектории.
v
Fтр
Сила трения направлена против скорости движения материальной точки.
Элементарная работа силы трения равна.
dA = (F, dr) = -Fds,
где ds - элемент пройденного пути.
Работа силы трения на пути между точками 1 и 2 (и туда и обратно) равна.
A12 = - Fds,
.
1
2
Работа силы трения всегда отрицательна.
v
Fтр
Слайд 91. Изолированная частица: T = Const
2. Частица движется в потенциальном,
стационарном поле консервативных сил: Е = T +U = Const
3.Тело
движется в потенциальном, стационарном поле сил и на нее действует сила трения – уравнение баланса энергии Е1 (=U1+T1 ) = Е2 (=U2+T2) + А(против трения)
4. Замкнутая система взаимодействующих материальных точек, в которой нет НЕ консервативных сил.
Закон сохранения энергии
Некоторые частные случаи
Слайд 10Связь законов сохранения со свойствами пространства и времени.
Ландау Л.Д., Лифшиц
Е.М. «Механика», гл.2
Слайд 11Момент импульса.
Закон сохранения момента импульса
Момент импульса.
Закон сохранения
момента импульса
Слайд 12Моментом импульса частицы относительно точки называется векторное произведение радиус-вектора на
импульс частицы:
Длина перпендикуляра, опущенного из точки O на прямую, вдоль
которой направлен импульс частицы называется плечом импульса относительно точки ОМомент импульса. Плечо импульса
Слайд 131.Частица массы m движется по прямой со скоростью v. Момент
импульса частицы может изменяться только по модулю. Модуль момента импульса
равен M = mvl, причем плечо l остается неизменным.Момент импульса. Плечо импульса
ПРИМЕРЫ
Если на частицу не действуют силы – ее момент импульса не меняется ни по величине, ни по направлению:
M = [r, p]
Слайд 142. Частица движется по окружности радиуса r со скоростью v.
Модуль момента импульса относительно точки O равен M = pr·sin90°
= mvr. Вектор M перпендикулярен плоскости окружности, причем направление движения частицы и вектор M образуют правовинтовую систему. Плечо l = r = const и момент импульса может изменяться только за счет модуля скорости.Момент импульса. Плечо импульса
ПРИМЕРЫ
Когда частица движется в центральном поле сил, ее момент импульса не меняется ни по величине, ни по направлению:
M = [r, p].
Слайд 15Момент силы. Плечо силы.
Моментом силы F относительно точки О,
из которой проведен радиус-вектор r точки приложения силы называется псевдовектор:
1.
Вектор N перпендикулярен векторам r и F, и образует с ними правую тройку.2. Модуль момента силы можно представить в виде N = r F·sinα =l·F,
где l= r·sinα – плечо силы относительно точки O (длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила)
3. Точку приложения силы (в случае твердого тела) можно сдвигать вдоль линии действия силы: ни l ни N при этом не изменятся. Но величина и направление N зависят от выбора точки О
Слайд 16Пара сил.
Пара сил = две равные по модулю противоположно
направленные силы, не действующие вдоль одной прямой. Расстояние между прямыми,
вдоль которых действуют силы= плечо пары Суммарный момент сил, образующих пару, равен:Момент пары сил не зависит от точки отсчета O. Вектор момента пары сил перпендикулярен к плоскости, в которой лежат силы и численно равен произведению модуля любой из сил на плечо.
l = вектор, проведенный из точки приложения силы F1 в точку приложения силы F2
Слайд 17Производная момента импульса по времени
Производная по времени момента импульса
частицы относительно некоторой точки равна моменту силы относительно той же
точки.Слайд 18Момент импульса системы материальных точек
Момент импульса системы относительно точки =
векторная сумма моментов импульса всех частиц, входящих в систему:
Для каждой
частицы:Первое слагаемое – момент внешних сил, действующих на i-ую частицу, а второе – сумма моментов внутренних сил. Суммируя по всем частицам, получаем:
Слайд 19Закон сохранения момента импульса
Закон изменения полного момента импульса системы:
Двойная сумма
в правой части уравнения обращается в нуль, т.к. содержит парные
слагаемые вида:Скорость изменения момента импульса системы равна суммарному моменту внешних сил, днйствующих на систему:
Слайд 20Закон сохранения момента импульса
Уравнение моментов: производная по времени полного момента
импульса системы равна результирующему моменту внешних сил.
Пример: падение подпиленного
столба В точке опоры O действует неизвестная и, к тому же, меняющаяся со временем сила реакции N . Но момент этой силы относительно точки опоры равен нулю, и в уравнение моментов войдет только момент известной силы тяжести:
При отсутствии внешних сил
Для замкнутой системы M постоянен
Слайд 21Закон сохранения момента импульса
При отсутствии внешних сил
Для замкнутой системы
M постоянен
Закон сохранения момента импульса: момент импульса замкнутой системы материальных
точек остается постоянным. Момент импульса остается постоянным и для незамкнутой системы при условии, что суммарный момент внешних сил равен нулю.
Слайд 22Движение в центральном поле сил
В центральном поле силы, действующие на
частицу в любой точке направлены на центр поля, а модуль
силы зависит только от расстояния до этого центра.Момент импульса частицы относительно центра (т. 0) будет сохраняться
При движении частицы в центральном поле сил ее радиус-вектор остается все время в одной плоскости. В этой же плоскости лежит все время вектор p. Траектория частицы представляет собой плоскую кривую.
Момент перпендикулярен к плоскости, образованной r и p
M = const => плоскость движения фиксирована
Слайд 23Силы, обратно пропорциональные квадрату расстояния от центра
Движение в центральном
поле сил.
ПРИМЕР
Слайд 24Силы, обратно пропорциональные квадрату расстояния от центра
Движение в центральном
поле сил.
ПРИМЕР
Траектория частицы = коническое сечение, т.е. либо эллипс, либо
параболу, либо гиперболу. α > 0 (отталкивание): Гипербола. При Mz= 0 вырождается в прямую
α < 0 (притяжение): Эллипс при E < 0, гипербола при E > 0, парабола при E = 0
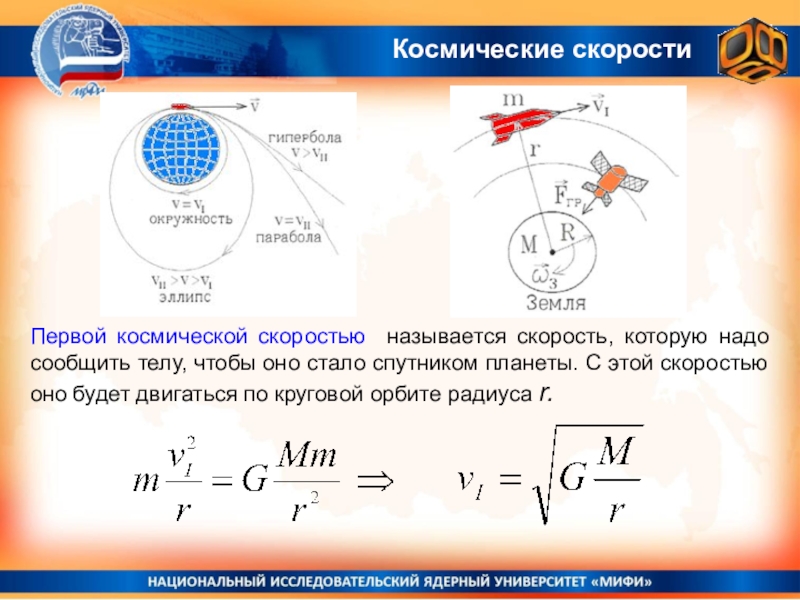
Слайд 25Космические скорости
Первой космической скоростью называется скорость, которую надо сообщить телу,
чтобы оно стало спутником планеты. С этой скоростью оно будет
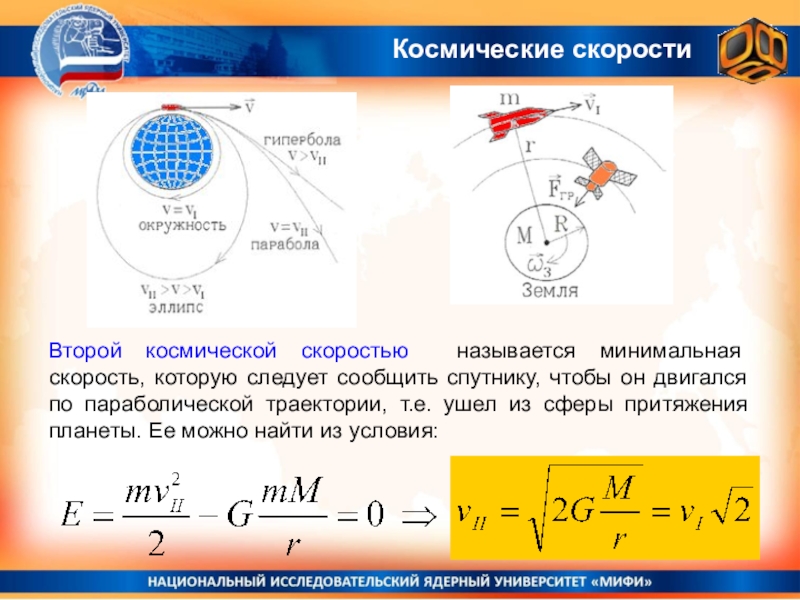
двигаться по круговой орбите радиуса r.Слайд 26Космические скорости
Второй космической скоростью называется минимальная скорость, которую следует сообщить
спутнику, чтобы он двигался по параболической траектории, т.е. ушел из
сферы притяжения планеты. Ее можно найти из условия:Слайд 27Связь законов сохранения со свойствами пространства и времени.
Ландау Л.Д., Лифшиц
Е.М. «Механика», гл.2
Слайд 29Закон сохранения момента импульса
Уравнение моментов: производная по времени полного момента
импульса системы равна результирующему моменту внешних сил.
Пример: падение подпиленного
столба В точке опоры O действует неизвестная и, к тому же, меняющаяся со временем сила реакции N . Но момент этой силы относительно точки опоры равен нулю, и в уравнение моментов войдет только момент известной силы тяжести:
При отсутствии внешних сил
Для замкнутой системы M постоянен