Лекция №7

данная фигур вместе с осями прямоугольных координат, к которым она

Плоскость аксонометрической проекции называют картинной плоскостью.

Направление проецирования может составлять с картинной плоскостью острый или прямой угол.

осям). Предмет располагается так, что его главные направления не являются

Различают косоугольную (проецирующие лучи наклонены к аксонометрической плоскости и прямоугольную, когда проецирующие лучи перпендикулярны аксонометрической плоскости аксонометрии

Коэффициентом искажения u, v и w называется отношение аксонометрических координат к натуральным.

При данном направлении проецирования сумма коэффициентов искажения есть величина постоянная

u 2 + v 2 + w 2 = A = const

При прямоугольном проецировании А=2, при косоугольном проецировании А=2+ctg2, где  - угол наклона направления проецирования.

В зависимости от наклона осей координат аксонометрические проекции классифицируются следующим образом:
Триметрические проекции u ≠ v ≠ w;
Диметрические проекции u = v ≠ w;
Изометрические проекции u = v = w.

множитель так, чтобы один(или несколько) из показателей был равен единице.

Приведенные показатели обозначаются U, V, W

Множитель на который умножаются теоретические показатели искажения для получения приведенных коэффициентов называется коэффициентом приведения

Аксонометрическое изображение, у которого u=v=w=0,82 называется теоретической изометрией

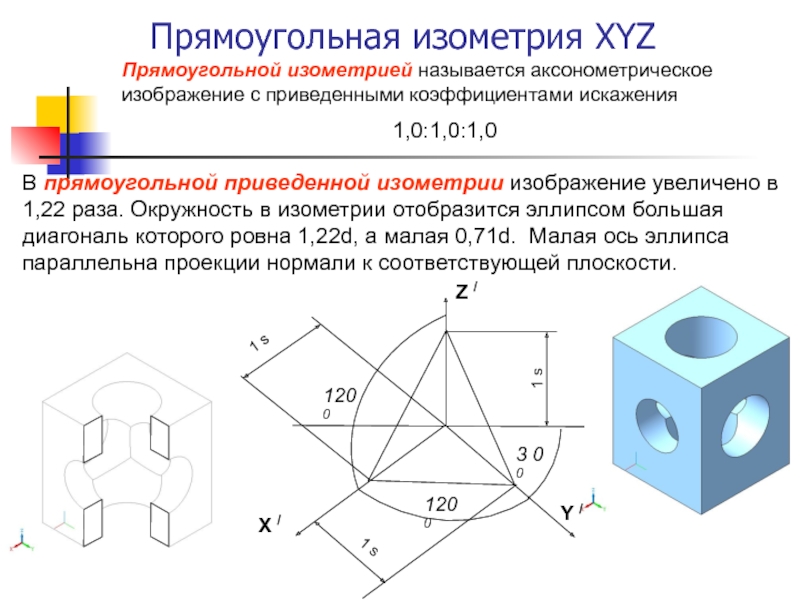
Для упрощения построений пользуются приведенной (стандартной) изометрией для которой приведенные коэффициенты искажения равны:

U = V = W = 1,0

Аксонометрическое изображение, у которого u=v=0,94, w=0,47 называется теоретической диметрией

Для упрощения построений пользуются приведенной (стандартной) диметрией для которой приведенные коэффициенты искажения равны:

U = V = 1,0;

W = 0,5

Аксонометрическое изображение, у которого u=w=1, v=0.5 называется теоретической фронтальной диметрией

следов всегда остроугольный;
Три выходящие из одной точки полупрямые на плоскости

искажения
1,0:1,0:1,0
В прямоугольной приведенной изометрии изображение увеличено в 1,22 раза.

1,0:0,5:1,0
В прямоугольной приведенной диметрии изображение увеличено в 1,06 раза. Окружность