Лекция №7 по курсу Машинная арифметика в рациональных числах Москва, 2020

+ c = 0
Формулы корней квадратного уравнения достаточно сложны по

числу и набору действий:

Поэтому естественно предположить, что при решении поставленной задачи возможна ситуация, при которой произойдет потеря точности.

в числителе обязательно будет разность чисел.
Пусть b>0, тогда при ac

числа b и близки и формула для x2 может привести к грубой ошибке.

Здесь можно полностью устранить причину возможной ошибки за счет тождественного преобразования для х2

Получили другую формулу для одного из корней квадратного уравнения

Эта формула уже не содержит вычитания близких чисел, тем самым устранена причина возможной грубой ошибки.

х1. Соответствующими преобразованиями можно и ее привести к виду:
Очевидно, что

новые формулы для корней квадратного уравнения пригодны и для «нормальных случаев», когда разность близких чисел не возникает. Т.о. проводить анализ близости соответствующих чисел нет необходимости. Достаточно, определив знак b, выбрать для вычисления каждого корня ту формулу, в которой разности чисел нет.

что эта задача хорошо обусловлена.

при x

x= -15.
Верное значение e-15 =1 / e15  0.000000305902

1. Традиционные вычисления
После выполнения 82 итераций было получено: e-15  0.000000256502
Относительная погрешность
составила 19,2%.

2. Решение
e-x = 1/ ex

коэффициентами
Нестационарное уравнение теплопроводности:
.
Уравнение теплопроводности описывает распространение тепла вдоль стенок труб

теплообменных устройств, поверхностей нагрева котлов, и других объектов.

- коэффициент температуропроводности

При

максимальная относительная погрешность решения

системы методом Гаусса-Зейделя составила около 100% при числе итераций порядка 5000.
Физическая интерпретация этих параметров может быть такой: ищется распределение температуры магистрального трубопровода длиной 1 км через каждые 1 метр, каждые 3 часа.
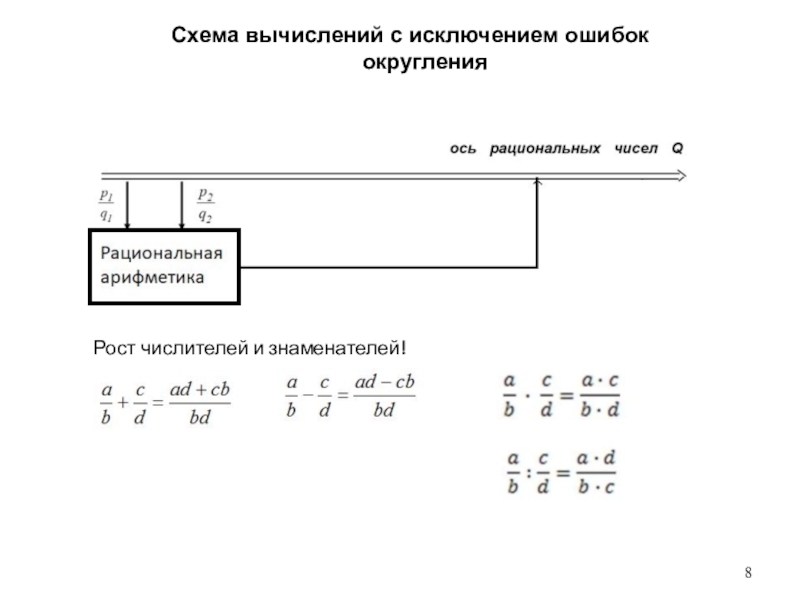
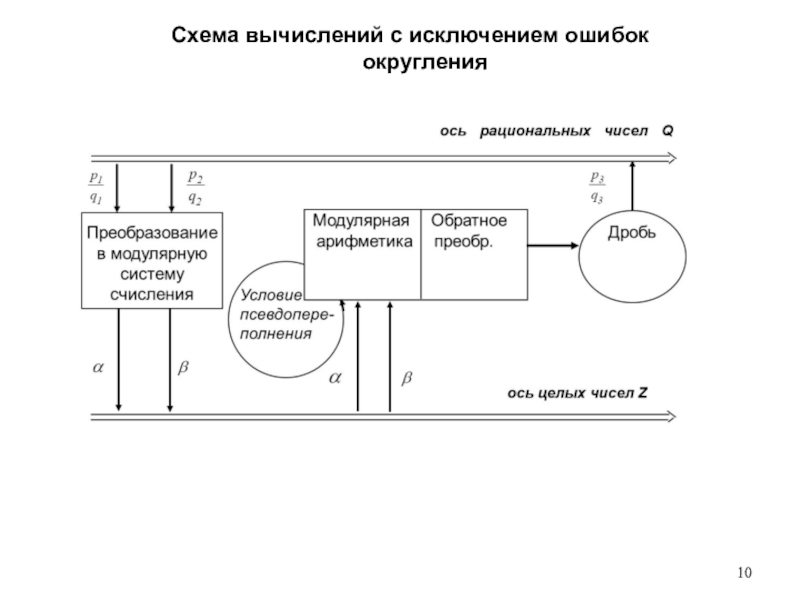
Применение высокоточных вычислений позволило получить решение системы с требуемой точностью

Система конечно-разностных линейных уравнений:

К настоящему времени модулярная арифметика

использовалась как средство повышения быстродействия в криптографии, нейронных сетях, цифровой обработке сигналов и др.
Проведенные исследования показали качественно новые возможности применения модулярной арифметики в повышении точности вычислений и ослаблении зависимости времени вычислений от точности, для некоторых частных задач:
решение дифференциальных уравнений методами Рунге-Кутта,
нахождение скалярного произведения векторов,
решения систем линейных уравнений методами Гаусса-Зейделя,
релаксации,
дискретном преобразовании Фурье .

обратных матриц. Например, таких как, g-обратная матрица Мура-Пенроуза. Многие

алгоритмы требуют умения распознавать значение численного ранга, а это является трудной задачей при наличии ошибок округления.
2. Целочисленное решение систем линейных уравнений. Примером могут служить построение оптимальных решений в задачах целочисленного программирования.
3. Точное вычисление характеристического многочлена матрицы. Вследствие ошибок округления будут получены приближенные значения коэффициентов. Если многочлен плохо обусловлен, то корни "приближенного» характеристического уравнения могут быть плохими приближениями к корням истинного уравнения.
4. Обращение матриц Гильберта, Адамара и др. особо чувствительных к ошибкам округления.
5. Для решения промежуточных между классами корректных и некорректных задач.
Класс задач, изменяющих корректность при решении. Это расчет устойчивости систем управления, выч. собств. знач. систем лин. одн. урав. и др.

числа,
рациональные числа
комплексные числа с рациональной мнимой и вещественной

частью

Иррациональные числа представлять в виде цепных дробей.

Точное значение 10/7 это [1,2,3].
Приближенное значение [1,2]

Вычисления с иррациональными числами с контролируемой точностью.

расширенного алгоритма Евклида

чисел - единое представление чисел различной природы (целых, комплексных)
Задачи на модулярную

арифметику Найти последние 2 цифры числа 4^30.

– существует только одно число, имеющее остатки по модулям в

диапазоне до произведения модулей минус один