Слайд 1Лекция4
Закон сохранения энергии
Принцип относительности в механике
Слайд 2 Потенциальная энергия
Потенциальная энергия –механическая энергия системы
тел,
определяемая их взаимным расположением и
характером сил взаимодействия между ними.
Если на
частицу действует консервативная сила , то каждой точке поля сил можно сопоставить значение некоторой функции координат , которая называется потенциальной энергией частицы в поле данной консервативной силы. Если консервативная сила совершает работу dA, то происходит изменение взаимного расположения тел системы и потенциальная энергия U убывает на величину dA, то есть dA=-dU
Если знать потенциальную энергию, можно вычислить работу, совершаемую силами поля над телом с массой при перемещении его из положения 1 в положение 2.
Слайд 3 Эта работа может быть выражена через разность значений потенциальной
энергии в указанных точках:
Полученное выражение означает, что работа консервативных сил
равна убыли потенциальной энергии.
Из определения следует, что потенциальная энергия известна с точностью до определенной постоянной. Так как определена только ее разность, то к выражению можно добавить или вычесть любую постоянную величину. При этом величина , конечно, меняется, но работа консервативной силы останется одной и той же. Поэтому в каждом конкретном случае договариваются о начале отсчета потенциальной энергии: в какой именно точке следует считать из соображения удобства.
Слайд 4Рассмотрим примеры рассчета потенциальной энергии.
Пример 1. Потенциальная энергия в однородном
поле сил тяжести.
Нулевое значение U удобно выбрать при
h =0. Тогда потенциальная энергия в точке 1 вычисляется по формуле:
Так как начало отсчета выбирается произвольно, то потенциальная
энергия может быть отрицательной.
На приведенном рисунке U=0 на высоте H,
поэтому потенциальная энергия в точке 1
отрицательна:
Конкретный вид функции зависит от характера
силового поля.
Слайд 5Пример 2. Потенциальная энергия гравитационного
притяжения.
Работа,
совершаемая силой тяготения по перемещению тела массой m из точки с радиусом до точки с радиусом была найдена ранее, она равна:
Нулевое значение потенциальной энергии выбирается при Тогда работа силы тяготения при перемещении тела из точки с радиусом на бесконечность равна:
Отсюда находим потенциальную энергию гравитационного притяжения:
Слайд 6 Пример 3. Потенциальная энергия деформированного
тела.
Рассмотрим в качестве упруго деформированного тела пружину с коэффициентом жесткости k ; положение нерастянутого края пружины обозначим x = 0, тогда при удлинении его координата
будет равна x. Соответствующее значение упругой силы:
Нулевое значение потенциальной энергии U=0 выбираем при x = 0. Тогда потенциальная энергия упругой деформации:
Слайд 7В заключение еще раз: Потенциальная энергия системы является функцией состояния
системы. Она зависит только от конфигурации системы и ее положения
по отношению к внешним телам.
График зависимости U от х показан на рисунке
х
Слайд 8Связь между потенциальной энергией и силой
Пространство, в котором
действуют потенциальные силы, называется потенциальным полем. Каждой точке потенциального поля
соответствует некоторое значение силы F , действующей на тело, и некоторое значение потенциальной энергии U . Значит между F и U должна быть связь.
Работа консервативной силы:
Где:
Тогда:
Если:
то для одномерного случая
Откуда
Слайд 9По аналогии для двух остальных проекций силы F получаем:
Связь
консервативной силы с потенциальной энергией принимает вид:
Оператор в правой части
этого выражения называют градиент или набла, (понятие векторного анализа):
Тогда окончательно получаем:
Слайд 10Закон сохранения механической энергии
Закон сохранения энергии – результат обобщения
многих
экспериментальных данных.
Идея этого закона принадлежит Ломоносову, изложившему закон сохранения материи
и движения, а количественная формулировка закона сохранения энергии дана Ю. Майером и Г. Гельмгольцем.
Рассмотрим закон сохранения энергии
Слайд 11Рассмотрим систему материальных точек, на каждую из которых действуют:
внутренние консервативные
силы,
внешние консервативные силы, а также
внешние неконсервативные силы.
Применяя
к этой системе второй закон Ньютона можно заключить, что
приращение кинетической энергии системы dK, а также элементарное приращение потенциальной энергии dU этой системы, представляющие собой в сумме изменение полной механической энергии системы при переходе из одного состояния в другое, будет равно работе, совершенной в ходе такого перехода внешними неконсервативными силами.
Слайд 12Если внешние неконсервативные силы отсутствуют, то:
откуда:
т.е. полная механическая энергия системы
сохраняется постоянной. Полученное выражение представляет собой закон сохранения механической энергии:
В
системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.
Слайд 13Итак, в консервативных системах полная механическая
энергия остается постоянной. Могут происходить
лишь
превращения кинетической энергии в потенциальную и
обратно в эквивалентных количествах
так, что полная
энергия остается неизменной.
Закон сохранения механической энергии связан с
однородностью времени.
Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от какого момента отсчитывается время.
Слайд 14 Общефизический закон сохранения энергии
Существует еще один вид систем –
диссипативные системы, в которых механическая энергия постепенно уменьшается за счет
преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяние) энергии. Строго говоря, все системы в природе являются диссипативными. Работа дисипативных сил всегда отрицательна, поэтому, из полученного ранее выражения
видно, что при наличии диссипативных сил полная механическая энергия уменьшается.
Слайд 15Итак, в системе, в которой действуют также неконсервативные силы, (например,
силы трения,) полная механическая энергия системы не сохраняется. Следовательно, в
этих случаях закон сохранения механической энергии не справедлив.
Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида.
Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.
В этом и заключается сущность общефизического закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.
Слайд 16Этот закон выражает количественную и качественную сторону взаимного превращения различных
форм движения друг в друга.
Закон сохранения и превращения энергии –
фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
Слайд 17 Галилео Галилей
(Galileo Galilei)
астроном, философ
и физик.
важнейшие роботы
улучшение телескопа
разнообразие астрономических наблюдений первый закон движения
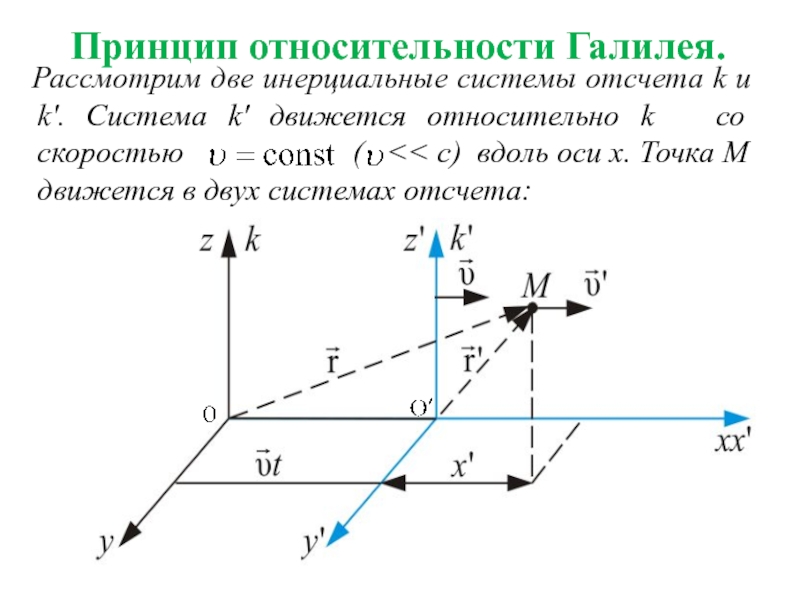
Слайд 18 Принцип относительности Галилея.
Рассмотрим две инерциальные системы
отсчета k и k'. Система k' движется относительно k
со скоростью ( << c) вдоль оси x. Точка М движется в двух системах отсчета:
Слайд 19 Запишем движение точки М в этих двух системах,
задав это движение радиус-векторами и
соответственно в системе k и k’ :
- радиус-вектор, определяющий положение точки системы в системе отсчёта k.
К моменту времени t (t=t’):
Спроецировав на координатные оси, запишем в скалярной форме:
- преобразо-
вания
Галилея
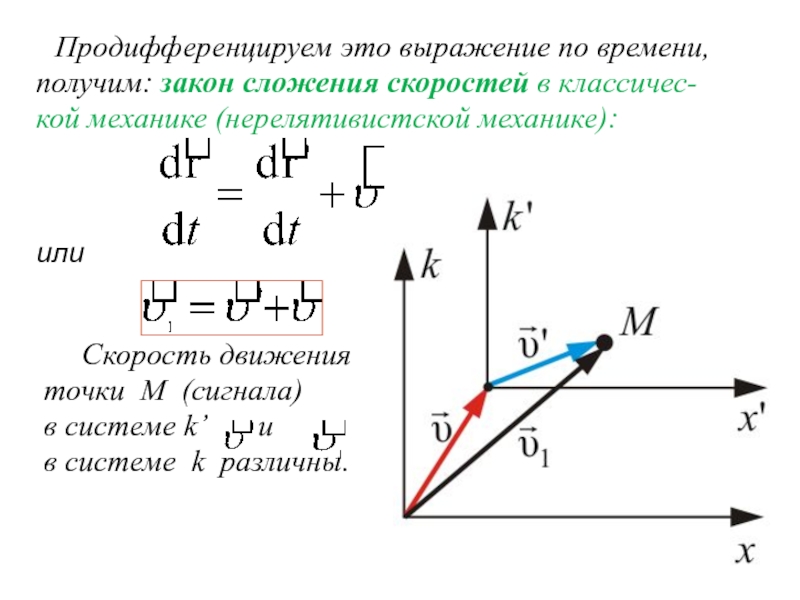
Слайд 20 Продифференцируем это выражение по времени,
получим: закон сложения
скоростей в классичес-
кой механике (нерелятивистской механике):
или
Скорость
движения
точки М (сигнала)
в системе k’ и
в системе k различны.
Слайд 21 Ускорение в системе отсчета k
Получили инвариантность ускорения (одинаковость во всех инерциальных системах отсчёта- ИСО)
Изучение медленных ( ) механических
движений показало, что
= , .
Таким образом, масса и сила также являются
инвариантами при переходе из одной ИСО в
другую.
Слайд 22 Уравнения движения частицы имеют одинаковый
вид во
всех ИСО:
и
Обобщение полученных выше результатов формулируется в виде принципа относительности Галилея (Г. Галилей, 1636 г.): законы механики одинаковы во всех инерциальных системах отсчёта, поэтому никакими механическими опытами внутри ИСО, изолированных от внешних воздействий, невозможно обнаружить её движение с постоянной скоростью. К этому принципу Г. Галилей пришёл на основе опыта и мысленных экспериментов. Принцип относительности Галилея утверждает равноправие всех ИСО
Слайд 23 Основные постулаты СТО
(специальной теории относительности)
Первый постулат теории
относительности.
Все законы природы одинаковы
в инерциальных
системах отсчета.
Второй постулат теории
относительности.
Скорость света c=3· м/с в вакууме
одинакова во всех инерциальных
системах отсчета и является макси-
мальной для любого физического
взаимодействия (сигнала).
.
Альберт
Эйнштейн
1879-1955
Слайд 24Второй постулат связан с поведением пространства и времени. Они уже
зависят друг от друга и образуют единое пространство-время с координатами
. Это четырехмерное пространство. Квадрат расстояния между двумя точками в таком пространстве
называется интервалом и является инвариантом при переходе от одной ИСО к другой.
Введем некоторые обозначения:
- релятивистский фактор.
Слайд 25 ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Для систем отсчёта
и преобразования
Лоренца имеют вид при (V
~ c):
преобразований Галилея ( принцип соответствия):
Далее рассмотрим следствия из преобразований Лоренца.
Слайд 27 Сокращение длины
Рассмотрим стержень, расположенный вдоль оси
x’ и покоящийся относительно системы K’. Длина его в этой
системе равна
Для определения длины стержня в системе K нужно отметить координаты концов стержня в один и тот же момент времени t.
Итак, длина стержня l в системе k меньше длины l′ в системе k′
Слайд 28 Замедление времени
Пусть в
одной и той же точке x′1= x′2= x′ системы K′
происходят два события в моменты времени t′1 и t′2. Этим событиям соответствуют в системе K моменты времени t1 и t2:
- это собственное время
Слайд 29Cобственное время всегда меньше времени, отсчитываемого по часам в системе
К. С точки зрения наблюдателя в системе К часы в
системе отстают. Но дело, конечно, не в часах. Замедляются все процессы во всех телах, находящихся в .
ПРЕОБРАЗОВАНИЕ И СЛОЖЕНИЕ СКОРОСТЕЙ
Пусть , тогда
Скорость света
одинакова во
всех системах
отсчета
Слайд 30Общефизический принцип относительности
Принцип относительности в трактовке Эйнштейна:
“Законы природы,
по которым изменяются состояния физических систем, не зависят от того,
к какой из инерциальных систем отсчёта относятся эти изменения”.
В релятивистской механике импульс частицы:
где для сохранения классической формулы
вводят понятие релятивистской массы :
- масса покоя
(при V= 0)
Слайд 31 Релятивистская энергия частицы
в отсутствие действия внешних
физических
полей:
Связь между импульсом и энергией :
- формула Эйнштейна
- энергия покоя частицы ( V= 0)
Кинетическая энергия частицы K определяется выражением:
В области малых скоростей кинетическая энергия:
Слайд 32РЕЛЯТИВИСТСКИЕ ИНВАРИАНТЫ
Скорость света в вакууме - c
Интервал
Собственное время
, но
,
следовательно,
Выражение, связывающее энергию и импульс
Последнее выражение легко получить из четырех вектора
Слайд 33Принцип соответствия
Суть этого принципа в том, что любая
новая
теория, претендующая на более глубокое описание
физической действительности и на
более широкую
область применимости, чем старая теория, должна
включать в себя эту старую теорию как предельный случай. В полном согласии с принципом
соответствия преобразования
Лоренца переходят в преобразо-
вания Галилея, а релятивистский
закон динамики переходит в
классический закон Ньютона.