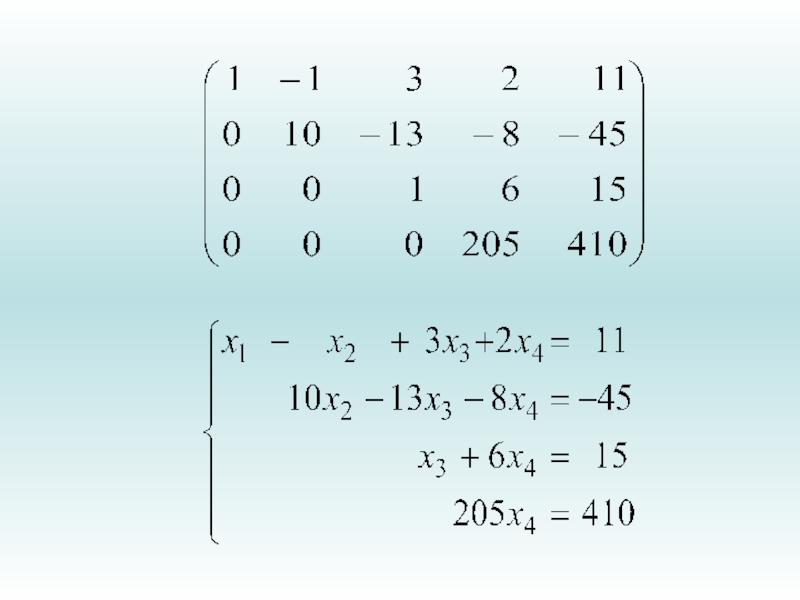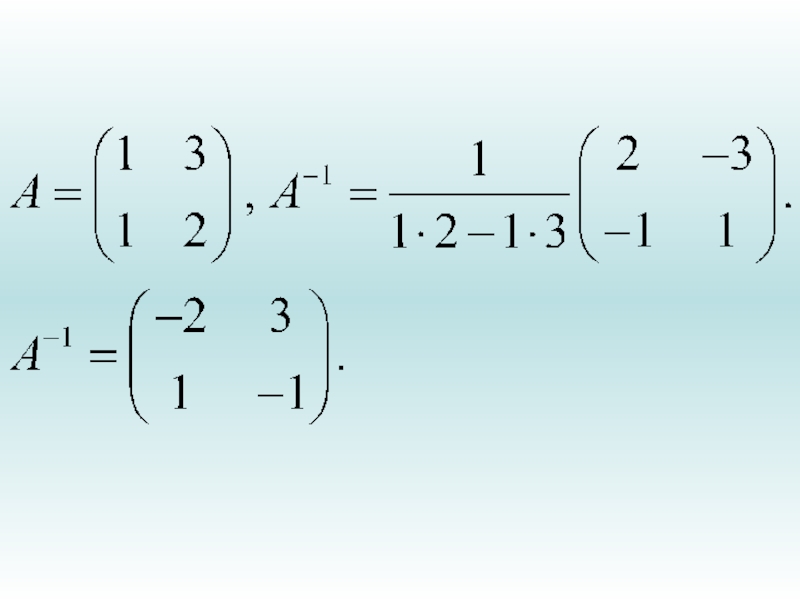Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра
Содержание
- 1. Линейная алгебра
- 2. Линейная алгебраЛитература1. Б.Ш.Гулиян, Р.Я.ХамидуллинМатематика . Базовый курс, М. ООО«Маркет ДС Корпорейшн,2008.
- 3. ВведениеЛинейная алгебра - это теория линейных алгебраических
- 4. Решение системы линейных уравнений со многими неизвестными !
- 5. Линейная алгебра проявляет единство двух основных подходов
- 6. Линейность представляет весьма общее понятие. Все линейные
- 7. Однородность означает, что если х приводит к
- 8. С математической точки зрения линейные модели имеют
- 9. Модуль вектораКак уже упоминалось, очень важной характеристикой
- 10. Операции над векторамиМы также будем записывать вектор
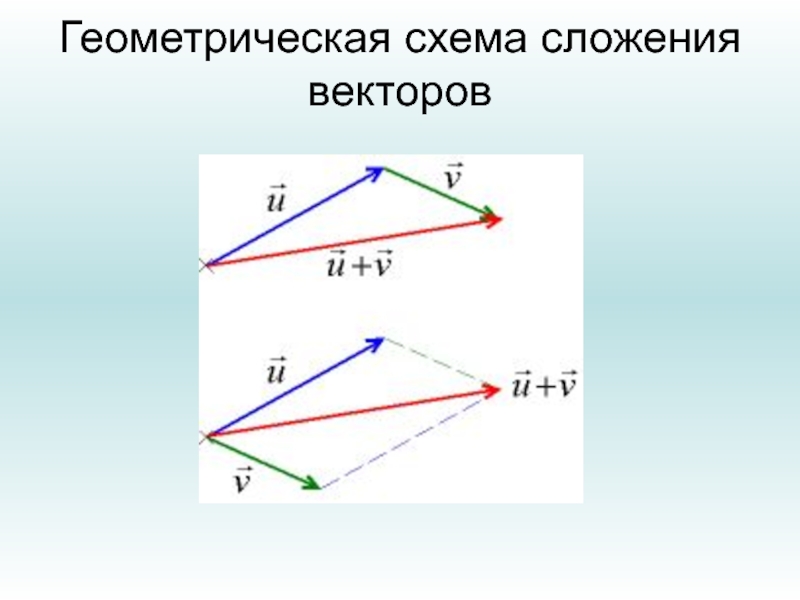
- 11. Геометрическая схема сложения векторов
- 12. ВекторыВ пространстве имеется так называемый естественный или
- 13. Векторыпредставим в виде Эти две записи (правая
- 14. Линейная зависимость векторов Множество векторов {an}
- 15. Линейная зависимость векторов Если векторы линейно зависимы,
- 16. Пример линейно зависимых векторов Пример. Вектора на
- 17. n-мерное векторное пространство . Базис Совокупность n
- 18. Единичным вектором является вектор, у которого длина
- 19. Скалярное произведение векторовВекторы можно перемножать. Допустим, что
- 20. Скалярное произведение векторовназывают скалярным произведением векторов и
- 21. Скалярное произведение векторов А⋅В
- 22. Скалярное произведение векторовВекторы a и b называются
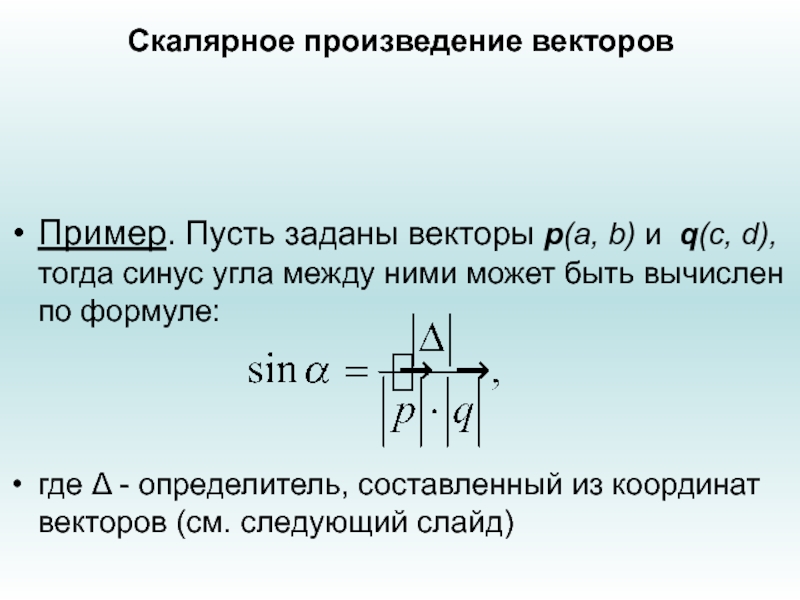
- 23. Скалярное произведение векторовПример. Пусть заданы векторы р(a,
- 24. ОпределительОпределитель Δ равен:Замечание
- 25. Площадь параллелограммаУтверждение. Пусть ABCD произвольный параллелограмм, заданный
- 26. Равенство нулю определителя Определитель треугольной матрицы равен произведению диагональных элементов.
- 27. Определитель треугольной матрицыНапример. Рассмотрим пример нахождения определителя.
- 28. треугольному виду( из 2-й строки вычтем 1-ую):
- 29. Значение этого определителя не надо искать, т.к. его величина равна нулю(!).Третий столбец пропорционален первому.
- 30. ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦМатрица – это определенным образом
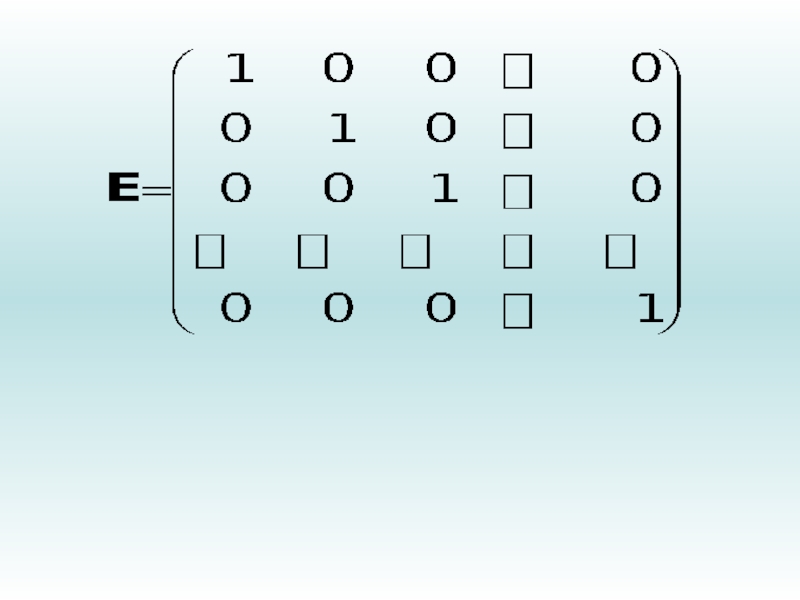
- 31. ОСНОВНЫЕ ПОНЯТИЯМатрица состоит из элементов – чисел.Нулевой
- 32. Слайд 32
- 33. ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦОсновные понятия. Рассмотрим систему m линейных алгебраических уравнений с n неизвестными:
- 34. Решением системы называется упорядоченный набор из n
- 35. Если число уравнений системы совпадает с числом
- 36. двух неизвестных с учетом их
- 37. Если применить рассмотренные элементарные преобразования к матрице,
- 38. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯВАЖНО !
- 39. ЧТО ТАКОЕ МАТРИЦА ??
- 40. Далее мы будем основываться на системе
- 41. Можно сказать что, матрица – это прямоугольная
- 42. Числа aij (i = 1,2, …, m; j =1, 2, …, n) называются элементами матрицы.
- 43. Представленная матрица (2) называется матрицей коэффициентов системы
- 44. На множестве матриц вводится понятие равенства. Две
- 45. На множестве согласованных (одинаковых) матриц вводится операция
- 46. Под произведением αA понимается матрица (αaij), то
- 47. Сложение матриц
- 48. Операция сложения матриц коммутативна и ассоциативна (как
- 49. тех матриц, для которых выполняется следующее условие:
- 50. т.е. элемент cij матрицы C равен сумме
- 51. Слайд 51
- 52. Умножение матрицС=АВ
- 53. Структура произведения
- 54. x11 x12
- 55. Если произведения AB и BA одновременно определены,
- 56. Мы получили в результате две неравные матрицы.Если
- 57. 2) α (A + B) = αA
- 58. Метод Гаусса решения систем линейных уравнений
- 59. Метод Гаусса решения систем линейных уравнений Метод
- 60. Метод Гаусса решения систем линейных уравнений Рассмотрим
- 61. Метод Гаусса решения систем линейных уравнений Решение
- 62. Метод подстановки и другое неизвестное - y
- 63. Метод сложения Рассмотрим пример. Из одного уравнения вычитаем/складываем другое (это элементарное преобразование), например
- 64. Метод Гаусса решения систем линейных уравненийИдея состоит
- 65. Метод Гаусса решения систем линейных уравненийПри решении
- 66. Метод Гаусса решения систем линейных уравнений являются
- 67. Метод Гаусса решения систем линейных уравненийПредположим, что нам надо решить систему линейных уравнений, например:
- 68. метод1. Устанавливается строка, с помощью которой будем
- 69. В первом уравнении ведущий или разрешающий
- 70. Первое уравнение у нас остается без изменения.
- 71. Используя второе уравнение из новой системы, исключаем
- 72. В итоге после элементарных преобразований получаем эквивалентную систему:
- 73. Из третьего уравнения находим х3 =3. Подставляя
- 74. Окончательно находим решение системы х1 =1, х2
- 75. нулю, а правая часть не будет равна нулю, то данная система несовместна.Метод Жордана-ГауссаРешить систему уравнений:
- 76. Запишем матрицу и приведем ее к разрешенному
- 77. Из третьей вычитаем первую:
- 78. К первой прибавляем третью (6 раз)
- 79. Из третьей вычитаем первую:
- 80. Ко второй прибавляем первую (5 раз):
- 81. В результате исходная система принимает следующий вид:В
- 82. Метод Гаусса решения систем линейных уравненийРассмотрим квадратную систему линейных уравнений, например:
- 83. Для того, чтобы избавиться от х1 мы
- 84. 2) наша задача исключить x1 из второго и
- 85. Продолжим. Преобразуем полученную матрицу следующим образом:1) первые
- 86. 2) вместо третьей строки запишем разность между второй
- 87. Теперь исключим неизвестную x3 из четвертого уравнения.
- 88. Слайд 88
- 89. Очевидно, мы получили треугольную систему.Отсюда находим :
- 90. То есть наша матрица представляет собой в
- 91. Транспонирование матрицы.При транспонировании матрицы строки и столбцы меняются местами. Операция транспонирования обозначается звездочкой или индексом Т.
- 92. ОБРАТНАЯ МАТРИЦА
- 93. ОБРАТНАЯ МАТРИЦАОбратная матрица вводится по аналогии с
- 94. Заметим, что не всякая квадратная матрица имеет
- 95. необходимо воспользоваться формулой:
- 96. По этой формуле, если разность ad-bc не
- 97. Слайд 97
- 98. Свойства обратной матрицыЕ-1 =Е;(А-1) -1 =А.Для получения
- 99. ОПРЕДЕЛИТЕЛЬ
- 100. Слайд 100
- 101. Определение детерминанта detКвадратной матрице А (порядка n)
- 102. Определение детерминанта detКаждый член определителя равен произведению
- 103. Свойства определителяОпределитель не меняется при транспонировании матрицы.Определитель
- 104. Свойства определителяОпределитель меняет знак, если две строки
- 105. кроме i–ой такие же, а
- 106. Свойства определителя обратной матрицыdet(AВ)=det(A) det(В)det(A-1 )=1/det (A)
- 107. МЕТОД КРАМЕРА
- 108. Рассмотрим теперь систему трех линейных уравнений с
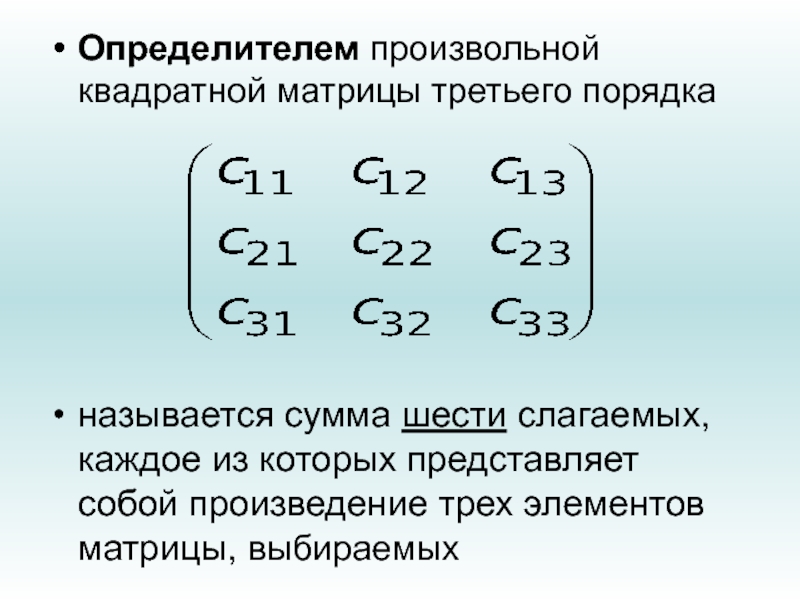
- 109. Определителем произвольной квадратной матрицы третьего порядканазывается сумма
- 110. по следующему правилу: три произведения элементов, стоящих
- 111. с основаниями, параллельными побочной диагоналиберутся со знаком
- 112. Нахождение определителя Δ матрицы А третьего порядка
- 113. Определитель третьего порядка обозначается в вертикальных отрезках:
- 114. Вернемся к решению нашей системы (6). Например
- 115. Слайд 115
- 116. Обратите внимание, что в определителе Δ1 первый
- 117. Из равенств (7) следует, что если Δ ≠ 0, то решение определяется единственным образом (формулы Крамера):
- 118. ОПРЕДЕЛИТЕЛЬ НЕ РАВЕН НУЛЮ!
- 119. Решение системы уравнений методом Крамера ОТВЕТ
- 120. Слайд 120
- 121. Слайд 121
- 122. Ранг матрицыНаибольший из порядков отличных от нуля
- 123. Слайд 123
- 124. Теорема Кронекера-КапеллиСистема линейных алгебраических уравнений совместна, если ранг матрицы системы равен рангу расширенной матрицы.
- 125. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Линейная алгебра
Литература
1. Б.Ш.Гулиян, Р.Я.Хамидуллин
Математика . Базовый курс, М. ООО
«Маркет ДС
Корпорейшн,2008.
Слайд 3Введение
Линейная алгебра - это теория линейных алгебраических структур (линейных пространств,
линейных отображений и т.д.). Результаты линейной алгебры, теории матриц необходимы
во многих областях. Основное внимание мы будем уделять решению систем линейных уравнений со многими неизвестными.Слайд 5Линейная алгебра проявляет единство двух основных подходов математики- абстрактности и
приложимости. Для менеджеров и экономистов это путь к линейному программированию.
Слайд 6Линейность представляет весьма общее понятие. Все линейные модели, процессы и
явления обладают свойствами аддитивности и однородности. Аддитивность в математическом смысле
означает следующее: если действие х приводит к эффекту α, а действие у приводит к эффекту β , то совместное действие х+у приводит к совместному эффекту α+β .Слайд 7Однородность означает, что если х приводит к эффекту α, то
х+х приводит к эффекту α+α, т.е. в общем случае kx
приводит к эффекту kα .линейность
аддитивность
однородность
Слайд 8С математической точки зрения линейные модели имеют определенные преимущества, т.к.
линейные задачи всегда решаются (в том смысле, что не может
сложиться ситуация, когда не бывает известно имеет ли решение задача).Еще в 4 в. до н.э. Тамарид решал систему уравнений. Баше де Мезирак [1587-1638] предложил решение в целых числах системы с двумя уравнениями.
Почти все линейные модели сводятся к системам алгебраических линейных уравнений или неравенств.
Слайд 9Модуль вектора
Как уже упоминалось, очень важной характеристикой вектора является его
длина (модуль). Модуль вектора по определению равен (обобщенная теорема Пифагора)
Числа х1, х2, х3 называются компонентами или координатами вектора.
Слайд 10Операции над векторами
Мы также будем записывать вектор кратко буквой со
стрелкой. На множеств векторов вводится операция сложения и умножения на
скаляр (т.е. векторное пространство), которые определяются так:Если хотя бы одна операция не определена, то это не векторы. Определена также геометрическая схема сложения.
Слайд 12Векторы
В пространстве имеется так называемый естественный или стандартный базис (о
базисе ниже) из трех (единичных) векторов
В этом случае вектор
Слайд 13Векторы
представим в виде
Эти две записи (правая и левая) можно
рассматривать как эквивалентные. Говорят, что вектор х разложим по векторам
еi. Разложение вектора по базису единственно. Концепция разложения векторов на составляющие весьма полезна.Слайд 14Линейная зависимость векторов
Множество векторов {an} называется линейно зависимым,
если существуют коэффициенты {kn} не все равные нулю, что
линейная комбинация равна нулюk1a1 + k2a2 + k3a3=0.
Другими словами, если линейная комбинация равна нулю, но хотя бы один коэффициент отличен от нуля, то вектора линейно зависимы.
Слайд 15Линейная зависимость векторов
Если векторы линейно зависимы, то по крайней
мере один из них линейно выражается через остальные. Подмножество векторов,
не являющееся линейно зависимым, называется линейно независимым. Любое подмножество линейно независимого множества также линейно независимо.Слайд 16Пример линейно зависимых векторов
Пример. Вектора на плоскости (-1; 4)
и (2; -8) линейно зависимы, т.к. их линейная( одна из
многих) комбинация равна нулю:-2⋅(-1; 4) - (2; -8)=0.
Слайд 17n-мерное векторное пространство . Базис
Совокупность n линейно независимых векторов
n-мерного векторного пространства V, порождающих это пространство, называется его базисом.
Существует много различных базисов. Однако все они обладают следующим свойством: любой элемент из нашего пространства V можно разложить по базису единственным способом.Слайд 18Единичным вектором является вектор, у которого длина равна единице (например,
у вектора лишь одна компонента равна единице, а остальные равны
нулю).Вектор можно записывать в виде столбца
Слайд 19Скалярное произведение векторов
Векторы можно перемножать. Допустим, что у нас имеется
два вектора
и ϕ обозначает угол между этими векторами. Тогда
число, полученное по формулеСлайд 20Скалярное произведение векторов
называют скалярным произведением векторов и обозначают также a⋅
b или 〈 a, b 〉. Скалярное произведение векторов является
скалярной величиной. Оно может быть вычислено простым умножением модуля вектора a на проекцию вектора b на a или перемножением соответствующих компонент векторов и сложением результатов (суммирование попарных произведений):Слайд 22Скалярное произведение векторов
Векторы a и b называются ортогональными, если их
скалярное произведение равно нулю a⋅ b = 0. Скалярное произведение
линейно.Скалярное произведение позволяет нам ОПРЕДЕЛИТЬ норму (длину) вектора:
Косинус угла ϕ между векторами равен:
Слайд 23Скалярное произведение векторов
Пример. Пусть заданы векторы р(a, b) и q(c,
d), тогда синус угла между ними может быть вычислен по
формуле:где Δ - определитель, составленный из координат векторов (см. следующий слайд)
Слайд 25Площадь параллелограмма
Утверждение. Пусть ABCD произвольный параллелограмм, заданный векторами р(a, b)
и q(c, d). Тогда площадь S параллелограмма равна Δ.
В
самом деле:Замечание. Площадь треугольника равна1/2Δ
Слайд 26Равенство нулю определителя
Определитель треугольной матрицы равен произведению диагональных элементов.
Слайд 27Определитель треугольной матрицы
Например.
Рассмотрим пример нахождения определителя. Мы можем к
любой строке прибавить строку. Воспользуемся этим для преобразования определителя к
Слайд 29Значение этого определителя не надо искать, т.к. его величина равна
нулю(!).Третий столбец пропорционален первому.
Слайд 30ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ
Матрица – это определенным образом представленное множество чисел.
Для удобства вычислений и обращения с ними, матрицы записываются в
виде таблицы. С математической точки зрения матрицы ведут себя как вектора (линейные объекты) и они образуют векторное пространство. Чтобы рассмотреть этот объект более подробно нужно обратиться к системе линейных алгебраических уравнений. Но сначала приведем основные положения.Слайд 31ОСНОВНЫЕ ПОНЯТИЯ
Матрица состоит из элементов – чисел.
Нулевой матрицей называется матрица,
у которой все элементы – нули. Квадратная матрица размера n
называется единичной, если все её элементы, стоящие на главной диагонали, равны единице, а все остальные – нули. Единичная матрица, как правило, обозначается буквой E или I:
Слайд 33 ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ
Основные понятия.
Рассмотрим систему m линейных алгебраических
уравнений с n неизвестными:
Слайд 34
Решением системы называется упорядоченный набор из n чисел, обращающий каждое
уравнение системы в тождество.
Система, имеющая решение, называется совместной.
Если система имеет
только одно решение, то она называется определенной. Если система не имеет решений, то она называется несовместной.
Слайд 35Если число уравнений системы совпадает с числом неизвестных, то система
называется квадратной.
Преобразование, переводящее систему в новую систему, эквивалентную исходной, называется
элементарным.К элементарным преобразованиям относятся следующие преобразования:
перестановка местами двух уравнений системы,
перестановка местами (переобозначение)
Слайд 36 двух неизвестных с учетом их коэффициентов (симметрично у
всех уравнений),
умножение/деление обеих частей какого-либо уравнения системы на отличное
от нуля число, замена уравнения системы на сумму или разность этого уравнения с любым другим уравнением системы (прибавление к уравнению линейной комбинации других уравнений).
Слайд 37Если применить рассмотренные элементарные преобразования к матрице, то важнейшая ее
характеристика - ранг не будет меняться. Сама матрица при этом
изменит вид (подобно системе уравнений), но суть ее не изменится.Слайд 40 Далее мы будем основываться на системе (1) и рассмотрим
прямоугольную таблицу, состоящую из p строк и q столбцов, которую
мы назовем матрицей системы размера p×q:
Слайд 41
Можно сказать что,
матрица – это прямоугольная
таблица множества
чисел,
которые занумерованы
определенным порядком
(матрицу часто изображают жирным шрифтом)
Слайд 42Числа aij (i = 1,2, …, m; j =1, 2, …, n) называются элементами матрицы. Первый индекс фиксирует
номер строки, а второй – номер столбца, в которых стоит
данный элемент. Например, элемент а12 стоит в первой строке, во втором столбце. Множество всех p×q матриц обозначимМ p, q. Если число столбцов матрицы равно числу строк, то матрица называется квадратной (Мn). Элементы aii образуют главную диагональ матрицы, идущую из левого верхнего угла в правый нижний (например, а11, а22…).
Слайд 43Представленная матрица (2) называется матрицей коэффициентов системы линейных уравнений (1),
а матрица (3)–расширенной матрицей для исходной системы уравнений.
Для того, чтобы
получить расширенную матрицу, мы к матрице коэффициентов системы прибавляем (приписываем справа) столбец свободных элементов нашей системы (т.е. правые части). Число столбцов при этом увеличивается на единицу, а число строк остается тем же самым. Слайд 44На множестве матриц вводится понятие равенства. Две матрицы одинаковой размерности
p × q называются равными, если в них все элементы
с одинаковыми индексами равны. Приведем далее пример верхней треугольной матрицыСлайд 45На множестве согласованных (одинаковых) матриц вводится операция сложения, которая обозначается
символом «плюс» + и также, по аналогии с векторами, вводится
операция умножения матрицы на число («точка»), т.е. задается векторное пространство(Мp, q). Рассмотрим умножение на число.
Пусть A = (aij) – некоторая матрица и α – произвольный скаляр, т.е. действительное число.
Слайд 46Под произведением αA понимается матрица (αaij), то есть при умножении
матрицы A на число α все элементы матрицы A, умножаются
на это число.Сложение. Пусть A и B – матрицы одинаковой размерности:
A = (aij), B = (bij). Под суммой A + B понимается матрица C = (cij) той же размерности, каждый элемент которой определяется покомпонентным сложением по формуле: cij = aij + bij .
Слайд 48Операция сложения матриц коммутативна и ассоциативна (как для векторов).
На множестве
матриц вводится операция умножения одной матрицы на другую. Умножению матриц
отвечает композиции линейных отображений. Эта операция чем-то напоминает скалярное умножение векторов (х1⋅у1 + х2⋅у2 +х3⋅у3 ).Нейтральным элементом при умножении является единичная матрица.
Необходимо отметить следующее:
произведение определяется только для
Слайд 49тех матриц, для которых выполняется следующее условие:
матрицу A можно
умножить на матрицу B ( C = A × B),
если число столбцов матрицы A равно числу строк матрицы B.Каждый элемент получившейся матрицы C определяется по формуле:
Слайд 50т.е. элемент cij матрицы C равен сумме произведений элементов i-ой
строки первой матрицы- сомножителя на соответствующие элементы j-го столбца второй
матрицы-сомножителя (скалярное произведение строки и столбца).Из сказанного следует, что если можно найти произведение матриц AB, то произведение BA, вообще говоря, может не существовать( т.е умножение матриц не коммутативно). Но умножение матриц ассоциативно (АВ)С=А(ВС). Заметим, что умножение векторов – коммутативно.
Слайд 55Если произведения AB и BA одновременно определены, то, вообще говоря,
эти произведения могут быть не равны. Это означает, что умножение
матриц не коммутативно. Например,Слайд 56Мы получили в результате две неравные матрицы.
Если операция произведения матриц
выполнима, то выполняется условие дистрибутивности:
(А+В)С=АС+ВС
Общие правила алгебраических действий для матриц:
1)
A + B = B + A;Слайд 59Метод Гаусса решения систем линейных уравнений
Метод Гаусса – классический способ
решения системы линейных алгебраических уравнений путем последовательного исключения неизвестных и
преобразования системы уравнений к ступенчатому (треугольному) виду, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.Слайд 60Метод Гаусса решения систем линейных уравнений
Рассмотрим для примера систему двух
линейных уравнений с двумя неизвестными, которая имеет вид:
где
a, b, c, d, g, f – заданные числа; x, y – неизвестные. Числа a, b, c, d – коэффициенты при неизвестных; f, g – свободные члены. Слайд 61Метод Гаусса решения систем линейных уравнений
Решение этой системы уравнений может
быть найдено основными методами подстановки и сложения или же Крамера.
1.
Метод подстановки. Из одного уравнения выражаем неизвестное, например x, через коэффициенты
Слайд 62Метод подстановки
и другое неизвестное - y (предполагаем а≠0):
x
= ( f – by ) / a
Подставляем во второе уравнение вместо x :
c·( f – by ) / a + dy = g.
Находим у и т.д.
2.Сложение или вычитание.
Этот метод можно проиллюстрировать так.
Слайд 63Метод сложения
Рассмотрим пример. Из одного уравнения вычитаем/складываем другое (это
элементарное преобразование), например
Слайд 64Метод Гаусса решения систем линейных уравнений
Идея состоит в исключении переменных.
С
точки зрения линейной алгебры этот метод соответствует разложению матрицы коэффициентов
в произведение A=NU нижней треугольной N и верхней треугольной матрицы U.С точки зрения вычислительной математики число арифметических операций при этом пропорционально n3/3.
Слайд 65Метод Гаусса решения систем линейных уравнений
При решении систем чаще всего
число уравнений совпадает с числом неизвестных (например, линейная модель экономики
В. Леонтьева или статистические регрессивные модели). В этих случаях удается найти единственное решение задачи. Если число неизвестных больше числа уравнений, например, в задачах линейного программирования, то может существовать бесконечное число решений. Может встретиться система, где число уравнений больше числа неизвестных. Однако может оказаться, что не все эти уравненияСлайд 66Метод Гаусса решения систем линейных уравнений
являются независимыми, а некоторые
могут представлять линейную комбинацию других.
В этом случае желательно найти достаточное
количество независимых уравнений, чтобы получить решение.На основе рассмотренного примера при решении произвольных систем возникает желание найти процедуру, например, процедуру последовательного исключения неизвестных и нахождения величин x1, x2,…, xn, которые удовлетворяют всем нашим уравнениям. Рассмотрим пример.
Слайд 67 Метод Гаусса решения систем линейных уравнений
Предположим, что нам надо решить
систему линейных уравнений, например:
Слайд 68метод
1. Устанавливается строка, с помощью которой будем производить исключение и
находим ведущий элемент (стрелка);
2. Проводим с помощью элементарных преобразований исключение
переменной х1 из всех уравнений (кроме первого);3. Аналогично исключаем х2, х3 ,… хn-1 , пока не останется одно уравнение;
4. Система решается снизу вверх путем подстановки найденных решений в соответствующие уравнения.
Слайд 69 В первом уравнении ведущий или разрешающий коэффициент(со стрелочкой) равен
двум (не равен нулю). Мы используем первое уравнение для исключения
х1. Делим это уравнение на два и три раза отнимаем его из второго уравнения, получаем:
Слайд 70Первое уравнение у нас остается без изменения. Для дальнейшего исключения
х1 просто вычитаем модифицированное первое уравнение из третьего и получаем:
Слайд 71Используя второе уравнение из новой системы, исключаем х2 в третьем
уравнении. Для этого мы можем второе уравнение умножить на пять
и вычесть из третьегоСлайд 73Из третьего уравнения находим х3 =3. Подставляя это значение в
первые два уравнения, находим остальные неизвестные
Слайд 74Окончательно находим решение системы х1 =1, х2 =2, х3 =3.
Модифицированный
метод (Гаусса-Жордана) предполагает, что первый (и второй) шаг являются таким
же как в методе Гаусса и мы получаем систему (5). Далее, используя второе уравнение получаем х2 и результат подставляем и в первое и в третье уравнения. Об этом см. далее. Если в результате преобразований все коэффициенты при неизвестных в какой-нибудь строке окажутся равнымиСлайд 75нулю, а правая часть не будет равна нулю, то данная
система несовместна.
Метод Жордана-Гаусса
Решить систему уравнений:
Слайд 76Запишем матрицу и приведем ее к разрешенному виду за пять
шагов (ведущий элемент отмечаем штрихом). Из первой и третьей строк
вычитаем вторую:Слайд 81В результате исходная система принимает следующий вид:
В итоге имеем решение:
х1 =-2; х2 =2;
х3 =1.
Слайд 82 Метод Гаусса решения систем линейных уравнений
Рассмотрим квадратную систему линейных уравнений,
например:
Слайд 83Для того, чтобы избавиться от х1 мы должны определиться с
коэффициентом a11 (ведущий элемент) и убедиться, что он отличен от
нуля. Если это не так, то нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.1) поскольку в нашем случае a11≠0, первое уравнение оставим без изменений;
Слайд 842) наша задача исключить x1 из второго и т.д. уравнений; исключим
x1 во втором уравнении системы: для этого вычтем из второго
уравнения системы первое уравнение, умноженное на 4;3) аналогично исключим x1 в третьем уравнении системы: для этого вычтем из третьего уравнения системы первое уравнение, умноженное на 3;
4) исключим x1 в четвертом уравнении системы: для этого вычтем из четвертого уравнения системы первое уравнение, умноженное на 5. Переменные можно не рассматривать.
Слайд 85 Продолжим. Преобразуем полученную матрицу следующим образом:
1) первые две строки оставим
без изменения, поскольку элемент a22 не равен нулю (=10);
Слайд 862) вместо третьей строки запишем разность между второй строкой и удвоенной
третьей; мы можем так поступать.
3) четвертую строку заменим разностью между удвоенной
второй строкой и умноженной на 5 четвертой.В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
Слайд 87Теперь исключим неизвестную x3 из четвертого уравнения. Для этого полученную
матрицу преобразуем так:
1) первые три строки оставим без изменения, так как
a33 ≠ 0;2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:
Слайд 89Очевидно, мы получили треугольную систему.
Отсюда находим : x4 = 2.
Подставив это значение в третье уравнение, получим x3 = 3.
Теперь из второго уравнения следует, что x2 = 1, а из первого, что x1 = –1. Очевидно, что полученное решение единственно (возможна проверка).Слайд 90То есть наша матрица представляет собой в общем случае ступенчатую
матрицу, которую получили преобразованием (Гаусса). Но может быть это случайно?
На самом деле любая матрица посредством серии элементарных преобразований может быть приведена к ступенчатой.Слайд 91Транспонирование матрицы.
При транспонировании матрицы строки и столбцы меняются местами. Операция
транспонирования обозначается звездочкой или индексом Т.
Слайд 93ОБРАТНАЯ МАТРИЦА
Обратная матрица вводится по аналогии с алгебраическим соотношением а
⋅ а -1=1.
Пусть A – квадратная матрица. Обратной матрицей
к матрице A называется такая матрица A–1, для которой справедливы равенства:А ⋅A–1 = A–1 ⋅A = E.
Таким образом, произведение матрицы на обратную равно единичной матрице.
Слайд 94Заметим, что не всякая квадратная матрица имеет обратную матрицу.
Теорема.
Для того,
чтобы матрица А имела обратную, необходимо и достаточно, чтобы она
была невырожденной (т.е. определитель не равен нулю или все строки – линейно независимы).Для того, чтобы найти обратную матрицу к матрице второго порядка 2х2:
Слайд 96По этой формуле, если разность ad-bc не равна нулю (т.е.
матрица А не вырождена) обратная матрица получается из исходной заменой
местами чисел a и d относительно боковой диагонали, при одновременном изменении знака у b и c на противоположный. Вновь полученная матрица умножается на коэффициент(ad-bc)-1 .
Например:
Слайд 98Свойства обратной матрицы
Е-1 =Е;
(А-1) -1 =А.
Для получения обратной матрицы достаточно
к строкам единичной матрицы применить те преобразования, которые приводят матрицу
А к единичной (метод Жордана-Гаусса).Слайд 100 ТЕОРИЯ
ОПРЕДЕЛИТЕЛЕЙ
Основные понятия.
Часто в математике желательно охарактеризовать объект, определяемый многими
параметрами, с помощью одной величины. Пример такого рода – определитель. Определитель является инвариантом.
Слайд 101Определение детерминанта det
Квадратной матрице А (порядка n) ставится в соответствие
число, называемое определителем или детерминантом (det), вычисляемое на основе значений
ее элементов. Определитель равен алгебраической сумме всевозможных произведений его элементов, по одному из каждой строки и каждого столбца. Слагаемые называются членами определителя.Слайд 102Определение детерминанта det
Каждый член определителя равен произведению n элементов матрицы
А. Число всех членов определителя n -го порядка равно n!.
Слайд 103Свойства определителя
Определитель не меняется при транспонировании матрицы.
Определитель равен нулю тогда
и только тогда, когда строки (столбцы) матрицы линейно зависимы. Такая
матрица называется вырожденной.Если любую строку матрицы умножить на число, то и определитель матрицы умножится на это число.
Слайд 104Свойства определителя
Определитель меняет знак, если две строки поменять местами.
!!! Определитель
не меняется, если к какой-либо строке матрицы прибавить любую линейную
комбинацию остальных строк.Если элементы строки матрицы представлены в виде суммы aij= bij+cij, то определитель равен сумме двух определителей, у которых все строки,
Слайд 105 кроме i–ой такие же, а i–я строка в
одном из них содержит элемент bij, а в другом -
cij.Определитель треугольной матрицы равен произведению диагональных элементов.
Теорема. Определитель произведения квадратных матриц равен произведению определителей матриц-сомножителей.
Слайд 108Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными
Эту
систему решаем с помощью определителей. Для этого нам нужно найти
определитель третьего порядка.
Слайд 109Определителем произвольной квадратной матрицы третьего порядка
называется сумма шести слагаемых, каждое
из которых представляет собой произведение трех элементов матрицы, выбираемых
Слайд 110по следующему правилу: три произведения элементов, стоящих на главной диагонали
и в вершинах двух треугольников с основаниями, параллельными главной диагонали
берутся
со знаком "+", а три произведения элементов, стоящих на побочной диагонали и в вершинах двух других треугольников