Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические основы цифровых устройств
Содержание
- 1. Логические основы цифровых устройств
- 2. Аналоговая – непрерывная(воспринимается человеком)Дискретная – скачкообразная(воспринимается вычислительной
- 3. Кодирование информацииКодирование - формирование представления информации с помощью некоторого
- 4. Шифрование сообщенияШифрование - процесс превращения открытого текста
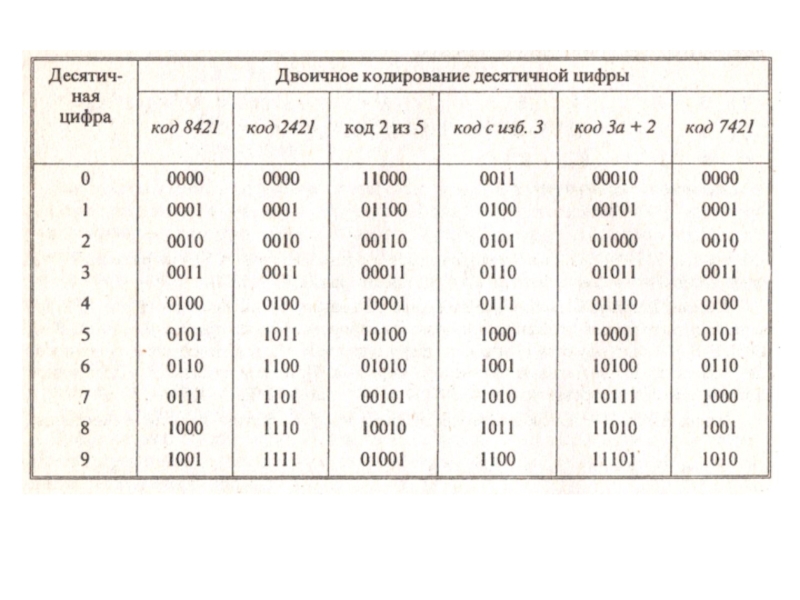
- 5. Коды, применяемые в ЭВМНеравномерные коды
- 6. Оптический телеграф ШаппаСистема Шаппа позволяла передавать сообщения на скорости два слова в минуту
- 7. Шрифт БрайляСпециальный шрифт для слепыхБуквы этого шрифта
- 8. Первый телеграфкодирование сводится к использованию набора символов,
- 9. Первый беспроводной телеграф (радиоприемник)7 мая 1895 года
- 10. Коды, применяемые в ЭВМРавномерные коды
- 11. Телеграфный аппарат БодоИспользовалось всего два разных вида
- 12. Представление информации в ЭВМ
- 13. Информацию, представленную различными устойчивыми состояниями некоторого физического
- 14. Большие объемы информации измеряются с помощью производных
- 15. Формы представления чисел в ЭВМДля эффективности использования
- 16. Двоичное кодированиеВся информация, которую обрабатывает компьютер должна
- 17. Почему двоичное кодирование?0 – отсутствие электрического сигнала;1 – наличие электрического сигнала.Передача электрических сигналов:
- 18. Плюсы двоичного кодированияв такой форме можно закодировать
- 19. Количество информации. Формула ХартлиI=log2N; N=2Iгде I —
- 20. 2. Системы счисления
- 21. Основные понятияСистема счисления — это совокупность приемов
- 22. Системы счисления (СС)Непозиционные (кодовые)Позиционныеколичественный эквивалент значения каждого
- 23. Основные достоинства любой позиционной системы счисленияпростота выполнения
- 24. Представление чисел в позиционных системах счисления
- 25. Базисом позиционной системы счисления называется последовательность чисел,
- 26. Развернутая и свернутая формы записи числаЛюбое вещественное
- 27. Развернутая форма записиAq = (an–1qn–1 + an–2qn–2
- 28. Слайд 28
- 29. Преобразование чисел из одной системы счисления в другую
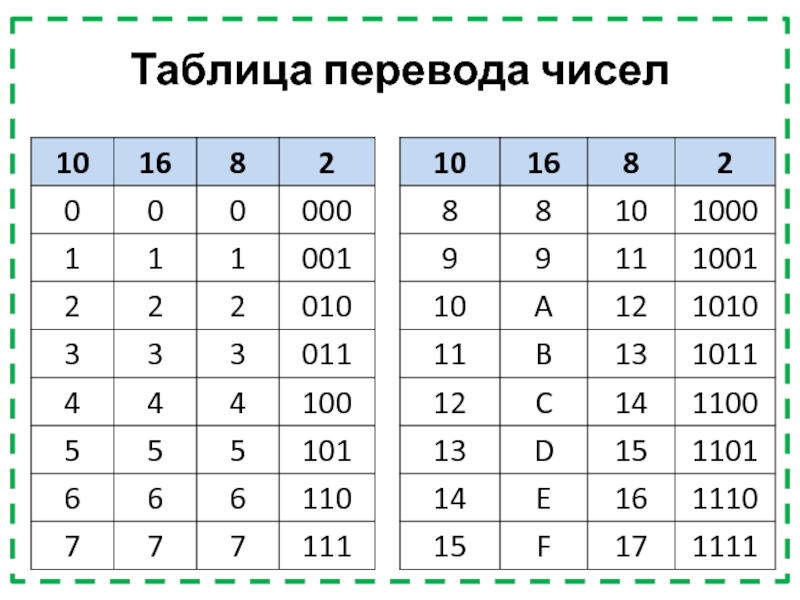
- 30. Таблица перевода чисел
- 31. Для перевода целого десятичного числа производится деление
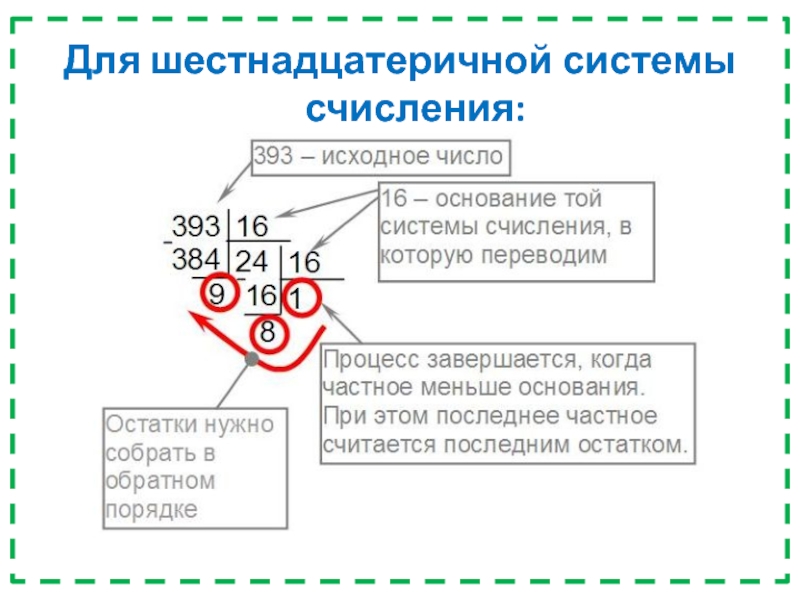
- 32. Для шестнадцатеричной системы счисления:
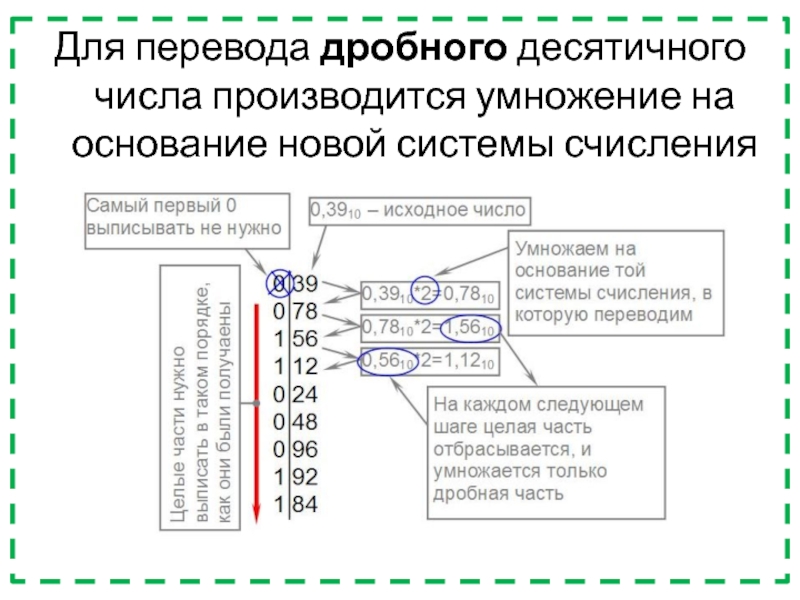
- 33. Для перевода дробного десятичного числа производится умножение на основание новой системы счисления
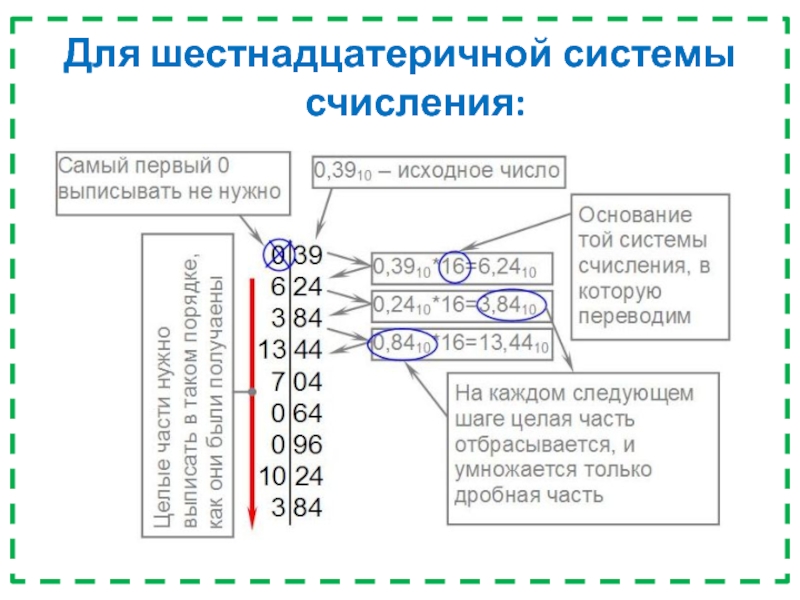
- 34. Для шестнадцатеричной системы счисления:
- 35. Перевод небольших целых чисел из десятичной системы счисления в двоичнуюЧисло 5Число 10
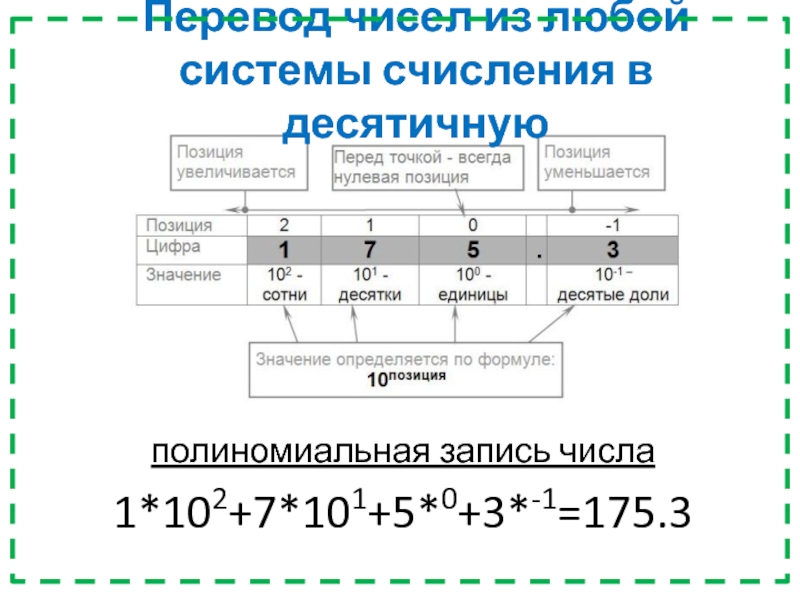
- 36. Перевод чисел из любой системы счисления в десятичнуюполиномиальная запись числа1*102+7*101+5*0+3*-1=175.3
- 37. Перевод небольших целых чисел из двоичной системы
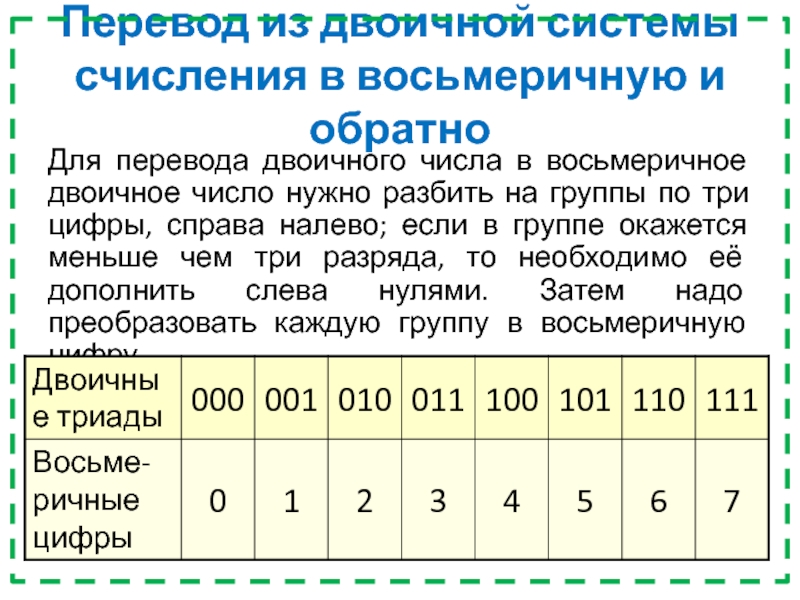
- 38. Перевод из двоичной системы счисления в восьмеричную
- 39. Перевод из двоичной системы счисления в шестнадцатеричную
- 40. 3. Двоичная арифметика
- 41. СложениеПравила сложения:0 + 0 = 01 +
- 42. ВычитаниеПравила вычитания:0 - 0 = 01 -
- 43. Алгебраическое сложение с использованием дополнительного кодаСложение уменьшаемого
- 44. УмножениеПравила умножения:0 · 0 = 01 ·
- 45. ДелениеДеление в двоичной системе счисления выполняется, как
- 46. Скачать презентанцию
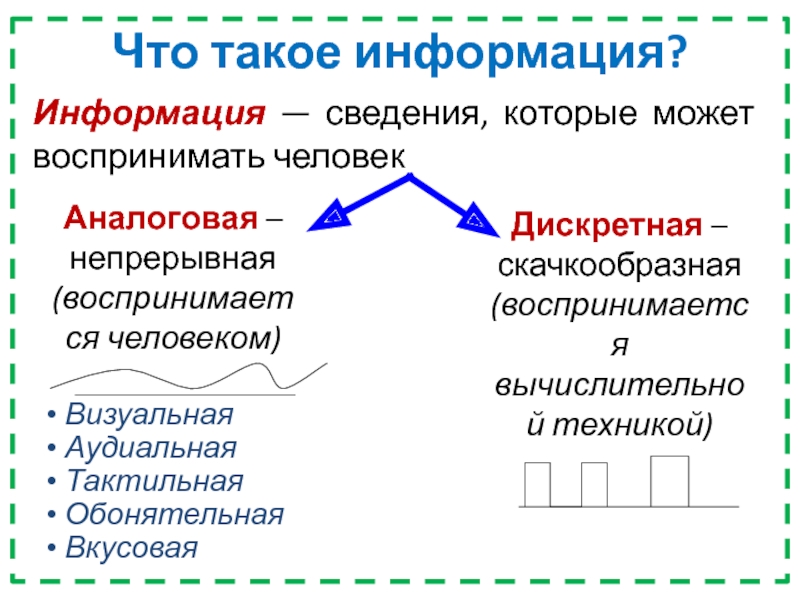
Аналоговая – непрерывная(воспринимается человеком)Дискретная – скачкообразная(воспринимается вычислительной техникой)Что такое информация?Информация — сведения, которые может воспринимать человек Визуальная Аудиальная Тактильная Обонятельная Вкусовая
Слайды и текст этой презентации
Слайд 2Аналоговая – непрерывная
(воспринимается человеком)
Дискретная – скачкообразная
(воспринимается вычислительной техникой)
Что такое информация?
Информация
— сведения, которые может воспринимать человек
ВкусоваяСлайд 3Кодирование информации
Кодирование - формирование представления информации с помощью некоторого кода (или можно
сказать, что кодирование, это переход от одной формы представления информации
к другой, более удобной для хранения, передачи или обработки).Декодирование - это процесс восстановления содержания закодированной информации.
Все множество символов, используемых для кодирования, называется алфавитом кодирования.
Слайд 4Шифрование сообщения
Шифрование - процесс превращения открытого текста в зашифрованный, а
дешифрование —процесс обратного преобразования, при котором восстанавливается исходный текст.
Методами
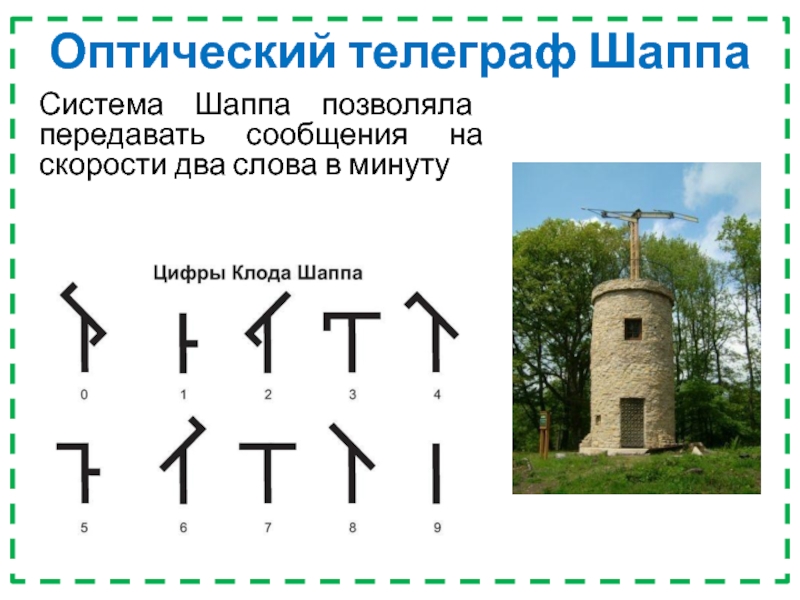
шифрования занимается наука под названием криптография.Слайд 6Оптический телеграф Шаппа
Система Шаппа позволяла передавать сообщения на скорости два
слова в минуту
Слайд 7Шрифт Брайля
Специальный шрифт для слепых
Буквы этого шрифта выдавливались на листках
плотной бумаги. Проводя пальцами по образовавшимся от уколов выступам, люди
учатся различать буквы и могут читать специальные книги.Слайд 8Первый телеграф
кодирование сводится к использованию набора символов, расположенных в строго
определенном порядке.
Самым знаменитым телеграфным сообщением является сигнал бедствия "SOS" (Save
Our Souls - спасите наши души)Слайд 9Первый беспроводной телеграф (радиоприемник)
7 мая 1895 года российский ученый
А. С. Попов продемонстрировал прибор, названный им "грозоотметчик", который
был предназначен для регистрации электромагнитных волн.Этот прибор считается первым в мире аппаратом беспроводной телеграфии - радиоприемником
Слайд 11Телеграфный аппарат Бодо
Использовалось всего два разных вида сигналов
Длина кода
всех символов одинаковая и равна пяти
Код Бодо — это первый
в истории техники способ двоичного кодирования, информации. Слайд 13Информацию, представленную различными устойчивыми состояниями некоторого физического носителя в форме,
воспринимаемой и обрабатываемой компьютером или человеком, называют данными.
Информацию о последовательности
операций, которые необходимо осуществить для получения по исходным данным требуемого результата, называют программой.Слайд 14Большие объемы информации измеряются с помощью производных единиц: килобайт, мегабайт
и гигабайт.
1 Кбайт = 210 байт = 1024 байт;
1
Мбайт = 220 байт = 1024 Кбайт;1 Гбайт = 230 бaйт = 1024 Мбайт.
Слайд 15Формы представления чисел в ЭВМ
Для эффективности использования памяти в ЭВМ
используют разные методы представления целых чисел.
С фиксированной запятой;
С плавающей
запятой. Слайд 16Двоичное кодирование
Вся информация, которую обрабатывает компьютер должна быть представлена двоичным
кодом с помощью двух цифр: 0
и 1.Двоичное кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
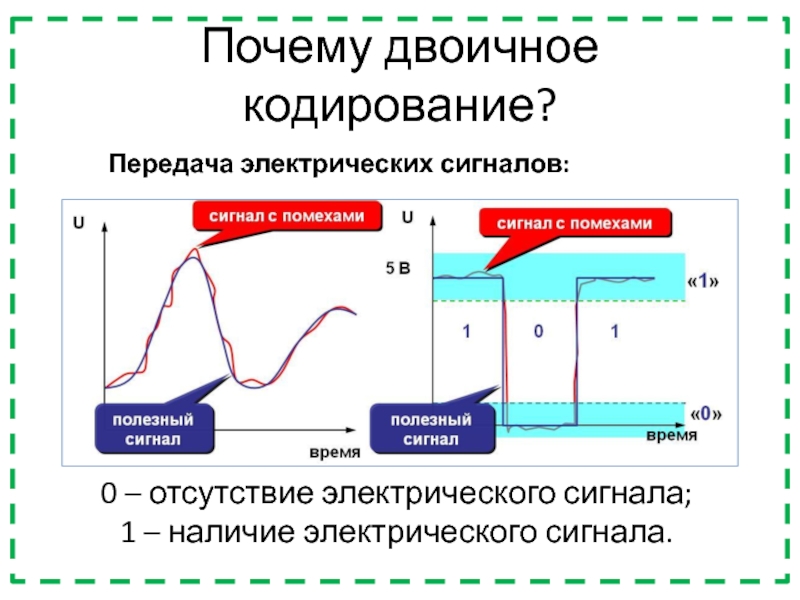
Слайд 17Почему двоичное кодирование?
0 – отсутствие электрического сигнала;
1 – наличие электрического
сигнала.
Передача электрических сигналов:
Слайд 18Плюсы двоичного кодирования
в такой форме можно закодировать все виды информации
нужны
только устройства с двумя состояниями
практически нет ошибок при передаче
компьютеру легче
обрабатывать данныеМинус двоичного кодирования
человеку сложно воспринимать двоичные коды
Слайд 19Количество информации. Формула Хартли
I=log2N; N=2I
где I — количество информации, несущей
представление о состоянии, в котором находится объект (несет в себе
один из вариантов);N — количество равновероятных альтернативных состояний (вариантов или чисел) объекта.
Слайд 21Основные понятия
Система счисления — это совокупность приемов и правил для
обозначения и наименования чисел.
Алфавит системы счисления — это множество всех
символов (знаков), используемых для записи чисел в данной системе счисления.Цифра — это любой символ (знак), входящий в алфавит данной системы счисления.
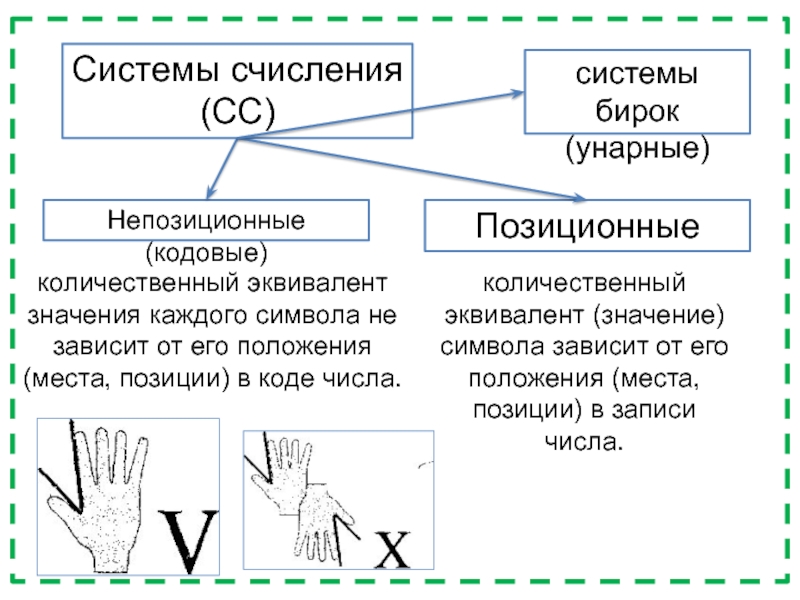
Слайд 22Системы счисления (СС)
Непозиционные (кодовые)
Позиционные
количественный эквивалент значения каждого символа не зависит
от его положения (места, позиции) в коде числа.
количественный эквивалент (значение)
символа зависит от его положения (места, позиции) в записи числа.системы бирок (унарные)
Слайд 23Основные достоинства любой позиционной системы счисления
простота выполнения арифметических операций
ограниченное
количество символов, необходимых для записи любых чисел
Слайд 25Базисом позиционной системы счисления называется последовательность чисел, каждое из которых
определяет количественный эквивалент (вес) символа в зависимости от его места
в коде числа.Базис десятичной системы счисления:
…10n, 10n–1,…, 101, 100, 10–1, …, 10–m ,…
Базис произвольной позиционной системы счисления:
…qn, qn–1, …, q1, q0, q–1, …, q–m, …
Основанием позиционной системы счисления называется целое число q, которое возводится в степень.
Слайд 26Развернутая и свернутая формы записи числа
Любое вещественное число может быть
представлено в следующем виде:
...a2 a1 a0, a-1 a-2 ...
Здесь
a0 , a1 – обозначают цифры нулевого, первого и т.д. разрядов целой части числа, a-1 a-2 – цифры первого, второго и т.д. разрядов дробной части числа.
Слайд 27Развернутая форма записи
Aq = (an–1qn–1 + an–2qn–2 +…+ a0q0 +…+a–1q–1
+ a–2q–2 +…+ a–mq–m),
А — само число;
q — основание
системы счисления; аi — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
т — количество дробных разрядов числа.
Разряд – позиция, которая занимает определенную цифру в положении числа
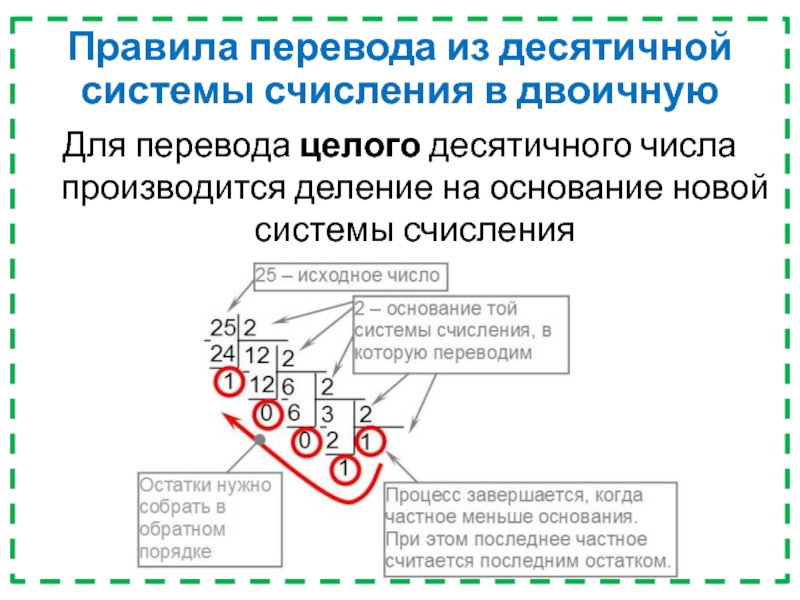
Слайд 31Для перевода целого десятичного числа производится деление на основание новой
системы счисления
Правила перевода из десятичной системы счисления в двоичную
Слайд 33Для перевода дробного десятичного числа производится умножение на основание новой
системы счисления
Слайд 36Перевод чисел из любой системы счисления в десятичную
полиномиальная запись числа
1*102+7*101+5*0+3*-1=175.3
Слайд 37Перевод небольших целых чисел из двоичной системы счисления в десятичную
число
10112
это сумма чисел 8+2+1=11
число 01102
это сумма чисел
4+2=6
Слайд 38Перевод из двоичной системы счисления в восьмеричную и обратно
Для перевода
двоичного числа в восьмеричное двоичное число нужно разбить на группы
по три цифры, справа налево; если в группе окажется меньше чем три разряда, то необходимо её дополнить слева нулями. Затем надо преобразовать каждую группу в восьмеричную цифру.Слайд 39Перевод из двоичной системы счисления в шестнадцатеричную и обратно
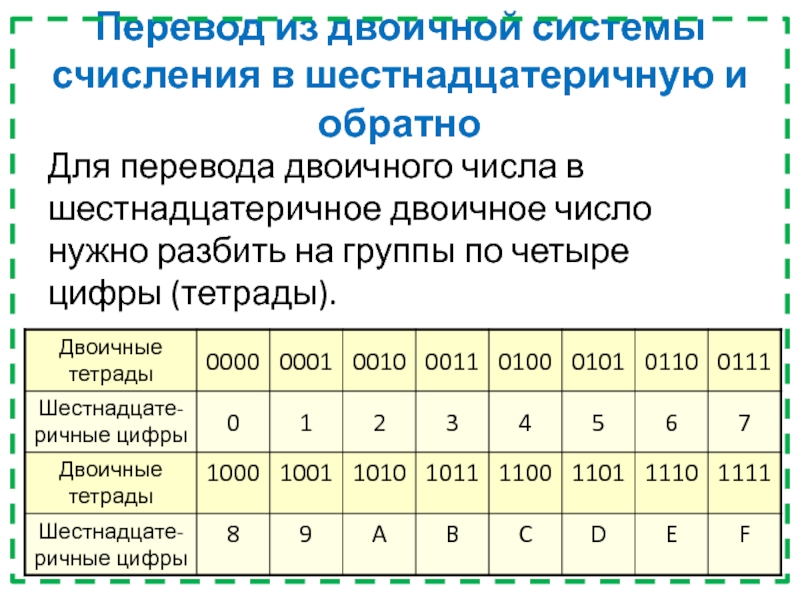
Для перевода
двоичного числа в шестнадцатеричное двоичное число нужно разбить на группы
по четыре цифры (тетрады).Слайд 41Сложение
Правила сложения:
0 + 0 = 0
1 + 0 = 1
0
+ 1 = 1
1 + 1 = (1)0
(результат сложения
двух единиц: ноль и единица переноса в старший разряд)Слайд 42Вычитание
Правила вычитания:
0 - 0 = 0
1 - 0 = 1
1
- 1 = 0
(1)0 - 1 = 1
(из нуля вычесть
единицу нельзя, поэтому для вычитания необходимо занять единицу у старшего разряда)Слайд 43Алгебраическое сложение с использованием дополнительного кода
Сложение уменьшаемого и дополнительного кода
вычитаемого с последующим отбрасыванием старшего разряда.
Дополнительный код:
Код положительного числа –
0Код отрицательного числа – 1
Слайд 45Деление
Деление в двоичной системе счисления выполняется, как и в десятичной
системе.
Пример:
10101 111
- 1 1 1 111 1 1
- 1 1 1
0