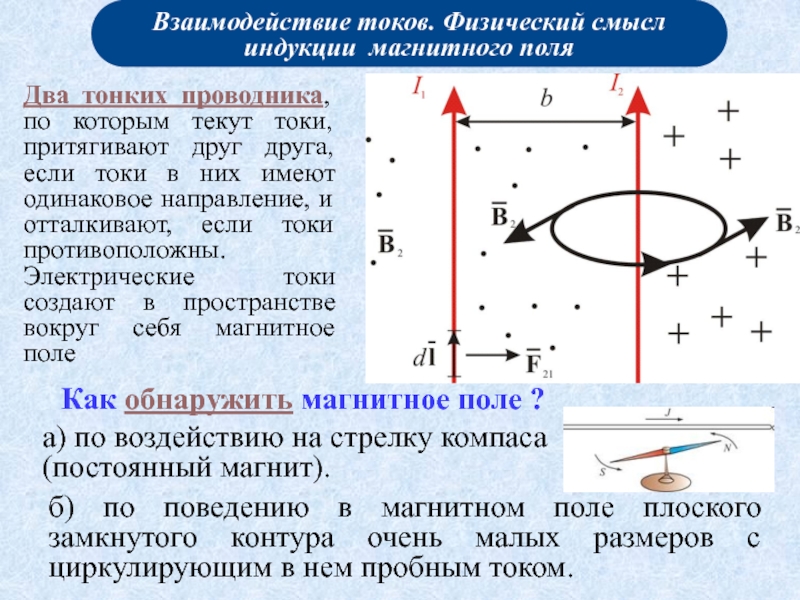
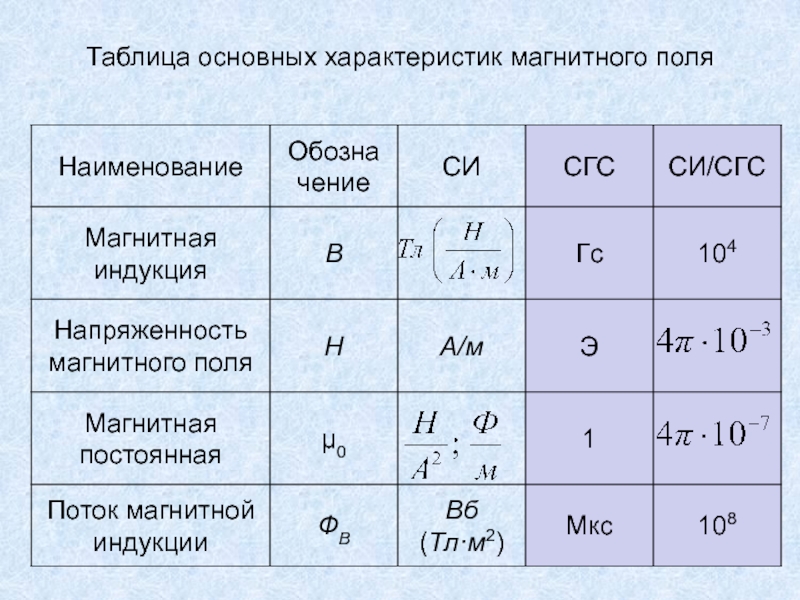
магнитного поля .
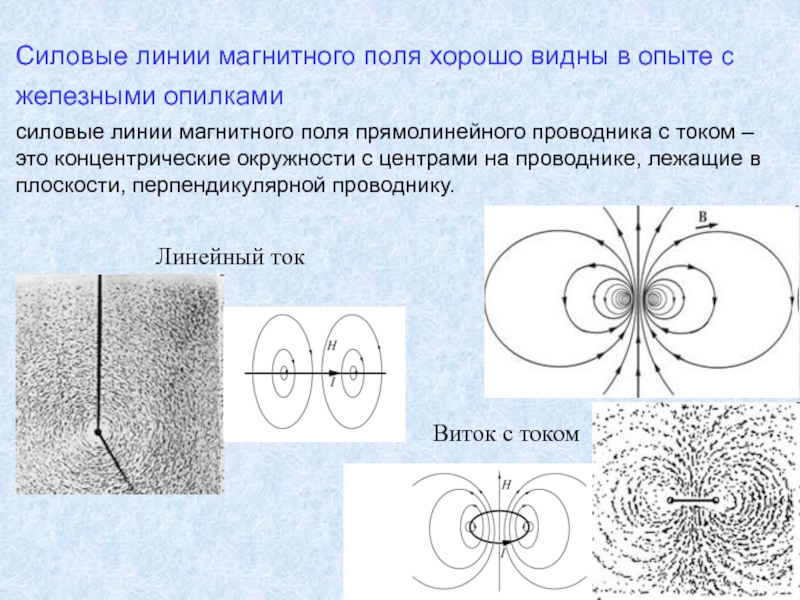
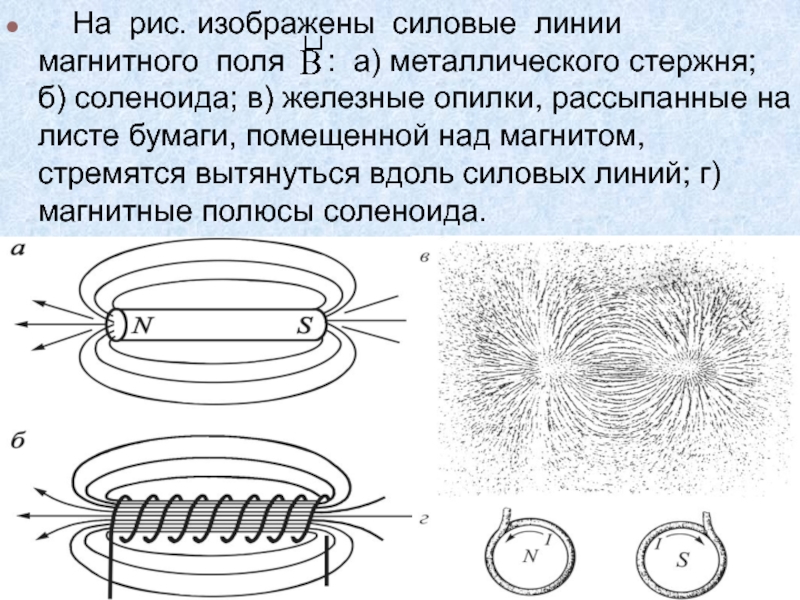
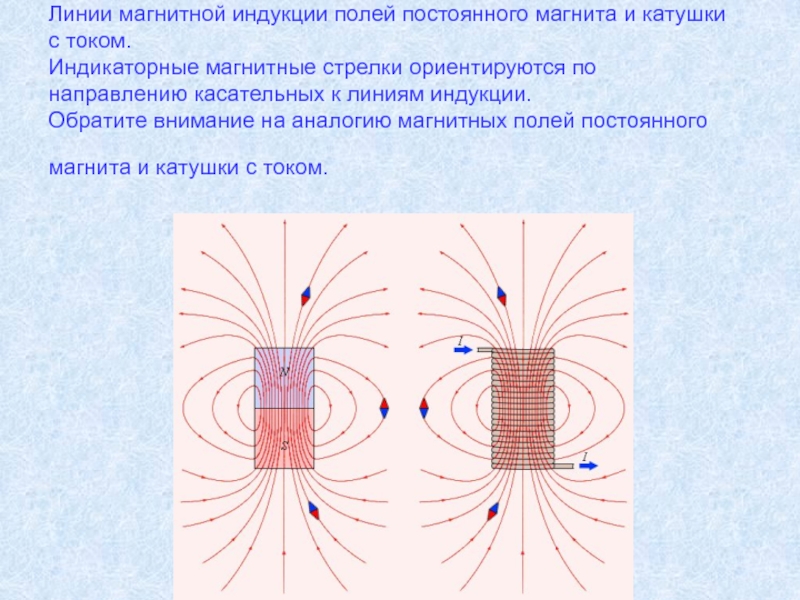
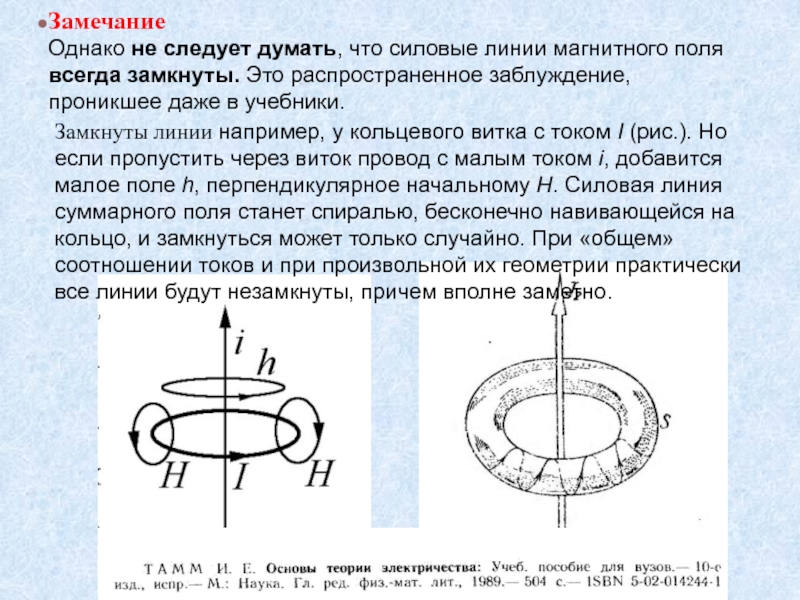
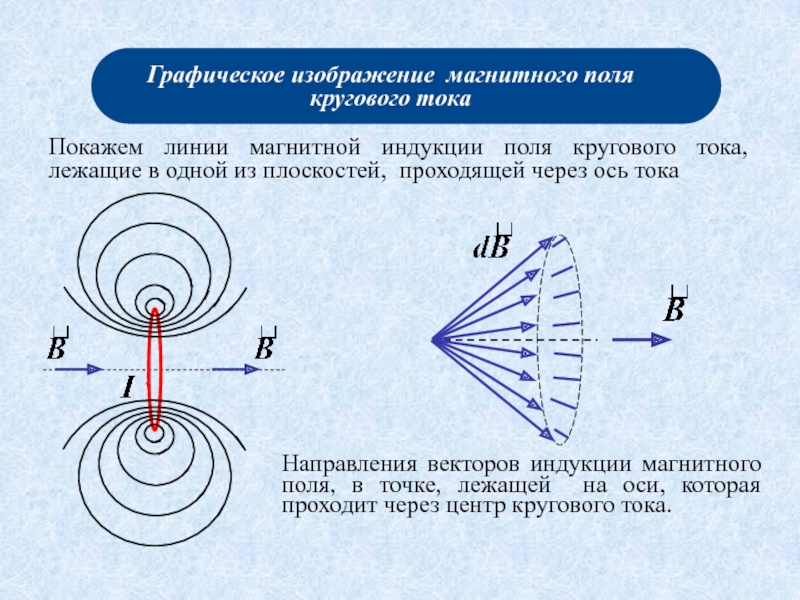
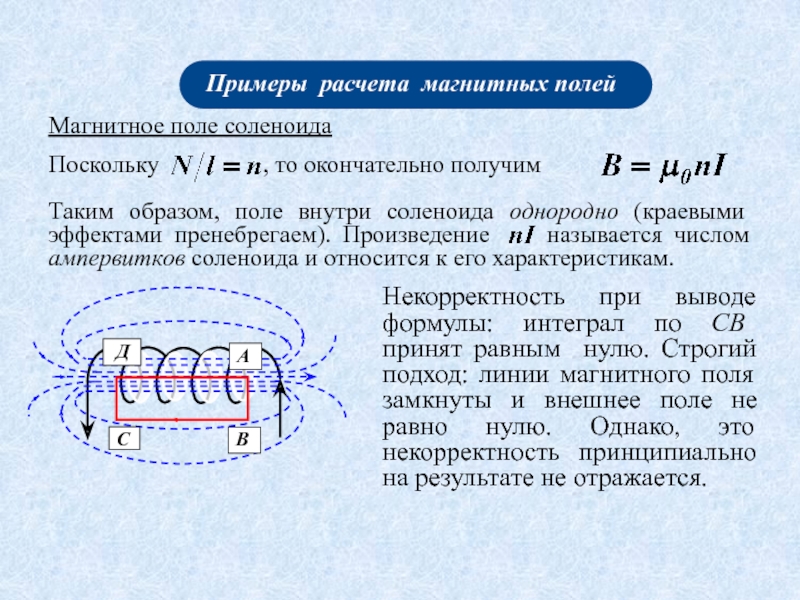
Графическое изображение магнитного поля.
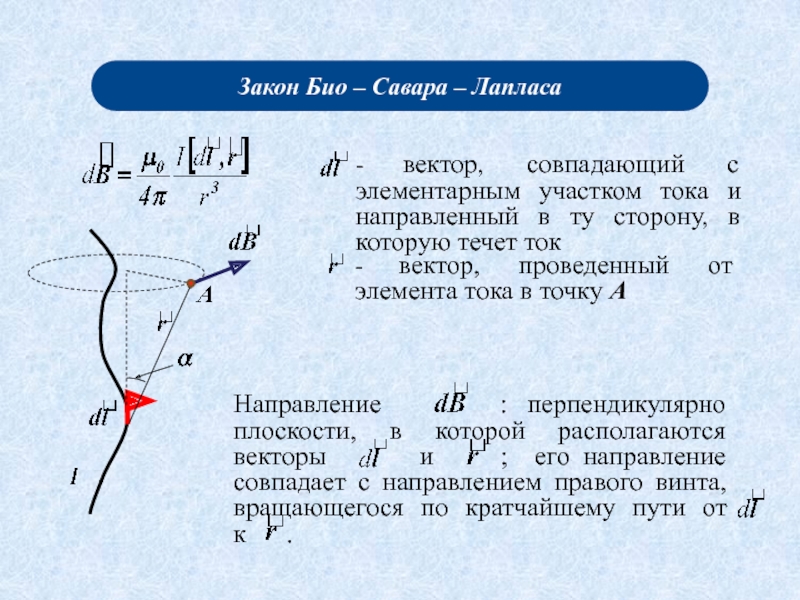
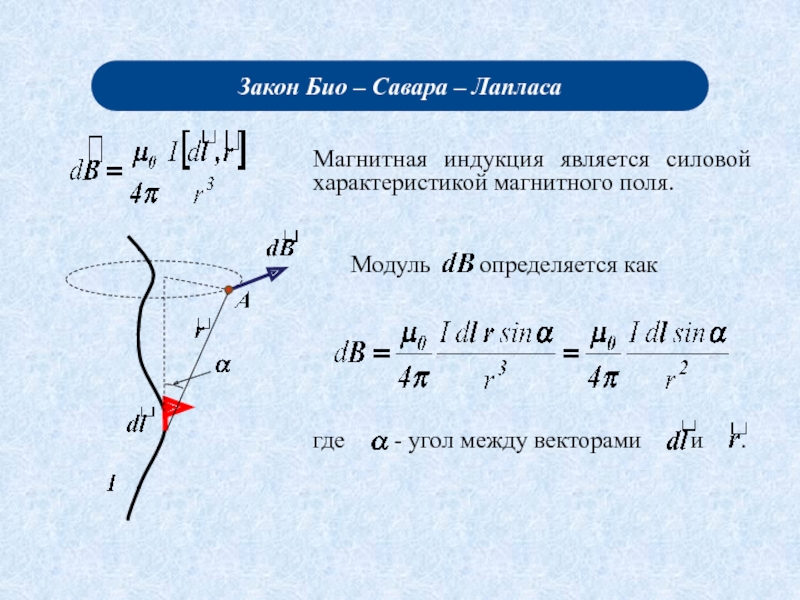
Закон Био – Савара
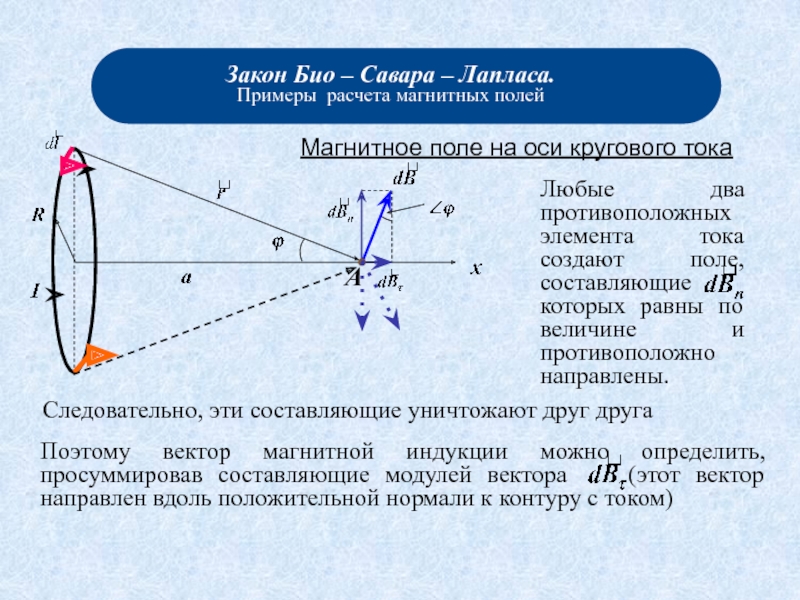
- Лапласа. Примеры расчета магнитных полей:
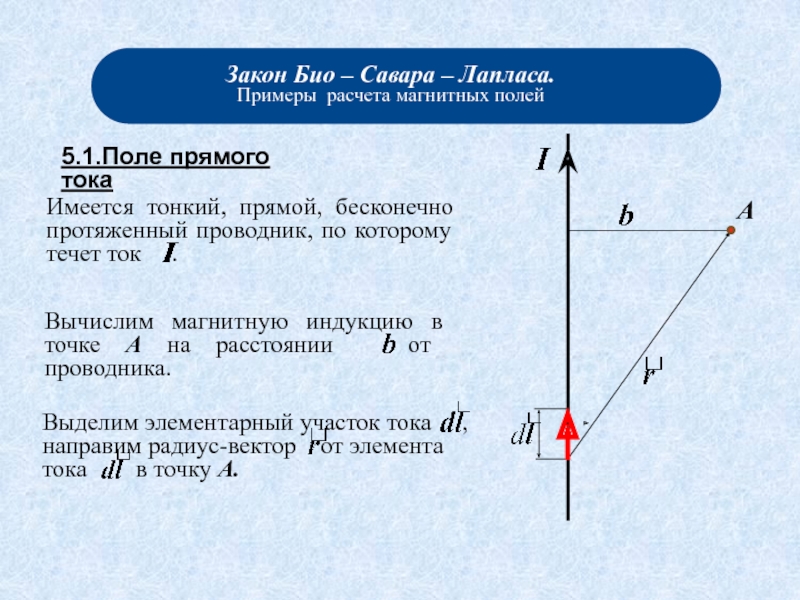
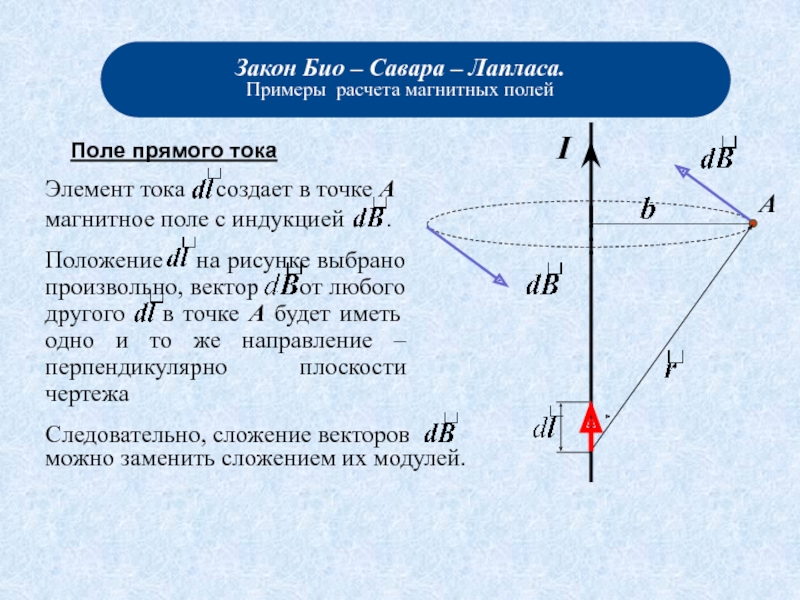
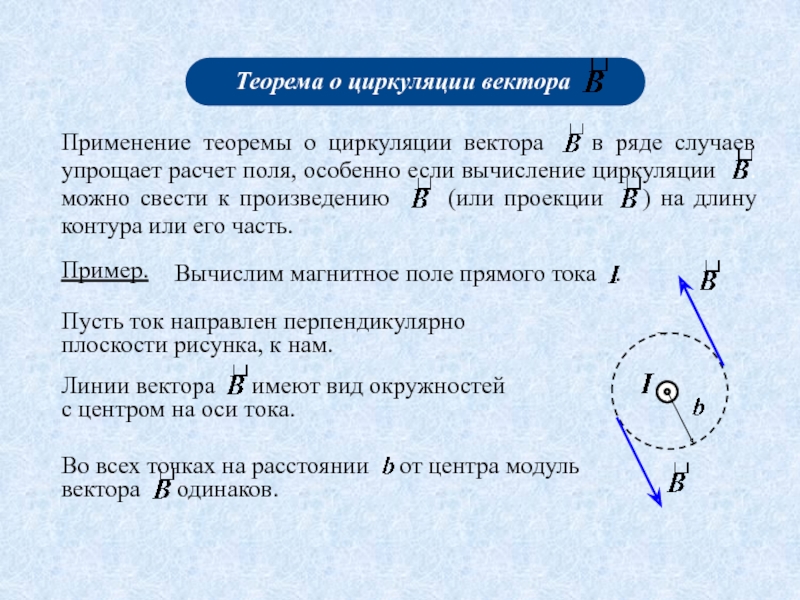
- 5.1.магнитное поле прямого тока;
- 5.2.магнитное поле равномерно движущегося заряда