Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический строй музыки
Содержание
- 1. Математический строй музыки
- 2. Так судьба стучится в дверьЛюдвиг ван БетховенСимфония № 5Людвиг ван Бетховен
- 3. Музыка - это радость души, которая вычисляет
- 4. Математика и музыка - два полюса человеческой
- 5. Известно открытие Пифагора в области теории музыки.
- 6. Для воплощения своего открытия Пифагор использовал монохорд
- 7. Архит 428 -365 до н.э.Архит родился в
- 8. 1.Частота колебания f звучащей струны обратно пропорциональна
- 9. Основой музыкальной шкалы - гаммы пифагорейцев был
- 10. Деление струны монохорда на части, образующие с
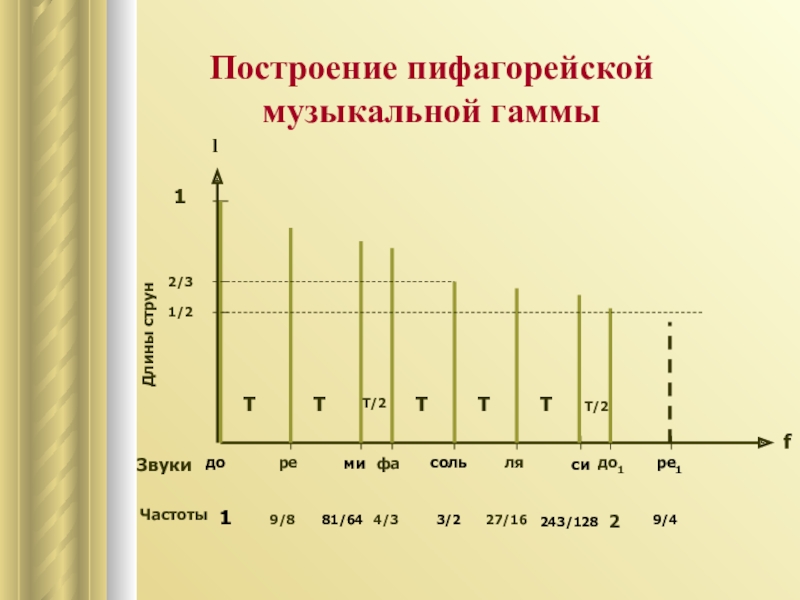
- 11. Построение пифагорейской музыкальной гаммыЗвукиЧастотыfДлины струн
- 12. Построение музыкальной гаммы обладает такой особенностью: двигаясь
- 13. На протяжении многих столетий музыканты настраивали инструменты
- 14. Пифагоров стройМУЗЫКАЛЬНЫЙ СТРОЙ, система отношений звуков по
- 15. Простой математический анализ многих музыкальных шедевров позволяет
- 16. Иоган Себастьян БахМы находим в произведениях Баха
- 17. Лунная сонатаЛюдвиг ван БетховенВ «Лунной сонате» проявление
- 18. Увертюра к опере
- 19. Итак, гармония космоса была воплощена пифагорейцами в
- 20. До сих пор никому не удавалось найти
- 21. Подготовить сообщение и презентацию по теме:«Что общего между Пифагором и Бахом?» Домашнее задание
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Музыка - это радость души, которая вычисляет , сама того
не замечая.
Г. Лейбниц
Раздумывая об искусстве и науке, об их взаимных
связях и противоречиях, я пришёл к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и что между ними размещается всё, что человечество создало в области науки и искусства.Генрих Нейгауз
Слайд 4Математика и музыка - два полюса человеческой культуры. Слушая музыку,
мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в
строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.Слайд 5Известно открытие Пифагора в области теории музыки. Необычность его в
том, что сочетание звуков, издаваемых струнами, наиболее благозвучно, если длины
струн музыкального инструмента находятся в правильном численном отношении друг к другу.Пифагор
«Музыка – величайшая сила. Она может заставить человека любить и ненавидеть, прощать и убивать».
Слайд 6Для воплощения своего открытия Пифагор использовал монохорд - полуинструмент, полуприбор.
Под струной на верхней крышке ученый начертил шкалу, с помощью
которой можно было делить струну на части. Было проделано много опытов, в результате которых Пифагор описал математически звучание натянутой струны.Монохорд
Слайд 7Архит
428 -365 до н.э.
Архит родился в г. Таренте, был учеником
пифагорейца Филолая, который сумел внушить ему интерес к научным проблемам
своей школы. Судьба Архита сложилась счастливо: он семь раз избирался стратегом, при этом, как полководец, не проиграл ни одного сражения. Но самое главное он был разносторонним учёным, механиком, математиком. Он много занимался арифметикой натуральных чисел, далеко продвинул теорию несоизмеримых величин. Архит считается самым крупным теоретиком музыки античности.Слайд 81.Частота колебания f звучащей струны обратно пропорциональна ее длине l.
f= a / l, (а - коэффициент, характеризующий физические свойства
струны).2. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n/(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
Эти интервалы – «совершенные консонансы», и их интервальные коэффициенты получили названия:
Октава l2/l1 =1/2 Квинта l2/l1 =2/3 Кварта l2/l1 =3/4
В основе музыкальной системы были два закона, которые носят имена двух великих ученых - Пифагора и Архита.
Слайд 9Основой музыкальной шкалы - гаммы пифагорейцев был интервал - октава.
Она является консонансом, повторяющим верхний звук. Для построения музыкальной гаммы
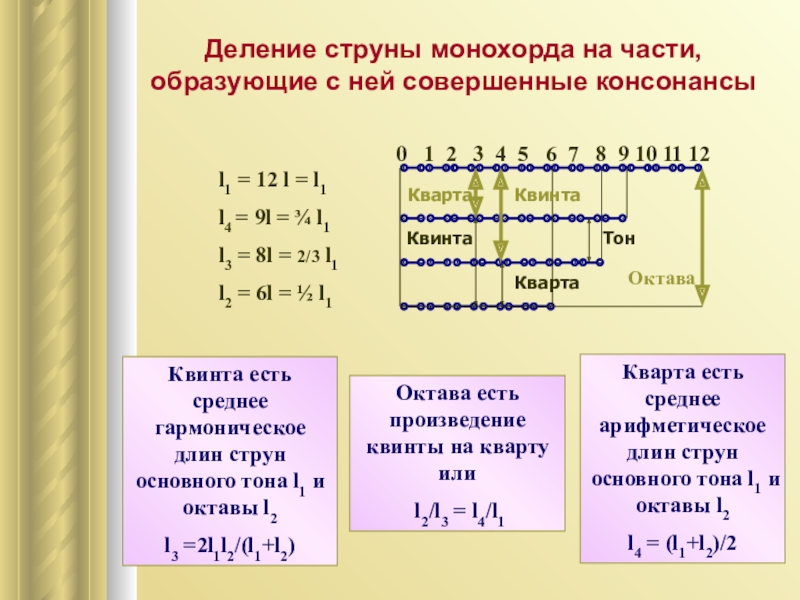
пифагорейцам требовалось разделить октаву на красиво звучащие части. Так как они верили в совершенные пропорции, то связали устройство гаммы со средними величинами: арифметическим, геометрическим, гармоническим.Слайд 10Деление струны монохорда на части, образующие с ней совершенные консонансы
Квинта
есть среднее гармоническое длин струн основного тона l1 и октавы
l2l3 =2l1l2/(l1+l2)
Кварта есть среднее арифметическое длин струн основного тона l1 и октавы l2
l4 = (l1+l2)/2
Октава есть произведение квинты на кварту или
l2/l3 = l4/l1
Слайд 12Построение музыкальной гаммы обладает такой особенностью: двигаясь по квинтам вверх
и вниз, не получится точного октавного повторения исходного звука. Лишь
12 квинт приближенно равны 7 октавам, а разделяющий их интервал называется пифагоровой коммой. Несмотря на свою малость, пифагорова комма на протяжении столетий "резала ухо" музыкантам. Взяв отношение (3/2)12:27, можно найти численное значение пифагоровой коммы (1,0136).Слайд 13На протяжении многих столетий музыканты настраивали инструменты так, как это
делали в Древней Греции. Однако этот настрой не мог казаться
им полностью подходящим, поскольку в нём сохранилась «пифагорова комма». Она была следствием несовершенства не только пифагорейской музыкальной гаммы, но и учения о числе. Теорию музыки оказалось возможным улучшить только после достаточного развития математики иррациональных величин.Но прежде, чем в науке утвердилось новое учение о числе , прежде, чем появился новый музыкальный строй, прошла целая эпоха.
Слайд 14Пифагоров строй
МУЗЫКАЛЬНЫЙ СТРОЙ, система отношений звуков по высоте. Тот или
иной музыкальный строй характеризуется рядом чисел, каждое из которых показывает
отношение частот колебаний верхних и нижних звуков интервала. Для одноголосной музыки ряда европейских народов типичен Пифагоров строй, в котором в качестве основы используется чистая квинта с отношением частот 3:2. Примерно с 16 в. в многоголосной музыке распространился т. н. чистый строй. В нем, кроме квинты, основанием служит большая терция (5:4). К началу 18 века утвердился равномерно-темперированный строй, в котором чистая октава (2:1) поделена на 12 равных полутонов ( Темперация).Слайд 15Простой математический анализ многих музыкальных шедевров позволяет совершенно иными глазами
взглянуть на них, увидеть их скрытую внутреннюю математическую красоту, которую
мы только ощущаем, слушая произведение.При взгляде на математические схемы музыкальных произведений… невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества.
Розенов
Слайд 16Иоган Себастьян Бах
Мы находим в произведениях Баха детальную и органическую
сплочённость. Закон золотого деления проявляется в них с поразительной точностью
в соотношениях крупных и мелких частей, как в строгих, так и в свободных формах, что несомненно соответствует характеру этого гениального композитора.Хроматическая фантазия