Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МБОУ СОШ №2 г. Суворова
Содержание
- 1. МБОУ СОШ №2 г. Суворова
- 2. Основные понятия теории вероятностейСлучайным называется событие, которое
- 3. ПримерБросается игральный кубик, какова вероятностьтого, что выпадет число 4.
- 4. ПримерБросается игральный кубик, какова вероятностьтого, что выпадет
- 5. ЗадачаНа тарелке 20 пирожков: 2 с мясом,
- 6. Задача На тарелке 20 пирожков: 2 с
- 7. Задачи1. Определите вероятность того, что при бросании
- 8. Ответы1. Определите вероятность того, что при бросании
- 9. Сложение вероятностейСуммой событий A и B называют
- 10. Сложение вероятностейСуммой событий A и B называют
- 11. ЗадачаВ магазине канцтоваров продается 120 ручек, из
- 12. ЗадачаВ магазине канцтоваров продается 120 ручек, из
- 13. Произведением событий A и B называется событие
- 14. Произведение вероятностейПроизведением событий A и B называется
- 15. Задача Игральную кость бросают два раза. Найдите вероятность того, что оба раза выпало число, большее 3.
- 16. ЗадачаИгральную кость бросают два раза. Найдите вероятность
- 17. ЗадачаЕсли гроссмейстер А играет белыми, то он
- 18. ЗадачаЕсли гроссмейстер А играет белыми, то он
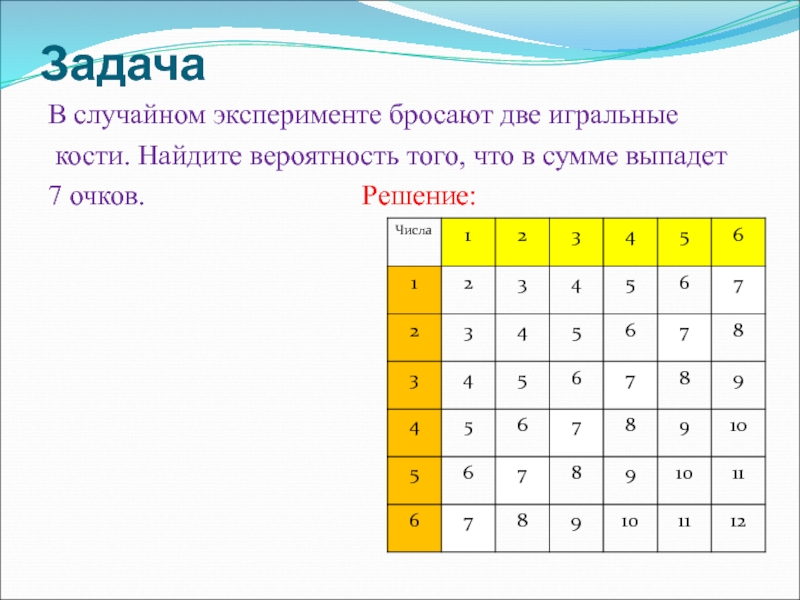
- 19. ЗадачаВ случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.
- 20. ЗадачаВ случайном эксперименте бросают две игральные кости.
- 21. ЗадачаВ случайном эксперименте бросают две игральные кости.
- 22. ЗадачаВ случайном эксперименте бросают две игральные кости.
- 23. Задачи1. Игральный кубик бросают дважды. Найдите вероятность
- 24. Задачи1. Игральный кубик бросают дважды. Найдите вероятность
- 25. ЗадачаВ случайном эксперименте симметричную монету бросают три
- 26. ЗадачаВ случайном эксперименте симметричную монету бросают три
- 27. ЗадачаВ случайном эксперименте симметричную монету бросают три
- 28. ЗадачаВ случайном эксперименте симметричную монету бросают три
- 29. Задачи1. Монету бросают три раза. Какова вероятность
- 30. Задачи1. Монету бросают три раза. Какова вероятность
- 31. Скачать презентанцию
Основные понятия теории вероятностейСлучайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.Испытанием называют такое действие, которое может привести к одному из нескольких результатов. Если n- число всех исходов
Слайды и текст этой презентации
Слайд 1МБОУ «СОШ №2 г. Суворова»
ОГЭ. Решение задач по теории вероятностей
Учитель:
Орлова Ольга Ивановна
Слайд 2Основные понятия теории вероятностей
Случайным называется событие, которое нельзя точно предсказать
заранее. Оно может либо произойти, либо нет.
Испытанием называют такое действие,
которое может привести к одному из нескольких результатов. Если n- число всех исходов некоторого испытания,
m- число благоприятствующих событию A исходов,
Вероятность события A равна P(A) =
Слайд 4Пример
Бросается игральный кубик, какова вероятность
того, что выпадет число 4.
Решение:
У кубика 6 сторон, выпасть может любая из них
⇒ число всех исходов равно n = 6.Число 4 может выпасть только в одном случае ⇒ число благоприятствующих исходов равно m = 1.
Тогда P(A)= 1 : 6
Ответ: 1/6. P(A) =
Слайд 5Задача
На тарелке 20 пирожков: 2 с мясом, 16 с капустой
и
2 с вишней. Рома наугад выбирает один пирожок.
Найдите
вероятность того, что он окажется с вишней.
Слайд 6Задача
На тарелке 20 пирожков: 2 с мясом, 16 с
капустой и
2 с вишней. Рома наугад выбирает один пирожок.
Найдите вероятность того, что он окажется
с вишней.
Решение:
Число всех исходов равно n = 20.
Число благоприятствующих исходов равно m = 2.
Тогда P(A) = 2 : 20
Ответ: 0,1.
P(A) =
Слайд 7Задачи
1. Определите вероятность того, что при бросании
игрального кубика выпадет
менее 4 очков.
2. В лыжных гонках участвуют 11 спортсменов из
России , 6 спортсменов из Норвегии и 3 спортсменаиз Швеции. Порядок, в котором спортсмены
стартуют, определяется жребием. Найдите
вероятность того, что первым будет стартовать
спортсмен из России.
3. Из 600 клавиатур для компьютера в среднем 12
неисправны. Какова вероятность, что случайно
выбранная клавиатура исправна?
Слайд 8Ответы
1. Определите вероятность того, что при бросании
игрального кубика выпадет
менее 4 очков. (0,5)
2. В лыжных гонках участвуют 11 спортсменов
изРоссии , 6 спортсменов из Норвегии и 3 спортсмена
из Швеции. Порядок, в котором спортсмены
стартуют, определяется жребием. Найдите
вероятность того, что первым будет стартовать
спортсмен из России. (0,55)
3. Из 600 клавиатур для компьютера в среднем 12
неисправны. Какова вероятность, что случайно
выбранная клавиатура исправна? (0,98)
Слайд 9Сложение вероятностей
Суммой событий A и B называют событие (A+B) ,
состоящее
в появлении либо только события A, либо только события
B,либо и события A и события B одновременно.
P(A+B) = P(A) + P(B)
Слайд 10Сложение вероятностей
Суммой событий A и B называют событие (A+B) ,
состоящее
в появлении либо только события A, либо только события
B,либо и события A и события B одновременно.
P(A+B) = P(A) + P(B)
Пример
В ящике лежат 10 шаров: 4 красных, 1 синий и 5 черных. Наугад вынимается один шар. Какова вероятность того, что шар красный или синий.
Решение:
Пусть событие A - вынут красный шар. P(A)=4:10=0,4
событие B - вынут синий шар. P(B)=1:10=0,1
Тогда вероятность того, что вынутый шар красный или синий равна P(A+B) = 0,4 + 0,1 = 0,5.
Ответ: 0,5
Слайд 11Задача
В магазине канцтоваров продается 120 ручек, из них 15 –
красных, 22 – зеленых, 27 – фиолетовых, еще есть синие
и черные, их поровну. Найдите вероятность того, что Алиса наугад вытащит синюю или зеленую ручку.
Слайд 12Задача
В магазине канцтоваров продается 120 ручек, из них 15 –
красных, 22 – зеленых, 27 – фиолетовых, еще есть синие
и черные, их поровну. Найдите вероятность того, что Алиса наугад вытащит синюю или зеленую ручку.
Решение:
Синих ручек (120 - 15 - 22 - 27) : 2 = 28
Событие A – вытащит синюю ручку. P(A) = 28 : 120 = 14/60.
Событие B – вытащит зеленую ручку. P(B) = 22 : 120 =11/60.
Тогда вероятность того, что Алиса вытащит синюю или
зеленую ручку равна P(A+B) = 14/60 + 11/60 = 5/12.
Ответ: 5/12.
Слайд 13Произведением событий A и B называется событие (AB), состоящее в
появлении и события A, и события B.
P(AB) = P(A) P(B)Произведение вероятностей
Слайд 14Произведение вероятностей
Произведением событий A и B называется событие (AB), состоящее
в появлении и события A и события B.
P(AB) = P(A) P(B)Пример
Дважды бросается игральный кубик. Какова вероятность того, что оба раза выпадет число 5.
Решение:
Пусть событие A - 1-й раз выпадет 5; P(A)=1:6
событие B - 2-й раз выпадет 5. P(B)=1:6
Тогда вероятность того, что оба раза выпадет число 5
P(AB)=1/6 1/6=1/36.
Ответ: 1/36.
Слайд 15Задача
Игральную кость бросают два раза. Найдите
вероятность того, что
оба раза выпало число,
большее 3.
Слайд 16Задача
Игральную кость бросают два раза. Найдите
вероятность того, что оба
раза выпало число,
большее 3.
Решение:
P(A) =3:6 = 0,5.
P(A) = 3:6
= 0,5.P(AB) = 0,5 0,5 = 0,25.
Ответ: 0,25
P(AB) = P(A) P(B)
Слайд 17Задача
Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера
Б с вероятностью 0,6. Если А играет черными, то А
выигрывает у Б с вероятностью 0,4. Гроссмейстеры А и Б играют 2 партии, причем во 2-ой партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза.Слайд 18Задача
Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера
Б с вероятностью 0,6. Если А играет черными, то А
выигрывает у Б с вероятностью 0,4. Гроссмейстеры А и Б играют 2 партии, причем во 2-ой партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза.Решение:
Пусть
Событие А - это выигрыш А в 1-ой партии, P(А) = 0,6.
Событие В - выигрыш А в 2-ой партии, P(В) = 0,4.
Событие C - А выиграет обе партии.
Р(C) = P(А) P(В), т.е наступят события А и В
P(C)=0,6 0,4=0,24
Ответ: 0,24
Слайд 19Задача
В случайном эксперименте бросают две игральные
кости. Найдите вероятность того,
что в сумме выпадет
7 очков.
Слайд 20Задача
В случайном эксперименте бросают две игральные
кости. Найдите вероятность того,
что в сумме выпадет
7 очков.
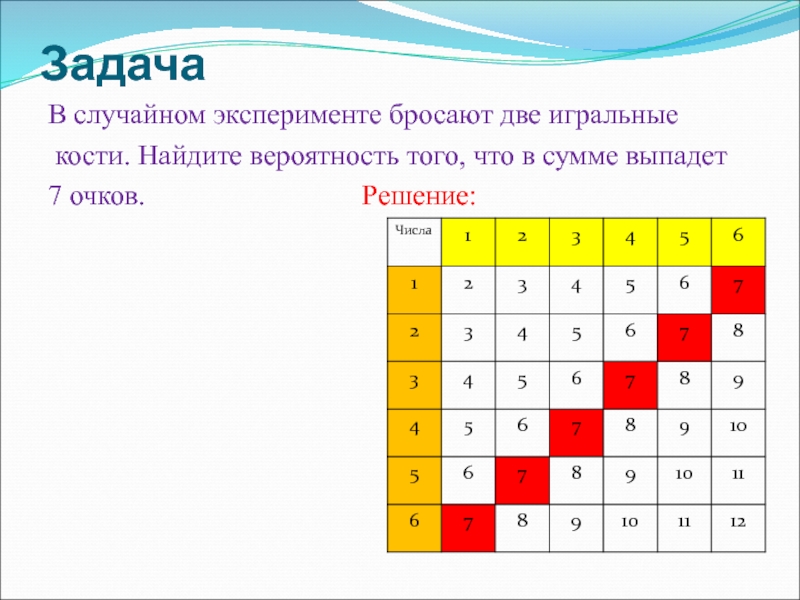
Решение:Слайд 21Задача
В случайном эксперименте бросают две игральные
кости. Найдите вероятность того,
что в сумме выпадет
7 очков.
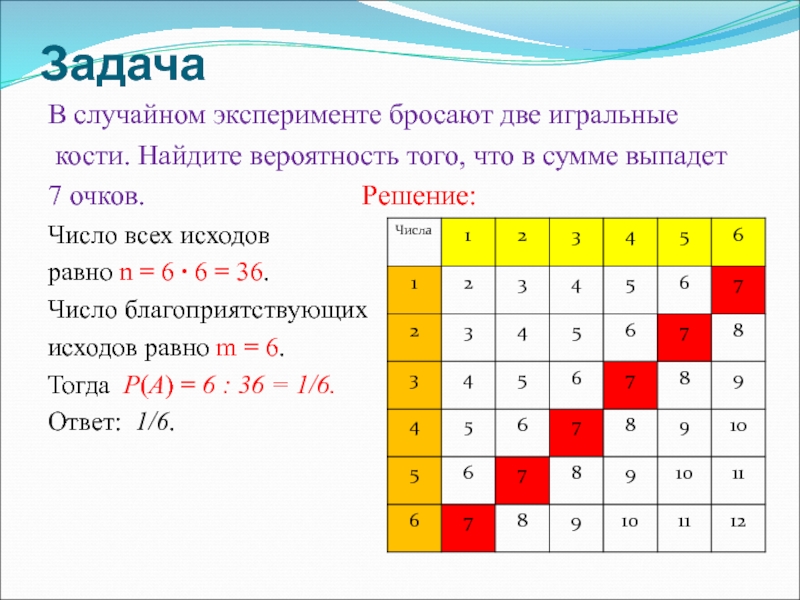
Решение:Слайд 22Задача
В случайном эксперименте бросают две игральные
кости. Найдите вероятность того,
что в сумме выпадет
7 очков.
Решение:Число всех исходов
равно n = 6 6 = 36.
Число благоприятствующих
исходов равно m = 6.
Тогда P(A) = 6 : 36 = 1/6.
Ответ: 1/6.
Слайд 23Задачи
1. Игральный кубик бросают дважды. Найдите
вероятность того, что первый
раз выпадет число 6.
2. Игральный кубик бросают дважды. Найдите вероятность
того, что первый раз и во второй раз выпадет одинаковое число очков.3. Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна?
Слайд 24Задачи
1. Игральный кубик бросают дважды. Найдите
вероятность того, что первый
раз выпадет число 6. (1/6)
2. Игральный кубик бросают дважды. Найдите
вероятность того, что первый раз и во второй раз выпадет одинаковое число очков. (1/6)3. Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна? (7)
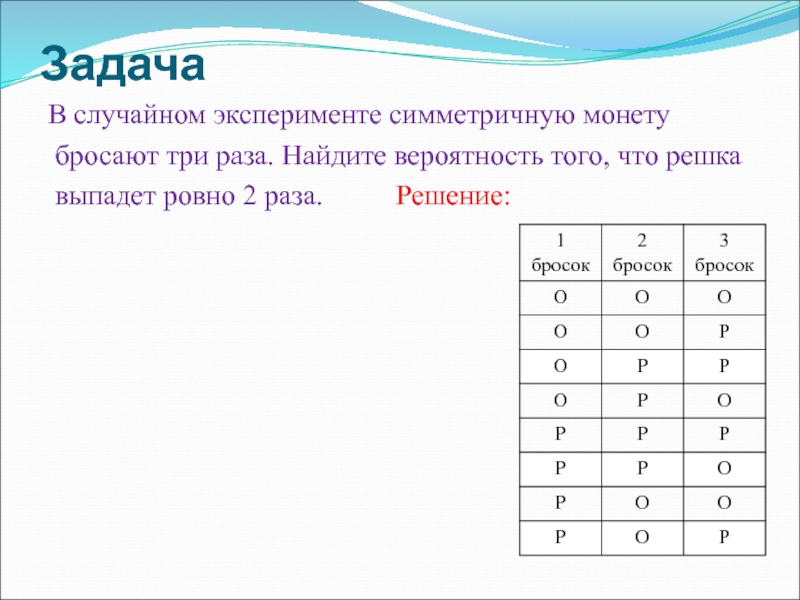
Слайд 25Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность
того, что решка
выпадет ровно 2 раза.
Слайд 26Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность
того, что решка
выпадет ровно 2 раза.
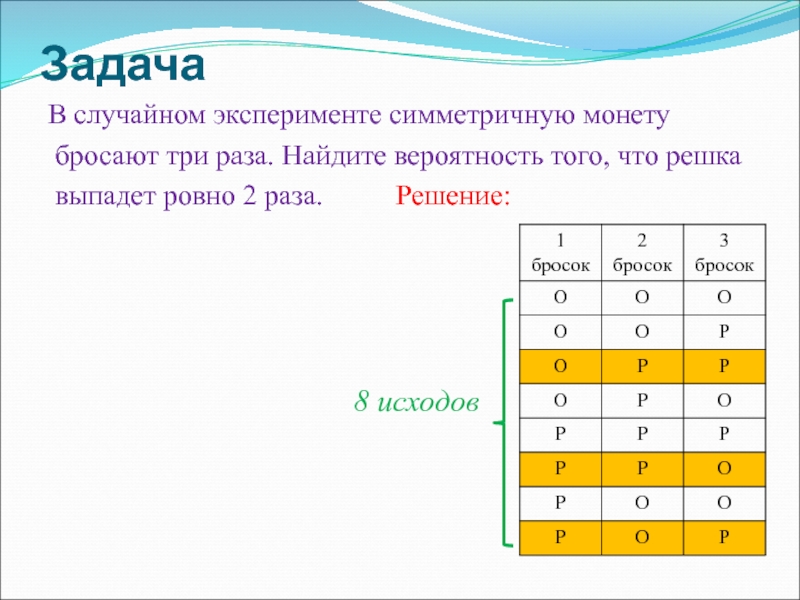
Решение:Слайд 27Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность
того, что решка
выпадет ровно 2 раза.
Решение:8 исходов
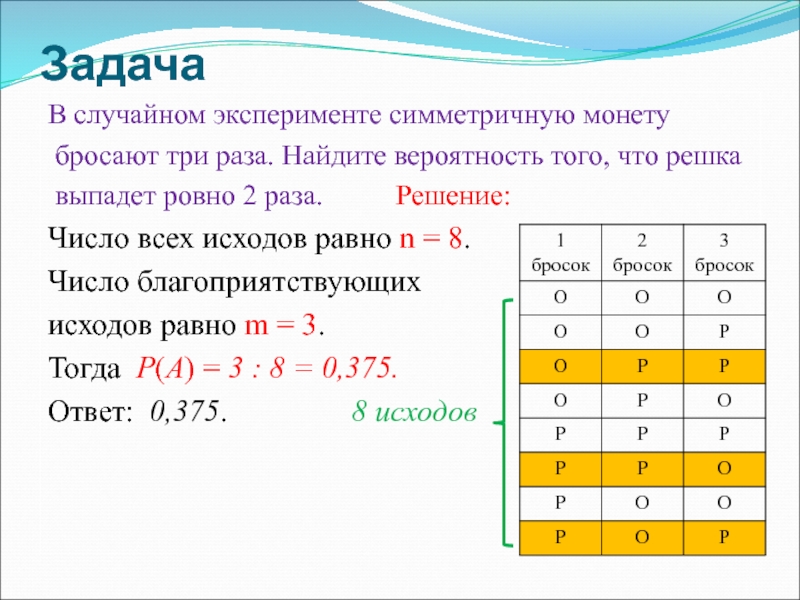
Слайд 28Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность
того, что решка
выпадет ровно 2 раза.
Решение:Число всех исходов равно n = 8.
Число благоприятствующих
исходов равно m = 3.
Тогда P(A) = 3 : 8 = 0,375.
Ответ: 0,375. 8 исходов
Слайд 29Задачи
1. Монету бросают три раза. Какова вероятность того, что результаты
двух первых бросков будут одинаковы?
2. Монету бросают три раза.
Найдите вероятность того, что результаты первого и последнего броска различны. 3. В случайном эксперименте симметричную монету
бросают два раза. Найдите вероятность того, что орел выпадет ровно один раз.
Слайд 30Задачи
1. Монету бросают три раза. Какова вероятность того, что результаты
двух первых бросков будут одинаковы? (0,5)
2. Монету бросают три раза.
Найдите вероятность того, что результаты первого и последнего броска различны. (0,5)3. В случайном эксперименте симметричную монету
бросают два раза. Найдите вероятность того, что орел выпадет ровно один раз. (0,5)