Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медична інформатика
Содержание
- 1. Медична інформатика
- 2. 2. ЗР випадкових величинЗакон розподілу випадкових величин
- 3. 2.1. ЗР дискретних ВВБіноміальний розподіл (розподіл Бернуллі)Біноміальному
- 4. ПрикладРозрахувати ймовірність того, що з 20 дітей,
- 5. Розподіл Пуассона ЗР дискретних ВВРозподіл Пуассона,
- 6. ПрикладВакцина формує імунітет від деякого захворювання з
- 7. Нормальний закон розподілу (Гаусса)2.2. ЗР неперервних ВВНормальному
- 8. ЗР неперервних ВВРозподіл
- 9. ЗР неперервних ВВРозподіл Ст’юдента
- 10. 2.3. Емпіричні ЗР ВВ Емпіричні закони розподілу
- 11. ЗР випадкових величинФункція розподілу – це функція
- 12. Скачать презентанцию
2. ЗР випадкових величинЗакон розподілу випадкових величин - функціональна залежність між значеннями випадкових величин та ймовірностями з якими вони приймають ці значення. Закон розподілу може бути заданий у вигляді таблиці, формули
Слайды и текст этой презентации
Слайд 1
Основи статистичних
методів обробки медико-біологічних даних
Лекція №2
з дисципліни “Медична
інформатика”
для студентів ІІ курсу
медичних факультетів
Слайд 22. ЗР випадкових величин
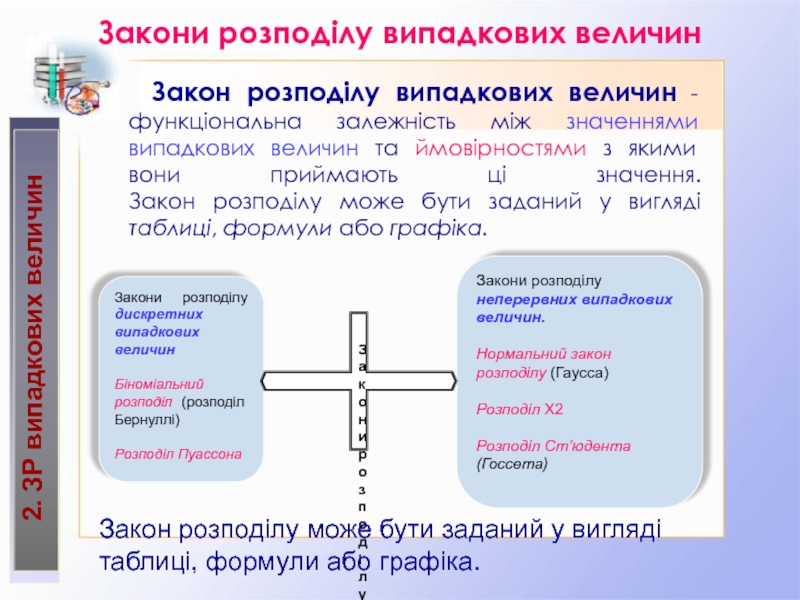
Закон розподілу випадкових величин - функціональна залежність
між значеннями випадкових величин та ймовірностями з якими вони приймають
ці значення. Закон розподілу може бути заданий у вигляді таблиці, формули або графіка.Закони розподілу випадкових величин
Закони розподілу дискретних випадкових величин
Біноміальний розподіл (розподіл Бернуллі)
Розподіл Пуассона
Закони розподілу неперервних випадкових величин.
Нормальний закон розподілу (Гаусса)
Розподіл Х2
Розподіл Ст’юдента (Госсета)
Закони розподілу випадкових величин
Закон розподілу може бути заданий у вигляді таблиці, формули або графіка.
Слайд 3
2.1. ЗР дискретних ВВ
Біноміальний розподіл (розподіл Бернуллі)
Біноміальному закону розподілу підпорядковуються
випадкові події такі, як число викликів швидкої допомоги за певний
проміжок часу, черги до лікаря в поліклініці, епідемії тощо
Слайд 4Приклад
Розрахувати ймовірність того, що з 20 дітей, які народяться, рівно
11 дітей будуть дівчатами
n=20, m=11, p=0.5
Excel: ф-я БИНОМРАСП (m; n;
p)
Слайд 5Розподіл Пуассона
ЗР дискретних ВВ
Розподіл Пуассона, як граничний біноміальний використовується
при вирішенні задач надійності медичного обладнання та апаратури, розповсюдження епідемії,
викликів до хворого дільничих лікарів та в інших задачах масового обслуговування.
Слайд 6Приклад
Вакцина формує імунітет від деякого захворювання з ймовірністю 0,999. Провакциновано
4000 мешканців міста. Яка ймовірність того, що двоє з них
не набули імунітету. ЗР дискретних ВВ
Excel: ф-я ПУАССОН (m; л) (2; 4)
Відповідь: ПУАССОН (2;4)= 0,147, отже, ймовірність того що двоє пацієнтів не набудуть імунітету становить 0,147
Слайд 7Нормальний закон розподілу (Гаусса)
2.2. ЗР неперервних ВВ
Нормальному закону розподілу підпорядковуються
такі випадкові величини як частота дихання, частота серцевих скорочень, динаміка
росту популяції тощо.
Слайд 102.3. Емпіричні ЗР ВВ
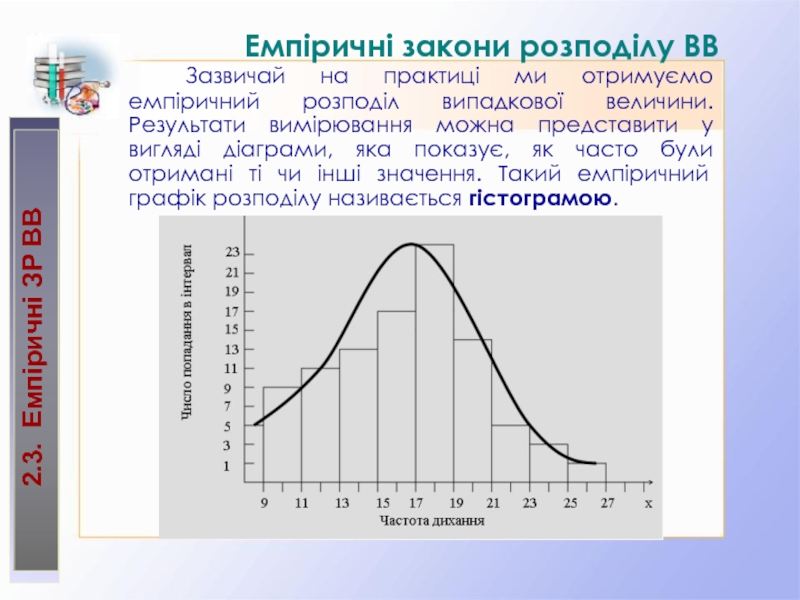
Емпіричні закони розподілу ВВ
Зазвичай на
практиці ми отримуємо емпіричний розподіл випадкової величини. Результати вимірювання можна
представити у вигляді діаграми, яка показує, як часто були отримані ті чи інші значення. Такий емпіричний графік розподілу називається гістограмою.
Слайд 11ЗР випадкових величин
Функція розподілу – це функція F(x), котра задає
ймовірність того, що випадкова величина Х приймає у випробовуванні прийме
значення менше х:F(x)=Р(Х<х).
Її називають інтегральною функцією.
Функція розподілу неперервної випадкової величини F(x) є неспадною неперервною функцією. Для дискретних випадкових величин функція розподілу є розривною ступеневою функцією.
Щільність розподілу для неперервної випадкової величини – це похідна від функції розподілу
Параметри розподілу: математичне сподівання, дисперсія.
ЗР випадкових величин
