Механические колебания

периодически изменяющихся сил.     При наличии таких сил колебания называют вынужденными.

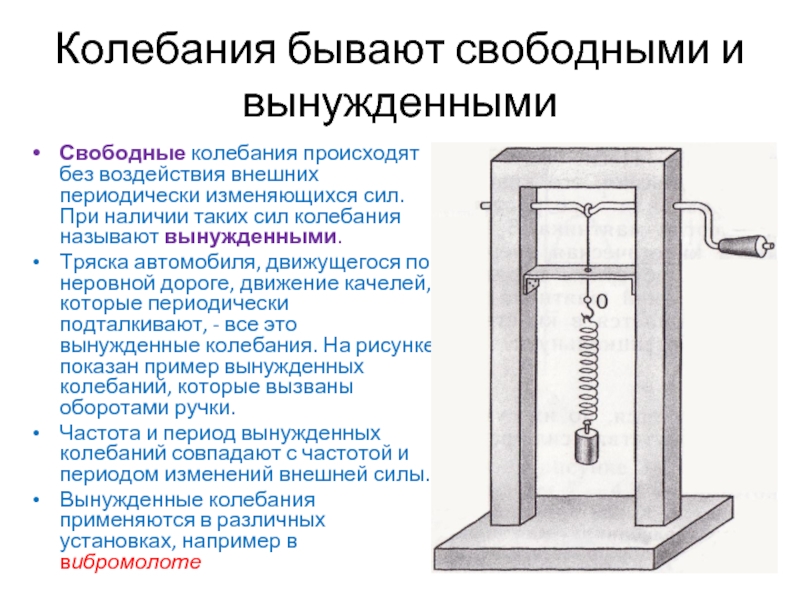
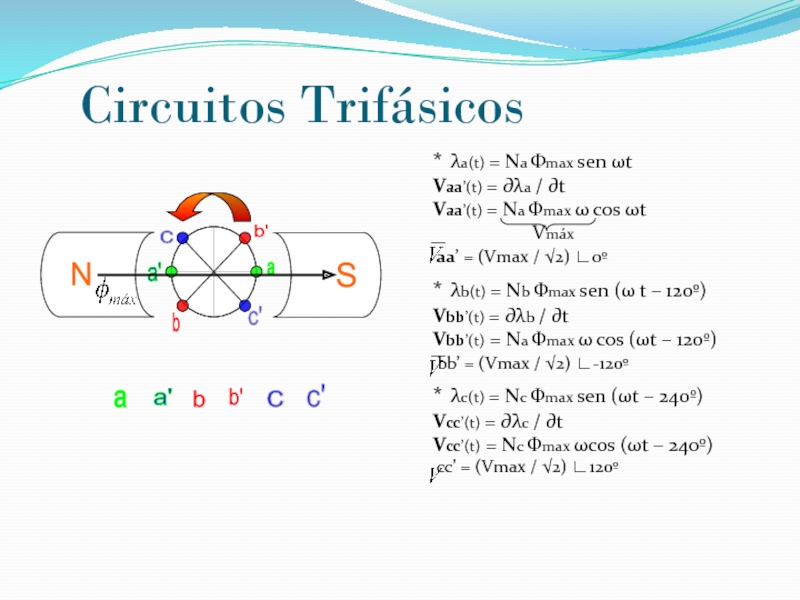
Тряска автомобиля, движущегося по неровной дороге, движение качелей, которые периодически подталкивают, - все это вынужденные колебания. На рисунке показан пример вынужденных колебаний, которые вызваны оборотами ручки.
Частота и период вынужденных колебаний совпадают с частотой и периодом изменений внешней силы.
Вынужденные колебания применяются в различных установках, например в вибромолоте

на ветру, качание маятника в настенных часах, волны на воде.

Рассмотрим колебательное движение на примере двух маятников.

Нитяной маятник представляет собой шарик, прикрепленный к тонкой, легкой нити. Если шарик сместить в сторону, и отпустить, то он периодически начнет колебаться.

Пружинный маятник представляет собой груз, способный колебаться под действием силы упругости пружины.

необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была

пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
F (t) = ma (t) = –m ω2 x (t).

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Fупр = –kx.
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.
Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.

колебаний груза на пружине равен

Величина χ аналогична жесткости пружины k. Второй закон Ньютона для

вращательного движения диска записывается в виде


где I = IC – момент инерции диска относительно оси, проходящий через центр масс, ε – угловое ускорение.
По аналогии с грузом на пружине можно получить:
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.

маятника.
Следовательно,

момент инерции маятника относительно оси вращения O. Модуль коэффициента пропорциональности

между ускорением и смещением равен квадрату круговой частоты:

Здесь ω0 – собственная частота малых колебаний физического маятника.